- Research Article
- Open access
- Published:
Volterra-Type Operators on Zygmund Spaces
Journal of Inequalities and Applications volume 2007, Article number: 032124 (2007)
Abstract
The boundedness and the compactness of the two integral operators ;
; , where
, where is an analytic function on the open unit disk in the complex plane, on the Zygmund space are studied.
is an analytic function on the open unit disk in the complex plane, on the Zygmund space are studied.
References
Duren PL: Theory of Hp Spaces, Pure and Applied Mathematics. Volume 38. Academic Press, New York, NY, USA; 1970:xii+258.
Pommerenke Ch: Schlichte Funktionen und analytische Funktionen von beschränkter mittlerer Oszillation. Commentarii Mathematici Helvetici 1977,52(4):591–602.
Aleman A, Siskakis AG: An integral operator on
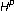 . Complex Variables. Theory and Application 1995,28(2):149–158. 10.1080/17476939508814844
. Complex Variables. Theory and Application 1995,28(2):149–158. 10.1080/17476939508814844Aleman A, Siskakis AG: Integration operators on Bergman spaces. Indiana University Mathematics Journal 1997,46(2):337–356.
Aleman A, Cima JA: An integral operator on
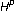 and Hardy's inequality. Journal d'Analyse Mathématique 2001, 85: 157–176.
and Hardy's inequality. Journal d'Analyse Mathématique 2001, 85: 157–176.Benke G, Chang D-C: A note on weighted Bergman spaces and the Cesàro operator. Nagoya Mathematical Journal 2000, 159: 25–43.
Chang D-C, Gilbert R, Tie J: Bergman projection and weighted holomorphic functions. In Reproducing Kernel Spaces and Applications, Oper. Theory Adv. Appl.. Volume 143. Birkhäuser, Basel, Switzerland; 2003:147–169.
Chang D-C, Stević S: The generalized Cesàro operator on the unit polydisk. Taiwanese Journal of Mathematics 2003,7(2):293–308.
Hu Z: Extended Cesàro operators on mixed norm spaces. Proceedings of the American Mathematical Society 2003,131(7):2171–2179. 10.1090/S0002-9939-02-06777-1
Hu Z: Extended Cesáro operators on the Bloch space in the unit ball of
 . Acta Mathematica Scientia. Series B. English Edition 2003,23(4):561–566.
. Acta Mathematica Scientia. Series B. English Edition 2003,23(4):561–566.Li S: Riemann-Stieltjes operators from
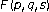 spaces to
spaces to -Bloch spaces on the unit ball. Journal of Inequalities and Applications 2006, 2006: 14 pages.
-Bloch spaces on the unit ball. Journal of Inequalities and Applications 2006, 2006: 14 pages.Li S, Stević S: Reimann-Stieltjies type integral operators on the unit ball in
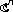 . Complex Variables Elliptic Functions 2007., 2:
. Complex Variables Elliptic Functions 2007., 2:Siskakis AG, Zhao R: A Volterra type operator on spaces of analytic functions. In Function Spaces (Edwardsville, IL, 1998), Contemp. Math.. Volume 232. American Mathematical Society, Providence, RI, USA; 1999:299–311.
Stević S: Cesàro averaging operators. Mathematische Nachrichten 2003,248/249(1):185–189. 10.1002/mana.200310013
Stević S: On an integral operator on the unit ball in
 . Journal of Inequalities and Applications 2005,2005(1):81–88. 10.1155/JIA.2005.81
. Journal of Inequalities and Applications 2005,2005(1):81–88. 10.1155/JIA.2005.81Stević S: Boundedness and compactness of an integral operator on a weighted space on the polydisc. Indian Journal of Pure and Applied Mathematics 2006,37(6):343–355.
Tamrazov PM: Contour and solid structure properties of holomorphic functions of a complex variable. Russian Mathematical Surveys 1973,28(1):141–1731. 10.1070/RM1973v028n01ABEH001398
Cowen CC, MacCluer BD: Composition Operators on Spaces of Analytic Functions, Studies in Advanced Mathematics. CRC Press, Boca Raton, Fla, USA; 1995:xii+388.
Madigan K, Matheson A: Compact composition operators on the Bloch space. Transactions of the American Mathematical Society 1995,347(7):2679–2687. 10.2307/2154848
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, S., Stević, S. Volterra-Type Operators on Zygmund Spaces. J Inequal Appl 2007, 032124 (2007). https://doi.org/10.1155/2007/32124
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/32124
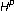 . Complex Variables. Theory and Application 1995,28(2):149–158. 10.1080/17476939508814844
. Complex Variables. Theory and Application 1995,28(2):149–158. 10.1080/17476939508814844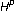 and Hardy's inequality. Journal d'Analyse Mathématique 2001, 85: 157–176.
and Hardy's inequality. Journal d'Analyse Mathématique 2001, 85: 157–176. . Acta Mathematica Scientia. Series B. English Edition 2003,23(4):561–566.
. Acta Mathematica Scientia. Series B. English Edition 2003,23(4):561–566.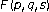 spaces to
spaces to -Bloch spaces on the unit ball. Journal of Inequalities and Applications 2006, 2006: 14 pages.
-Bloch spaces on the unit ball. Journal of Inequalities and Applications 2006, 2006: 14 pages. . Complex Variables Elliptic Functions 2007., 2:
. Complex Variables Elliptic Functions 2007., 2: . Journal of Inequalities and Applications 2005,2005(1):81–88. 10.1155/JIA.2005.81
. Journal of Inequalities and Applications 2005,2005(1):81–88. 10.1155/JIA.2005.81