- Research Article
- Open access
- Published:
Perturbed Iterative Algorithms for Generalized Nonlinear Set-Valued Quasivariational Inclusions Involving Generalized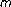 -Accretive Mappings
-Accretive Mappings
Journal of Inequalities and Applications volume 2007, Article number: 029863 (2007)
Abstract
A new class of generalized nonlinear set-valued quasivariational inclusions involving generalized -accretive mappings in Banach spaces are studied, which included many variational inclusions studied by others in recent years. By using the properties of the resolvent operator associated with generalized
-accretive mappings in Banach spaces are studied, which included many variational inclusions studied by others in recent years. By using the properties of the resolvent operator associated with generalized -accretive mappings, we established the equivalence between the generalized nonlinear set-valued quasi-variational inclusions and the fixed point problems, and some new perturbed iterative algorithms, proved that its proximate solution converges strongly to its exact solution in real Banach spaces.
-accretive mappings, we established the equivalence between the generalized nonlinear set-valued quasi-variational inclusions and the fixed point problems, and some new perturbed iterative algorithms, proved that its proximate solution converges strongly to its exact solution in real Banach spaces.
References
Hassouni A, Moudafi A: A perturbed algorithm for variational inclusions. Journal of Mathematical Analysis and Applications 1994,185(3):706–712. 10.1006/jmaa.1994.1277
Adly S: Perturbed algorithms and sensitivity analysis for a general class of variational inclusions. Journal of Mathematical Analysis and Applications 1996,201(2):609–630. 10.1006/jmaa.1996.0277
Ding XP: Perturbed proximal point algorithms for generalized quasivariational inclusions. Journal of Mathematical Analysis and Applications 1997,210(1):88–101. 10.1006/jmaa.1997.5370
Ding XP, Luo CL: Perturbed proximal point algorithms for general quasi-variational-like inclusions. Journal of Computational and Applied Mathematics 2000,113(1–2):153–165. 10.1016/S0377-0427(99)00250-2
Huang N-J: On the generalized implicit quasivariational inequalities. Journal of Mathematical Analysis and Applications 1997,216(1):197–210. 10.1006/jmaa.1997.5671
Huang N-J: A new completely general class of variational inclusions with noncompact valued mappings. Computers & Mathematics with Applications 1998,35(10):9–14. 10.1016/S0898-1221(98)00067-4
Huang N-J, Bai M-R, Cho YJ, Kang SM: Generalized nonlinear mixed quasi-variational inequalities. Computers & Mathematics with Applications 2000,40(2–3):205–215. 10.1016/S0898-1221(00)00154-1
Ahmad R, Ansari QH: An iterative algorithm for generalized nonlinear variational inclusions. Applied Mathematics Letters 2000,13(5):23–26. 10.1016/S0893-9659(00)00028-8
Ahmad R, Siddiqi AH, Khan Z: Proximal point algorithm for generalized multivalued nonlinear quasi-variational-like inclusions in Banach spaces. Applied Mathematics and Computation 2005,163(1):295–308. 10.1016/j.amc.2004.02.021
Chang SS, Cho YJ, Lee BS, Jung IH: Generalized set-valued variational inclusions in Banach spaces. Journal of Mathematical Analysis and Applications 2000,246(2):409–422. 10.1006/jmaa.2000.6795
Chidume CE, Kazmi KR, Zegeye H: Iterative approximation of a solution of a general variational-like inclusion in Banach spaces. International Journal of Mathematics and Mathematical Sciences 2004,2004(22):1159–1168. 10.1155/S0161171204209395
Fang Y-P, Huang N-J:
 -accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7
-accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7He X: On
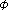 -strongly accretive mappings and some set-valued variational problems. Journal of Mathematical Analysis and Applications 2003,277(2):504–511. 10.1016/S0022-247X(02)00582-6
-strongly accretive mappings and some set-valued variational problems. Journal of Mathematical Analysis and Applications 2003,277(2):504–511. 10.1016/S0022-247X(02)00582-6Huang N-J: Nonlinear implicit quasi-variational inclusions involving generalized
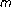 -accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425.
-accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425.Huang N-J, Fang Y-P: Generalized
 -accretive mappings in Banach spaces. Journal of Sichuan University 2001,38(4):591–592.
-accretive mappings in Banach spaces. Journal of Sichuan University 2001,38(4):591–592.Huang N-J, Fang Y-P: A new class of general variational inclusions involving maximal
 -monotone mappings. Publicationes Mathematicae Debrecen 2003,62(1–2):83–98.
-monotone mappings. Publicationes Mathematicae Debrecen 2003,62(1–2):83–98.Huang N-J, Fang Y-P: Iterative processes with errors for nonlinear set-valued variational inclusions involving accretive type mappings. Computers & Mathematics with Applications 2004,47(4–5):727–738. 10.1016/S0898-1221(04)90060-0
Huang N-J, Fang Y-P, Cho YJ: Generalized
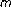 -accretive mappings and variational inclusions in Banach spaces. Journal of Concrete and Applicable Mathematics 2005,3(1):31–40.
-accretive mappings and variational inclusions in Banach spaces. Journal of Concrete and Applicable Mathematics 2005,3(1):31–40.Huang N-J, Fang Y-P, Deng CX: A new class of generalized nonlinear variational inclusions in Banach spaces. In Proceedings of International Conference on Mathematical Programming, 2004, Shanghai, China. Edited by: Yue MY, Han JY, Zhang LS, Zhang SZ. Shanghai University Press; 207–214.
Jin M-M: A new proximal point algorithm with errors for nonlinear variational inclusions involving generalized
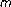 -accretive mappings. Nonlinear Analysis Forum 2004,9(1):87–96.
-accretive mappings. Nonlinear Analysis Forum 2004,9(1):87–96.Jin M-M, Liu Q-K: Nonlinear quasi-variational inclusions involving generalized
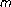 -accretive mappings. Nonlinear Functional Analysis and Applications 2004,9(3):485–494.
-accretive mappings. Nonlinear Functional Analysis and Applications 2004,9(3):485–494.Jin M-M: Generalized nonlinear implicit quasivariational inclusions with relaxed monotone mappings. Advances in Nonlinear Variational Inequalities 2004,7(2):173–181.
Kazmi KR: Mann and Ishikawa type perturbed iterative algorithms for generalized quasivariational inclusions. Journal of Mathematical Analysis and Applications 1997,209(2):572–584. 10.1006/jmaa.1997.5368
Liu L-W, Li Y-Q: On generalized set-valued variational inclusions. Journal of Mathematical Analysis and Applications 2001,261(1):231–240. 10.1006/jmaa.2001.7493
Verma RU: Generalized variational inequalities involving multivalued relaxed monotone operators. Applied Mathematics Letters 1997,10(4):107–109. 10.1016/S0893-9659(97)00068-2
Verma RU:
 -monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(2):193–195. 10.1155/S1048953304403013
-monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(2):193–195. 10.1155/S1048953304403013Verma RU: Approximation-solvability of a class of
 -monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004,8(1):55–66.
-monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004,8(1):55–66.Yuan XZ: KKM Theory and Applications in Nonlinear Analysis. Marcel Dekker, New York, NY, USA; 1999.
Petryshyn WV: A characterization of strict convexity of Banach spaces and other uses of duality mappings. Journal of Functional Analysis 1970, 6: 282–291. 10.1016/0022-1236(70)90061-3
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969,30(2):475–488.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jin, MM. Perturbed Iterative Algorithms for Generalized Nonlinear Set-Valued Quasivariational Inclusions Involving Generalized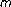 -Accretive Mappings.
J Inequal Appl 2007, 029863 (2007). https://doi.org/10.1155/2007/29863
-Accretive Mappings.
J Inequal Appl 2007, 029863 (2007). https://doi.org/10.1155/2007/29863
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/29863
 -accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7
-accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7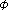 -strongly accretive mappings and some set-valued variational problems. Journal of Mathematical Analysis and Applications 2003,277(2):504–511. 10.1016/S0022-247X(02)00582-6
-strongly accretive mappings and some set-valued variational problems. Journal of Mathematical Analysis and Applications 2003,277(2):504–511. 10.1016/S0022-247X(02)00582-6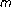 -accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425.
-accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425. -accretive mappings in Banach spaces. Journal of Sichuan University 2001,38(4):591–592.
-accretive mappings in Banach spaces. Journal of Sichuan University 2001,38(4):591–592. -monotone mappings. Publicationes Mathematicae Debrecen 2003,62(1–2):83–98.
-monotone mappings. Publicationes Mathematicae Debrecen 2003,62(1–2):83–98.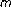 -accretive mappings and variational inclusions in Banach spaces. Journal of Concrete and Applicable Mathematics 2005,3(1):31–40.
-accretive mappings and variational inclusions in Banach spaces. Journal of Concrete and Applicable Mathematics 2005,3(1):31–40.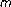 -accretive mappings. Nonlinear Analysis Forum 2004,9(1):87–96.
-accretive mappings. Nonlinear Analysis Forum 2004,9(1):87–96.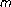 -accretive mappings. Nonlinear Functional Analysis and Applications 2004,9(3):485–494.
-accretive mappings. Nonlinear Functional Analysis and Applications 2004,9(3):485–494. -monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(2):193–195. 10.1155/S1048953304403013
-monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(2):193–195. 10.1155/S1048953304403013 -monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004,8(1):55–66.
-monotone variational inclusion problems. Journal of the Korean Society for Industrial and Applied Mathematics 2004,8(1):55–66.