- Research Article
- Open access
- Published:
Spectrum of Class Operators
Operators
Journal of Inequalities and Applications volume 2007, Article number: 027195 (2007)
Abstract
This paper discusses some spectral properties of class operators for
operators for ,
, ,
, , and
, and . It is shown that if
. It is shown that if is a class
is a class operator, then the Riesz idempotent
operator, then the Riesz idempotent of
of with respect to each nonzero isolated point spectrum
with respect to each nonzero isolated point spectrum is selfadjoint and
is selfadjoint and . Afterwards, we prove that every class
. Afterwards, we prove that every class operator has SVEP and property
operator has SVEP and property , and Weyl's theorem holds for
, and Weyl's theorem holds for when
when .
.
References
Martin M, Putinar M: Lectures on Hyponormal Operators, Operator Theory: Advances and Applications. Volume 39. Birkhäuser, Basel, Switzerland; 1989:304.
Xia D: Spectral Theory of Hyponormal Operators, Operator Theory: Advances and Applications. Volume 10. Birkhäuser, Basel, Switzerland; 1983:xiv+241.
Tanahashi K: On log-hyponormal operators. Integral Equations and Operator Theory 1999,34(3):364–372. 10.1007/BF01300584
Aluthge A, Wang D:
 -hyponormal operators. Integral Equations and Operator Theory 2000,36(1):1–10. 10.1007/BF01236285
-hyponormal operators. Integral Equations and Operator Theory 2000,36(1):1–10. 10.1007/BF01236285Fujii M, Himeji C, Matsumoto A: Theorems of Ando and Saito for
 -hyponormal operators. Mathematica Japonica 1994,39(3):595–598.
-hyponormal operators. Mathematica Japonica 1994,39(3):595–598.Aluthge A: On
 -hyponormal operators for.
-hyponormal operators for.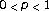 Integral Equations and Operator Theory 1990,13(3):307–315. 10.1007/BF01199886
Integral Equations and Operator Theory 1990,13(3):307–315. 10.1007/BF01199886Ito M: Some classes of operators associated with generalized Aluthge transformation. SUT Journal of Mathematics 1999,35(1):149–165.
Yang C, Yuan J: Spectrum of class
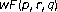 operators for
operators for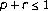 and
and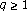 . Acta Scientiarum Mathematicarum 2005,71(3–4):767–779.
. Acta Scientiarum Mathematicarum 2005,71(3–4):767–779.Yang C, Yuan J: On class
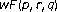 operators. Acta Mathematica Scientia. Series A. (Chinese Edition) 2007,27(5):769–780.
operators. Acta Mathematica Scientia. Series A. (Chinese Edition) 2007,27(5):769–780.Ito M, Yamazaki T: Relations between two inequalities
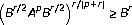 and
and and their applications. Integral Equations and Operator Theory 2002,44(4):442–450. 10.1007/BF01193670
and their applications. Integral Equations and Operator Theory 2002,44(4):442–450. 10.1007/BF01193670Fujii M, Jung D, Lee SH, Lee MY, Nakamoto R: Some classes of operators related to paranormal and log-hyponormal operators. Mathematica Japonica 2000,51(3):395–402.
Furuta T, Ito M, Yamazaki T: A subclass of paranormal operators including class of log-hyponormal and several related classes. Scientiae Mathematicae 1998,1(3):389–403.
Fujii M, Nakamoto R: Some classes of operators derived from Furuta inequality. Scientiae Mathematicae 2000,3(1):87–94.
Aluthge A, Wang D: The joint approximate point spectrum of an operator. Hokkaido Mathematical Journal 2002,31(1):187–197.
Chō M, Tanahashi K: Isolated point of spectrum of
 -hyponormal, log-hyponormal operators. Integral Equations and Operator Theory 2002,43(4):379–384. 10.1007/BF01212700
-hyponormal, log-hyponormal operators. Integral Equations and Operator Theory 2002,43(4):379–384. 10.1007/BF01212700Chō M, Yamazaki T: An operator transform from class
 to the class of hyponormal operators and its application. Integral Equations and Operator Theory 2005,53(4):497–508. 10.1007/s00020-004-1332-6
to the class of hyponormal operators and its application. Integral Equations and Operator Theory 2005,53(4):497–508. 10.1007/s00020-004-1332-6Han YM, Lee JI, Wang D: Riesz idempotent and Weyl's theorem for
 -hyponormal operators. Integral Equations and Operator Theory 2005,53(1):51–60. 10.1007/s00020-003-1313-1
-hyponormal operators. Integral Equations and Operator Theory 2005,53(1):51–60. 10.1007/s00020-003-1313-1Kimura F: Analysis of non-normal operators via Aluthge transformation. Integral Equations and Operator Theory 2004,50(3):375–384. 10.1007/s00020-003-1231-2
Tanahashi K, Uchiyama A: Isolated point of spectrum of
 -quasihyponormal operators. Linear Algebra and Its Applications 2002,341(1–3):345–350.
-quasihyponormal operators. Linear Algebra and Its Applications 2002,341(1–3):345–350.Uchiyama A: On the isolated points of the spectrum of paranormal operators. Integral Equations and Operator Theory 2006,55(1):145–151. 10.1007/s00020-005-1386-0
Uchiyama A, Tanahashi K: On the Riesz idempotent of class
 operators. Mathematical Inequalities & Applications 2002,5(2):291–298.
operators. Mathematical Inequalities & Applications 2002,5(2):291–298.Uchiyama A, Tanahashi K, Lee JI: Spectrum of class
 operators. Acta Scientiarum Mathematicarum 2004,70(1–2):279–287.
operators. Acta Scientiarum Mathematicarum 2004,70(1–2):279–287.Tanahashi K: Putnam's inequality for log-hyponormal operators. Integral Equations and Operator Theory 2004,48(1):103–114. 10.1007/s00020-999-1172-5
Stampfli JG: Hyponormal operators. Pacific Journal of Mathematics 1962,12(4):1453–1458.
Huruya T: A note on
 -hyponormal operators. Proceedings of the American Mathematical Society 1997,125(12):3617–3624. 10.1090/S0002-9939-97-04004-5
-hyponormal operators. Proceedings of the American Mathematical Society 1997,125(12):3617–3624. 10.1090/S0002-9939-97-04004-5Chō M, Itoh M: Putnam's inequality for
 -hyponormal operators. Proceedings of the American Mathematical Society 1995,123(8):2435–2440.
-hyponormal operators. Proceedings of the American Mathematical Society 1995,123(8):2435–2440.Riesz F, Sz.-Nagy B: Functional Analysis. Frederick Ungar, New York, NY, USA; 1955:xii+468.
Conway JB: A Course in Functional Analysis, Graduate Texts in Mathematics. Volume 96. 2nd edition. Springer, New York, NY, USA; 1990:xvi+399.
Finch JK: The single valued extension property on a Banach space. Pacific Journal of Mathematics 1975,58(1):61–69.
Bishop E: A duality theorem for an arbitrary operator. Pacific Journal of Mathematics 1959,9(2):379–397.
Coburn LA: Weyl's theorem for nonnormal operators. Michigan Mathematical Journal 1966,13(3):285–288.
Kim IH: On
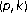 -quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.
-quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.Lee WY, Lee SH: A spectral mapping theorem for the Weyl spectrum. Glasgow Mathematical Journal 1996,38(1):61–64. 10.1017/S0017089500031268
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yuan, J., Gao, Z. Spectrum of Class Operators.
J Inequal Appl 2007, 027195 (2007). https://doi.org/10.1155/2007/27195
Operators.
J Inequal Appl 2007, 027195 (2007). https://doi.org/10.1155/2007/27195
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/27195
 -hyponormal operators. Integral Equations and Operator Theory 2000,36(1):1–10. 10.1007/BF01236285
-hyponormal operators. Integral Equations and Operator Theory 2000,36(1):1–10. 10.1007/BF01236285 -hyponormal operators. Mathematica Japonica 1994,39(3):595–598.
-hyponormal operators. Mathematica Japonica 1994,39(3):595–598. -hyponormal operators for.
-hyponormal operators for.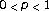 Integral Equations and Operator Theory 1990,13(3):307–315. 10.1007/BF01199886
Integral Equations and Operator Theory 1990,13(3):307–315. 10.1007/BF01199886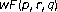 operators for
operators for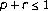 and
and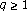 . Acta Scientiarum Mathematicarum 2005,71(3–4):767–779.
. Acta Scientiarum Mathematicarum 2005,71(3–4):767–779.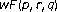 operators. Acta Mathematica Scientia. Series A. (Chinese Edition) 2007,27(5):769–780.
operators. Acta Mathematica Scientia. Series A. (Chinese Edition) 2007,27(5):769–780.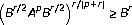 and
and and their applications. Integral Equations and Operator Theory 2002,44(4):442–450. 10.1007/BF01193670
and their applications. Integral Equations and Operator Theory 2002,44(4):442–450. 10.1007/BF01193670 -hyponormal, log-hyponormal operators. Integral Equations and Operator Theory 2002,43(4):379–384. 10.1007/BF01212700
-hyponormal, log-hyponormal operators. Integral Equations and Operator Theory 2002,43(4):379–384. 10.1007/BF01212700 to the class of hyponormal operators and its application. Integral Equations and Operator Theory 2005,53(4):497–508. 10.1007/s00020-004-1332-6
to the class of hyponormal operators and its application. Integral Equations and Operator Theory 2005,53(4):497–508. 10.1007/s00020-004-1332-6 -hyponormal operators. Integral Equations and Operator Theory 2005,53(1):51–60. 10.1007/s00020-003-1313-1
-hyponormal operators. Integral Equations and Operator Theory 2005,53(1):51–60. 10.1007/s00020-003-1313-1 -quasihyponormal operators. Linear Algebra and Its Applications 2002,341(1–3):345–350.
-quasihyponormal operators. Linear Algebra and Its Applications 2002,341(1–3):345–350. operators. Mathematical Inequalities & Applications 2002,5(2):291–298.
operators. Mathematical Inequalities & Applications 2002,5(2):291–298. operators. Acta Scientiarum Mathematicarum 2004,70(1–2):279–287.
operators. Acta Scientiarum Mathematicarum 2004,70(1–2):279–287. -hyponormal operators. Proceedings of the American Mathematical Society 1997,125(12):3617–3624. 10.1090/S0002-9939-97-04004-5
-hyponormal operators. Proceedings of the American Mathematical Society 1997,125(12):3617–3624. 10.1090/S0002-9939-97-04004-5 -hyponormal operators. Proceedings of the American Mathematical Society 1995,123(8):2435–2440.
-hyponormal operators. Proceedings of the American Mathematical Society 1995,123(8):2435–2440. -quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.
-quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.