- Research
- Open access
- Published:
Laplace inverse and MR approach to existence of a unique solution and the Hyers–Ulam–Wright stability analysis of the nonhomogeneous fractional delay oscillation equation by matrix-valued fuzzy controllers
Journal of Inequalities and Applications volume 2022, Article number: 129 (2022)
Abstract
In this paper, we consider the nonhomogeneous fractional delay oscillation equation with order κ and investigate the existence of a unique solution in matrix-valued fuzzy Banach spaces for this equation using the alternative fixed point theorem. In a fuzzy environment, we introduce a class of the matrix-valued fuzzy Wright controller to investigate the Hyers–Ulam–Wright stability for the NH-FD-O equation with order κ. Finally, an illustrative example to demonstrate the application of the main theorem is also considered.
1 Introduction
One of the important topics in mathematics, and especially in mathematical analysis, is fractional calculus. Khusainov and Shuklin [1–3] applied the delayed exponential function and next matrix sine and a delayed matrix cosine to get the exact solution of a nonhomogeneous fractional delay oscillation equation (in short NH-FDO-E). In [4, 5], Li and Wang used a delayed Mittag-Leffler type matrix to solve a generalization of the mentioned problem.
In this paper, we consider the MVFB-space introduced in [6] and a modern class of MVF control functions based on the Wright functions. Our goal is to obtain an approximation for the NH-FDO-E by a new combined method powered by the Laplace inverse transform and MR approach in the MVFB-space [7–11]. Next, in Sect. 2, we present the basic definitions and concepts that are necessary to investigate the main results and introduce the matrix-valued fuzzy Wright function as a control function. In the third section, we prove the existence of a unique solution and the Hyers–Ulam–Wright stability for the NH-FDO-E in MVFN-spaces using the alternative FPT. Finally, we provide a numerical example as an application of our main theorem.
2 Preliminaries
In this manuscript, we consider the following NH-FDO-E:
where
-
\(\mathrm{k}: \mathfrak{L}\times \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) is an integrable function, \(\mathrm{u}(\mathfrak{x}) \in \mathbb{R}^{n}\), \(\rho \in \mathbb{R}^{n \times n}\) denotes constant matrix, \(\Upsilon \in C^{2}([-\xi ,0], \mathbb{R}^{n})\) for \(\xi >0\) being a fixed time.
-
\(D_{0}^{\kappa}\) is the standard Caputo fractional derivative with \(\kappa \in (1,2)\), defined by
$$ D_{0}^{\kappa} \mathrm{u}(\mathfrak{x})= \int _{0}^{\mathfrak{x}} \frac{(\mathfrak{x}-\mathit{t})^{1-\kappa}}{\Gamma (2-\kappa )} \mathrm{u}^{\prime \prime}(\mathit{t}) \,\mathrm{d} \mathit{t}, $$if the integral exists.
Definition 2.1
The Wright function is defined by the following series representation:
for \(\kappa >-1\), \(\varsigma >0\), \(\mathrm{k} \in \mathbb{R}\). It is an entire function of order \(1 /(1+\kappa )\), which has also been known as the generalized Bessel (or Bessel Maitland) function.
Now, we present the Laplace transforms.
Definition 2.2
([2])
The classical Laplace transform is defined by the integral formula
where \(\mathrm{k}(\mathfrak{x})\) is absolutely integrable on \([0,+\infty )\). Let \(J_{0}^{\kappa}\) denote the Riemann–Liouville fractional integral operator of order \(\kappa \in (1,2)\). Assume that the Laplace transforms of \(J_{0}^{\kappa}\mathrm{k}(\mathfrak{x})\) and \(D_{0}^{\kappa}\mathrm{k}(\mathfrak{x})\) exist for \(\mathfrak{x} \leq 0\) and the Laplace transform of \(\mathrm{k}(\mathfrak{x}-\mathrm{b})\) exists for \(\mathfrak{x} \leq \mathrm{b}\). Then we have
-
\(\mathcal{L} (J_{0}^{\kappa} \mathrm{k}(\mathfrak{x}) )( \mathfrak{r})=\mathfrak{r}^{-\kappa} \mathcal{L}(\mathrm{k}( \mathfrak{x}))(\mathfrak{r}) \),
-
\(\mathcal{L} (D_{0}^{\kappa} \mathrm{k}(\mathfrak{x}) )( \mathfrak{r})=\mathfrak{r}^{\kappa} \mathcal{L}(\mathrm{k}( \mathfrak{x}))(\mathfrak{r})-\mathfrak{r}^{\kappa -1} \mathrm{k}(0)- \mathfrak{r}^{\kappa -2} \mathrm{k}^{\prime}(0) \),
-
\(\mathcal{L} (\mathrm{k}_{1}(\mathfrak{x}) )(\mathfrak{r})=e^{- \mathrm{b} \mathfrak{r}} \int _{-\mathrm{b}}^{0} e^{-\mathfrak{x} \mathfrak{r}} \mathrm{k}(\mathfrak{x}) \,d \mathfrak{x}+e^{-\mathrm{b} \mathfrak{r}} \mathcal{L}(\mathrm{k}(\mathfrak{x}))(\mathfrak{r}) \).
Assuming \(\mathfrak{F}_{1}=[0,p]\), \(\mathfrak{F}_{2}=(0,{+\infty})\), \(\mathfrak{F}_{3}=(0,1]\), \(\mathfrak{F}_{4}=[0,{+\infty}]\), \(\mathfrak{F}_{5}=[0,1]\) (\(\mathfrak{F}_{5}^{\circ}=(0,1)\)), and \(\mathfrak{F}_{6} =[0,{+\infty})\), we consider the set of all matrices \(n \times n\) on \(\mathfrak{F}_{5}\) as follows:
For the above set, we have
-
\(\boldsymbol{\ell}=\operatorname{diag} [\ell _{1},\ldots , \ell _{n}]\), \(\boldsymbol{\jmath}=\operatorname{diag} [\jmath _{1},\ldots , \jmath _{n}] \in \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \);
-
\(\boldsymbol{\ell}\preceq \boldsymbol{\jmath} \) if and only if \(\ell _{i} \leq \jmath _{i} \) for every \(i=1, \ldots , n \);
-
\(\boldsymbol{\ell} \prec \boldsymbol{\jmath}\) denotes that \(\boldsymbol{\ell} \preceq \boldsymbol{\jmath}\) and \(\boldsymbol{\ell} \neq \boldsymbol{\jmath}\); \({\ell}_{1} < {\jmath}_{i}\) for every \(i=1, \ldots ,n\);
-
Define \(\boldsymbol{\mathrm{b}}=\operatorname{diag} [\mathrm{b},\ldots ,\mathrm{b}] \) in \(\operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5})\), where \(\mathrm{b} \in \mathfrak{F}_{5}\). Note that \(\operatorname{diag} [1,\ldots ,1]=\boldsymbol{1}\) and \(\operatorname{diag} [0,\ldots ,0]=\boldsymbol{0}\).
Definition 2.3
([6])
A mapping \(\circledast : \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5})\times \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \to \operatorname{diag} \mathrm{M}_{n}( \mathfrak{F}_{5})\) is called a GTN if:
-
(1)
\(\boldsymbol{\ell} {\circledast} \mathbf{1}=\boldsymbol{\ell} \) for all \(\boldsymbol{\ell} \in \operatorname{diag} \mathrm{M}_{n} ( \mathfrak{F}_{5})\) (boundary condition);
-
(2)
\(\boldsymbol{\ell} \circledast \boldsymbol{\jmath} = \boldsymbol{\jmath} \circledast \boldsymbol{\ell} \) for all \((\boldsymbol{\ell},\boldsymbol{\jmath}) \in (\operatorname{diag} \mathrm{M}_{n}( \mathfrak{F}_{5}))^{2}\) (commutativity);
-
(3)
\(\boldsymbol{\ell} \circledast (\boldsymbol{\jmath} \circledast \boldsymbol{\imath}) = (\boldsymbol{\ell} \circledast \boldsymbol{\jmath})\circledast \boldsymbol{\imath} \) for all \((\boldsymbol{\ell},\boldsymbol{\jmath}, \boldsymbol{\imath})\in (\operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}))^{3}\) (associativity);
-
(4)
\(\boldsymbol{\ell}_{1} \preceq \boldsymbol{\ell}_{2}\) and \(\boldsymbol{\jmath}_{1} \preceq \boldsymbol{\jmath}_{2} \) imply that \(\boldsymbol{\ell}_{1} \circledast \boldsymbol{\jmath}_{1} \preceq \boldsymbol{\ell}_{2}\circledast \boldsymbol{\jmath}_{2} \) for all \((\boldsymbol{\ell}_{1}, \boldsymbol{\jmath}_{2} ,\boldsymbol{\jmath}_{1},\boldsymbol{\jmath}_{2}) \in (\operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}))^{4} \) (monotonicity).
-
(5)
If for every \(\boldsymbol{\ell}, \boldsymbol{\jmath} \in \operatorname{diag} \mathrm{M}_{n}( \mathfrak{F}_{5})\) and each of sequences \(\{\boldsymbol{\ell}_{q}\}\) and \(\{\boldsymbol{\jmath}_{q}\}\) converges to ℓ and ȷ respectively, we get
$$ \lim_{q\rightarrow +\infty}(\boldsymbol{\ell}_{q}\circledast \boldsymbol{\jmath}_{q})= \boldsymbol{\ell} \circledast \boldsymbol{ \jmath},$$which implies the continuity of ⊛ on \(\operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5})\) (CGTN).
The following are numerical examples of CGTNs:
(i) Define \(\circledast _{M} : \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \times \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \to \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5})\) such that
then \(\circledast _{M}\) is CGTN (minimum CGTN). Here is an example of minimum CGTN:
or
(ii) Define \(\circledast _{P} : \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \times \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \to \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5})\) such that
then \(\circledast _{P}\) is CGTN (product CGTN). As an example of product CGTN,
or
(iii) Define \(\circledast _{L} : \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \times \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5}) \to \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{5})\) such that
then \(\circledast _{P}\) is CGTN (Lukasiewicz CGTN). A simple example of Lukasiewicz CGTN is
or
For the CGTNs introduced above, we clearly have the following relation:
Consider the matrix-valued fuzzy function (MVFF) \(\mathcal{A}: \mathfrak{F}_{1} \times \mathfrak{F}_{2} \to \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{3})\), then we have
-
It is left continuous and an increasing function.
-
\(\lim_{\eta \to {+\infty}}\mathcal{A}(\mathfrak{x},\eta )= \boldsymbol{1}\) for any \(\mathfrak{x} \in \mathfrak{F}_{1}\) and \(\eta \in \mathfrak{F}_{2}\).
-
For MVFFs \(\mathcal{A}\) and \(\mathcal{W}\), the relation “⪯” is defined as follows:
$$\begin{aligned} &\mathcal{A} \precsim \mathcal{W}\quad \text{if and only if} \quad \mathcal{A}( \mathfrak{x},\eta ) \preceq \mathcal{W}(\mathfrak{x}, \eta ) \quad \text{for all } \eta \in \mathfrak{F}_{2} \text{ and } \mathfrak{x} \in \mathfrak{F}_{1}. \end{aligned}$$
Definition 2.4
Let ⊛ be a CGTN, \(\mathcal{J}\) be a vector space, and \(\mathcal{A} :\mathcal{J} \times \mathfrak{F}_{2}\to \operatorname{diag} \mathrm{M}_{n}(\mathfrak{F}_{3})\) be a matrix-valued fuzzy set (MVFS). Triple \((\mathcal{J},\mathcal{A},\circledast )\) is called an MVFN-space if
-
(N1)
\(\mathcal{A}(\epsilon ,\eta )=\boldsymbol{1}\) if and only if \(\epsilon =0\) and \(\eta \in \mathfrak{F}_{2}\);
-
(N2)
\(\mathcal{A}({\varkappa} \epsilon ,\eta )=\mathcal{A}(\epsilon , \frac{\eta}{|\varkappa |})\) for all \(\epsilon \in \mathcal{J}\) and \(\varkappa \in \mathbb{C}\) with \(\varkappa \neq 0\);
-
(N3)
\(\mathcal{A}(\epsilon +w,\eta +\mathfrak{z})\succeq \mathcal{A}( \epsilon ,\eta )\circledast \mathcal{A}(w,\mathfrak{z})\) for all \(\epsilon , w \in \mathcal{J}\) and any \(\eta ,\mathfrak{z} \in \mathfrak{F}_{2}\);
-
(N4)
\(\lim_{\eta \to {+\infty}}\mathcal{A}(\mathfrak{x},\eta )= \boldsymbol{1}\) for any \(\eta \in \mathfrak{F}_{2}\).
When the MVFN-space is complete, we denote it by MVFB-space.
Using the concept of Wright function [13], we define an MVF Wright function \(\boldsymbol{ W_{\kappa ,\varsigma}}\) (\(\boldsymbol{\kappa ,\varsigma}\in \mathfrak{F}_{2}\)) as a control function in the MVFN-spaces by
where the Wright function \(W_{\kappa ,\varsigma}\) is defined as follows:
Then, for the MVF Wright function \(\boldsymbol{ W_{\kappa ,\varsigma}}\), we have
-
It is left continuous and an increasing function for positive values.
-
\(\lim_{\eta \to {+\infty}}\boldsymbol{ W_{\kappa ,\varsigma}}(- \frac{|\mathfrak{x}|}{\eta}) =\boldsymbol{1}\).
-
For \(\boldsymbol{ W_{\kappa ,\varsigma}}\) and the matrix-valued fuzzy function \(\boldsymbol{ \Xi _{\kappa ,\varsigma}}\), we have
$$ \boldsymbol{ \Xi _{\kappa ,\varsigma}}\precsim \boldsymbol{ W_{\kappa ,\varsigma}} \quad \text{if and only if}\quad \boldsymbol{ \Xi _{\kappa ,\varsigma}} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\eta} \biggr) \preceq \boldsymbol{ W_{\kappa ,\varsigma}} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\eta} \biggr),$$
and we further get
-
(a)
\(\boldsymbol{ W_{\kappa ,\varsigma}} (- \frac{|\mathfrak{x}|}{\eta} ) >0\).
-
(b)
For \(\eta \in \mathfrak{F}_{2}\), \(\boldsymbol{ W_{\kappa ,\varsigma}} (- \frac{|\mathfrak{x}|}{\eta} )=\boldsymbol{1} \) if and only if \(\mathfrak{x} =0\).
First, we assume that \(\boldsymbol{ W_{\kappa ,\varsigma}} (- \frac{|\mathfrak{x}|}{\eta} )=\boldsymbol{1}\). Then
$$\begin{aligned} &\operatorname{diag} \biggl[W_{\kappa ,\varsigma} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\eta} \biggr),W_{\kappa ,\varsigma} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\eta} \biggr), W_{\kappa ,\varsigma} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\eta} \biggr) \biggr] \\ &\quad = \operatorname{diag} \Biggl[\sum_{\mathfrak{p}=0}^{+\infty} \frac{ ({\frac{- \vert \mathfrak{x} \vert }{\eta}} )^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{ ({\frac{- \vert \mathfrak{x} \vert }{\eta}} )^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{ ({\frac{- \vert \mathfrak{x} \vert }{\eta}} )^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )} \Biggr] = \boldsymbol{1}, \end{aligned}$$then \(\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{-|\mathfrak{x}|}{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}=1\). We have
$$\begin{aligned} 1+ \sum_{\mathfrak{p}=1}^{+\infty} \frac{({\frac{- \vert \mathfrak{x} \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}=1 \quad \text{implies}\quad \sum_{\mathfrak{p}=1}^{+\infty} \frac{({\frac{- \vert \mathfrak{x} \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}=0, \end{aligned}$$therefore
$$ \vert \mathfrak{x} \vert =0 \quad \text{and}\quad \mathfrak{x}=0.$$Conversely, suppose that \(\mathfrak{x} =0\), then \(\sum_{\mathfrak{p}=1}^{+\infty} \frac{({\frac{-|\mathfrak{x}}{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}=0\). As a result
$$\begin{aligned} \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \mathfrak{x} \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}= 1+ \sum_{\mathfrak{p}=1}^{+\infty} \frac{({\frac{- \vert \mathfrak{x} \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}=1 \end{aligned}$$yields
$$ \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \mathfrak{x} \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}=1.$$ -
(c)
We shall deduce
$$ \boldsymbol{ W_{\kappa ,\varsigma}}\biggl(- \frac{ \vert \alpha (\mathfrak{x}) \vert }{\eta}\biggr) = \boldsymbol{ W_{\kappa ,\varsigma}}\biggl(- \frac{ \vert (\mathfrak{x}) \vert }{\frac{\eta}{ \vert \alpha \vert }}\biggr).$$Indeed,
$$\begin{aligned} &\boldsymbol{ W_{\kappa ,\varsigma}}\biggl(-\frac{ \vert \mathfrak{x}) \vert }{\eta}\biggr) \\ &\quad =\operatorname{diag} \Biggl[\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \alpha (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \alpha (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \alpha (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )} \Biggr] \\ &\quad =\operatorname{diag} \Biggl[\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \alpha \vert \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \alpha \vert \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \alpha \vert \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )} \Biggr] \\ &\quad =\operatorname{diag} \Biggl[\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\frac{\eta}{ \vert \alpha \vert }})^{\mathfrak{p}}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\frac{\eta}{ \vert \alpha \vert }})^{\mathfrak{p}}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\tau +\omega )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\frac{\eta}{ \vert \alpha \vert }}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa +\varsigma )} \Biggr] \\ &\quad=\boldsymbol{ W_{\kappa ,\varsigma}}\biggl(- \frac{ \vert (\mathfrak{x}) \vert }{\frac{\eta}{ \vert \alpha \vert }}\biggr). \end{aligned}$$ -
(d)
Finally, we prove
$$\begin{aligned} &\boldsymbol{ W_{\kappa ,\varsigma}}\biggl(- \frac{ \vert (\mathfrak{x}+ \epsilon ) \vert }{\eta +\zeta}\biggr) \succeq \boldsymbol{ W_{\kappa ,\varsigma}}\biggl(-\frac{ \vert \mathfrak{x} \vert }{\eta}\biggr) \circledast \boldsymbol{ W_{\kappa ,\varsigma}}\biggl(- \frac{ \vert \epsilon \vert }{\zeta}\biggr) . \end{aligned}$$Suppose that \(\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{|(\mathfrak{x})|}{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )} \leq \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{|\epsilon |}{\zeta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )} \), then
$$ \frac{- \vert (\mathfrak{x}) \vert }{\eta} \leq \frac{- \vert \epsilon \vert }{\zeta}$$implies
$$\begin{aligned} &\frac{ \vert (\mathfrak{x}) \vert }{\eta} \geq \frac{ \vert \epsilon \vert }{\zeta}, \\ &\frac{\zeta \vert \mathfrak{x} \vert }{\eta}\geq \vert \epsilon \vert , \\ &\frac{\zeta \vert (\mathfrak{x}) \vert }{\eta} + \bigl\vert (\mathfrak{x}) \bigr\vert \geq \bigl\vert ( \epsilon ) \bigr\vert + \vert \mathfrak{x} \vert , \end{aligned}$$then
$$\begin{aligned} &\frac{\zeta \vert (\mathfrak{x}) \vert }{\eta} + \bigl\vert (\mathfrak{x}) \bigr\vert \geq \bigl\vert ( \mathfrak{x}) +(\epsilon ) \bigr\vert , \\ &\bigl\vert (\mathfrak{x}) \bigr\vert \biggl(\frac{\zeta}{\eta}+1\biggr) \geq \bigl\vert (\mathfrak{x} ) +( \epsilon ) \bigr\vert , \\ &\bigl\vert (\mathfrak{x}) \bigr\vert \biggl(\frac{\zeta +\eta}{\eta}\biggr)\geq \bigl\vert (\mathfrak{x}) +( \epsilon ) \bigr\vert , \\ &\frac{ \vert (\mathfrak{x}) \vert }{\eta}\geq \frac{ \vert (\mathfrak{x}) +(\epsilon ) \vert }{\zeta +\eta}, \\ &\frac{- \vert (\mathfrak{x}) \vert }{\eta}\leq \frac{- \vert (\mathfrak{x} ) +(\epsilon ) \vert }{\zeta +\eta} \end{aligned}$$yields
$$ \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x} ) +(\epsilon ) \vert }{\zeta +\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )} \geq \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}.$$Therefore, we have
$$\begin{aligned} & \operatorname{diag} \Biggl[\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) +(\epsilon ) \vert }{\eta +\zeta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) +(\epsilon ) \vert }{\eta +\zeta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{ \vert \alpha \vert (- \vert (\mathfrak{x} ) +(\epsilon ) \vert )}{\eta +\zeta})^{\mathfrak{p}}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )} \Biggr] \\ &\quad {} \succeq\operatorname{diag} \Biggl[\sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}, \sum_{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}, \sum_{\mathfrak{p}=0}^{\infty} \frac{({\frac{- \vert (\mathfrak{x}) \vert }{\eta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa ,\varsigma )} \Biggr] \\ &\qquad {}\circledast\operatorname{diag} \Biggl[\sum _{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \epsilon \vert }{\zeta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}, \sum _{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert \epsilon \vert }{\zeta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )}, \sum _{\mathfrak{p}=0}^{+\infty} \frac{({\frac{- \vert (\epsilon ) \vert }{\zeta}})^{\mathfrak{p}}}{\mathfrak{p}! \Gamma (\mathfrak{p}\kappa + \varsigma )} \Biggr]. \end{aligned}$$
Consequently, if
for \(\eta \in \mathfrak{F}_{2}\), then \((\mathcal{J},\mathcal{A},\circledast _{M})\) is an MVFN-space. From now on, we assume \(\circledast =\circledast _{M}\).
Theorem 2.1
([14])
Consider the \(\mathfrak{F}_{4}\)-valued metric space \((\mathcal{Z},d)\). For \(\mathrm{u}, \mathrm{v} \in \mathcal{Z}\), let Δ be the self mapping on \(\mathcal{Z}\) such that
where \(0 < \lambda <1\) is a Lipschitz constant. Let \(\mathrm{u} \in \mathcal{Z}\), then we have either
-
(i)
\(d (\Delta ^{\mathbf{q}} \mathrm{u}, \Delta ^{\mathbf{q}+1} \mathrm{u} )=+\infty \) for all \(\mathbf{q} \in \mathbb{N}\)
or
-
(ii)
we can find \(\mathbf{q}_{0} \in \mathbb{N}\) such that \(d (\Delta ^{\mathbf{q}} \mathrm{u}, \Delta ^{\mathbf{q}+1} \mathrm{u} )<+\infty \) for all \(\mathbf{q} \geq \mathbf{q}_{0} \).
If condition (ii) holds, then we always have
-
(1)
the fixed point \(\mathrm{v}^{*}\) of Δ is the convergent point of the sequence \(\{\Delta ^{\mathbf{q}} \mathrm{u} \}\);
-
(2)
in the set \(\mathcal{Z}^{*}= \{\mathrm{v} \in \mathcal{Z} \mid d ( \Delta ^{\mathbf{q}_{0}} \mathrm{u}, \mathrm{v} )<+\infty \}, \mathrm{v}^{*}\) is the unique fixed point of Δ;
-
(3)
\((1-\lambda ) \,d (\mathrm{v}, \mathrm{v}^{*} ) \leq d( \mathrm{v}, \Delta \mathrm{v})\) for every \(\mathrm{v} \in \mathcal{Z}\).
Definition 2.5
Consider the MVF \(\boldsymbol{ W_{\kappa ,\varsigma}}\). We say (1) has Hyers–Ulam–Wright stability when a given differentiable map \(\mathrm{v}(\mathfrak{x})\) satisfies
for \(\mathfrak{x}\in \mathfrak{F}_{1}\) and there is a solution \(\mathrm{u}(\mathfrak{x})\) of (1) such that, for some \(\lambda >0\),
3 Hyers–Ulam–Wright stability for nonhomogeneous fractional delay oscillation equation
Now, we use a new method, the Laplace–Mihet–Radu method, to show (1) is Hyers–Ulam–Wright stable [12] in MVFB-space \((\mathcal{J},\mathcal{A},\circledast )\) with MVFF \(\boldsymbol{W_{\kappa ,\varsigma}}\).
We choose the set \(\mathcal{Z}\) as follows:
and define the mapping \(d:\mathcal{Q}\times \mathcal{Q}\rightarrow [0,+\infty ]\) as
Theorem 3.1
The \(\mathfrak{F}_{4}\)-valued metric space \((\mathcal{Q}, d)\) is complete.
Proof
We have \(d(\mathrm{u},\mathrm{v})=0\) iff \(\mathrm{u}=\mathrm{v}\). Assuming that \(d(\mathrm{u},\mathrm{v})=0\), then we come to
and so
for all \(\wp \in \mathfrak{F}_{6}\). Let \(\wp \to 0\) in (4), we get
Thus \(\mathrm{u}(\mathfrak{x})=\mathrm{v}(\mathfrak{x})\) for every \(\mathfrak{x} \in \mathfrak{F}_{1}\) and vice versa. Also we have \(d(\mathrm{u},\mathrm{v})=d(\mathrm{v},\mathrm{u})\) for every \(\mathrm{u},\mathrm{v}\in \mathcal{Q}\). Assuming \(d(\mathrm{u},\mathrm{v})=\alpha _{1}\in{\mathfrak{F}_{2}}\) and \(d(\mathrm{v},\mathrm{w})=\alpha _{2}\in{\mathfrak{F}_{2}}\), then we have
and
for every \(\eta \in \mathfrak{F}_{2} \). Therefore, we get
This infers that \(d(\mathrm{v},\mathrm{w})\le d(\mathrm{u},\mathrm{v})+d(\mathrm{v}, \mathrm{w})\). To show the completeness of \((\mathcal{Q}, d)\), we suppose that \(\{\mathrm{v}_{\mathbf{q}}\}_{k}\) is a Cauchy sequence in \((\mathcal{Q}, d)\). Assume that \(\mathfrak{x} \in \mathfrak{F}_{1}\), \(\tau \in{\mathfrak{F}_{2}}\), \(\Im \in{\mathfrak{F}_{5}}^{\circ}\), and \(\eta \in{\mathfrak{F}_{2}}\) in which \(\boldsymbol{ W_{\kappa ,\varsigma}} (- \frac{|\mathfrak{x}|}{\eta} ) \succ \boldsymbol{ 1-\Im}\). For \(\alpha \eta <\tau \), choose \(\mathbf{q}_{0}\in {\mathbb{N}}\) such that
Then
and so
which implies that the sequence \(\{ \mathrm{v}_{\mathbf{q}}(\mathfrak{x})\}_{k}\) is Cauchy in the complete space \((\mathcal{J},\mathcal{A},\circledast )\) on a compact set \(\mathfrak{F}_{1}\). Then it is uniformly convergent to the mapping \(\mathrm{v}:\mathfrak{F}_{1}\to \mathcal{J}\). By the uniform convergence property we conclude that \(\mathrm{v}\in \mathcal{Q}\), and then \((\mathcal{Q}, d)\) is complete. □
Now, we can investigate Hyers–Ulam–Wright stability and get an approximation for the nonhomogeneous fractional delay oscillation equation (1).
Theorem 3.2
Consider the MVFB-space \((\mathcal{J},\mathcal{A},\circledast )\) and the constant θ such that \(0<\theta <1\). Suppose that the following conditions hold:
- ▶:
-
By considering the MVFF
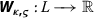 as the control function, we have $$\begin{aligned} & \boldsymbol{ W_{\kappa ,\varsigma}} \biggl( \frac{- \vert \mathcal{L} ((\mathfrak{r}))(\mathfrak{x}) \vert }{\eta} \biggr){ \succeq} \boldsymbol{ W_{\kappa ,\varsigma}} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\frac{\eta}{ \theta}} \biggr). \end{aligned}$$(5)
as the control function, we have $$\begin{aligned} & \boldsymbol{ W_{\kappa ,\varsigma}} \biggl( \frac{- \vert \mathcal{L} ((\mathfrak{r}))(\mathfrak{x}) \vert }{\eta} \biggr){ \succeq} \boldsymbol{ W_{\kappa ,\varsigma}} \biggl(- \frac{ \vert \mathfrak{x} \vert }{\frac{\eta}{ \theta}} \biggr). \end{aligned}$$(5)
Let \(\mathrm{v}:\mathfrak{F}_{1}\rightarrow \mathcal{J}\) be a differentiable function satisfying
Then we can find a unique solution \(\mathrm{u}:\mathfrak{F}_{1}\rightarrow \mathcal{J}\) for equation (1) such that
where \(\digamma =\frac{\theta}{1-\theta}\), and for every \(\mathfrak{x} \in \mathfrak{F}_{1}\) and \(\eta \in{\mathfrak{F}_{2}}\).
Proof
Consider complete \({\mathfrak{F}_{4}}\)-valued metric space \((\mathcal{Q}, d)\) defined in Theorem 3.1.
Step 1. According to the main equation, we define the mapping \(\Delta : \mathcal{Q}\rightarrow \mathcal{Q}\) as follows:
for \(\mathfrak{x} \in \mathfrak{F}_{1} \), and we show that Δ is a strictly contractive mapping.
Let \(\mathrm{u},\mathrm{v}\in \mathcal{Q}\) and consider the coefficient \(B_{\mathrm{u}\mathrm{v}}\in \mathfrak{F}_{4}\) with \(d(\mathrm{u},\mathrm{v})\leq {B}_{\mathrm{u}\mathrm{v}}\), thus
for all \(\mathrm{u},\mathrm{v} \in \mathcal{Q}\), \(\mathfrak{x} \in \mathfrak{F}_{1}\), and \(\eta \in {\mathfrak{F}_{2}}\). Applying (N2) and (N3), we have
which implies that
and so
where \(0< \theta <1\), therefore Δ is a contractive mapping.
Step 2. We will show that \(d(\Delta (\mathrm{v}),\mathrm{v})<+\infty \).
Let \(\mathrm{v}\in \mathfrak{L}\), we have
Consequently,
for every \(\eta \in{\mathfrak{F}_{2}}\). Then we have \(d(\Delta \mathrm{v},\mathrm{v})<{+\infty}\).
Therefore, all the conditions in (ii) of Theorem 2.1 hold. Then we have
-
(1)
The sequence \(\{\Delta ^{\mathbf{q}} \mathrm{v}\}\) converges to a fixed point such as v.
-
(2)
The unique element v is in the set \(\mathcal{Q}^{\ast}=\{ \mathrm{v}\in \mathcal{Q}: d(\Delta \mathrm{v}, \mathrm{v})<+\infty \}\) and is the unique fixed point of Δ, it means that \(\Delta \mathrm{v}=\mathrm{v}\) or equivalently
$$\begin{aligned} \mathrm{v}(\mathfrak{x})&= \bigl(\mathfrak{r}^{\kappa}+\rho e^{- \mathfrak{r}\xi}\bigr)\mathcal{L}\bigl(\mathrm{u}(\mathfrak{x})\bigr) ( \mathfrak{r})- \mathfrak{r}^{\kappa -1} \Upsilon (0) \\ &\quad{}-\mathfrak{r}^{\kappa -2}\Upsilon ^{\prime}(0)+\rho e^{-\mathfrak{r} \xi} \int _{-\xi}^{0} e^{-\mathfrak{r}\xi}\Upsilon ( \mathfrak{x}) \,\mathrm{d}\mathfrak{x} - \mathcal{L}\bigl(\mathrm{k}(\mathfrak{x}) \bigr) ( \mathfrak{r}). \end{aligned}$$(11)
Since u is a differentiable function, by the NH-FDO-E and according to equation (11), we have

-
(3)
Using inequality (10), we get
$$\begin{aligned} d(\mathrm{u},\mathrm{v}) \leq \frac{1}{1-\theta}d(\Delta \mathrm{v}, \mathrm{v}) \leq \frac{\varpi \theta}{1-\theta}, \end{aligned}$$thus, equation (1) has the Hyers–Ulam–Wright stability property.
Now, we show the uniqueness of the obtained point. For convenience, we consider

and let h be another differentiable function satisfying equation (12), and this means that the following equation holds:

We are ready to prove that h is a fixed point of Δ and \(\mathrm{h}\in \mathcal{Q}^{\ast}\). Using equation (13), we get \(\Delta \mathrm{h}= \mathrm{h}\). Now, we show that \(d(\Delta \mathrm{v}, \mathrm{h})<+\infty \). Let \(\mathrm{v}\in \mathcal{Q}\),  , and using equation (13), we get
, and using equation (13), we get

then

□
4 Example
Now, we provide a numerical example to demonstrate the main results obtained.
Example 4.1
Consider the following the NH-FDO-E:
where \(\kappa =\frac{1}{2}\), \(\xi =\frac{1}{7}\), and . Assume that the following condition is true for the given continuous function:
- ▶:
-
$$\begin{aligned} & \boldsymbol{ W_{\frac{1}{2},\varsigma}} \biggl( - \frac{ \vert \mathcal{L} ((s))(\mathfrak{x}) \vert }{\eta} \biggr)\succeq \boldsymbol{ W_{\frac{1}{2},\varsigma}} \biggl(- \frac{ \vert \mathfrak{x} \vert }{4\eta} \biggr). \end{aligned}$$
Let  be a differentiable function such that
be a differentiable function such that
then v is a solution of the inequality
where \(\Upsilon (\mathfrak{x})=[3 \mathfrak{x}, 4 \mathfrak{x}^{2}]^{T}\). Thus we can find a unique differentiable function  from (14) such that for each \(\varrho \in [1,2]\) we have
from (14) such that for each \(\varrho \in [1,2]\) we have
Therefore,
and
where in \(\digamma =\frac{1}{3}\). See Fig. 1.
Graphs related to the exact solution of the NH-FDO-E (14) for \(\xi =\frac{1}{7}\), \(\kappa =\frac{1}{2}\)
Availability of data and materials
Not applicable.
References
Khusainov, D.Y., Shuklin, G.V.: On relative controllability in systems with pure delay. Int. Appl. Mech. 41(2), 210–221 (2005). (Russian); translated from Prikl. Mekh. 41 (2005), no. 2, 118–130
Liu, L., Dong, Q., Li, G.: Exact solutions and Hyers-Ulam stability for fractional oscillation equations with pure delay. Appl. Math. Lett. 112, 106666 (2021). 7 pp.
Khusainov, D.Y., Diblik, J., Ruzhichkova, M., Lukacheva, J.: A representation of the solution of the Cauchy problem for an oscillatory system with pure delay. Nonlinear Oscil. 11(2), 276–285 (2008)
Li, M., Wang, J.: Finite time stability and relative controllability of Riemann-Liouville fractional delay differential equations. Math. Methods Appl. Sci. 42(18), 6607–6623 (2019)
Li, M., Wang, J.: Exploring delayed Mittag-Leffler type matrix functions to study finite time stability of fractional delay differential equations. Appl. Math. Comput. 324, 254–265 (2018)
Eidinejad, Z., Saadati, R., de la Sen, M.: Radu-mihet method for the existence, uniqueness, and approximation of the ψ-Hilfer fractional equations by matrix-valued fuzzy controllers. Axioms 10(2), 63 (2021)
Arfan, M., Shah, K., Abdeljawad, T., Hammouch, Z.: An efficient tool for solving two-dimensional fuzzy fractional-ordered heat equation. Numer. Methods Partial Differ. Equ. 37(2), 1407–1418 (2021)
Younus, A., Muhammad, A., Usama, A., Tehmina, B., Abdeljawad, T.: Some fundamental results on fuzzy conformable differential calculus. J. Fract. Calc. Nonlinear Syst. 2(2), 31–61 (2021)
Arfan, M., Shah, K., Ullah, A., Abdeljawad, T.: Study of fuzzy fractional order diffusion problem under the Mittag-Leffler kernel law. Phys. Scr. 96(7), 074002 (2021)
Younus, A., Asif, M., Atta, U., Bashir, T., Abdeljawad, T.: Analytical solutions of fuzzy linear differential equations in the conformable setting. J. Fract. Calc. Nonlinear Syst. 2(2), 13–30 (2021)
Arfan, M., Shah, K., Abdeljawad, T., Hammouch, Z.: An efficient tool for solving two-dimensional fuzzy fractional-ordered heat equation. Numer. Methods Partial Differ. Equ. 37(2), 1407–1418 (2021)
Kiryakova, V.: Some special functions related to fractional calculus and fractional (noninteger) order control systems and equations. Facta Univ. Ser. Autom. Control Robot. 7(1), 79–98 (2008)
Podlubny, I.: Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego (1999)
Diaz, J.B., Margolis, B.: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bull. Am. Math. Soc. 74, 305–309 (1968)
Acknowledgements
The authors are thankful to the area editor and referees for giving valuable comments and suggestions.
Funding
Chenkuan Li is supported by NSERC Discovery Grant number 2019-03907.
Author information
Authors and Affiliations
Contributions
ZE, writing—original draft preparation. RS, writing—original draft preparation and project administration. CL, methodology and project administration. All authors have read and agreed to the published version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eidinejad, Z., Saadati, R. & Li, C. Laplace inverse and MR approach to existence of a unique solution and the Hyers–Ulam–Wright stability analysis of the nonhomogeneous fractional delay oscillation equation by matrix-valued fuzzy controllers. J Inequal Appl 2022, 129 (2022). https://doi.org/10.1186/s13660-022-02869-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-022-02869-y
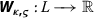 as the control function, we have
as the control function, we have 