- Research
- Open access
- Published:
Continuous controlled cone metric-type spaces over real Banach algebras and fixed-point results
Journal of Inequalities and Applications volume 2022, Article number: 52 (2022)
Abstract
In this article, we introduce a new geometrical structure that is the hybrid of a cone metric space over Banach algebra and a controlled metric-type space. We introduce a new metric space and prove analogs of Banach-, Kannan- and Reich-type fixed-point theorems. We also furnish various concrete examples to establish the validity of our results. The obtained results generalize many well-known results in the literature.
1 Introduction
In 2018, Mlaiki et al. [1] proposed the idea of controlled metric-type spaces that is the generalization of a b-metric space [2]. For more information on b-metric spaces and more generalizations, see [3–6]. They used \(\theta:\mathcal{U}\times \mathcal{U}\to [1,\infty )\) instead of b in the triangular inequality condition by a different approach from Kamran et al. [7] who proposed the idea of extended b-metric spaces. They established a Banach-like contraction and proved some fixed-point results in such spaces. This shows that the class of such type of spaces is much more larger than the class of b-metric spaces and the class of metric spaces. Using the idea of a controlled metric-type space, several authors have published a number of papers in different directions (see [8–10]).
In 2007, Huang and Zhang [11] initiated the concept of a cone metric space over a Banach space as the generalization of metric spaces. They used an ordered Banach space E instead of \(\mathbb{R}\) as the range set of metric d, i.e., they used \(d:X\times X \to E\). They also discussed Banach-type contraction and proved some fixed-point results. Then, many researchers gave attention to the study of fixed-point results in such spaces. Rough estimates show that, more than six hundred papers have been published dealing with the cone metric spaces [12]. However, recently, some scholars obtained that a cone metric space \((X,d)\) is equivalent to the usual metric space \((X,d^{*} )\), where they defined the real-valued metric function \(d^{*}\) as the nonlinear scalarization function \(\xi _{e}\) [13]. However, the current situation altered when Liu and Xu [14] introduced cone metric spaces over a real Banach algebra. They defined generalized Lipschitz mapping and proved some fixed theorems. They established a concrete example to elucidate that the fixed-point results in cone metric spaces over Banach algebras are not equivalent to those in metric spaces. Later, in 2016, Huang and Radenovic [15] extended the idea of a cone metric space over Banach algebras to cone b-metric spaces over Banach algebras. They proved Banach- and Kannan-type theorems for such spaces (see also [16]).
In 1971, Reich [17] introduced a new type of contraction that we call Reich contraction. It was a generalization of the well-known Banach contraction and Kannan contraction (see [18, 19]). On the other hand, Samet et al. [20] initiated the idea of α-admissible mapping in metric spaces. Recently, Malhotra et al. [21, 22] used the idea of α-admissibility in cone metric spaces over Banach algebras and proved Banach-type and Kannan-type theorems. Later, in 2017, Hussain et al. [23] used the concept of α-admissible mapping in cone b-metric spaces over Banach algebras and proved Banach-type results in such spaces.
In this paper, we introduce the definition of a controlled cone metric-type space over a Banach algebra and then we prove some fixed-point results. We also furnish an example to show the validity of our obtained results. The last section of this paper consists of some important consequences of our results. Throughout the paper, we will use only real Banach algebras with identity.
2 Preliminaries
Let \((\mathcal{A},\Vert \cdot \Vert )\) be a real Banach algebra with zero element θ. A cone \(\mathcal{K}\) in \(\mathcal{A}\) is a nonempty closed subset of \(\mathcal{A}\) such that \(\mathcal{P}^{2}=\mathcal{P}\cdot \mathcal{P}\subseteq \mathcal{P}, \mathcal{P}\cap (-\mathcal{P})={\theta},\mathcal{P}+\mathcal{P} \subseteq \mathcal{P}\) and \(\lambda \mathcal{P} \subseteq \mathcal{P}\) for all \(\lambda \geq 0\). If the interior of \(\mathcal{K}\) denoted by int\(\mathcal{K}\) is nonempty, then the cone \(\mathcal{K}\) is called a solid cone. If we define a relation ⪯ on \(\mathcal{A}\) by \(t\preceq v\) if and only if \(v-t \in \mathcal{K}\), then ⪯ is a partial order on \(\mathcal{A}\). We write \(t \ll c v\) if and only if \(v-t \in \mathcal{K}\) and \(t\ne v\). Define another partial order ≪ on \(\mathcal{A}\) by \(t\ll v\) if and only if \(v-t\in \) int\(\mathcal{K}\). A cone \(\mathcal{K}\) in \(\mathcal{A}\) is said to be a normal cone if for all \(t, v \in \mathcal{A}\) with \(\theta \preceq t \preceq v\), there exists a real number \(M>0\) such that \(\Vert t\Vert \leq M \Vert v\Vert \). The normal constant of \(\mathcal{K}\) is the least positive constant M for which the above inequality holds.
Let \((\mathcal{A},\Vert \cdot \Vert )\) be a unital Banach algebra with identity element e. An element \(t\in \mathcal{A}\) is said to be invertible if there exists \(v \in \mathcal{A}\) such that \(tv=vt=e\). A complex number \(\lambda \in \mathbb{C}\) is said to be the spectral value of \(v\in \mathcal{A}\) if \(v-\lambda e\) is noninvertible in \(\mathcal{A}\). The set of all spectral values of \(v\in \mathcal{A}\) that is denoted by \(\sigma (v)\) is called the spectrum of v. The number \(r_{\sigma}(v)\) (or \(r(v)\)) defined by \(r_{\sigma}(v)=\sup \{|\lambda |: \lambda \in \sigma (v)\}\) is called the spectral radius of \(v\in \mathcal{A}\).
Lemma 2.1
([24])
Let \(\mathcal{A}\) be a Banach algebra with identity e. Then, the spectral radius \(r(v)\) of \(v\in \mathcal{A}\) satisfies
Furthermore, if \(r(v)< |\lambda |\) for some \(v\in \mathcal{A}\), then \((\lambda e-v)\) is invertible,
Lemma 2.2
([24])
Let \(\mathcal{A}\) be a Banach algebra and \(u, v \in \mathcal{A}\). If u and v commute, then
Definition 2.3
([25])
Consider a Banach algebra \(\mathcal{A}\) with solid cone \(\mathcal{K}\). A c-sequence is a sequence \(\{u_{n}\}\) in \(\mathcal{K}\) such that for every \(c\gg \theta \), there exists \(N\in \mathbb{N}\) such that \(u_{n}\ll c\) for all \(n\geq N\).
Lemma 2.4
([15])
Let \(\alpha, \beta \in \mathcal{K}\) be two arbitrary vectors and \(\{u_{n}\}\), \(\{q_{n}\}\) be two sequences in a solid cone \(\mathcal{K}\) of a Banach algebra \(\mathcal{A}\). Then, \(\{\alpha u_{n}+\beta q_{n}\}\) is a c-sequence.
Lemma 2.5
([26])
Let \(\mathcal{A}\) be a Banach algebra and \(\mathcal{K}\) be a cone in \(\mathcal{A}\) (it need not be a normal cone). Then, the following hold:
- \((u_{1})\):
-
If for each \(c \in \operatorname{int}\mathcal{K}, \theta \preceq p \ll c\), then \(p=\theta \).
- \((u_{2})\):
-
If \(p\in \mathcal{K}\) is such that \(r(p)<1\), then \(\Vert p^{n}\Vert \to 0\) as \(n\to \infty \).
- \((u_{3})\):
-
Let \(c \in \operatorname{int}\mathcal{K}\) and \(q_{n}\to \theta \) in \(\mathcal{A}\) as \(n\to \infty \). Then, there exists \(N\in \mathbb{N}\) such that \(q_{n}\ll c\) for all \(n\geq N\).
- \((u_{4})\):
-
If \(p \preceq pk\), where \(p, k \in \mathcal{K}\) and \(r(k)<1\), then \(p=\theta \).
Definition 2.6
([15])
Let \(\mathfrak{X}\) be a nonempty set and \(b\geq 1\) be a constant. A mapping \(d_{b}:\mathfrak{X} \times \mathfrak{X} \to \mathcal{A}\) is called a cone b-metric over a Banach algebra \(\mathcal{A}\) if the following axioms hold:
- \((B_{1} )\):
-
for all \(p,t \in \mathfrak{X}, d_{b}(p,t) \succeq \theta \) and \(d_{b}(p, t)=\theta \) if and only if \(p=t \);
- \((B_{2} )\):
-
for all \(p,t \in \mathfrak{X}, d_{b}(p, t)=d_{b}(t, p) \);
- \((B_{3} )\):
-
for all \(p,t,u \in \mathfrak{X}\), there exists \(b \geq 1\) such that \(d_{b}(p, u)\preceq b[d_{b}(p, t)+d_{b}(t, u)]\).
The pair \((\mathfrak{X},d_{b})\) is called a cone b-metric space over a Banach algebra \(\mathcal{A}\).
Remark 2.7
If \(b=1\), then we say that \(d_{1}\) is a cone metric over a Banach algebra \(\mathcal{A}\). Hence, we can say that a cone b-metric is a generalization of a cone metric.
Example 2.8
Consider the Banach algebra \(\mathcal{A}=C([0,1])\) with unit element \(e(t)=1\) and supremum norm where multiplication is defined point-wise. Let \(\mathfrak{X}=\mathbb{R}\) and \(\mathcal{K}=\{f\in \mathcal{A}: f(l)\geq 0; \forall l \in [0,1] \} \). Define \(d_{b}:\mathfrak{X} \times \mathfrak{X} \to \mathcal{A}\) by
Then, \(d_{b}\) is a cone b-metric on \(\mathfrak{X}\) over a Banach algebra \(\mathcal{A}\) with \(b=2^{a-1}\), but it is not a cone metric on \(\mathfrak{X}\).
Definition 2.9
([15])
Let \(\{ u_{k}\}\) be a sequence in \(\mathfrak{X}\) where \((\mathfrak{X},d_{b})\) is a cone b-metric space over a Banach algebra \(\mathcal{A}\). Then, \(\{ u_{k}\}\) is said to be
-
(i)
a convergent sequence that converges to \(p\in \mathfrak{X}\) if for every c∈ int\(\mathcal{K} (i.e., \theta \ll c)\), there exists a natural number N such that \(d_{b}(u_{k},p)\ll c\) for all \(k\geq N\);
-
(ii)
a Cauchy sequence if for every c∈ int\(\mathcal{K} (i.e., \theta \ll c)\), there exists a natural number N such that \(d_{b}(u_{k},u_{i})\ll c\) for all \(k, i \geq N\).
The pair \((\mathfrak{X},d_{b})\) is said to be a complete cone b-metric space if every Cauchy sequence in \(\mathfrak{X}\) is convergent in \(\mathfrak{X}\).
Remark 2.10
(i) If \(\{ p_{n}\}\) converges to p in \(\mathfrak{X}\), then \(\{d_{b}(p_{k}, p) \}\) and \(\{d_{b}(p_{k}, p_{k+i}) \}\) are c-sequences for any \(i \in \mathbb{N}\).
(ii) If \(\Vert p_{k}\Vert \to 0 \) as \(k \to \infty \), then for any \(c \gg \theta \), there exists \(N \in \mathbb{N}\) such that for all \(n> N\) we have \(p_{k} \ll c\).
Definition 2.11
([1])
Let \(\mathfrak{X}\) be a nonempty set and \(s:\mathfrak{X} \times \mathfrak{X} \to [1,\infty )\). A function \(d_{s}:\mathfrak{X} \times \mathfrak{X} \to [0,\infty ) \) is called a controlled metric type if for all \(p,v,t \in \mathfrak{X} \) it satisfies
-
(i)
\(d_{s}(p,v)=0\) iff \(p=v\);
-
(ii)
\(d_{s}(p,v)=d_{s}(v,p)\);
-
(iii)
\(d_{s}(p,t)\leq s(p,v)d_{s}(p,v)+ s(v,t)d_{s}(v,t)\).
The pair \((\mathfrak{X},d_{s})\) is then called a controlled metric-type space.
Remark 2.12
If for all \(p,q \in \mathfrak{X}, s(p,q)=b\) for some \(b \geq 1\), then Definition 2.11 coincides with the definition of a b-metric space.
Theorem 2.13
([1])
Let \((\mathfrak{X},d_{s})\) be a complete controlled metric-type space where \(d_{s}\) is continuous. Let \(\digamma:\mathfrak{X} \to \mathfrak{X}\) be a given mapping such that
where \(\kappa \in [0,1)\), and for each \(p_{0} \in \mathfrak{X}\)
where \(p_{i} =T^{i}{p_{0}}\). In addition, assume that for every \(x\in \mathfrak{X}\), we have
Then, Ϝ has a unique fixed point ϱ and for each \(y \in \mathfrak{X}\), \(\digamma ^{k} y \to \varrho \).
Now, we want to recall the definitions of generalized α-admissible, α-regular, and generalized Reich-type mappings in the setting of cone b-metric spaces over a Banach algebra.
Definition 2.14
([27])
Let \((\mathfrak{X},d_{b})\) be a cone b-metric space over a Banach algebra \(\mathcal{A}\) with \(\mathcal{K}\) an underlying solid cone. Let \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0,\infty ) \) and \(\digamma:\mathfrak{X} \to \mathfrak{X}\) be given mappings. Then,
-
(i)
Ϝ is said to be a generalized α-admissible mapping if for all \(p,q \in \mathfrak{X}, \alpha (p,q) \geq b\) implies that \(\alpha (\digamma p,\digamma q)\geq b\);
-
(ii)
\((\mathfrak{X},d_{b})\) is said to be α-regular if for every sequence \(\{u_{k}\}\in \mathfrak{X}\) with \(\alpha (u_{k},u_{k+1})\geq b \) for all \(k\in \mathbb{N}\) so that \(u_{k} \to p\), \(\alpha (u_{k},p)\geq b\).
Definition 2.15
([27])
Let \((\mathfrak{X},d_{b})\) be a cone b-metric space over a Banach algebra \(\mathcal{A}\) with coefficient b, \(\mathcal{K}\) an underlying solid cone, and \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0,\infty ) \) be a function. Then, a mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is called a generalized Reich-type contraction if there exist \(v_{1}, v_{2}, v_{3} \in \mathcal{K}\) such that for all \(p,q \in \mathfrak{X}\) with \(\alpha (p,q)\geq b\),
-
(i)
\(2b r(v_{1})+(b+1)r(v_{2} +v_{3}) <2\);
-
(ii)
\(d(\digamma p,\digamma q) \preceq v_{1} d(p,q)+v_{2} d(p,\digamma p)+v_{3} d(q,\digamma q)\).
3 Main results
In the following, we introduce a new type of metric space over a real Banach algebra that is called a controlled cone metric-type space over a Banach algebra. Using such spaces we prove some fixed-point theorems for generalized Reich-type contractions and generalized Lipschitz mappings. Our results extend and generalize some previous well-known results in the literature.
Definition 3.1
Let \(\mathcal{A}\) be a real Banach algebra with cone \(\mathcal{K}\), \(\mathfrak{X}\) be a nonempty set, and \(s: \mathfrak{X} \times \mathfrak{X} \to [1,\infty )\) be a function. A controlled cone metric type on \(\mathfrak{X}\) over a Banach algebra \(\mathcal{A}\) is a mapping \(d_{s}:\mathfrak{X} \times \mathfrak{X} \to \mathcal{A} \) such that
- \((E_{1})\):
-
\(d_{s}(p,q) \succeq \theta \) for all \(p,q \in \mathfrak{X}\) and \(d_{s}(p,q)=\theta \) iff \(p=q\);
- \((E_{2})\):
-
\(d_{s}(p,q)=d_{s}(q,p)\) for all \(p,q \in \mathfrak{X}\);
- \((E_{3})\):
-
\(d_{s}(p,v)\preceq s(p,q)d_{s}(p,q)+s(q,v) d_{s}(q,v)\) for all \(p,q,v \in \mathfrak{X}\).
The pair \((\mathfrak{X},d_{s})\) is then called a controlled cone metric-type space over a Banach algebra \(\mathcal{A}\).
Remark 3.2
It is clear that the class of controlled cone metric-type spaces over Banach algebra \(\mathcal{A}\) is larger than the classes of b-metric spaces and metric spaces over Banach algebras.
The definition of Cauchy sequences, convergent sequences, and completeness for a controlled cone metric-type space over a Banach algebra are the same as cone b-metric spaces over a Banach algebra defined in Definition 2.9.
In general, \(d_{s}\) is not necessarily a continuous function, but in this paper \(d_{s}\) will always mean a continuous function \(d_{s}:\mathfrak{X} \times \mathfrak{X} \to \mathcal{A}\).
Example 3.3
Let \(\mathfrak{X}=\{1,2,3\}\) and \(s: \mathfrak{X} \times \mathfrak{X} \to [1,\infty )\) be defined as \(s(p,q)=1+p+q\). Consider the real Banach algebra \(\mathcal{A}=\mathbb{R}^{2}\) with solid cone \(\mathcal{K}=\{(a,b)\in \mathbb{R}^{2}: a, b \geq 0\}\). Assume that we define \(d_{s}:\mathfrak{X} \times \mathfrak{X} \to \mathcal{A}\) by
Clearly, the first and second conditions of a controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) are satisfied. For the third condition, we have
Hence, for all \(p,q,v \in \mathfrak{X}\),
Thus, \((\mathfrak{X},d_{s})\) is a controlled cone metric-type space over a Banach algebra \(\mathcal{A}=\mathbb{R}^{2}\).
Remark 3.4
Let \((\mathfrak{X},d_{s})\) be a controlled cone metric-type space over Banach algebra \(\mathcal{A}\) with \(s: \mathfrak{X} \times \mathfrak{X} \to [1,\infty )\). If \(\mathcal{A}=\mathbb{R}\) and \(\mathcal{K}=[0,\infty )\), then \((\mathfrak{X},d_{s})\) is a controlled metric-type space.
We now define a generalized α-admissible mapping and an α-regular space in terms of controlled cone metric-type spaces over Banach algebras.
Definition 3.5
Consider a controlled cone metric space \((\mathfrak{X},d_{s})\) over a Banach algebra \(\mathcal{A}\) and \(\mathcal{K}\) an underlying solid cone in \(\mathcal{A}\). Let \(\digamma:\mathfrak{X} \to \mathfrak{X}\) and \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0,\infty )\) be mappings. Then,
-
(i)
Ϝ is said to be a generalized α-admissible mapping if for \(p,q \in \mathfrak{X}, \alpha (p,q) \geq s(p,q)\) implies that \(\alpha (\digamma p,\digamma q)\geq s(\digamma p,\digamma q)\);
-
(ii)
\((\mathfrak{X},d_{s})\) is said to be α-regular if for every sequence \(\{u_{k}\}\in \mathfrak{X}\) with \(\alpha (u_{k},u_{k+1})\geq s(u_{k},u_{k+1}) \) for all \(k\in \mathbb{N}\) so that \(u_{k} \to q\), \(\alpha (u_{k},q)\geq s(u_{k},q)\).
We are now able to define a generalized Reich-type contraction in the setting of controlled cone metric-type spaces over a Banach algebra.
Definition 3.6
Let \((\mathfrak{X},d_{s})\) be a controlled cone metric-type space over Banach algebra \(\mathcal{A}\) with \(\mathcal{K}\) an underlying solid cone and \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0,\infty )\) be a function. Then, a mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is called a generalized Reich-type contraction if there exist three vectors \(v_{1}, v_{2}, v_{3}\) in \(\mathcal{K}\) such that for all \(p,q \in \mathfrak{X}\) with \(\alpha (p,q)\geq s(p,q)\),
-
(i)
\(2s(p,q)r(v_{1})+(s(p,q)+1)r(v_{2} +v_{3}) <2\) and for each \(u_{0} \in \mathfrak{X}\) with \(u_{m}=\digamma ^{m}u_{0}\),
$$\begin{aligned} \lim_{m,i\to \infty} \frac{s(u_{i+1},u_{i+2})}{s(u_{i},u_{i+1})} s(u_{i+1},u_{m}) < \frac{1}{ \Vert \kappa \Vert }, \end{aligned}$$where \(\kappa = (2e-v)^{-1}(2v_{1} +v) \text{for} v=v_{2} + v_{3} \);
-
(ii)
\(d_{s}(\digamma p,\digamma q) \preceq v_{1} d_{s}(p,q)+v_{2} d_{s}(p, \digamma p)+v_{3} d_{s}(q,\digamma q)\).
The main result of our paper is given as follows:
Theorem 3.7
Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) with \(\mathcal{K}\) an underlying solid cone and \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0, \infty ) \) a mapping. Suppose that the mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is a generalized Reich-type contraction with vectors \(v_{1}, v_{2}, v_{3} \in \mathcal{K}\) such that
-
1.
Ϝ is a generalized α-admissible mapping;
-
2.
there exists \(u_{0} \in \mathfrak{X}\) such that \(\alpha (u_{0},\digamma u_{0})\geq s(u_{0},\digamma u_{0}) \);
-
3.
\((\mathfrak{X},d_{s})\) is regular or Ϝ is continuous.
Then, there exists a point ϱ in \(\mathfrak{X}\) that is fixed under the mapping Ϝ.
Proof
Let \(u_{0}\) be a point in \(\mathfrak{X}\) such that \(\alpha (u_{0},\digamma u_{0})\geq s(u_{0},\digamma u_{0})\). For \(u_{0}\in \mathfrak{X}\), if we define \(u_{1}=\digamma u_{0}, u_{2}=\digamma u_{1}=\digamma (\digamma u_{0})= \digamma ^{2}u_{0}, \ldots, u_{n+1}=\digamma u_{n} = \digamma ^{n+1}u_{0}\), then
However, Ϝ is generalized α-admissible and thus
and so by induction we obtain
By Definition 3.6, we have
that is,
Similarly,
i.e.,
Adding (3.1) and (3.2), we obtain
If we take \(v=v_{2} + v_{3}\), then we obtain
Note that
Hence, \(r(v)<1<2 \) and \(r(v)<2\). Thus, by Lemma 2.1, we deduce that \(2e-v\) is invertible and \((2e-v)^{-1}=\sum_{n=0}^{\infty} \frac{v^{n}}{2^{n+1}}, r((2e-v)^{-1})< \frac{1}{2-r(v)}\).
Thus, (3.3) becomes
where \(\kappa = (2e-v)^{-1} (2v_{1} +v)\). The inequality (3.4) implies that for all \(n \in \mathbb{N}\)
Now, if we take \(m>n\), then by (3.5), Definition 3.1 and \((E_{3})\), we have
In the above steps, we use the fact that \(s(p,q)\geq 1\) and thus \(x \preceq s(p,q)x \) for any \(x \in \mathcal{A}\). Let
Since by Definition 3.6, \(\Vert \kappa \Vert \lim_{m,i\to \infty} \frac{s(u_{i+1},u_{i+2})}{s(u_{i},u_{i+1})} s(u_{i+1},u_{m}) <1\), the series S converges absolutely. Using the ratio test, we have
However, \(\mathcal{A}\) is a Banach algebra and the series S is absolutely convergent and so converges in \(\mathcal{A}\). Thus, \(S_{m-1}-S_{n}= [ \sum_{i=n}^{m-1} ( \prod_{j=0}^{i} s(u_{j},u_{m}) )s(u_{i},u_{i+1}) \kappa ^{i} ]\to \theta \) as \(n,m \to \infty \) and so is \(d_{s}(u_{0},u_{1})(S_{m-1}-S_{n})\). Hence, by Lemma 2.5, for every \(c\gg \theta \), there exists a natural number \(n_{0}\) such that for all \(n\geq n_{0}, d_{s}(u_{n},u_{m})\ll c\). Thus, by Definition 2.9, \(\{u_{n}\}\) is a Cauchy sequence in \(\mathfrak{X}\). However, \(\mathfrak{X}\) is complete and so there exists \(\varrho \in \mathfrak{X}\) such that \(u_{n} \to \varrho \) as \(n \to \infty \).
We show that ϱ is fixed under the mapping Ϝ.
Suppose that Ϝ is continuous. It follows that \(u_{n+1}=\digamma u_{n} \to \digamma \varrho \) as \(n\to \infty \). However,the limit of a sequence is unique and so we have \(\digamma \varrho =\varrho \). Hence, ϱ is fixed under the mapping Ϝ in this case.
However, if \((\mathfrak{X},d_{s})\) is α-regular, then by Definition 3.5, we obtain
and
which further implies that
Similarly,
which further implies that
Therefore, by adding (3.6) and (3.7), we obtain
i.e.,
We also note by Definition 3.6 that
i.e., \(r(s(u_{n+1},\digamma \varrho ) v)<1<2\). Thus, by Lemma 2.1, \(2e-s(u_{n+1},\digamma \varrho )v\) is invertible and so (3.8) implies that
By Remark 2.10, the sequences \(\{d_{s}(u_{n+1},\varrho )\}\) and \(\{d_{s}(u_{n},\varrho )\}\) are c-sequences. Hence, by Lemma 2.4, the sequence \(\{\tau _{1} d_{s}(u_{n+1},\varrho ) +\tau _{2} d_{s}(u_{n},\varrho ) \}\) is a c-sequence (where \(\tau _{1} = (2e-s(u_{n+1}, \digamma \varrho )v)^{-1} s(\varrho, u_{n+1})(2e +s(u_{n+1}, \digamma \varrho )v)\) and \(\tau _{2} =(2e-s(u_{n+1}, \digamma \varrho )v)^{-1} s(\varrho, \digamma \varrho ) (2v_{1} +s(\varrho, \digamma \varrho )v)\)). Therefore, for any \(c \in \mathcal{A}\) with \(c\gg \theta \), there exists \(n_{0} \in \mathbb{N}\) such that
which further implies by Lemma 2.5 that \(d_{s}(\varrho, \digamma \varrho )=\theta \). Therefore, \(\digamma \varrho =\varrho \) and this completes the proof. □
Example 3.8
Let \(\mathcal{A}=C_{\mathbb{R}}^{1}[0,1]\) and \(\Vert f\Vert =\Vert f\Vert _{\infty}+\Vert f^{\prime }\Vert _{\infty}\). If we define point-wise multiplication of functions on \(\mathcal{A}\), then \(\mathcal{A}\) becomes a real Banach algebra with identity \(e(t)=1\). If we take \(\mathcal{K}=\{f\in \mathcal{A}: f(t)\geq 0, t \in [0,1]\}\), then \(\mathcal{K}\) is a nonnormal cone (see [28]). Let \(\mathfrak{X}=[0,\infty )\) and \(s:\mathfrak{X} \times \mathfrak{X} \to [1, \infty )\) be defined as \(s(p,q)=2+p+q\). Define \(d_{s}:\mathfrak{X} \times \mathfrak{X} \to \mathcal{A}\) by
Then, \(d_{s}\) is a controlled-type cone metric over \(\mathcal{A}\). Also, note that \(\mathfrak{X}\) is complete with respect to \(d_{s}\). We define \(\alpha:\mathfrak{X} \times \mathfrak{X} \to [0, \infty ) \) and \(\digamma:\mathfrak{X} \to \mathfrak{X}\) by
and
Note that for every \(p \in [0,1]\), \(\digamma p \in [0,1]\). Choosing \(v_{1}(t)=\frac{1}{9}+\frac{1}{9}t\), \(v_{2}(t)=\frac{1}{18}+\frac{1}{18}t\) and \(v_{3}(t)=\frac{1}{24}+\frac{1}{24}t\), we obtain that \(r(v_{1})=\frac{2}{9}\), \(r(v)=r(v_{2}+v_{3})=\frac{7}{36}\). Simple calculations show that \(2(2)r(v_{1})+(2+1)r(v)=\frac{53}{36}\) and so Ϝ is a generalized Reich-type contraction as
which further implies that \(2s(p,q) r(v_{1})+(s(p,q)+1)r(v) \leq \frac{53}{36} <2\). Also,
and
Similarly, by a simple calculation, one can show that
Next, we show that there is a point \(u_{0}\) in \(\mathfrak{X}\) such that \(\alpha (u_{0}, \digamma u_{0})\geq s(u_{0}, \digamma u_{0})\). Indeed, for \(u_{0}=1\), we have
Next, we show that Ϝ is a generalized α-admissible mapping. In fact, if \(p,q \in \mathfrak{X}\) are such that \(\alpha (p,q)\geq s(p,q)\), then by definition of α, \(p,q \in [0,1]\). Therefore, \(\digamma p, \digamma q \in [0,1]\) and so
Finally, we show that \((\mathfrak{X},d_{s})\) is α-regular. If we assume that a sequence \(\{p_{n}\}\) in \(\mathfrak{X}\) such that \(\alpha (p_{n}, p_{n+1}) \geq s(p_{n}, p_{n+1})\) for all \(n \in \mathbb{N}\) and \(p_{n} \to q \in \mathfrak{X}\) (as \(n \to \infty \)), then \(\{p_{n}\} \subseteq [0,1]\). However, \([0,1]\) is closed and so \(q \in [0,1]\). This implies that \(\alpha (p_{n}, q) \geq s(p_{n}, q)\) for all \(n \in \mathbb{N}\). Hence, all the conditions of Theorem 3.7 are satisfied and so Ϝ has a fixed point \(\varrho =0\).
Theorem 3.9
Let \(\mathcal{A}\) be a Banach algebra and \(\mathcal{K}\) be a solid cone in \(\mathcal{A}\). Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over \(\mathcal{A}\) and \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0, \infty ) \) be a function. Suppose that the mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is a generalized Reich-type contraction with vectors \(v_{1}, v_{2}, v_{3}\) in \(\mathcal{K}\) such that \(v_{1}\) commutes with \(v_{2} +v_{3}\) and
-
1.
Ϝ is a generalized α-admissible;
-
2.
there exists \(u_{0} \in \mathfrak{X}\) such that \(\alpha (u_{0},\digamma u_{0})\geq s(u_{0},\digamma u_{0})\);
-
3.
Ϝ is continuous or \((\mathfrak{X},d_{s})\) is regular;
-
4.
for any two fixed points \(\varpi, \zeta \) of Ϝ, there exists \(z \in \mathfrak{X}\) such that \(\alpha (\varpi, z)\geq s(\varpi, z)\) and \(\alpha (\zeta, z) \geq s(\zeta, z)\).
Then, there exists a unique point ϱ in \(\mathfrak{X}\) that is fixed under the mapping Ϝ.
Proof
Using Theorem 3.7 and the first three given conditions, we can say that there exists a point \(\varrho \in \mathfrak{X}\) that is fixed under the mapping Ϝ. We show that this point is unique and for this, let \(\zeta \in \mathrm{Fix}(\digamma )\) such that \(\varrho \ne \zeta \). Then, by Condition 4, there exists \(z \in \mathfrak{X}\) such that
Since Ϝ is a generalized α-admissible mapping and \(\varrho, \zeta \in \mathrm{Fix}(\digamma )\), by (3.10), we obtain
By Definition 3.6 and (3.11), we obtain
which further implies that
Similarly,
which further implies that
Adding (3.12) and (3.13), we have
i.e.,
Note that
Thus, \(r(s(\varrho, \digamma ^{i}z)v)<1<2\) and by Lemma 2.1, we can say that \(2e-s(\varrho, \digamma ^{i}z)v\) is invertible and \((2e-s(\varrho, \digamma ^{i}z)v)^{-1}=\sum_{n=0}^{\infty} \frac{(s(\varrho, \digamma ^{i}z)v)^{n}}{2^{n+1}}, r((2e-s(\varrho, \digamma ^{i}z)v)^{-1})<\frac{1}{2-r(s(\varrho, \digamma ^{i}z)v)}\). Thus, by (3.14), we have
i.e.,
where \(\tau = (2e - s(\varrho, \digamma ^{i}z) v)^{-1}(2v_{1} + s( \digamma ^{i-1}z, \varrho ) v)\). Therefore, we have
Since \(v_{1}\) commutes with \(v_{2} +v_{3} =v\),
which shows that \((2e-s(\varrho, \digamma ^{i}z)v)^{-1}\) commutes with \((2v_{1} +s(\digamma ^{i-1}z, \varrho )v)\). Hence, by Lemmas 2.1 and 2.2, we obtain
Then,
implies that
From Lemma 2.5, it follows that \(\Vert \tau ^{i}\Vert \to 0\) as \(i \to \infty \) and hence
By Remark 2.10, we conclude that for any \(c \in \mathcal{A}\) with \(c\gg \theta \), there exists \(N \in \mathbb{N} \) such that
Thus, by Lemma 2.5, \(\digamma ^{i}z \to \varrho \) as \(i \to \infty \). Similarly, we obtain that \(\digamma ^{i}z \to \zeta \) as \(i \to \infty \). Now, by uniqueness of limit, we conclude that \(\varrho = \zeta \), which completes the proof. □
Theorem 3.10
Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A} \) and \(\mathcal{K}\) be the associated cone in \(\mathcal{A}\). Let \(\digamma:\mathfrak{X} \to \mathfrak{X}\) be a mapping such that for all \(p,q\in \mathfrak{X}\),
where \(\kappa \in \mathcal{K}\) with \(r(\kappa )<1\) and for each \(p_{0} \in \mathfrak{X}\),
Then, there exists a unique point \(\varrho \in \mathfrak{X}\) that is fixed under the mapping Ϝ. Furthermore, for each \(u_{0}\in \mathfrak{X}\), the iterative sequence \(u_{n}=\digamma (u_{n-1})=\digamma ^{n}u_{0}\) converges to ϱ.
Proof
If we take \(v_{1}=\kappa \), \(v_{2}=v_{3}=\theta \) and \(\alpha (p,q) = s(p,q)\), then all the conditions of Theorem 3.7 are satisfied, i.e., Ϝ satisfies the condition of Definition 3.6. That is, Ϝ is generalized α-admissible, \((\mathfrak{X},d_{s}) \) is regular, and for every \(u_{0} \in \mathfrak{X}\), \(\alpha (u_{0},\digamma u_{0}) \succeq s(u_{0}, \digamma u_{0})\). Hence, there exists ϱ in \(\mathfrak{X}\) that is fixed under the mapping Ϝ. Now, it remains only to show that this fixed point is unique. Suppose that there is \(\zeta \in \mathfrak{X}\) such that \(\digamma \zeta =\zeta \). Then, we have
However, \(r(\kappa )<1\) and so by Lemma 2.1, \(e-\kappa \) is invertible. Thus, by Lemma 2.5\(d_{s}(\varrho,\zeta )=\theta \). □
Theorem 3.11
Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A} \) and \(\mathcal{K}\) be the associated cone in \(\mathcal{A}\). Suppose that \(\digamma:\mathfrak{X} \to \mathfrak{X}\) satisfies the generalized Lipschitz condition, i.e., for all \(p,q\in \mathfrak{X}\),
where \(\kappa \in \mathcal{K}\) with \(r(\kappa )<\frac {1}{s(p,q)+1}\) and for each \(p_{0} \in \mathfrak{X}\),
with \(\tau =(e-\kappa )^{-1}\kappa \). Then, there exists a unique point \(\varrho \in \mathfrak{X}\) that is fixed under the mapping Ϝ.
Proof
If we take \(v_{1}=\theta \), \(v_{2}=v_{3}=\kappa \) and \(\alpha (p,q) = s(p,q)\), then all the conditions of Theorem 3.7 are satisfied. Hence, there exists ϱ in \(\mathfrak{X}\) that is fixed under the mapping Ϝ. Finally, we show that ϱ is a unique fixed point of Ϝ. For this, if ζ is another fixed point of Ϝ, then
Therefore, \(\varrho =\zeta \). □
The following is the result of generalized Lipschitz mappings on cone b-metric spaces over a Banach algebra [15] that becomes a special case of Theorems 3.10 and 3.11 when we define \(s(p,q)=b\) for some \(b \geq 1\).
Theorem 3.12
([15])
Let \((\mathfrak{X},d)\) be a complete cone b-metric space over a Banach algebra \(\mathcal{A}\) with coefficient \(b\geq 1\) and \(\mathcal{K}\) be the associated solid cone (not necessarily normal) in \(\mathcal{A}\). Suppose that \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is a mapping such that for all \(p, q \in \mathfrak{X}\) one of the following conditions holds:
-
(i)
\(d(\digamma p, \digamma q)\preceq \kappa d(p,q)\) where \(\kappa \in \mathcal{K}\) with \(r(\kappa )< \frac {1}{b}\).
-
(ii)
\(d(\digamma p, \digamma q)\preceq \kappa (d(\digamma p,p)+d(\digamma q,q))\) where \(\kappa \in \mathcal{K}\) with \(r(\kappa )< \frac {1}{1+b}\).
Then, there exists a unique point \(\varrho \in \mathfrak{X} \) that is fixed under the mapping Ϝ.
Corollary 3.13
Let \((\mathfrak{X},d_{s})\) be a complete cone metric space over a Banach algebra \(\mathcal{A} \) and \(\mathcal{K}\) be the associated cone in \(\mathcal{A}\). Let \(\digamma:\mathfrak{X} \to \mathfrak{X}\) be a mapping such that for all \(p,q\in \mathfrak{X}\),
where \(\kappa \in \mathcal{K}\) with \(r(\kappa )<1\). Then, for each \(u_{0}\in \mathfrak{X}\), the iterative sequence \(u_{n}=\digamma (u_{n-1})=\digamma ^{n}u_{0}\) converges to a unique fixed point of Ϝ.
Proof
Taking \(b=1\) in Theorem 3.12, we obtain the required result. □
Remark 3.14
(i) If we take \(s(x,y)=b\) for some \(b\geq 1\) in Theorems 3.10 and 3.11, we obtain the main results of [15] for cone b-metric spaces over a Banach algebra.
(ii) By Remark 3.4, we obtain that Theorem 2.13 as a corollary of Theorem 3.10.
(iii) If we take \(s(x,y)=b\) for some \(b\geq 1\) in Theorems 3.7 and 3.9, we obtain the main results of [27] for cone b-metric spaces over a Banach algebra.
4 Consequences
In this section, we list some important consequences of our results that generalize Theorems 3.1, 3.2, and 3.4 in Hussain et al. [23], Theorems 3.1 and 3.2 in Xu and Radenovic [26], Theorems 3.1, 3.2, and 3.5 in Malhotra et al. [21], Theorems 3.1, 3.2, and 3.5 in Malhotra et al. [22], and Theorems 2.1 and 2.2 in Liu and Xu [14].
Definition 4.1
([20])
Let \(\mathfrak{X}\) be a nonempty set and \(\alpha: \mathfrak{X} \times \mathfrak{X} \to [0, \infty )\) be a function. A mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is said to be an α-admissible mapping if \(\alpha (p,q) \geq 1 \implies \alpha (\digamma p,\digamma q) \geq 1 \).
Definition 4.2
Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) and \(\mathcal{K}\) be the underlying solid cone. A mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is said to be a generalized α-Lipschitz contraction if for all \(p,q \in \mathfrak{X}\) with \(\alpha (p,q)\geq 1\),
where \(\kappa \in \mathcal{K}\) with \(r(\kappa ) < \frac{1}{s(p,q)}\) and for each \(p_{0} \in \mathfrak{X}\),
The following theorem becomes a special case of Theorem 3.7 if we define \(\alpha:\mathfrak{X} \times \mathfrak{X} \to [0,\infty )\) by \(\alpha (p,q) =s(p,q)\geq 1\) for all \(p,q \in \mathfrak{X}\) and take \(\kappa =v_{1}\), \(v_{2} =v_{3} =\theta \).
Theorem 4.3
Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) and \(\mathcal{K}\) be the associated solid cone. Suppose that \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is a generalized α-Lipschitz contraction with Lipschitz constant κ such that
-
(i)
Ϝ is α-admissible;
-
(ii)
there exists \(u_{0} \in \mathfrak{X}\) such that \(\alpha (u_{0},\digamma u_{0}) \geq 1\);
-
(iii)
Ϝ is continuous or if a sequence \(\{u_{n}\}\in \mathfrak{X}\) so that \(\alpha (u_{n},u_{n+1}) \geq 1 \) for all \(n\in \mathbb{N}\) and \(u_{n} \to q\) implies that \(\alpha (u_{n},q)\geq 1\) for all \(n \in \mathbb{N}\).
Then, there is a point ϱ in \(\mathfrak{X}\) that is fixed under Ϝ.
For the uniqueness of the fixed point, we use the following extra condition:
Theorem 4.4
If we add the condition (4.1) in the assumptions of Theorem 4.3, then the fixed point is unique.
Proof
The assertion follows simply from Theorems 4.3 and 3.9. □
Remark 4.5
(i) If we take \(s(p,q)=b\) for some \(b\geq 1\), then we obtain the main results of Hussain et al. [23, Theorems 3.1 and 3.2].
(ii) Theorems 3.1, 3.2, and 3.5 in Malhotra et al. [21] become special cases of Theorems 4.3 and 4.4, respectively, with \(s(x,y)=1, v_{1}=1\) and \(v_{2}=v_{3}=\theta \).
(iii) If we define \(s(p,q)=1\), \(v_{1}=\theta \) and \(v_{2}=v_{3}\), then Theorems 3.1, 3.2, and 3.3 in Malhotra et al. [22] become special cases of Theorems 4.3 and 4.4, respectively.
If the given controlled cone metric-type space \((\mathfrak{X},d_{s})\) over a Banach algebra \(\mathcal{A}\) is partially ordered, then we can use the following theorem.
Theorem 4.6
Let  be a partially ordered set and \(s: \mathfrak{X} \times \mathfrak{X} \to [1, \infty )\). Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) with underlying solid cone \(\mathcal{K}\). Assume that a nondecreasing mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) with respect to
be a partially ordered set and \(s: \mathfrak{X} \times \mathfrak{X} \to [1, \infty )\). Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) with underlying solid cone \(\mathcal{K}\). Assume that a nondecreasing mapping \(\digamma:\mathfrak{X} \to \mathfrak{X}\) with respect to  satisfies the following conditions:
satisfies the following conditions:
- \((1)\):
-
there exist vectors \(v_{1},v_{2}, v_{3} \in \mathcal{K}\) such that \(2s(p,q) r(v_{1})+(s(p,q)+1)r(v_{2} +v_{3}) <2\), \(d_{s}(\digamma p,\digamma q) \preceq v_{1} d_{s}(p,q)+v_{2} d_{s}(p, \digamma p)+v_{3} d_{s}(q,\digamma q)\) for all \(p,q \in \mathfrak{X}\) with
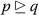 and for each \(p_{0} \in \mathfrak{X}\) with \(p_{n}=\digamma ^{n}p_{0}\), $$\begin{aligned} &\lim_{m,i\to \infty} \frac{s(p_{i+1},p_{i+2})}{s(p_{i},p_{i+1})} s(p_{i+1},p_{m}) < \frac{1}{ \Vert \kappa \Vert },\\ & \quad\textit{where } \kappa = (2e-v)^{-1}(2v_{1} +v) \textit{ for } v=v_{2} + v_{3}; \end{aligned}$$
and for each \(p_{0} \in \mathfrak{X}\) with \(p_{n}=\digamma ^{n}p_{0}\), $$\begin{aligned} &\lim_{m,i\to \infty} \frac{s(p_{i+1},p_{i+2})}{s(p_{i},p_{i+1})} s(p_{i+1},p_{m}) < \frac{1}{ \Vert \kappa \Vert },\\ & \quad\textit{where } \kappa = (2e-v)^{-1}(2v_{1} +v) \textit{ for } v=v_{2} + v_{3}; \end{aligned}$$ - \((2)\):
-
there exists \(u_{0} \in \mathfrak{X}\) such that
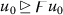 ;
; - \((3)\):
-
Ϝ is continuous or if \(\{u_{n}\}\) is a nondecreasing sequence in \(\mathfrak{X}\) with respect to
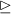 such that \(u_{n} \to q \in \mathfrak{X}\) as \((n \to \infty )\), then
such that \(u_{n} \to q \in \mathfrak{X}\) as \((n \to \infty )\), then 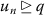 for all \(n \in \mathbb{N}\).
for all \(n \in \mathbb{N}\).
Then, there exists a point ζ in \(\mathfrak{X}\) that is fixed under the mapping Ϝ.
Proof
Define a function \(\alpha:\mathfrak{X} \times \mathfrak{X} \to [0, \infty )\) by

Then, Ϝ is a generalized Reich-type contraction by Condition (1). Now, since Ϝ is a nondecreasing mapping, Ϝ is a generalized α-admissible mapping. Condition (2) implies that there exists \(u_{0} \in \mathfrak{X}\) such that \(\alpha (u_{0},\digamma u_{0})=s(u_{0},\digamma u_{0})\). By Condition (3), we can see that either Ϝ is continuous or \((\mathfrak{X},d_{s})\) is regular. It follows that all the conditions of Theorem 3.7 are satisfied and so we conclude that there exists a point in \(\mathfrak{X}\) that is fixed under the mapping Ϝ. □
Corollary 4.7
Let  be a partially ordered set and \(s: \mathfrak{X} \times \mathfrak{X} \to [1, \infty )\). Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) with underlying solid cone \(\mathcal{K}\). Suppose \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is a nondecreasing mapping with respect to
be a partially ordered set and \(s: \mathfrak{X} \times \mathfrak{X} \to [1, \infty )\). Let \((\mathfrak{X},d_{s})\) be a complete controlled cone metric-type space over a Banach algebra \(\mathcal{A}\) with underlying solid cone \(\mathcal{K}\). Suppose \(\digamma:\mathfrak{X} \to \mathfrak{X}\) is a nondecreasing mapping with respect to  and the following assumptions hold:
and the following assumptions hold:
- \((1)\):
-
there exists \(\kappa \in \mathcal{K}\) with \(r(\kappa )< \frac{1}{s(p,q)}\) so that \(d_{s}(\digamma p,\digamma q) \preceq \kappa d_{s}(p,q)\) for all \(p,q \in \mathfrak{X}\) with
 and for each \(p_{0} \in \mathfrak{X}\) with \(p_{n}=\digamma ^{n}p_{0}\), $$\begin{aligned} \lim_{m,i\to \infty} \frac{s(p_{i+1},p_{i+2})}{s(p_{i},p_{i+1})} s(p_{i+1},p_{m})< \frac{1}{ \Vert \kappa \Vert }; \end{aligned}$$
and for each \(p_{0} \in \mathfrak{X}\) with \(p_{n}=\digamma ^{n}p_{0}\), $$\begin{aligned} \lim_{m,i\to \infty} \frac{s(p_{i+1},p_{i+2})}{s(p_{i},p_{i+1})} s(p_{i+1},p_{m})< \frac{1}{ \Vert \kappa \Vert }; \end{aligned}$$ - \((2)\):
-
there exists \(u_{0} \in \mathfrak{X}\) such that
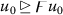 ;
; - \((3)\):
-
T is continuous or if \(\{u_{n}\}\) is a nondecreasing sequence in \(\mathfrak{X}\) with respect to
 such that \(u_{n} \to q \in \mathfrak{X}\) as \((n \to \infty )\), then
such that \(u_{n} \to q \in \mathfrak{X}\) as \((n \to \infty )\), then 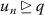 for all \(n \in \mathbb{N}\).
for all \(n \in \mathbb{N}\).
Then, there exists a unique point ϱ in \(\mathfrak{X}\) that is fixed under the mapping Ϝ.
Proof
The assertion follows directly, from Theorem 4.6 if we take \(v_{1}=\kappa \) and \(v_{2}=v_{3}=\theta \). □
Remark 4.8
(i) Theorem 4.6 becomes [27, Theorem 3.6] if we take \(s(p,q)=b\) for some \(b\geq 1\).
(ii) If we take \(s(p,q)=b\) for some \(b\geq 1\) in Corollary 4.7, then we obtain Theorems 4.2 and 4.3 of Hussain et al. [23].
(iii) Theorems 2.1 and 2.2 in Nieto and Rodreguez-Lopez [29] are special cases of Corollary 4.7 with \(s(p,q)=1\) and \(\mathcal{A}=\mathbb{R}\).
5 Conclusion
In this article, we introduced a new geometrical structure that is the hybrid of a cone metric space over Banach algebra and a controlled metric-type space. We have defined a metric space and we proved analogs of Banach-, Kannan- and Reich-type fixed-point theorems. We also furnished various concrete examples to establish the validity of our results. The obtained results generalize many well-known results in the literature.
Availability of data and materials
Not applicable.
References
Mlaiki, N., Aydi, H., Souayah, N., Abdeljawad, T.: Controlled metric type spaces and the related contraction principle. Mathematics 6, Article ID 194 (2018)
Czerwik, S.: Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1, 5–11 (1993)
Fernandez, J., Malviya, N., Mitrović, Z.D., Hussain, A., Parvaneh, V.: Some fixed point results on \(\mathcal{N}_{b}\)-cone metric spaces over Banach algebra. Adv. Differ. Equ. 2020, Article ID 529 (2020)
Fernandez, J., Malviya, N., Parvaneh, V., Aydi, H., Mohammadi, B.: On J-cone metric spaces over a Banach algebra and some fixed-point theorems. Adv. Math. Phys. 2021, Article ID 6620083 (2021)
Latif, A., Parvaneh, V., Salimi, P., Al-Mazrooei, A.E.: Various Suzuki type theorems in b-metric spaces. J. Nonlinear Sci. Appl. 8, 363–377 (2015)
Parvaneh, V., Hussain, N., Kadelburg, Z.: Generalized Wardowski type fixed point theorems via α-admissible FG-contractions in b-metric spaces. Acta Math. Sci. Ser. B Engl. Ed. 36, 1445–1456 (2016)
Kamran, T., Samreen, M., Ul Ain, A.: A generalization of b-metric space and some fixed point theorems. Mathematics 5, Article ID 19 (2017)
Abdeljawad, T., Mlaiki, N., Aydi, H., Souayah, N.: Double controlled metric type spaces and some fixed point results. Mathematics 6, Article ID 320 (2018)
Alamgir, N., Kiran, Q., Işık, H., Aydi, H.: Fixed point results via a Hausdorff controlled type metric. Adv. Differ. Equ. 2020, Article ID 24 (2020)
Lateef, D.: Fisher type fixed point results in controlled metric spaces. J. Math. Comput. Sci. 20, 234–240 (2020)
Huang, L.G., Zhang, X.: Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 332, 1468–1476 (2007)
Ercan, Z.: On the end of the cone metric spaces. Topol. Appl. 166, 10–14 (2014)
Du, W.S., Karapinar, E.: A note on cone b-metric and its related results: generalizations or equivalence. Fixed Point Theory Appl. 2013, Article ID 210 (2013)
Liu, H., Xu, S.: Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings. Fixed Point Theory Appl. 2013, Article ID 320 (2013)
Huang, H., Radenovic, S.: Some fixed point results of generalized Lipschitz mappings on cone b-metric spaces over Banach algebras. J. Comput. Anal. Appl. 20, 566–583 (2016)
Puiwong, J., Saejung, S.: Banach’s fixed point theorem, Ćirić’s and Kannan’s are equivalent via redefining the metric. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 114, Article ID 164 (2020)
Reich, S.: Some remarks concerning contraction mappings. Can. Math. Bull. 14, 121–124 (1971)
Dehici, A.: Common fixed point theorems for semigroup actions of Kannan’s type on strictly convex Banach spaces. J. Fixed Point Theory Appl. 20, Article ID 100 (2018)
Górnicki, J.: Various extensions of Kannan’s fixed point theorem. J. Fixed Point Theory Appl. 20, Article ID 20 (2018)
Samet, B., Vetro, C., Vetro, P.: Fixed point theorems for α-ψ-contractive type mappings. Nonlinear Anal. 75, 2154–2165 (2012)
Malhotra, S.K., Sharma, J.B., Shukla, S.: Fixed points of generalized α-admissible mappings in cone metric spaces with Banach algebra. Int. J. Anal. Appl. 9, 9–18 (2015)
Malhotra, S.K., Sharma, J.B., Shukla, S.: Fixed points of generalized Kannan type generalized α-admissible mappings in cone metric spaces with Banach algebra. Theory Appl. Math. Comput. Sci. 7, 1–13 (2017)
Hussain, N., Al-Solami, A.M., Kutbi, M.A.: Fixed points of generalized α-admissible mappings in cone b-metric spaces over Banach algebra. J. Math. Anal. 8, 89–97 (2017)
Rudin, W.: Functional Analysis. International Series in Pure and Applied Mathematics. McGraw-Hill, New York (1991)
Kadelburg, Z., Radenović, S.: A note on various types of cones and fixed point results in cone metric spaces. Asian J. Math. Appl. 2013, Article ID ama0104 (2013)
Xu, S., Radenović, S.: Fixed point theorems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality. Fixed Point Theory Appl. 2014, Article ID 102 (2014)
Vujaković, J., Auwalu, A., Sesum-Cacic, V.: Some new results for Reich type mappings on cone b-metric spaces over Banach algebras. Univ. Thought-Publ. Natural Sci. 8(2), 54–60 (2018)
Janković, S., Kadelburg, Z., Radenovic, S.: On cone metric spaces: a survey. Nonlinear Anal. 74, 2591–2601 (2011)
Nieto, J.J., Rodriguez-Lopez, R.: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 22(3), 223–239 (2005)
Acknowledgements
We would like to express our sincere gratitude to the anonymous referee for his/her helpful comments that helped to improve the quality of the manuscript.
Funding
The authors declare that there is no funding available for this paper.
Author information
Authors and Affiliations
Contributions
WU and HI carried out the mathematical studies, participated in their design and coordination, drafted the manuscript, and participated in the sequence alignment. NA, CP, and JRL participated in the design of the study and performed the mathematical and functional analysis. All the authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Human and animal rights
We would like to mention that this article does not contain any studies with animals and does not involve any studies with human beings.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ullah, W., Işık, H., Alam, N. et al. Continuous controlled cone metric-type spaces over real Banach algebras and fixed-point results. J Inequal Appl 2022, 52 (2022). https://doi.org/10.1186/s13660-022-02789-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-022-02789-x
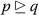 and for each
and for each 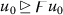 ;
;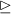 such that
such that 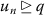 for all
for all  and for each
and for each 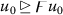 ;
; such that
such that 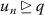 for all
for all