Ordering graphs with large eccentricity-based topological indices

Abstract

For a connected graph, the first Zagreb eccentricity index $\xi _{1}$ is defined as the sum of the squares of the eccentricities of all vertices, and the second Zagreb eccentricity index $\xi _{2}$ is defined as the sum of the products of the eccentricities of pairs of adjacent vertices. In this paper, we mainly present a different and universal approach to determine the upper bounds respectively on the Zagreb eccentricity indices of trees, unicyclic graphs and bicyclic graphs, and characterize these corresponding extremal graphs, which extend the ordering results of trees, unicyclic graphs and bicyclic graphs in (Du et al. in Croat. Chem. Acta 85:359–362, 2012; Qi et al. in Discrete Appl. Math. 233:166–174, 2017; Li and Zhang in Appl. Math. Comput. 352:180–187, 2019). Specifically, we determine the n-vertex trees with the i-th largest indices $\xi _{1}$ and $\xi _{2}$ for i up to $\lfloor n/2+1 \rfloor$ compared with the first three largest results of $\xi _{1}$ and $\xi _{2}$ in (Du et al. in Croat. Chem. Acta 85:359–362, 2012), the n-vertex unicyclic graphs with respectively the i-th and the j-th largest indices $\xi _{1}$ and $\xi _{2}$ for i up to $\lfloor n/2-1 \rfloor$ and j up to $\lfloor 2n/5+1 \rfloor$ compared with respectively the first two and the first three largest results of $\xi _{1}$ and $\xi _{2}$ in (Qi et al. in Discrete Appl. Math. 233:166–174, 2017), and the n-vertex bicyclic graphs with respectively the i-th and the j-th largest indices $\xi _{1}$ and $\xi _{2}$ for i up to $\lfloor n/2-2\rfloor$ and j up to $\lfloor 2n/15+1\rfloor$ compared with the first two largest results of $\xi _{2}$ in (Li and Zhang in Appl. Math. Comput. 352:180–187, 2019), where $n\ge 6$. More importantly, we propose two kinds of index functions for the eccentricity-based topological indices, which can yield more general extremal results simultaneously for some classes of indices. As applications, we obtain and extend some ordering results about the average eccentricity of bicyclic graphs, and the eccentric connectivity index of trees, unicyclic graphs and bicyclic graphs.

1 Introduction

Topological indices are numerical graph invariants that quantitatively characterize molecular structure, which are useful molecular descriptors that found considerable use in QSPR and QSAR studies [20, 21]. Several graph invariants based on vertex eccentricities have attracted much attention and have been subject to a large number of studies. We mainly study two kinds of eccentricity-based topological indices, that is, the first Zagreb eccentricity index and the second Zagreb eccentricity index, special cases of which have been studied due to their predictive capabilities for the physical and chemical properties of molecules.

All graphs considered in this paper are finite, simple, and connected. Let G be a graph with a vertex set $V(G)$ and an edge set $E(G)$. For $u\in V(G)$, $e_{G}(u)$ denotes the eccentricity of u in G, which is equal to the largest distance from u to other vertices of G.

The first Zagreb eccentricity index of G is defined as

$$ \xi _{1}(G)=\sum_{u\in V(G)}e^{2}_{G}(u), $$

while the second Zagreb eccentricity index of G is defined as

$$ \xi _{2}(G)=\sum_{uv\in E(G)}e_{G}(u)e_{G}(v). $$

These two types of Zagreb eccentricity indices were introduced by Vukičević and Graovac [22]. Some mathematical and computational properties of the Zagreb eccentricity indices have been obtained in [4, 6, 12, 13, 15, 16, 24]. Du et al. [6] determined the n-vertex trees with maximum, second-maximum, and third-maximum Zagreb eccentricity indices. Qi and Du [15] determined the trees with minimum Zagreb eccentricity indices when domination number, maximum degree, and bipartition size are respectively given, and they discussed the trees with maximum Zagreb eccentricity indices when domination number is given. Qi et al. [16] determined the n-vertex unicyclic graphs with maximum, second-maximum eccentricity index $\xi _{1}$, and maximum, second-maximum, and third-maximum eccentricity index $\xi _{2}$. Li and Zhang [12] determined the n-vertex bicyclic graphs with maximum and second-maximum eccentricity index $\xi _{2}$.

For a connected graph, the first Zagreb eccentricity index $\xi _{1}$ is defined as the sum of the squares of the eccentricities of all vertices, and the second Zagreb eccentricity index $\xi _{2}$ is defined as the sum of the products of the eccentricities of pairs of adjacent vertices. In this paper, we mainly present a different and universal approach to determine the upper bounds respectively on the Zagreb eccentricity indices of trees, unicyclic graphs and bicyclic graphs, and characterize these corresponding extremal graphs, which extend the ordering results of trees, unicyclic graphs, and bicyclic graphs in [6, 12, 16]. Specifically, we determine the n-vertex trees with the i-th largest indices $\xi _{1}$ and $\xi _{2}$ for i up to $\lfloor n/2+1 \rfloor$ compared with the first three largest results of $\xi _{1}$ and $\xi _{2}$ in [6], the n-vertex unicyclic graphs with respectively the i-th and the j-th largest indices $\xi _{1}$ and $\xi _{2}$ for i up to $\lfloor n/2-1 \rfloor$ and j up to $\lfloor 2n/5+1 \rfloor$ compared with respectively the first two and the first three largest results of $\xi _{1}$ and $\xi _{2}$ in [16], and the n-vertex bicyclic graphs with respectively the i-th and the j-th largest indices $\xi _{1}$ and $\xi _{2}$ for i up to $\lfloor n/2-2\rfloor$ and j up to $\lfloor 2n/15+1\rfloor$ compared with the first two largest results of $\xi _{2}$ in [12], where $n\ge 6$. More importantly, we propose two kinds of index functions for the eccentricity-based topological indices, which can yield more general extremal results simultaneously for some classes of indices. As applications, we obtain and extend some ordering results about the average eccentricity of bicyclic graphs and the eccentric connectivity index of trees, unicyclic graphs and bicyclic graphs.

2 Preliminaries

Let $n_{0}$ and $d_{0}$ be positive integers. Let $\mathbf{T}_{n_{\ge n_{0}}}$ (res. $\mathbf{U}_{n_{\ge n_{0}}}$, $\mathbf{B}_{n_{\ge n_{0}}}$) be the set of n-vertex trees (res. unicyclic graphs, bicyclic graphs), where $n\ge n_{0}$. Let $\mathbf{T}({n_{\ge n_{0}},d_{\le d_{0}}})$ (res. $\mathbf{U}({n_{\ge n_{0}},d_{\le d_{0}}})$, $\mathbf{B}({n_{\ge n_{0}},d_{\le d_{0}}})$) be the set of n-vertex trees (res. unicyclic graphs, bicyclic graphs) with the diameter d, where $n\ge n_{0}$ and $d\le d_{0}$.

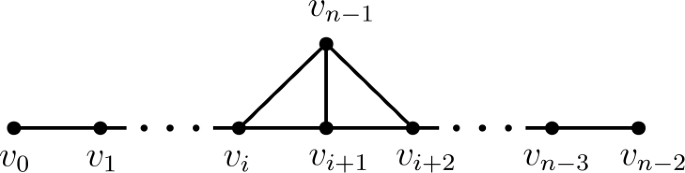
Let $P_{n}$ be the path on n vertices. For $2\le d\le n-1$, let $T^{(n,d)}=\{T_{n,d}^{a}:1\leq a\leq \lfloor (n+1-d)/2\rfloor \}$, where $T_{n,d}^{a}$ is the n-vertex tree obtained by attaching a and $n+1-a-d$ pendent vertices respectively to the two end vertices of the path $P_{d-1}$. For $n\geq 4$, let $T_{n}^{i}$ be the tree formed by attaching a pendent vertex $v_{n-1}$ to a vertex $v_{i}$ of the path $P_{n-1}=v_{0}v_{1}\cdots v_{n-2}$, where $1\le i\le \lfloor \frac{n-2}{2}\rfloor$ (see Fig. 1). In particular, $T^{0}_{n}=P_{n}$.

Figure 1

The graph $T_{n}^{i}$

The following observation is obvious.

Observation 2.1

If G is a connected graph such that $G-e$ is also connected for $e\in E(G)$, then $e_{G}(u)\le e_{G-e}(u)$ for $u\in V(G)$, and thus $\xi _{1}(G)\leq \xi _{1}(G-e)$.

Lemma 2.2

([6])

Let $G\in \mathbf{T}({n_{\ge 3},d_{\le n-1}})$. Then

$$\begin{aligned} \xi _{1}(G)\leq f_{1}(n,d),\qquad \xi _{2}(G)\leq f_{2}(n,d) \end{aligned}$$

with equality if and only if $G\in T^{(n,d)}$, where

$$\begin{aligned} &f_{1}(n,d)=\textstyle\begin{cases} d^{2}n-\frac{5d^{3}-2d}{12}& \textit{if }d\textit{ is even}, \\ d^{2}n-\frac{5d^{3}-5d}{12}& \textit{if }d\textit{ is odd}, \end{cases}\displaystyle \\ &f_{2}(n,d)=\textstyle\begin{cases} d(d-1)n-\frac{5d^{3}-8d}{12}& \textit{if }d\textit{ is even}, \\ d(d-1)n-\frac{5d^{3}-11d-6}{12}& \textit{if }d\textit{ is odd}, \end{cases}\displaystyle \end{aligned}$$

and $f_{1}(n,d)$ and $f_{2}(n,d)$ are increasing for $2\leq d\leq n-1$.

For $n\ge 3$ and $0\le i\le \lfloor \frac{n-3}{2}\rfloor$, let $P_{n,3}(i)$ be the n-vertex unicyclic graph formed by attaching two pendent paths with i and $n-3-i$ vertices respectively to the two vertices of a triangle (see Fig. 2). For $n\ge 4$ and $0\le i \le \lfloor \frac{n-4}{2}\rfloor$, let $P_{n,4}(i)$ be the n-vertex unicyclic graph formed by attaching two pendent paths with i and $n-4-i$ vertices respectively to the two non-adjacent vertices of a quadrangle (see Fig. 3). For $n\geq 4$ and $0\le i\le \lfloor \frac{n-4}{2}\rfloor$, let $B_{n}(i)$ be the n-vertex bicyclic graph formed by adding an edge between $v_{n-1}$ and $v_{i+1}$ in $P_{n,4}(i)$ (see Fig. 4).

Figure 2

The graph $P_{n,3}({i})$

Figure 3

The graph $P_{n,4}({i})$

Figure 4

The graph $B_{n}({i})$

Lemma 2.3

$(1)$ For $1\le i \le \lfloor \frac{n-4}{2}\rfloor$, $\xi _{1}(B_{n}(i-1))=\xi _{1}(P_{n,4}(i-1))=\xi _{1}(P_{n,3}(i))= \xi _{1}(T^{i+1}_{n})$ and $\xi _{1}(P_{n,3}(0))=\xi _{1}(T^{1}_{n})$;

$(2)$ For $1\le i \le \lfloor \frac{n-6}{2}\rfloor$, $\xi _{1}(P_{n,3}(i-1))> \xi _{1}(P_{n,3}(i))>\xi _{1}(P_{n,3}(i+1))$, $\xi _{1}(P_{n,4}(i-1))> \xi _{1}(P_{n,4}(i))$, and $\xi _{1}(B_{n}(i-1))> \xi _{1}(B_{n}(i))$;

$(3)$ For $1\le i \le \lfloor \frac{n-6}{2}\rfloor$, $\xi _{2}(P_{n,3}(i-1))>\xi _{2}(P_{n,4}(i-1))>\xi _{2}(P_{n,3}(i))> \xi _{2}(P_{n,4}(i))>\xi _{2}(P_{n,3}(i+1))$ and $\xi _{2}(B_{n}(i-1))> \xi _{2}(B_{n}(i))$.

Proof

Note that $P_{n,3}(i)$ (res. $P_{n,4}(i-1)$, $B_{n}(i-1)$) with $0\le i \le \lfloor \frac{n-4}{2}\rfloor$ (res. $1\le i \le \lfloor \frac{n-4}{2}\rfloor$) can be obtained from $T^{i+1}_{n}$ by adding an edge $v_{i}v_{n-1}$ (res. $v_{i}v_{n-1}$, two edges $v_{i}v_{n-1}$ and $v_{i-1}v_{n-1}$). From the above fact we may easily find that vertices in $P_{n,3}(i)$, $P_{n,4}(i-1)$, $B_{n}(i-1)$, and $T^{i+1}_{n}$ with the same label have equal eccentricity for $1\le i\le \lfloor \frac{n-4}{2}\rfloor$, and so do the vertices in $P_{n,3}(0)$ and $T^{1}_{n}$. Thus result $(1)$ follows.

Note that $e_{T^{i+1}_{n}}(v_{j})=e_{T^{i}_{n}}(v_{j})$ for $0\le j \le n-2$ and $e_{T^{i}_{n}}(v_{n-1})=n-1-i$ for $0\le i\le \lfloor \frac{n-2}{2}\rfloor$. Then, for $0\le i\le \lfloor \frac{n-4}{2}\rfloor$, we have $\xi _{1}(T^{i+1}_{n})<\xi _{1}(T^{i}_{n})$ and $\xi _{2}(T^{i+1}_{n})<\xi _{2}(T^{i}_{n})$. Thus, combining result $(1)$, we have result $(2)$ directly.

For $0\le i \le \lfloor \frac{n-4}{2}\rfloor$,

$$\begin{aligned} \xi _{2}\bigl(P_{n,3}(i)\bigr)=\xi _{2} \bigl(T_{n}^{i+1}\bigr)+(n-i-2)^{2}. \end{aligned}$$

For $1\le i \le \lfloor \frac{n-4}{2}\rfloor$,

$$\begin{aligned} \xi _{2}\bigl(P_{n,4}(i-1)\bigr)=\xi _{2} \bigl(T_{n}^{i+1}\bigr)+(n-i-1) (n-i-2). \end{aligned}$$

For $0\le i \le \lfloor \frac{n-6}{2}\rfloor$,

$$\begin{aligned} \xi _{2}\bigl(B_{n}(i)\bigr)=\xi _{2} \bigl(T_{n}^{i+2}\bigr)+(n-3-i) (2n-5-2i). \end{aligned}$$

Then, combining the fact that $\xi _{2}(T^{i+1}_{n})<\xi _{2}(T^{i}_{n})$, result $(3)$ follows easily. □

3 Main results of Zagreb eccentricity indices

3.1 Ordering trees with large Zagreb eccentricity indices

Theorem 3.1

Among the graphs in $\mathbf{T}_{n_{\ge 3}}$, $P_{n}$ for $n \geq 3$ is the unique graph with the largest eccentricity indices $\xi _{1}$ and $\xi _{2}$, and $T_{n}^{i}$ for $n\ge 4$ and $1\leq i \leq \lfloor n/2-1\rfloor$ is the unique graph with the $(i+1)$th largest eccentricity indices $\xi _{1}$ and $\xi _{2}$, where

$$\begin{aligned} &\xi _{1}(P_{n})=\textstyle\begin{cases} \frac{7n^{3}-9n^{2}+2n}{12}& \textit{if }n\textit{ is even}, \\ \frac{{7n}^{3}-9n^{2}-n+3}{12}& \textit{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\xi _{2}(P_{n})=\textstyle\begin{cases} \frac{7n^{3}-21n^{2}+20n}{12}& \textit{if }n\textit{ is even}, \\ \frac{{7n}^{3}-21n^{2}+17n-3}{12}& \textit{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\xi _{1}\bigl(T_{n}^{i}\bigr)=\textstyle\begin{cases} \frac{7n^{3}-30n^{2}+38n-12}{12}+(n-i-1)^{2}& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-30n^{2}+41n-18}{12}+(n-i-1)^{2}& \textit{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\xi _{2}\bigl(T_{n}^{i}\bigr)=\textstyle\begin{cases} \frac{7n^{3}-42n^{2}+80n-48}{12}+(n-i-1)(n-i-2)& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-42n^{2}+83n-48}{12}+(n-i-1)(n-i-2)& \textit{if }n\textit{ is odd}. \end{cases}\displaystyle \end{aligned}$$

Proof

Let $T\in \mathbf{T}({n_{\ge 3},d_{\le n-1}})$. If $n=3$ or $n=4$, then the result follows easily. Suppose that $n\ge 5$. Note that $f_{1}(n,d)$ and $f_{2}(n,d)$ are increasing for $2\le d\le n-1$ by Lemma 2.2. Then $\xi _{k}(T)\le f_{k}(n,d)\le f_{k}(n,n-3)< f_{k}(n,n-2)< f_{k}(n,n-1)$ for any $T\in \mathbf{T}({n_{\ge 5},d_{\le n-3}})$, where $k=1,2$. Note that $T^{(n,n-1)}=\{P_{n}\}$ and $T^{(n,n-2)}=\{T^{1}_{n}\}$. Then $P_{n}$ and $T^{1}_{n}$ for $n\ge 5$ are respectively the unique n-vertex trees with the largest and the second largest eccentricity indices $\xi _{1}$ and $\xi _{2}$.

Suppose that $2\leq i \leq \lfloor n/2-1\rfloor$. Among the graphs in $\mathbf{T}_{n_{\ge 3}}$, the $(i+1)$th largest eccentricity indices $\xi _{1}$ and $\xi _{2}$ are achieved by the trees in $\mathbf{T}(n_{\ge 5},d_{=n-2}) \setminus \{T_{n}^{j}:1\le j \le i-1 \}$ or in $T^{(n,n-3)}$ with the largest eccentricity indices $\xi _{1}$ and $\xi _{2}$.

Let $T_{1}\in \mathbf{T}(n_{\ge 5},d_{=n-2}) \setminus \{T_{n}^{j}:1\le j \le i-1\}$. Since $\xi _{1}(T_{n}^{i})<\xi _{1}(T_{n}^{i-1})$ and $\xi _{2}(T_{n}^{i})<\xi _{2}(T_{n}^{i-1})$, we have $\xi _{1}(T_{1})\le \xi _{1}(T_{n}^{i})$ and $\xi _{2}(T_{1})\le \xi _{2}(T_{n}^{i})$, where the equalities hold if and only if $T_{1}=T_{n}^{i}$. For $T_{2}\in T^{(n,n-3)}$, by direct calculation, we have

$$\begin{aligned} \xi _{1}\bigl(T_{n}^{\lfloor n/2-1\rfloor }\bigr)-\xi _{1}(T_{2}) &=\textstyle\begin{cases} 5n-11& \text{if }n\textit{ is even}, \\ 6n-12& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &>0, \\ \xi _{2}\bigl(T_{n}^{\lfloor n/2-1\rfloor }\bigr)-\xi _{2}(T_{2}) &=\textstyle\begin{cases} \frac{9n}{2}-13& \text{if }n\textit{ is even}, \\ \frac{11n-27}{2}& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &>0. \end{aligned}$$

Thus $T_{n}^{i}$ is the unique n-vertex tree with the $(i+1)$th largest eccentricity indices $\xi _{1}$ and $\xi _{2}$, where $1\leq i \leq \lfloor n/2-1\rfloor$. The result follows. □

In fact, from the proof of Theorem 3.1, we have the following corollary easily.

Corollary 3.2

Among the graphs in $\mathbf{T}_{n_{\ge 3}}$, $T^{(n,n-3)}$ is the set of graphs with the $\lfloor n/2+1\rfloor$th largest eccentricity indices $\xi _{1}$ and $\xi _{2}$, and $f_{k}(n,n-3)<\xi _{k}(T^{\lfloor \frac{n-2}{2}\rfloor }_{n})$ for $k=1,2$.

3.2 Ordering unicyclic graphs with large Zagreb eccentricity indices

Lemma 3.3

Let $G\in \mathbf{U}(n_{\ge 6},d_{=n-2}) \setminus (\{P_{n,3}(i):0 \le i\le \lfloor \frac{n-4}{2}\rfloor \}\cup \{P_{n,4}(i):0\le i\le \lfloor \frac{n-6}{2}\rfloor \} )$. Then $\xi _{k}(G)<\xi _{k}(P_{n,3}(\lfloor \frac{n-4}{2}\rfloor ))$ for $k=1,2$.

Proof

If n is even, then $G=P_{n,4}(\frac{n-4}{2})$. If n is odd, then $G\in \{P_{n,3}(\frac{n-3}{2}),P_{n,4}(\frac{n-5}{2})\}$. By direct computation, we have

$$\begin{aligned} \xi _{1} \biggl(P_{n,4}\biggl(\biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr)-\xi _{1} \biggl(P_{n,3}\biggl(\biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr) &= \biggl\lceil \frac{n-2}{2} \biggr\rceil ^{2}- \biggl\lceil \frac{n}{2} \biggr\rceil ^{2}< 0, \\ \xi _{2} \biggl(P_{n,4}\biggl(\biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr)-\xi _{2} \biggl(P_{n,3}\biggl(\biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr) &=\textstyle\begin{cases} -\frac{n}{2}& \text{if }n\textit{ is even}, \\ -n& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &< 0, \end{aligned}$$

and for odd n,

$$\begin{aligned} &\xi _{1} \biggl(P_{n,3}\biggl(\frac{n-3}{2}\biggr) \biggr)-\xi _{1} \biggl(P_{n,3}\biggl( \frac{n-5}{2} \biggr) \biggr)= \biggl(\frac{n-1}{2} \biggr)^{2}- \biggl( \frac{n+1}{2} \biggr)^{2}< 0, \\ &\xi _{2} \biggl(P_{n,3}\biggl(\frac{n-3}{2}\biggr) \biggr)-\xi _{2} \biggl(P_{n,3}\biggl( \frac{n-5}{2} \biggr) \biggr)=\frac{-3n+1}{2}< 0. \end{aligned}$$

Thus the result follows. □

Theorem 3.4

Among the graphs in $\mathbf{U}_{n_{\ge 6}}$, $P_{n,3}(0)$ is the unique graph with the largest eccentricity index $\xi _{1}$, and $P_{n,3}(i)$ and $P_{n,4}(i-1)$ with $1\le i \le \lfloor \frac{n-4}{2}\rfloor$ are the graphs with the $(i+1)$th largest eccentricity index $\xi _{1}$, where

$$\begin{aligned} &\xi _{1}\bigl(P_{n,3}(0)\bigr) =\textstyle\begin{cases} \frac{7n^{3}-30n^{2}+38n-12}{12}+(n-2)^{2}& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-30n^{2}+41n-18}{12}+(n-2)^{2}& \textit{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\xi _{1}\bigl(P_{n,3}(i)\bigr)=\xi _{1} \bigl(P_{n,4}(i-1)\bigr) =\textstyle\begin{cases} \frac{7n^{3}-30n^{2}+38n-12}{12}+(n-i-2)^{2}& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-30n^{2}+41n-18}{12}+(n-i-2)^{2}& \textit{if }n\textit{ is odd}. \end{cases}\displaystyle \end{aligned}$$

Proof

Let $G\in \mathbf{U}(n_{\ge 6},d_{\le n-2})$. From Lemmas 2.3(2) and 3.3, we only need to show that $\xi _{1}(G)<\xi _{1}(P_{n,3}(\lfloor \frac{n-4}{2}\rfloor ))$ for $G\in \mathbf{U}(n_{\ge 6},d_{\le n-3})$.

It is easy to find that there exists an edge e on the cycle of G such that the diameter of $G-e$ is at most $n-3$. Note that $f_{1}(n,n-3)<\xi _{1}(T^{\lfloor \frac{n-2}{2}\rfloor }_{n})$ by Corollary 3.2. Then, by Observation 2.1 and Lemmas 2.2 and 2.3(1), we have

$$ \xi _{1}(G)\le \xi _{1}(G-e)\le f_{1}(n,n-3)< \xi _{1} \bigl(T^{ \lfloor \frac{n-2}{2}\rfloor }_{n} \bigr) =\xi _{1} \biggl(P_{n,3}\biggl( \biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr). $$

Thus we have the result. □

Combining Lemmas 2.3(3) and 3.3, we have the following proposition.

Proposition 3.5

Among the graphs in $\mathbf{U}(n_{\ge 6},d_{=n-2})$, $P_{n,3}(i)$ with $0\le i \le \lfloor \frac{n-4}{2}\rfloor$ is the unique graph with the $(2i+1)$th largest eccentricity index $\xi _{2}$, and $P_{n,4}(i-1)$ with $1\le i \le \lfloor \frac{n-4}{2}\rfloor$ is the unique graph with the $(2i)$th largest eccentricity index $\xi _{2}$.

Theorem 3.6

Among the graphs in $\mathbf{U}_{n_{\ge 6}}$, $P_{n,3}(i)$ with $0\le i \le \lfloor \frac{n}{5}\rfloor$ is the unique graph with the $(2i+1)$th largest eccentricity index $\xi _{2}$, and $P_{n,4}(i-1)$ with $1\le i \le \lfloor \frac{n}{5}\rfloor$ is the unique graph with the $(2i)$th largest eccentricity index $\xi _{2}$, where

$$\begin{aligned} &\xi _{2}\bigl(P_{n,3}(i)\bigr) =\textstyle\begin{cases} \frac{7n^{3}-42n^{2}+80n-48}{12}+(2n-2i-5)(n-i-2)& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-42n^{2}+83n-48}{12}+(2n-2i-5)(n-i-2)& \textit{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\xi _{2}\bigl(P_{n,4}(i-1)\bigr) =\textstyle\begin{cases} \frac{7n^{3}-42n^{2}+80n-48}{12}+(2n-2i-4)(n-i-2)& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-42n^{2}+83n-48}{12}+(2n-2i-4)(n-i-2)& \textit{if }n\textit{ is odd}. \end{cases}\displaystyle \end{aligned}$$

Proof

Suppose that $G\in \mathbf{U}(n_{\ge 6},d_{\le n-2})$. By Proposition 3.5, we only need to show that $\xi _{2}(G)<\xi _{2}(P_{n,3}( \lfloor \frac{n}{5}\rfloor ))$ for $G\in \mathbf{U}(n_{\ge 6},d_{\le n-3})$.

Note that there exists an edge e such that $G-e$ is a spanning tree with the diameter at most $n-3$ and the maximum eccentricities of the two vertices on the edge e are $n-3$ and $n-3$. Then, by Observation 2.1 and Lemma 2.2, we have

$$ \xi _{2}(G)\le \xi _{2}(G-e)+(n-3) (n-3)\le f_{2}(n,n-3)+(n-3) (n-3). $$

Thus, by direct calculation, for $0\le i\le \frac{n}{5}$, we have

$$\begin{aligned} \xi _{2}\bigl(P_{n,3}(i)\bigr)-\xi _{2}(G) &\ge \textstyle\begin{cases} \frac{3n^{2}}{4}-(4i-2)n+2i^{2}+9i-12& \text{if }n\textit{ is even}, \\ \frac{3n^{2}}{4}-(4i-\frac{5}{2})n+2i^{2}+9i-\frac{49}{4}& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\ge \textstyle\begin{cases} \frac{3n^{2}}{100}+\frac{19n}{5}-12& \text{if }n\textit{ is even}, \\ \frac{3n^{2}}{100}+\frac{43n}{10}-\frac{49}{4}& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &>0, \end{aligned}$$

and the result follows. □

3.3 Ordering bicyclic graphs with large Zagreb eccentricity indices

Lemma 3.7

Let $G\in \mathbf{B}(n_{\ge 6},d_{=n-2}) \setminus \{B_{n}(i):0\le i\le \lfloor \frac{n-6}{2}\rfloor \}$. Then $\xi _{k}(G)<\xi _{k}(B_{n}(\lfloor \frac{n-6}{2}\rfloor ))$ for $k=1,2$.

Proof

If n is even, then $G=B_{n}(\frac{n-4}{2})$. If n is odd, then $G=B_{n}(\frac{n-5}{2})$. By direct computation, we have

$$\begin{aligned} \xi _{1} \biggl(B_{n}\biggl(\biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr)-\xi _{1} \biggl(B_{n}\biggl(\biggl\lfloor \frac{n-6}{2}\biggr\rfloor \biggr) \biggr) &= \biggl\lceil \frac{n-2}{2} \biggr\rceil ^{2}- \biggl\lceil \frac{n}{2} \biggr\rceil ^{2}< 0, \\ \xi _{2} \biggl(B_{n}\biggl(\biggl\lfloor \frac{n-4}{2}\biggr\rfloor \biggr) \biggr)-\xi _{2} \biggl(B_{n}\biggl(\biggl\lfloor \frac{n-6}{2}\biggr\rfloor \biggr) \biggr) &=\textstyle\begin{cases} -2n+1& \text{if }n\textit{ is even}, \\ -\frac{5n+1}{2}& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &< 0. \end{aligned}$$

Thus the result follows. □

Theorem 3.8

Among the graphs in $\mathbf{B}_{n_{\ge 6}}$, $B_{n}(i)$ with $0\le i\le \lfloor \frac{n-6}{2}\rfloor$ is the unique graph with the $(i+1)$th largest eccentricity index $\xi _{1}$, where

$$\begin{aligned} \xi _{1}\bigl(B_{n}(i)\bigr)=\textstyle\begin{cases} \frac{7n^{3}-30n^{2}+38n-12}{12}+(n-i-3)^{2}& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-30n^{2}+41n-18}{12}+(n-i-3)^{2}& \textit{if }n\textit{ is odd}. \end{cases}\displaystyle \end{aligned}$$

Proof

Suppose that $G\in \mathbf{B}(n_{\ge 6},d_{\le n-2})$. From Lemmas 2.3(2) and 3.7, we only need to show that $\xi _{1}(G)<\xi _{1}(B_{n}(\lfloor \frac{n-6}{2}\rfloor ))$ and $G\in \mathbf{B}(n_{\ge 6},d_{\le n-3})$.

It is easy to find that there exist two edges $e_{1}$ and $e_{2}$ on the cycle of G such that the diameter of $G-e_{1}-e_{2}$ is at most $n-3$. Note that $f_{1}(n,n-3)<\xi _{1}(T^{\lfloor \frac{n-2}{2}\rfloor }_{n})$ by Corollary 3.2. Then, by Observation 2.1 and Lemmas 2.2 and 2.3(1), we have

$$ \xi _{1}(G)\le \xi _{1}(G-e_{1}-e_{2}) \le f_{1}(n,n-3)< \xi _{1} \bigl(T^{ \lfloor \frac{n-2}{2}\rfloor }_{n} \bigr) =\xi _{1} \biggl(B_{n,2}\biggl( \biggl\lfloor \frac{n-6}{2}\biggr\rfloor \biggr) \biggr). $$

Thus the result follows. □

Combining Lemmas 2.3(3) and 3.3, we have the following proposition.

Proposition 3.9

Among the graphs in $\mathbf{B}(n_{\ge 6},d_{=n-2})$, $B_{n}(i)$ with $0\le i \le \lfloor \frac{n-6}{2}\rfloor$ is the unique graph with the $(i+1)$th largest eccentricity index $\xi _{2}$.

Theorem 3.10

Among all the graphs in $\mathbf{B}_{n_{\ge 6}}$, $B_{n}(i)$ is the $(i+1)$th largest eccentricity index $\xi _{2}$ with $0\le i \le \lfloor \frac{2n}{15} \rfloor$, where

$$\begin{aligned} \xi _{2}\bigl(B_{n}(i)\bigr)=\textstyle\begin{cases} \frac{7n^{3}-42n^{2}+80n-48}{12}+3(n-i-3)^{2}& \textit{if }n\textit{ is even}, \\ \frac{7n^{3}-42n^{2}+83n-48}{12}+3(n-i-3)^{2}& \textit{if }n\textit{ is odd}. \end{cases}\displaystyle \end{aligned}$$

Proof

Suppose that $G\in \mathbf{B}(n_{\ge 6},d_{\le n-2})$. Then, by Proposition 3.9, we only need to show that $\xi _{2}(G)<\xi _{2}(B_{n}(\lfloor \frac{2n}{15} \rfloor ))$ for $G\in \mathbf{B}(n_{\ge 6},d_{\le n-3})$.

Note that there exist two edges $e_{1},e_{2}$ on the cycle(s) such that $G-e_{1}-e_{2}$ is a spanning tree with the diameter at most $n-3$, and all the vertices incident to the edges $e_{1},e_{2}$ have eccentricities at most $n-3$. Then, by Observation 2.1 and Lemma 2.2, we have

$$ \xi _{2}(G)\le \xi _{2}(G-e_{1}-e_{2})+2(n-3)^{2} \le f_{2}(n,n-3)+2(n-3)^{2}. $$

Thus, for $0\le i\le \frac{2n}{15}$, we have

$$\begin{aligned} \xi _{2}\bigl(B_{n}(i)\bigr)-\xi _{2}(G)& \ge \textstyle\begin{cases} \frac{3n^{2}}{4}-(6i+1)n+3i^{2}+18i-4& \text{if }n\textit{ is even}, \\ \frac{3n^{2}}{4}-(6i+\frac{1}{2})n+3i^{2}+18i-\frac{17}{4}& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &\ge \textstyle\begin{cases} \frac{n^{2}}{300}+\frac{7n}{5}-4& \text{if }n\textit{ is even}, \\ \frac{n^{2}}{300}+\frac{19n}{10}-\frac{17}{4}& \text{if }n\textit{ is odd}, \end{cases}\displaystyle \\ &>0, \end{aligned}$$

and the result follows. □

4 Ordering graphs with large eccentricity-based topological indices

Most papers on this topic study just one topological index and find its extremal values (or perhaps several near-extreme values) over n-vertex trees or other simple classes. We propose studying such problems in terms of general properties of some index functions for the eccentricity-based topological indices. Requiring only the properties needed for the argument yields a more general extremal result simultaneously for a class of indices. In the following, we consider two kinds of index functions, that is, a vertex-weight index function and an edge-weight index function.

Definition 4.1

The weight $\omega (u)$ of a vertex u in a graph G is $e_{G}(u)$. Given a positive real-valued function $t_{v}$, the vertex-weight index function for a graph G is defined by $f(G;v)=\sum_{u\in V(G)} t_{v}(\omega (u))$.

The total eccentricity index of G, introduced by Farooq et al. [8], is defined as $\tau (G)=\sum_{u\in V(G)} e_{G}(u)$ using $t_{v}(\omega (u))=\omega (u)$; the average eccentricity of G, introduced by Bukley et al. [1], is defined as $avec(G)=\frac{1}{n}\tau (G)$ using $t_{v}(\omega (u))=\frac{1}{n}\omega (u)$. For more recent results on average eccentricity, see [2, 3, 5, 11].

The first Zagreb eccentricity index of G is defined as $\xi _{1}(G)=\sum_{u\in V(G)}e^{2}_{G}(u)$ using $t_{v}(\omega (u))=\omega ^{2}(u)$.

Note that those above indices have similar extremal values (or perhaps several near-extremal values) over n-vertex trees, unicyclic graphs, and bicyclic graphs. Tang and Zhou have determined similar extremal values of the average eccentricity over n-vertex trees [18] and unicyclic graphs [19]. Like the discussion of the first Zagreb eccentricity index, we also obtain a similar result about the average eccentricity of bicyclic graphs in the following Theorem 4.2, whose proof is omitted since we use a similar method.

Theorem 4.2

Among the graphs in $\mathbf{B}_{n_{\ge 6}}$, $B_{n}(i)$ is the unique graph with the $(i+1)$th largest average eccentricity, equal to $\frac{3(n-1)^{2}+2n-4i-11}{4n}$ for even n and $\frac{3(n-1)^{2}+2n-4i-10}{4n}$ for odd n, where $0\le i\le \lfloor \frac{n}{2}\rfloor -3$.

Definition 4.3

The weight $\omega (e)$ of an edge $e=uv$ in a graph G is $e_{G}(u)e_{G}(v)$, and the weight $\omega ^{*}(e)$ of an edge $e=uv$ in a graph G is $e_{G}(u)+e_{G}(v)$. Given a positive real-valued function $t_{e}$, the edge-weight index functions for a graph G are defined by $f_{1}(G;e)=\sum_{e\in E(G)} t_{e}(\omega (e))$, $f_{2}(G;e)=\sum_{e\in E(G)} t_{e}(\omega ^{*}(e))$, and $f_{3}(G;e)=\sum_{e\in E(G)} t_{e}(\omega (e),\omega ^{*}(e))$, respectively.

The second Zagreb eccentricity index of G is defined as $\xi _{2}(G)=\sum_{uv\in E(G)}e_{G}(u)e_{G}(v)$ using $t_{e}(\omega (e))=\omega (e)$. The eccentric connectivity index of G, introduced by Sharma et al. in [17], is defined as $\xi ^{c}(G)=\sum_{v\in V(G)}e_{G}(v)d_{G}(v)=\sum_{uv \in E(G)} (e_{G}(u)+e_{G}(v) )$ using $t_{e}(\omega ^{*}(e))=\omega ^{*}(e)$, which is also called the third Zagreb eccentricity index by Ghorbani et al. [10]. For some recent results of the eccentric connectivity index, see [14, 23].

Like the discussion of the second Zagreb eccentricity index, we also obtain similar results about the eccentric connectivity index of trees, unicyclic graphs, and bicyclic graphs in the following propositions and theorems (omitting their proofs).

Theorem 4.4

Among the graphs in $\mathbf{T}_{n_{\ge 3}}$, $P_{n}$ for $n \geq 3$ is the unique graph with the largest eccentricity connectivity index $\xi ^{c}$, equal to $\frac{1}{2}(3n^{2}-6n+4)$ for even n and $\frac{1}{2}(3n^{2}-6n+3)$ for odd n, and $T_{n}^{i}$ is the unique graph with the $(i+1)$th largest eccentricity connectivity index $\xi ^{c}$, equal to $\frac{1}{2}(3n^{2}-8n-4i+6)$ for even n and $\frac{1}{2}(3n^{2}-8n-4i+7)$ for odd n, where $1\leq i \leq \lfloor n/2-1\rfloor$.

Proposition 4.5

Among the graphs in $\mathbf{U}(n_{\ge 6},d_{=n-2})$, $P_{n,3}(i)$ with $0\le i \le \lfloor \frac{n-4}{2}\rfloor$ is the unique graph with the $(2i+1)$th largest eccentricity connectivity index $\xi ^{c}$, and $P_{n,4}(i-1)$ with $1\le i \le \lfloor \frac{n-4}{2}\rfloor$ is the unique graph with the $(2i)$th largest eccentricity index $\xi ^{c}$.

Theorem 4.6

Among the graphs in $\mathbf{U}_{n_{\ge 6}}$, $P_{n,3}(i)$ with $0\le i \le \lfloor (n+3)/4\rfloor$ is the unique graph with the $(2i+1)$th largest eccentricity connectivity index $\xi ^{c}$, equal to $\frac{1}{2}(3n^{2}-4n-8i-6)$ for even n and $\frac{1}{2}(3n^{2}-4n-8i-5)$ for odd n, and $P_{n,4}(i-1)$ with $1\le i \le \lfloor (n+3)/4\rfloor$ is the unique graph with the $(2i)$th largest eccentricity connectivity index $\xi ^{c}$, equal to $\frac{1}{2}(3n^{2}-4n-8i-4)$ for even n and $\frac{1}{2}(3n^{2}-4n-8i-3)$ for odd n.

Proposition 4.7

Among the graphs in $\mathbf{B}(n_{\ge 6},d_{=n-2})$, $B_{n}(i)$ with $0\le i \le \lfloor \frac{n-6}{2}\rfloor$ is the unique graph with the $(i+1)$th largest eccentricity connectivity index $\xi ^{c}$.

Theorem 4.8

Among all the graphs in $\mathbf{B}_{n_{\ge 6}}$, $B_{n}(i)$ is the $(i+1)$ th largest eccentricity connectivity index $\xi ^{c}$, equal to $\frac{1}{2}(3n^{2}-12i-24)$ for even n and $\frac{1}{2}(3n^{2}-12i-23)$ for odd n, where $0\le i \le \lfloor \frac{n}{6} \rfloor$.

In addition, the eccentricity based geometric-arithmetic (GA) index of G, introduced by Ghorbani and Khaki [9], is defined as $GA_{4}(G)=\sum_{uv\in E(G)} \frac{2\sqrt{e_{G}(u)e_{G}(v)}}{e_{G}(u)+e_{G}(v)}$ using $t_{e}(\omega (e),\omega ^{*}(e))= \frac{2\sqrt{\omega (e)}}{\omega ^{*}(e)}$. The ABC eccentric index of G (a new version of the ABC index), introduced by Farahani [7], is defined as $ABC_{5}(G)=\sum_{uv\in E(G)}\sqrt{ \frac{e_{G}(u)+e_{G}(v)-2}{e_{G}(u)e_{G}(v)}}$ using $t_{e}(\omega (e),\omega ^{*}(e))=\sqrt{ \frac{\omega ^{*}(e)-2}{\omega (e)}}$. We speculate that the extremal problems for $GA_{4}(G)$ and $ABC_{5}(G)$ can be solved by using some similar methods.