An improved approach for studying oscillation of generalized Emden–Fowler neutral differential equation

Abstract

The purpose of this work is to study the oscillation criteria for generalized Emden–Fowler neutral differential equation. We establish new oscillation criteria using both the technique of comparison with first order delay equations and the technique of Riccati transformation. Our new criteria are interesting as they improve, simplify, and complement some results that have been published recently in the literature. Moreover, we present an illustrating example.

1 Introduction

In aeromechanical systems, where they have a significant role, in the theory of automatic control, in study of vibrating masses attached to an elastic bar (as the Euler equation), in the networks that have lossless transmission lines (as is the case in high-speed computers), and other applications, delay or neutral differential equations can be seen in the modeling of the mentioned phenomena, see [1, 2, 5, 15]. As a result of these applications, research groups including us still study the differential equations with delay. The theory of oscillation of delay differential equations comes at the forefront of topics that have received the attention of researchers in recent times, see [1–29]. In the last decade, there has been a research movement to improve and develop the oscillation criteria of solutions of second order differential equations with delay (see [9, 10]), neutral (see [3, 7, 13]) and advanced (see [4, 13]).

In this work, we present new oscillation criteria for second-order Emden–Fowler delay differential equations of neutral type

$$ \bigl( r \bigl( \upsilon^{\prime} \bigr) ^{\alpha} \bigr) ^{ \prime} ( t ) +q ( t ) f \bigl( u \bigl( \sigma( t ) \bigr) \bigr) =0, \quad t\geq t_{0}, $$

(1.1)

where $\upsilon ( t ) =u ( t ) +p ( t ) u ( \tau ( t ) )$ and α is a ratio of odd positive integers. We also assume that $r\in C^{1} ( [t_{0},\infty), ( 0,\infty ) )$, $\tau,\sigma,p,q\in C^{1} ( [t_{0},\infty),\mathbb{R} )$, $\sigma ( t ) \leq t$, $\tau ( t ) \leq t$, $0\leq p ( t ) <\min \{ \pi ( t ) /\pi ( \tau ( t ) ) ,1 \}$, $q ( t ) \geq0$, $\lim_{t\rightarrow\infty}\tau ( t ) =\lim_{t \rightarrow\infty}\sigma ( t ) =\infty$, and

$$ \pi( t_{0} ) := \int_{t_{0}}^{\infty} \frac{1}{r^{\frac{1}{\alpha}} ( \nu ) }\, \mathrm{d}\nu < \infty. $$

For the function f, we suppose that $f\in C ( \mathbb{R} ,\mathbb{R} )$ and satisfies the following condition:

$$ f ( u ) >ku^{\beta}\quad\text{for all }u\neq0, $$

where k is a positive constant and β is a quotient of odd positive integers.

A solution of (1.1) means $u\in C ( [t_{0},\infty),[0,\infty) )$ with $t_{a}=\min\{\tau ( t_{b} ) ,\sigma ( t_{b} ) \}$, for some $t_{b}>t_{0}$, which satisfies the property $r ( \upsilon^{\prime} ) ^{\alpha}\in C^{1} ( [t_{a}, \infty),[0,\infty) )$ and satisfies (1.1) on $[t_{b},\infty)$. We consider the nontrivial solutions of (1.1) existing on some half-line $[t_{b},\infty)$ and satisfying the condition

$$ \bigl\{ \bigl\vert u ( t ) \bigr\vert :t_{c}\leq t< \infty\bigr\} >0 \quad \text{for any }t_{c}\geq t_{b}. $$

If u is neither positive nor negative eventually, then $u ( t )$ is called oscillatory, or it will be nonoscillatory.

For canonical form (if $\eta ( t_{0} ) =\infty$), there have been some studies that consider the oscillation and nonoscillation criteria of solutions of (1.1), see for example [19, 24].

For noncanonical form (if $\eta ( t_{0} ) <\infty$), Liu et al. [18] got necessary and appropriate conditions that ensure all solutions of (1.1) can be oscillatory, or they can tend to zero, following the conditions $\lim_{t\rightarrow\infty}p ( t ) =C$,

$$ p^{\prime} ( t ) \geq0\quad \text{and} \quad \tau^{\prime} ( t ) \geq 0. $$

(1.2)

Furthermore, Saker [23] developed the results of [18] in the sense that they established the conditions that assure all the solutions of Eq. (1.1) are oscillatory. The results of both [23] as well as [18] follow an approach that does lead to two conditions, and they are requested (1.2).

Wu et al. [28] established some criteria of oscillation for the neutral equation

$$ \bigl( r ( t ) \bigl\vert \upsilon^{\prime} ( t ) \bigr\vert ^{\alpha-1}\upsilon^{\prime} ( t ) \bigr) ^{\prime}+q ( t ) \bigl\vert u \bigl( \sigma( t ) \bigr) \bigr\vert ^{\beta-1}u \bigl( \sigma( t ) \bigr) =0, $$

(1.3)

under conditions (1.2),

$$ r^{\prime} ( t ) \geq0,\quad \text{and}\quad \sigma( t ) \leq\tau( t ) . $$

(1.4)

This work aims at developing the oscillation theory of second order quasi-linear equations with delay argument. The use of the technique of comparison with first order delay equations and the technique of Riccati transformation helps us to get two various conditions, ensuring oscillation of (1.1) without requiring (1.2). In this paper, in the first two theorems, we simplify results in [18, 23, 28] and obtain new criteria for ensuring oscillation of (1.1) without checking the additional conditions. Our criteria complement and extend the results in [7, 8]. In [7, Theorem 2.2], Bohner et al. proved that equation (1.1) with $\alpha=\beta$ is oscillatory if

$$ W:=\mathop{\lim\sup}_{t\rightarrow\infty} \pi^{\alpha}(t) \int_{t_{0}}^{t}q ( \nu) \biggl( 1-p(\nu) \frac{\pi ( \tau ( \sigma ( \nu ) ) ) }{\pi ( \sigma ( \nu ) ) } \biggr) ^{\alpha}\,\mathrm{d}\nu>1. $$

In our paper, Theorems 2.5 and 2.6 substantially improve Theorem 2.2 in [7, Theorem 2.2], when $W\leq1$.

The next lemma collects two useful inequalities that can be found in [29].

Lemma 1.1

Letαbe a ratio of two odd positive integers. Then

$$ DV-CV^{{ ( \alpha+1 ) /\alpha}}\leq\frac{\alpha^{\alpha}}{(\alpha +1)^{\alpha+1}}\frac{D^{\alpha+1}}{C^{\alpha}},\quad C>0, $$

(1.5)

and

$$ A^{ ( \alpha+1 ) /\alpha}- ( A-B ) ^{ ( \alpha+1 ) /\alpha}\leq\frac{1}{\alpha}B^{1/\alpha} \bigl[ ( 1+\alpha) A-B \bigr] ,\quad \alpha\geq1, AB \geq0. $$

(1.6)

2 Main results

In this section, we shall establish new oscillation criteria for (1.1). Let us define

$$\begin{aligned}& Q ( t ) :=q ( t ) \biggl( 1-p(t) \frac{\pi ( \tau ( \sigma ( t ) ) ) }{\pi ( \sigma ( t ) ) } \biggr) ^{\beta}, \\& \widehat{Q} ( t ) := \biggl( \frac{k}{r ( t ) } \int_{t_{1}}^{t}Q ( \nu) \,\mathrm{d}\nu\biggr) ^{1/ \alpha}, \end{aligned}$$

and

$$ \eta( t ) := \textstyle\begin{cases} 1 & \mbox{if }\alpha=\beta, \\ a_{1} & \mbox{if }\alpha>\beta, \\ a_{2}\pi^{\beta-\alpha} ( t ) & \mbox{if } \alpha< \beta, \end{cases} $$

where $t_{1}\in [ t_{0},\infty )$ and $a_{1}$, $a_{2}$ are any positive constants.

Lemma 2.1

Assume thatuis an eventually nonincreasing positive solution of (1.1). Then$\upsilon^{\beta-\alpha} ( t ) \geq\eta ( t )$.

Proof

Let υ be an eventually positive solution of (1.1) and $\upsilon^{\prime}(t)<0$. Then we have the following cases:

In the case where $\alpha=\beta$, it is easy to see that $\upsilon^{\beta-\alpha} ( t ) =1$.

Let $\alpha>\beta$. Since $\upsilon ( t )$ is a nonincreasing positive function, there exists $M_{1}>0$ such that $\upsilon ( t ) \leq M_{1}$, which implies that

$$ \upsilon^{\beta-\alpha} ( t ) \geq M_{1}^{\beta- \alpha}=a_{1}. $$

In the case $\alpha<\beta$, by using the decreasing property of $r ( \upsilon^{\prime} ) ^{\alpha}$, we obtain

$$ r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha}\leq r ( t_{1} ) \bigl( \upsilon^{ \prime} ( t_{1} ) \bigr) ^{\alpha}=-M_{2}< 0, $$

hence

$$ \upsilon^{\prime} ( t ) \leq\biggl( \frac{-M_{2}}{r ( t ) } \biggr) ^{\frac{1}{\alpha}}. $$

Integrating the last inequality from t to ∞, we get

$$ -\upsilon( t ) \leq-M_{2}^{\frac{1}{\alpha}}\pi( t ) . $$

Thus, we include that

$$ \upsilon^{\beta-\alpha} ( t ) \geq M_{2}^{ \frac{\beta-\alpha}{\alpha}}\pi ^{\beta-\alpha} ( t ) =a_{2}\pi^{\beta- \alpha} ( t ) . $$

Therefore, we have $\upsilon^{\beta-\alpha} ( t ) \geq\eta ( t )$. The proof of the lemma is complete. □

Lemma 2.2

Letube a positive solution of (1.1) on$[ t_{0},\infty )$. If

$$ \int_{t_{1}}^{\infty}Q ( \nu) \,\mathrm{d}\nu=\infty $$

(2.1)

for$t_{1}\geq t_{0}$, then

(H):

υis decreasing, $r ( \upsilon ^{\prime} ) ^{\alpha}$is nonincreasing, eventually.

Proof

Let u be a positive solution of (1.1) on $[ t_{0},\infty )$. Then we suppose that there exists $t_{1}\in [ t_{0},\infty )$ such that $u ( t ) >0$, $u ( \tau ( t ) ) >0$, and $u ( \sigma ( t ) ) >0$ for all $t\in [ t_{1},\infty )$. Obviously, we find $\upsilon ( t ) \geq u ( t )$ and

$$ \bigl( r \bigl( \upsilon^{\prime} \bigr) ^{\alpha} \bigr) ^{ \prime} ( t ) =-q ( t ) f \bigl( u \bigl( \sigma( t ) \bigr) \bigr) \leq0. $$

(2.2)

Therefore, $\upsilon^{\prime}$ is either eventually negative or eventually positive.

Suppose now that $\upsilon^{\prime}>0$ on $[ t_{1},\infty )$. Then $u ( t ) \geq ( 1-p ( t ) ) \upsilon ( t )$, and (2.2) becomes

$$ \bigl( r \bigl( \upsilon^{\prime} \bigr) ^{\alpha} \bigr) ^{ \prime} ( t ) \leq-kq ( t ) \bigl( 1-p \bigl( \sigma( t ) \bigr) \bigr) ^{\beta}\upsilon^{\beta} \bigl( \sigma( t ) \bigr) . $$

(2.3)

Since $\pi ( \tau ( \sigma ( t ) ) ) \geq\pi ( \sigma ( t ) )$, we get

$$ 1-p \bigl( \sigma( t ) \bigr) \geq1-p \bigl( \sigma( t ) \bigr) \frac{\pi ( \tau ( \sigma ( t ) ) ) }{\pi ( \sigma ( t ) ) }. $$

(2.4)

Integrating (2.3) from $t_{1}$ to t and using (2.4), we get

$$\begin{aligned} r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha} \leq&r ( t_{1} ) \bigl( \upsilon^{ \prime} ( t_{1} ) \bigr) ^{\alpha}-k \int_{t_{1}}^{t}q ( \nu) \bigl( 1-p \bigl( \sigma ( \nu) \bigr) \bigr) ^{\beta}\upsilon^{\beta} \bigl( \sigma( t ) \bigr) \,\mathrm{d}\nu \\ \leq&r ( t_{1} ) \bigl( \upsilon^{\prime} ( t_{1} ) \bigr) ^{\alpha}-k\upsilon^{\beta} \bigl( \sigma( t_{1} ) \bigr) \int_{t_{1}}^{t}q ( \nu) \bigl( 1-p \bigl( \sigma ( \nu) \bigr) \bigr) ^{\beta} \,\mathrm{d}\nu \\ \leq&r ( t_{1} ) \bigl( \upsilon^{\prime} ( t_{1} ) \bigr) ^{\alpha}-k\upsilon^{\beta} \bigl( \sigma( t_{1} ) \bigr) \int_{t_{1}}^{t}Q ( \nu) \,\mathrm{d}\nu, \end{aligned}$$

a contradiction with positivity of $\upsilon^{\prime} ( t )$. The proof of this lemma is complete. □

Lemma 2.3

Letube a positive solution of (1.1) on$[ t_{0},\infty )$. If

$$ \int_{t_{1}}^{\infty} \biggl( \frac{1}{r ( s ) } \int_{t_{2}}^{s}Q ( v ) \,\mathrm{d}v \biggr) ^{1/\alpha}\,\mathrm{d}s=\infty $$

(2.5)

for$t_{1}\geq t_{0}$, then$(\mathbf{H})$holds and

$$ \lim_{t\rightarrow\infty}\upsilon( t ) =\infty. $$

(2.6)

Proof

Let u be a positive solution of (1.1) on $[ t_{0},\infty )$. From $\pi ( t_{0} ) <\infty$ and (2.5), we have that (2.1) holds. Hence, from Lemma 2.2, we have that $\upsilon^{\prime} ( t ) <0$, (2.3) and (2.4) hold.

Now, since $\upsilon>0$ and $\upsilon^{\prime}<0$, we get that $\lim_{t\rightarrow\infty}\upsilon ( t ) =c\geq0$. Suppose that $c>0$. Then there exists $t_{2}\geq t_{1}$ such that $\upsilon ( \sigma ( t ) ) \leq c$. From (2.3) and (2.4), we obtain

$$ \bigl( r \bigl( \upsilon^{\prime} \bigr) ^{\alpha} \bigr) ^{ \prime} ( t ) \leq-kc^{\beta}Q ( t ) $$

for $t\geq t_{2}$. Integrating two times this inequality from $t_{2}$ to t, we get, after the first integration,

$$ \upsilon^{\prime} ( t ) \leq- \bigl( kc^{\beta} \bigr) ^{1/\alpha} \biggl( \frac{1}{r ( t ) } \int_{t_{2}}^{t}Q ( s ) \,\mathrm{d}s \biggr) ^{1/\alpha}. $$

After the second integration, we obtain

$$ \upsilon( t ) -\upsilon( t_{2} ) \leq- \bigl( kc^{\beta} \bigr) ^{1/\alpha} \int_{t_{2}}^{t} \biggl( \frac{1}{r ( s ) } \int_{t_{2}}^{s}Q ( v ) \,\mathrm{d}v \biggr) ^{1/ \alpha}\,\mathrm{d}s. $$

This implies that $\lim_{t\rightarrow\infty}\upsilon(t)=-\infty$, which contradicts $\upsilon>0$. The proof of this lemma is complete. □

Theorem 2.1

If

$$ \int_{t_{1}}^{\infty} \biggl( \frac{1}{r ( t ) } \int_{t_{1}}^{t}Q ( \nu) \pi^{\beta} \bigl( \sigma( \nu) \bigr) \,\mathrm{d}\nu\biggr) ^{1/\alpha}\, \mathrm{d}t= \infty $$

(2.7)

for$t_{1}\geq t_{0}$, then (1.1) is oscillatory.

Proof

Let u be a positive solution of (1.1) on $[ t_{0},\infty )$ (assume the converse). Then we suppose that there exists $t_{1}\in [ t_{0},\infty )$ such that $u ( t ) >0$, $u ( \tau ( t ) ) >0$ and $u ( \sigma ( t ) ) >0$ for all $t\in [ t_{1},\infty )$. Since $\pi ( t_{0} ) <\infty$ and (2.7), we have that $\int_{t_{1}}^{t}Q ( \nu ) \pi^{\beta} ( \sigma ( \nu ) ) \,\mathrm{d}\nu$ must be unbounded. Thus, and from the fact $\pi^{\prime} ( t ) <0$, it is easy to see that (2.1) holds. Hence, from Lemma 2.2, we have that $\upsilon^{\prime} ( t ) <0$ and (2.2) holds. Since

$$ \upsilon(t)\geq- \int_{t}^{\infty}\upsilon^{\prime}(\nu) \,\mathrm{d}\nu=- \int_{t}^{\infty} \frac{r^{1/\alpha}(\nu)\upsilon^{\prime} ( \nu ) }{r^{1/\alpha} ( \nu ) } \,\mathrm{d} \nu\geq-\pi(t)r^{1/\alpha}(t)\upsilon^{\prime}(t), $$

(2.8)

it follows that

$$ \frac{\mathrm{d}}{\mathrm{d}t} \biggl( \frac{\upsilon ( t ) }{\pi ( t ) } \biggr) \geq0. $$

In view of the definition of υ, we deduce

$$\begin{aligned} u ( t ) =&\upsilon( t ) -p ( t ) \bigl( u \bigl( \tau( t ) \bigr) \bigr) \geq \upsilon( t ) -p ( t ) \bigl( \upsilon\bigl( \tau( t ) \bigr) \bigr) \\ \geq&\upsilon( t ) \biggl( 1-p(t) \frac{\pi ( \tau ( t ) ) }{\pi ( t ) } \biggr) . \end{aligned}$$

Consequently, (2.2) becomes

$$\begin{aligned} \bigl( r \bigl( \upsilon^{\prime} \bigr) ^{\alpha} \bigr) ^{ \prime} ( t ) \leq&-kq ( t ) \biggl( 1-p(t) \frac{\pi ( \tau ( \sigma ( t ) ) ) }{\pi ( \sigma ( t ) ) } \biggr) ^{\beta}\upsilon^{\beta} \bigl( \sigma( t ) \bigr) \\ =&-kQ(t)\upsilon^{\beta}\bigl(\sigma(t)\bigr). \end{aligned}$$

(2.9)

From the monotonicity property of $r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha}$, we have

$$ -r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha}\geq-r ( t_{1} ) \bigl( \upsilon^{ \prime} ( t_{1} ) \bigr) ^{\alpha}=:L>0, $$

which in view of (2.8) implies

$$ \upsilon^{\beta} ( t ) \geq L^{\frac{\beta}{\alpha}} \pi^{\beta} ( t ) . $$

(2.10)

From (2.10), (2.9) becomes

$$ \bigl( r \bigl( \upsilon^{\prime} \bigr) ^{\alpha} \bigr) ^{ \prime} ( t ) \leq-kL^{\frac{\beta}{\alpha}}Q ( t ) \pi^{\beta} \bigl( \sigma( t ) \bigr) . $$

(2.11)

Integrating (2.11) from $t_{1}$ to t, we obtain

$$\begin{aligned} r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha} \leq&r ( t_{1} ) \bigl( \upsilon^{ \prime} ( t_{1} ) \bigr) ^{\alpha}-kL^{ \frac{\beta}{\alpha}} \int_{t_{1}}^{t}Q ( \nu) \pi^{ \beta} \bigl( \sigma(\nu) \bigr) \,\mathrm{d}\nu \\ \leq&-kL^{\frac{\beta}{\alpha}} \int_{t_{1}}^{t}Q ( \nu) \pi^{\beta} \bigl( \sigma( \nu) \bigr) \,\mathrm{d}\nu. \end{aligned}$$

(2.12)

Integrating (2.12) from $t_{1}$ to t and using (2.7), we get

$$ \upsilon( t ) \leq\upsilon( t_{1} ) -k^{ \frac{1}{\alpha}}L^{\beta} \int_{t_{1}}^{t} \biggl( \frac{1}{r ( \nu ) } \int_{t_{1}}^{\nu}Q ( v ) \pi^{\beta} \bigl( \sigma( v ) \bigr) \,\mathrm{d}v \biggr) ^{\frac{1}{\alpha}} \, \mathrm{d}\nu, $$

which in view of (2.7) contradicts the positivity of $\upsilon ( t )$. The proof of the theorem is complete. □

Theorem 2.2

Assume that$\sigma^{\prime} ( t ) >0$. If

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \pi^{\alpha}(t)\eta( t ) \int_{t_{1}}^{t}Q(\nu)\,\mathrm{d}\nu>1 $$

(2.13)

for$t_{1}\geq t_{0}$, then (1.1) is oscillatory.

Proof

To the contrary, we suppose that u is a positive solution of (1.1) on $[ t_{0},\infty )$. Then there exists $t_{1}\geq t_{0}$ such that $u ( \tau ( t ) ) >0$ and $u ( \sigma ( t ) ) >0$ for all $t\geq t_{1}$. From (2.13) and $\pi ( t_{0} ) <\infty$, we get (2.1) holds. Using Lemma 2.2, we get that $\upsilon^{\prime}<0$ on $[ t_{1},\infty )$. As in the proof of Theorem 2.1, we get (2.8) and (2.9) hold. By integrating (2.9) from $t_{1}$ to t, we get

$$\begin{aligned} r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha} \leq&r ( t_{1} ) \bigl( \upsilon^{ \prime} ( t_{1} ) \bigr) ^{\alpha}-k \int_{t_{1}}^{t}Q( \nu)\upsilon^{\beta} \bigl( \sigma( \nu) \bigr) \,\mathrm{d}\nu \\ \leq&-k\upsilon^{\beta} \bigl( \sigma( t ) \bigr) \int_{t_{1}}^{t}Q(\nu)\,\mathrm{d}\nu. \end{aligned}$$

(2.14)

Since $\sigma ( t ) \leq t$ and $\upsilon^{\prime} ( t ) <0$, we obtain

$$ r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha}\leq-k \upsilon^{\alpha}(t)\upsilon^{\beta- \alpha}(t) \int_{t_{1}}^{t}Q(\nu)\,\mathrm{d}\nu. $$

By Lemma 2.1 and (2.8) we arrive at

$$ -r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha}\geq-r ( t ) \bigl( \upsilon^{ \prime} ( t ) \bigr) ^{\alpha}\pi ^{\alpha} ( t ) \eta( t ) \int_{t_{1}}^{t}Q(\nu)\,\mathrm{d} \nu, $$

and so

$$ \pi^{\alpha} ( t ) \eta( t ) \int_{t_{1}}^{t}Q( \nu)\,\mathrm{d}\nu\leq1, $$

(2.15)

a contradiction with (2.13). Then the proof is complete. □

Theorem 2.3

Assume that (2.1) holds. If the first order delay differential equation

$$ \upsilon^{\prime} ( t ) +\widehat{Q} ( t ) \upsilon^{\beta/\alpha} \bigl( \sigma( t ) \bigr) =0 $$

(2.16)

is oscillatory, then (1.1) is oscillatory.

Proof

To the contrary, we suppose that u is a positive solution of (1.1) on $[ t_{0},\infty )$. Then there exists $t_{1}\geq t_{0}$ such that $u ( \tau ( t ) ) >0$ and $u ( \sigma ( t ) ) >0$ for all $t\geq t_{1}$. Using (2.1) and Lemma 2.2, we get that $\upsilon^{\prime}<0$ on $[ t_{1},\infty )$. As in the proof of Theorem 2.2, we get (2.14) holds. From (2.14), it is clear that υ is a positive solution of the first order differential inequality

$$ \upsilon^{\prime} ( t ) +\widehat{Q} ( t ) \upsilon^{\beta/\alpha} \bigl( \sigma( t ) \bigr) \leq0. $$

In view of [25, Lemma 1], we see that the first-order delay differential equation (2.16) has a positive solution, a contradiction. Then the proof is complete. □

Corollary 2.1

Assume that$\alpha=\beta$. If

$$ \mathop{\lim\inf}_{t\rightarrow\infty} \int_{\sigma ( t ) }^{t}\widehat{Q} ( \nu) \,\mathrm{d}\nu >\frac{1}{\mathrm{e}}, $$

(2.17)

then (1.1) is oscillatory.

Proof

In view of [16, Theorem 2], condition (2.17) implies oscillation of (2.16). On the other hand, if suffices to note that

$$ \int_{t_{0}}^{\infty}\widehat{Q} ( \nu) \,\mathrm{d}\nu= \infty $$

is necessary for the validity of (2.1). Therefore, the proof is complete. □

Corollary 2.2

Assume that$\alpha>\beta>0$. If

$$ \int_{t_{0}}^{\infty}\widehat{Q} ( \nu) \,\mathrm{d}\nu= \infty, $$

(2.18)

then (1.1) is oscillatory.

Proof

Since $\beta/\alpha\in ( 0,1 )$, it is shown that all the solutions of (2.16) oscillate if and only if (2.18) holds, see [12] and [17]. On the other hand, we see that (2.18) is necessary for the validity of (2.1). Therefore, the proof is complete. □

Corollary 2.3

Assume that$\alpha<\beta$, $\sigma ( t )$is continuously differentiable, $\sigma^{\prime} ( t ) >0$and (2.1) holds. If there exists a continuously differentiable function$\xi ( t )$such that$\xi^{\prime} ( t ) >0$, $\lim_{t\rightarrow\infty}\xi ( t ) =\infty$,

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \frac{\beta\xi^{\prime} ( \sigma ( t ) ) \sigma^{\prime} ( t ) }{\alpha\xi^{\prime} ( t ) }< 1, $$

and

$$ \mathop{\lim\inf}_{t\rightarrow\infty} \biggl[ \frac{\widehat{Q} ( t ) }{\xi^{\prime} ( t ) }e^{-\xi ( t ) } \biggr] >0, $$

(2.19)

then (1.1) is oscillatory.

Proof

In view of [25, Theorem 1], condition (2.19) implies oscillation of (2.16). □

The following results serve as an improvement of Theorems 2.2, when $\alpha=\beta$ and

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \pi^{\alpha}(t)\eta( t ) \int_{t_{1}}^{t}Q(\nu)\,\mathrm{d}\nu\leq1. $$

For the simplicity, we define the following notations:

$$ m:=\mathop{\lim\inf}_{t\rightarrow\infty} \frac{k}{\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s $$

and

$$ M:=\mathop{\limsup}_{t\rightarrow\infty}\pi( t ) \biggl( k \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s \biggr) ^{1/\alpha}. $$

Theorem 2.4

Assume that$\alpha=\beta$and (2.5) is satisfied. If

$$ m>\alpha $$

(2.20)

or

$$ m\leq\alpha\quad \textit{and}\quad M>1-\frac{m}{\alpha}, $$

(2.21)

then (1.1) is oscillatory.

Proof

Suppose against the assumption of theorem that equation (1.1) has a nonoscillatory solution u on $[ t_{0},\infty )$. Without loss of generality, we may assume that $u ( t ) >0$ and $u ( \sigma ( t ) ) >0$ for $t\geq t_{1}\geq t_{0}$. Let

$$ g^{\prime} ( t ) = \bigl( \upsilon( t ) +r^{1/ \alpha} ( t ) \upsilon^{\prime} ( t ) \pi( t ) \bigr) ^{\prime}=\pi( t ) \bigl( r^{1/ \alpha} ( t ) \upsilon^{\prime} ( t ) \bigr) ^{\prime}, $$

(2.22)

then

$$ \bigl( \bigl( r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \bigr) ^{\alpha} \bigr) ^{\prime}=\alpha\bigl( r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \bigr) ^{\alpha-1} \bigl( r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \bigr) ^{\prime}. $$

(2.23)

Combining (2.22) and (2.23), and using inequality (2.9), we get

$$\begin{aligned} g^{\prime} ( t ) =&\frac{1}{\alpha}\pi( t ) \bigl( r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \bigr) ^{1-\alpha} \bigl( \bigl( r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha} \bigr) \bigr) ^{\prime} \\ \leq&-\frac{k}{\alpha}\pi( t ) \bigl( r^{1/\alpha} ( t ) \upsilon ^{\prime} ( t ) \bigr) ^{1- \alpha}Q ( t ) \upsilon^{\alpha} \bigl( \sigma( t ) \bigr) . \end{aligned}$$

(2.24)

Integrating (2.24) from t to ∞, we get

$$\begin{aligned} g ( t ) \geq&\frac{k}{\alpha} \int_{t}^{\infty}\pi( s ) Q ( s ) \bigl( r^{1/\alpha} ( s ) \upsilon^{\prime} ( s ) \bigr) ^{1-\alpha} \upsilon^{\alpha} ( s ) \,\mathrm{d}s \\ \geq&-\frac{k}{\alpha} \int_{t}^{\infty}\pi( t ) Q ( s ) \bigl( r^{\frac{1}{\alpha}} ( s ) \upsilon^{\prime} ( s ) \bigr) ^{1-\alpha} \bigl( - \pi( t ) r^{1/\alpha} ( s ) \upsilon^{ \prime} ( s ) \bigr) ^{\alpha-1}\upsilon( s ) \,\mathrm{d}s \\ \geq&\frac{k}{\alpha} \frac{\upsilon ( t ) }{\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s. \end{aligned}$$

It follows that

$$ \upsilon( t ) +r^{1/\alpha} ( t ) \upsilon^{ \prime} ( t ) \pi( t ) \geq\frac{k}{\alpha} \frac{\upsilon ( t ) }{\pi ( t ) } \int_{t}^{ \infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s, $$

and so

$$ \upsilon( t ) \biggl( 1-\frac{k}{\alpha} \frac{1}{\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \geq-r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \pi( t ) >0. $$

(2.25)

Now, let (2.20) hold. It follows from (2.20) that there exists $\epsilon>0$ such that

$$ m-\epsilon>\alpha. $$

By virtue of definition of m, we see that

$$ 1-\frac{k}{\alpha}\frac{1}{\pi ( t ) } \int_{t}^{\infty} \pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s\leq1- \frac{1}{\alpha} ( m-\epsilon) < 0, $$

this contradicts the positivity of υ.

Assume next that the case $m\leq\alpha$ holds. Proceeding as in the proof of Theorem 2.2, we get (2.14). Thus, by (2.25), we get

$$\begin{aligned}& -r^{1/\alpha} ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) \biggl( 1- \frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \\& \quad \geq k\upsilon(t) \biggl( 1- \frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \biggl( \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s \biggr) ^{1/\alpha} \\& \quad \geq-kr^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \pi( t ) \biggl( \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s \biggr) ^{1/\alpha}, \end{aligned}$$

that is,

$$ \biggl( 1-\frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty} \pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \geq k\pi( t ) \biggl( \int_{t_{0}}^{t}Q(s) \,\mathrm{d}s \biggr) ^{\frac{1}{\alpha}}. $$

Hence,

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \pi( t ) \biggl( k \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s \biggr) ^{ \frac{1}{\alpha}}\leq1- \mathop{\lim\inf}_{t\rightarrow\infty} \frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s, $$

which implies

$$ M\leq\frac{\alpha-m}{\alpha}, $$

this contradicts (2.21). Then the proof is complete. □

Lemma 2.4

Assume that (1.1) has an eventually positive solutionuon$[ t_{0},\infty )$. Then there exist$T\geq t_{1}$and$\epsilon>0$such that

$$ \biggl( \frac{\upsilon}{\pi^{N}} \biggr)\quad \textit{is nonincreasing on }[T,\infty), $$

(2.26)

where$N=M-\epsilon$.

Proof

Assume that u is a positive solution of (1.1) on $[T,\infty)$. By Lemma 2.3, $u ( t )$ satisfies $( \mathbf{H} )$ and (2.6). Proceeding as in the proof of Theorem 2.2, we have (2.14) holds. Now, we see that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \biggl( \frac{\upsilon ( t ) }{\pi^{N} ( t ) } \biggr) =& \frac{r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \pi^{N} ( t ) +N\upsilon ( t ) \pi^{N-1} ( t ) }{r^{1/\alpha} ( t ) \pi^{2N} ( t ) } \\ \leq&\frac{\upsilon ( t ) }{r^{1/\alpha} ( t ) \pi^{N+1} ( t ) } \biggl( N+ \frac{r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \pi ( t ) }{\upsilon ( t ) } \biggr) . \end{aligned}$$

(2.27)

In view of (2.14), we note that

$$ \frac{-r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) }{\upsilon ( t ) }\geq\biggl( k \int_{t_{0}}^{t}Q ( s ) \,\mathrm{d}s \biggr) ^{1/\alpha}, $$

which implies

$$ N+ \frac{r^{1/\alpha} ( t ) \upsilon^{\prime} ( t ) \pi ( t ) }{\upsilon ( t ) } \leq N-\pi( t ) \biggl( k \int_{t_{0}}^{t}Q ( s ) \,\mathrm{d}s \biggr) ^{1/\alpha}< 0. $$

Therefore, (2.27) becomes

$$ \frac{\mathrm{d}}{\mathrm{d}t} \biggl( \frac{\upsilon ( t ) }{\pi^{N} ( t ) } \biggr) < 0. $$

Then the proof is complete. □

Theorem 2.5

Assume that$\alpha=\beta$and (2.5) holds. If there is a constantκsuch that

$$ \frac{\pi ( \sigma ( t ) ) }{\pi ( t ) } \geq\kappa>1 $$

(2.28)

for all$t\geq t_{0}$and

$$ M\kappa^{M}>1, $$

(2.29)

then (1.1) is oscillatory.

Proof

Proceeding as in the proof of Theorem 2.2, we get that (2.14) holds. By Lemma 2.4, we see that

$$ \upsilon\bigl( \sigma( t ) \bigr) \geq\upsilon( t ) \kappa ^{N}. $$

(2.30)

From (2.14), we get

$$ -r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha}\geq k \upsilon^{\alpha}(t)\kappa^{\alpha N} \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s. $$

(2.31)

In view of (2.8), we obtain

$$ -r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha}\geq-kr ( t ) \bigl( \upsilon^{ \prime} ( t ) \bigr) ^{\alpha}\pi ^{\alpha} ( t ) \kappa^{\alpha N} \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s. $$

It follows that

$$ 1\geq\kappa^{N}\pi( t ) \biggl( k \int_{t_{0}}^{t}Q(s) \,\mathrm{d}s \biggr) ^{1/\alpha}. $$

Taking the lim sup on both sides, we obtain a contradiction. Then the proof is complete. □

Theorem 2.6

Assume that$\alpha=\beta$, (2.5) holds, and there is a constantκsuch that (2.28) holds. If (2.20) or

$$ m\leq\alpha\quad \textit{and}\quad M\kappa^{M}>1-\frac{m}{\alpha}, $$

then (1.1) is oscillatory.

Proof

As in the proof of Theorem 2.4, if we replace (2.14) by (2.31), then we get

$$\begin{aligned}& -r^{1/\alpha} ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) \biggl( 1- \frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \\& \quad \geq\upsilon(t)\kappa^{N} \biggl( 1- \frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \biggl( k \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s \biggr) ^{1/\alpha}, \end{aligned}$$

and so

$$ \biggl( 1-\frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty} \pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s \biggr) \geq\pi( t ) \kappa^{N} \biggl( k \int_{t_{0}}^{t}Q(s) \,\mathrm{d}s \biggr) ^{\frac{1}{\alpha}}. $$

Taking lim sup on both sides, we obtain

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \pi( t ) \kappa^{N} \biggl( k \int_{t_{0}}^{t}Q(s)\,\mathrm{d}s \biggr) ^{ \frac{1}{\alpha}}\leq1-\mathop{\lim\inf}_{t\rightarrow\infty} \frac{k}{\alpha\pi ( t ) } \int_{t}^{\infty}\pi^{\alpha+1} ( s ) Q ( s ) \,\mathrm{d}s. $$

Therefore,

$$ \kappa^{N}M\leq1-\frac{m}{\alpha}. $$

Then the proof is complete. □

In the next theorems, by using a generalized Riccati substitution, we establish new oscillation criteria of (1.1).

Theorem 2.7

Assume that$\sigma^{\prime} ( t ) >0$and$\alpha\geq1$. If there exist functions$\delta,\varphi\in C^{1} ( [ t_{0},\infty ) , ( 0,\infty ) )$such that

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \int_{t_{0}}^{t} \biggl( \varPsi( \nu) - \frac{\delta ( \nu ) r ( \nu ) ( \varPhi_{+} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}} \biggr) \,\mathrm{d}\nu=\infty $$

(2.32)

and

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \int_{t_{0}}^{t} \biggl( \varphi( \nu) G ( \nu) - \frac{r ( \sigma ( \nu ) ) ( \varphi_{+}^{\prime} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1} ( \varphi ( \nu ) \sigma ^{\prime} ( \nu ) ) ^{\alpha}} \biggr) \,\mathrm{d}\nu=\infty, $$

(2.33)

where

$$\begin{aligned}& \varPhi( t ) := \frac{\delta^{\prime} ( t ) }{\delta ( t ) }+ \frac{1+\alpha}{r^{1/\alpha} ( t ) \pi ( t ) }, \\& \varPsi( t ) :=\delta( t ) \biggl( k\eta( t ) Q ( t ) + \frac{1-\alpha}{r^{1/\alpha} ( t ) \pi^{\alpha+1} ( t ) } \biggr) , \\& G ( t ) :=k\eta\bigl( \sigma( t ) \bigr) q ( t ) \bigl( 1-p\bigl(\sigma( t ) \bigr) \bigr) ^{ \beta} \end{aligned}$$

and$H_{+} ( t ) =\max \{ H ( t ) ,0 \}$, then (1.1) is oscillatory.

Proof

To the contrary, we suppose that u is a positive solution of (1.1) on $[ t_{0},\infty )$. Thus, there exists $t_{1}\geq t_{0}$ such that $u ( \tau ( t ) ) >0$ and $u ( \sigma ( t ) ) >0$ for all $t\geq t_{1}$. Then we get that $\upsilon^{\prime}$ has one sign eventually.

Now, we let $\upsilon^{\prime} ( t ) <0$ for $t\geq t_{1}$. As in the proof of Theorem 2.1, we get (2.9) holds. Define the function $\omega ( t )$ by

$$ \omega( t ) =\delta( t ) \biggl[ \frac{r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha}}{\upsilon^{\alpha} ( t ) }+ \frac{1}{\pi^{\alpha} ( t ) } \biggr] . $$

(2.34)

From (2.8), we see that $\omega ( t ) \geq0$. By differentiating (2.34), we get

$$\begin{aligned} \omega^{\prime} ( t ) =&\frac{\delta^{\prime} ( t ) }{\delta ( t ) }\omega( t ) +\delta( t ) \frac{ ( r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha} ) ^{\prime}}{\upsilon^{\alpha} ( t ) }- \alpha\delta( t ) r ( t ) \biggl( \frac{\upsilon^{\prime} ( t ) }{\upsilon ( t ) } \biggr) ^{\alpha+1} + \frac{\alpha\delta ( t ) }{r^{\frac{1}{\alpha}} ( t ) \pi^{\alpha+1} ( t ) } \\ =&\frac{\delta^{\prime} ( t ) }{\delta ( t ) } \omega( t ) +\delta ( t ) \frac{ ( r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha} ) ^{\prime}}{\upsilon^{\alpha } ( t ) }+ \frac{\alpha\delta ( t ) }{r^{\frac{1}{\alpha}} ( t ) \pi^{\alpha +1} ( t ) } \\ &{}-\alpha\delta( t ) r ( t ) \biggl( \frac{\omega ( t ) }{\delta ( t ) r ( t ) }- \frac{1}{r ( t ) \pi^{\alpha} ( t ) } \biggr) ^{ ( \alpha+1 ) /\alpha}. \end{aligned}$$

(2.35)

Using inequality (1.6) with

$$ A:= \frac{\omega ( t ) }{\delta ( t ) r ( t ) }\quad \text{and}\quad B:= \frac {1}{r ( t ) \pi^{\alpha} ( t ) }, $$

we obtain

$$\begin{aligned} \biggl[ \frac{\omega ( t ) }{\delta ( t ) r ( t ) }- \frac{1}{r ( t ) \pi^{\alpha} ( t ) } \biggr] ^{ \frac{\alpha+1}{\alpha}} \geq& \biggl( \frac{\omega ( t ) }{\delta ( t ) r ( t ) } \biggr) ^{ \frac{\alpha+1}{\alpha}} \\ &{}- \frac{1}{\alpha r ( t ) ^{\frac{1}{\alpha}}\pi ( t ) } \biggl[ \frac{ ( \alpha+1 ) \omega ( t ) }{\delta ( t ) r ( t ) }- \frac{1}{r ( t ) \pi^{\alpha} ( t ) } \biggr] . \end{aligned}$$

(2.36)

Using Lemma 2.1 with (2.9), we have

$$ \frac{ ( r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha} ) ^{\prime}}{\upsilon^{\alpha} ( t ) }\leq-kQ(t) \frac {\upsilon^{\beta}(\sigma(t))}{\upsilon^{\alpha} ( t ) }\leq-k\eta( t ) Q ( t ) . $$

(2.37)

From (2.35)–(2.37), we find

$$\begin{aligned} \omega^{\prime} ( t ) \leq&\frac{\delta^{\prime} ( t ) }{\delta ( t ) }\omega( t ) -k \delta ( t ) \eta( t ) Q ( t ) - \alpha\delta( t ) r ( t ) \biggl( \biggl( \frac{\omega ( t ) }{\delta ( t ) r ( t ) } \biggr) ^{ \frac{\alpha+1}{\alpha}} \\ & {}- \frac{1}{\alpha r ( t ) ^{\frac{1}{\alpha}}\pi ( t ) } \biggl[ ( \alpha+1 ) \frac{\omega ( t ) }{\delta ( t ) r ( t ) }- \frac{1}{r ( t ) \pi^{\alpha} ( t ) } \biggr] \biggr) + \frac{\alpha \delta ( t ) }{r^{\frac{1}{\alpha}} ( t ) \pi^{\alpha+1} ( t ) } \\ =&\varPhi( t ) \omega( t ) -\varPsi( t ) -\alpha\frac{1}{ ( \delta ( t ) r ( t ) ) ^{\frac{1}{\alpha}}}\omega ( t ) ^{\frac{\alpha+1}{\alpha}}. \end{aligned}$$

(2.38)

By inequality 1.5 with $C:=\alpha ( \delta ( t ) r ( t ) ) ^{-1/\alpha}$, $D:=\varPhi ( t )$, and $V:=\omega ( t )$, we obtain

$$ \omega^{\prime} ( t ) \leq-\varPsi( t ) + \frac{\delta ( t ) r ( t ) ( \varPhi ( t ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}}. $$

Integrating from $t_{2}$ to t, we obtain

$$ \int_{t_{2}}^{t} \biggl( \varPsi( \nu) - \frac{\delta ( \nu ) r ( \nu ) ( \varPhi_{+} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}} \biggr) \,\mathrm{d}\nu\leq \omega( t_{2} ) - \omega( t ) \leq\omega( t_{2} ) , $$

which contradicts (2.32).

On the other hand, let $\upsilon^{\prime} ( t ) >0$ for all $t\geq t_{2}$. It is easy to prove that $u ( t ) \geq ( 1-p ( t ) ) \upsilon ( t )$ and

$$ \bigl( r ( t ) \bigl( \upsilon^{\prime} ( t ) \bigr) ^{\alpha} \bigr) ^{\prime}\leq-kq ( t ) \bigl( 1-p \bigl( \sigma( t ) \bigr) \bigr) ^{\beta}\upsilon^{\beta} \bigl( \sigma( t ) \bigr) . $$

(2.39)

Since $( r ( \upsilon^{\prime} ) ^{\alpha} ) ^{ \prime} ( t ) <0$, we find

$$ \upsilon^{\prime} \bigl( \sigma( t ) \bigr) \geq\upsilon ^{\prime} ( t ) \biggl( \frac{r ( t ) }{r ( \sigma ( t ) ) } \biggr) ^{1/\alpha}. $$

(2.40)

Define the function

$$ R ( t ) =\varphi( t ) \frac{r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha}}{\upsilon^{\alpha} ( \sigma ( t ) ) }. $$

Hence, $R ( t ) \geq0$. By differentiating $R ( t )$ and using (2.39) and (2.40), we get

$$ R^{\prime} ( t ) \leq-\varphi( t ) G ( t ) +\frac{\varphi^{\prime} ( t ) }{\varphi ( t ) }R ( t ) - \frac{\alpha\sigma^{\prime} ( t ) }{r^{1/\alpha} ( \sigma ( t ) ) \varphi^{1/\alpha} ( t ) }R^{1+1/\alpha} ( t ) . $$

Proceeding as in the proof of the previous case, we obtain

$$ \int_{t_{0}}^{t} \biggl( \varphi( \nu) G ( \nu) - \frac{r ( \sigma ( \nu ) ) ( \varphi_{+}^{\prime} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1} ( \varphi ( \nu ) \sigma ^{\prime} ( \nu ) ) ^{\alpha}} \biggr) \,\mathrm{d}\nu\leq R ( t_{2} ) , $$

which contradicts (2.33). This completes the proof. □

Theorem 2.8

Assume that$\sigma^{\prime} ( t ) >0$. If there exist functions$\delta,\varphi\in C^{1}( [ t_{0},\infty ) , ( 0,\infty ) )$such that (2.33) holds and

$$ \mathop{\lim\sup}_{t\rightarrow\infty} \biggl( \frac{\pi^{\alpha } ( t ) }{\delta ( t ) } \int_{t}^{t} \biggl( k\delta( \nu) \eta( \nu) Q ( \nu) - \frac{r ( \nu ) ( \delta^{\prime} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}\delta^{\alpha} ( \nu ) } \biggr) \,\mathrm{d}\nu\biggr) >1 $$

(2.41)

for any$t\in [ t_{0},\infty )$, then (1.1) is oscillatory.

Proof

Proceeding as in the proof of Theorem 2.7, we obtain that $\upsilon^{\prime}$ has one sign eventually. For the case where $\upsilon^{\prime} ( t ) <0$ for all $t\geq t_{1}$, let us define the function ω as in (2.34). From (2.35) we have

$$\begin{aligned} \omega^{\prime} ( t ) =&\frac{\delta^{\prime} ( t ) }{\delta ( t ) }\omega( t ) +\delta( t ) \frac{ ( r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha} ) ^{\prime}}{\upsilon^{\alpha} ( t ) }- \frac{\alpha}{ ( \delta ( t ) r ( t ) ) ^{\frac{1}{\alpha}}} \biggl( \omega( t ) - \frac{\delta ( t ) }{\pi^{\alpha} ( t ) } \biggr) ^{\frac{\alpha +1}{\alpha}} \\ &{}+ \frac{\alpha\delta}{r^{\frac{1}{\alpha}} ( t ) \pi^{\alpha+1} ( t ) }. \end{aligned}$$

Using Lemma 1.1 with $C=\delta^{\prime} ( t ) /\delta ( t )$, $D= \alpha ( \delta ( t ) r ( t ) ) ^{ \frac{-1}{\alpha}}$, and $V=\delta ( t ) /\pi^{\alpha} ( t )$, we obtain

$$\begin{aligned} \omega^{\prime} ( t ) \leq&-k\delta( t ) \eta( t ) Q ( t ) + \frac{\delta^{\prime} ( t ) }{\pi^{\alpha} ( t ) }+ \frac{r ( t ) ( \delta^{\prime} ( t ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha +1}\delta^{\alpha} ( t ) }+ \frac{\alpha\delta}{r^{\frac{1}{\alpha }} ( t ) \pi^{\alpha+1} ( t ) } \\ \leq&-k\delta( t ) \eta( t ) Q ( t ) + \biggl( \frac{\delta ( t ) }{\pi^{\alpha} ( t ) } \biggr) ^{\prime}+ \frac{r ( t ) ( \delta^{\prime} ( t ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}\delta^{\alpha} ( t ) }. \end{aligned}$$

(2.42)

Integrating (2.42) from $t_{2}$ to t, we get

$$\begin{aligned}& \int_{t_{2}}^{t} \biggl( k\delta( \nu) \eta( \nu) Q ( \nu) - \frac{r ( \nu ) ( \delta^{\prime} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}\delta^{\alpha} ( \nu ) } \biggr) \,\mathrm{d}\nu- \frac{\delta ( t ) }{\pi^{\alpha} ( t ) }+ \frac{\delta ( t_{2} ) }{\pi^{\alpha} ( t_{2} ) } \\& \quad \leq\omega( t_{2} ) -\omega( t ) . \end{aligned}$$

In view of the definition of $\omega ( t )$, we get

$$\begin{aligned}& \int_{t_{2}}^{t} \biggl( k\delta( \nu) \eta( \nu) Q ( \nu) - \frac{r ( \nu ) ( \delta^{\prime} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}\delta^{\alpha} ( \nu ) } \biggr) \,\mathrm{d}\nu \\& \quad \leq\delta( t_{2} ) \frac{r ( t_{2} ) ( \upsilon^{\prime } ( t_{2} ) ) ^{\alpha}}{\upsilon^{\alpha} ( t_{2} ) }-\delta( t ) \frac{r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha}}{\upsilon ^{\alpha} ( t ) }. \end{aligned}$$

(2.43)

Therefore, from (2.8), it follows that

$$ \frac{r ( t ) ( \upsilon^{\prime} ( t ) ) ^{\alpha}}{\upsilon^{\alpha} ( t ) }\geq- \frac{1}{\pi^{\alpha} ( t ) }. $$

Substituting the above inequality into (2.43), we are led to

$$ \frac{\pi^{\alpha} ( t ) }{\delta ( t ) } \int_{t_{2}}^{t} \biggl( k\delta( \nu) \eta( \nu) Q ( \nu) - \frac{r ( \nu ) ( \delta^{\prime} ( \nu ) ) ^{\alpha+1}}{ ( \alpha+1 ) ^{\alpha+1}\delta^{\alpha} ( \nu ) } \biggr) \,\mathrm{d}\nu\leq1. $$

Now, taking the $\lim\sup_{t\rightarrow\infty}$ on both sides of this inequality, we are led to contradiction.

On the other hand, let $\upsilon^{\prime} ( t ) >0$ for all $t\geq t_{1}$. The proof of this case is similar to that of Theorem 2.7, and so we omit it. Then the proof is complete. □

Example 2.1

Consider the equation

$$ \bigl( t^{2\alpha} \bigl[ \bigl( u ( t ) +p_{0}u ( \lambda t ) \bigr) ^{\prime} \bigr] ^{\alpha} \bigr) ^{ \prime}+q_{0}t^{\gamma-1}u^{\beta} ( \delta t ) =0, $$

(2.44)

where $\alpha>0$, $\lambda,\delta\in(0,1)$, $p_{0}\in{}[ 0,\lambda)$, $q_{0}>0$, and $\gamma=\max \{ \alpha,\beta \}$. We note that

$$ r ( t ) :=t^{2\alpha},\qquad p ( t ) :=p_{0},\qquad \tau( t ) :=\lambda t,\qquad \sigma( t ) := \delta t,\qquad q ( t ) :=q_{0}t^{\gamma-1}, $$

and $f ( u ) =u^{\beta}$. It is easy to calculate that

$$ \pi( t ) =\frac{1}{t}\quad \text{and}\quad Q ( t ) =q_{0} \biggl( 1-\frac{p_{0}}{\lambda} \biggr) ^{\beta}t^{\gamma-1}. $$

From Theorem 2.3, equation (2.44) is oscillatory if the first order delay differential equation

$$ \upsilon^{\prime} ( t ) +\frac{K}{t^{2-\gamma/\alpha}} \upsilon ^{\beta/\alpha} ( \delta t ) =0 $$

is oscillatory, where

$$ K= \biggl( \frac{q_{0}}{\gamma} \biggl( 1-\frac{p_{0}}{\lambda} \biggr) ^{\beta} \biggr) ^{1/\alpha}>0. $$

For$\alpha>\beta$, we see that $\gamma=\alpha$ and hence

$$ \int_{t_{0}}^{\infty}\frac{K}{t^{2-\gamma/\alpha}}\,\mathrm{d}\nu = \infty. $$

Then, by Corollary 2.2, equation (2.44) is oscillatory.

For$\alpha<\beta$, we have (2.13) holds if

$$ q_{0} \biggl( 1-\frac{p_{0}}{\lambda} \biggr) ^{\beta}a_{2}> \beta. $$

But this condition is not feasible as a result of constant $a_{2}$. However, according to Theorem 2.2, if we take $\gamma=\beta+1$, then (2.13) holds and hence equation (2.44) is oscillatory.

For$\alpha=\beta$, we have the following criteria for oscillation:

• By Theorem 2.2, we get the condition

  

• By Corollary 2.1, we get the condition

  

• By Theorem 2.6, we get the condition

  

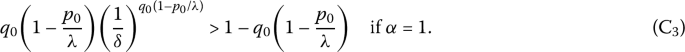
• By Theorem 2.8 with $\delta ( t ) :=t^{-\alpha}$, we have that condition (2.41) holds if

  

As special cases, we consider the equations

and

From Table 1, we note that Condition ($\mathrm {C}_{4}$) supports the most efficient condition for ($\mathrm {E}_{1}$) and Condition ($\mathrm {C}_{2}$) supports the most efficient condition for ($\mathrm {E}_{2}$).

Table 1 Test of the strength of criteria for ($\mathrm {E}_{1}$) and ($\mathrm {E}_{2}$)

Moreover, for ($\mathrm {E}_{1}$), we see that Condition ($\mathrm {C}_{3}$) provides an improvement of Conditions ($\mathrm {C}_{1}$) and ($\mathrm {C}_{2}$), namely $q_{0}>0.8532$.

Also, for Euler differential equation, if $p_{0}=0$ and $\alpha=1$, then condition ($\mathrm {C}_{4}$) reduces to $q_{0}>1/4$, which is sharp for oscillation.