Nonlocal controllability of fractional measure evolution equation

Abstract

In this paper, we consider the following kind of fractional evolution equation driven by measure with nonlocal conditions:

$$ \textstyle\begin{cases} {}^{C} D_{0+}^{\alpha }x(t)=Ax(t)\,dt+ (f(t,x(t))+Bu(t) )\,dg(t), \quad t\in (0, b],\\ x(0)+p(x)=x_{0}. \end{cases} $$

The regulated proposition of fractional equation is obtained for the first time. By noncompact measure method and fixed point theorems, we obtain some sufficient conditions to ensure the existence and nonlocal controllability of mild solutions. Finally, an illustrative example is given to show practical usefulness of the analytical results.

1 Introduction

Measure driven equations were investigated firstly in [1, 2], and they can permit an infinite number of discontinuous points in a finite time interval, so it is convenient to model discontinuous dynamical systems. Differential equations and difference equations are special cases of measure differential equations. One can refer to [3, 4] for the applications of measure differential equations such as modeling the quantum. Some recent papers have investigated the existence of solutions for measure differential equations (see [5–8]).

In recent years, along with multiple phenomena arising in physics, biophysics, engineering, science, etc., fractional calculus as an important tool has been used in different areas (see [9–15] and the references therein). Fractional derivative is simple in modeling, clear in physical meaning of parameters, and accurate in description. Fractional derivative operators can concisely and accurately describe mechanical and physical processes with historical memory and spatial global correlation, which has attracted the attention of many scholars. Referring to [16–31], we will obtain more details about theory and application of fractional differential equations.

Recently the theory of controllability has attracted many authors, e.g., [32–34]. Wan and Sun considered the approximate controllability for abstract measure differential systems (see [35]), Cao and Sun in [36] discussed the complete controllability of measure differential equations by using Monch fixed point theorem and noncompact measure. Measure differential equation has developed rapidly, but it mainly focuses on integer order, there are few results on fractional order.

Inspired by the above discussion, in this paper, we investigate a kind of fractional evolution equations driven by measure with nonlocal conditions. If g is an absolutely continuous function, then Eq. (1.1) becomes a fractional evolution equation; if g is the sum of an absolutely continuous function with a step function, then Eq. (1.1) becomes an impulsive fractional evolution equation. So fractional evolution equations driven by measure are more general. Since fractional measure differential equations are not as continuous or smooth as ordinary differential equations, they are only right continuous and bounded, this brings some difficulties to the further study of them. In order to solve this problem, we prove the regulated proposition of fractional equation for the first time. By noncompact measure method and fixed point theorems, we obtain some sufficient conditions to ensure the existence and nonlocal controllability of mild solutions. If the infinitesimal generator operator is noncompact, similar results can also be derived.

In this paper, we consider the following fractional measure evolution differential equation with nonlocal conditions:

$$ \textstyle\begin{cases} {}^{C} D_{0+}^{\alpha }x(t)=Ax(t)\,dt+ (f(t,x(t))+Bu(t) )\,dg(t), \quad t\in (0, b], \\ x(0)+p(x)=x_{0}, \end{cases} $$

(1.1)

where $0<\alpha < 1$, ${}^{C} D_{0+}^{\alpha }$ is a Caputo derivative of order α, A is a closed densely defined linear operator, $f:[0, b]\times X \rightarrow X$, X is a Banach space, $p(x):G([0, b];X) \rightarrow X$ is a specified function. The set $G([0, b];X)$ is a space of regulated functions on $[0, b]$, which will be given later. The control function $u(\cdot )$ takes values in $U_{ad}$, where $U_{ad}$ is a control set. $g:[0, b] \rightarrow \mathbb{R}$ is a left continuous nondecreasing function.

The rest of the paper is organized as follows. Section 2 introduces some fundamentals that will be used later. In Sect. 3, we derive the existence result for fractional measure evolution Eq. (1.1) by means of Darbo–Sadovskii’s fixed point theorem and noncompact measure. In Sect. 4, by Krasnoselskii’s fixed point theorem, we obtain the controllability results for fractional measure evolution Eq. (1.1); if the infinitesimal generator operator is noncompact, similar results can also be derived. An illustrative example is given to show the practical usefulness of the analytical results in Sect. 5.

2 Preliminaries

In this section, we recall some basic concepts which will be used in what follows.

Let $K=[0, b]$. A finite collection of system $\{(\xi _{i},I_{i}):i=1,2,\ldots,n\}$ is called a partition of $[0,b)$ if $\bigcup^{n}_{i=1}I_{i}=[0,b)$, where the intervals $I_{i}$ are nonoverlapping, $\xi _{i} \in I_{i}$. For a given gauge δ on $[0,b)$, we say that a partition $\{(\xi _{i},I_{i}):i=1,2,\ldots,n\}$ is δ-fine if $I_{i}\subset [\xi _{i}-\delta (\xi _{i}),\xi _{i}+\delta (\xi _{i}) )$, $i=1,2,\ldots,n$.

Definition 2.1

(Regulated function, see [8])

If a function $f:K \rightarrow X$ satisfies the limits

$$ \lim_{s \rightarrow t^{-}}f(s)=f\bigl(t^{-}\bigr),\quad t \in (0,b]\quad \text{and}\quad \lim_{s \rightarrow t^{+}}f(s)=f \bigl(t^{+}\bigr),\quad t \in [0,b), $$

then the function f is called regulated function on K.

By $G(K;X)$ we denote the Banach space of all regulated functions with the norm $\|f\|_{\infty }=\sup_{t\in K}\|f(t)\|$, and the set of discontinuous points of a regulated function is at most countable.

Definition 2.2

(Henstock–Lebesgue–Stieltjes integration, see [8])

A function $f:[0, b]\rightarrow X$ is called Henstock–Lebesgue–Stieltjes integrable over $[0, b)$ if there is a function denoted by $(\mathit{HLS})\int _{0}^{\cdot }:[0,b]\rightarrow X$ such that, given $\varepsilon >0$, there exists a gauge $\delta _{\varepsilon }$ on $[0, b)$ with

$$ \sum^{n}_{i=1} \biggl\Vert f(\xi _{i}) \bigl(g(t_{i})-g(t_{i-1}) \bigr) - \biggl((\mathit{HLS}) \int _{0}^{t_{i}}f(s)\,dg(s) -(\mathit{HLS}) \int _{0}^{t_{i-1}}f(s)\,dg(s) \biggr) \biggr\Vert < \varepsilon $$

for every $\delta _{\varepsilon }$-fine partition $\{(\xi _{i},[t_{i-1},t_{i})):i=1,2,\ldots,n\}$ of $[0, b)$.

Let $\mathit{HLS}^{p}_{g}(K;X)$ ($p>1$) be a space of all p-ordered Henstock–Lebesgue–Stieltjes integral regulated functions from K to X with respect to g, with the norm $\|\cdot \|_{\mathit{HLS}_{g}^{p}}$ defined by

$$ \Vert f \Vert _{\mathit{HLS}_{g}^{p}}= \biggl((\mathit{HLS}) \int _{0}^{b} \bigl\Vert f(s) \bigr\Vert ^{p}\,dg(s) \biggr)^{ \frac{1}{p}}. $$

Let Y be another separable reflexive Banach space where control function u takes values. Let $E\subset Y$ be bounded, and the admissible control set $U_{ad}= \mathit{HLS}^{p}_{g}(K;E)$, $p>1$.

Proposition 2.3

Consider the functions$f\in \mathit{HLS}^{p}_{g}(K;X)$ ($p>1$) and$g:K \rightarrow \mathbb{R}$satisfying thatgis regulated. Then the function

$$ j(t)=(\mathit{HLS}) \int ^{t}_{0}(t-s)^{\alpha -1}f(s) \,dg(s),\quad t \in K $$

is regulated and satisfies

$$\begin{aligned}& j(t)-j\bigl(t^{-}\bigr)\leq \biggl( \int _{t^{-}}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} f(t) \bigl(\triangle ^{-}g(t)\bigr)^{ \frac{1}{p}},\quad t \in (0, b], \\& j\bigl(t^{+}\bigr)-j(t)\leq \biggl( \int _{t}^{t^{+}}\bigl[\bigl(t^{+}-s \bigr)^{ \alpha -1}\bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} f(t) \bigl(\triangle ^{+}g(t)\bigr)^{ \frac{1}{p}},\quad t \in [0, b), \end{aligned}$$

where$q>1$, $\frac{1}{p}+\frac{1}{q}=1$, $\triangle ^{+}g(t)=g(t^{+})-g(t)$, $\triangle ^{-}g(t)=g(t)-g(t^{-})$, $g(t^{+})$and$g(t^{-})$denote the right and left limits of functiongat pointt.

Proof

Claim I: We prove that the function $j(t)$ is regulated, i.e., $\lim_{\tau \rightarrow t^{-} }j(\tau )=j(t^{-})$, $t\in (0,b]$. The other direction can be proved in a similar way. For this purpose, we consider

$$\begin{aligned}& \bigl\vert j(t)-j\bigl(t^{-}\bigr) \bigr\vert \\& \quad = \biggl\vert (\mathit{HLS}) \int _{0}^{t}(t-s)^{\alpha -1}f(s)\,dg(s) -(\mathit{HLS}) \int _{0}^{t^{-}}\bigl(t^{-}-s \bigr)^{\alpha -1}f(s)\,dg(s) \biggr\vert \\& \quad \leq \biggl\vert (\mathit{HLS}) \int _{t^{-}}^{t}(t-s)^{\alpha -1}f(s)\,dg(s) \biggr\vert \\& \qquad {} + \biggl\vert (\mathit{HLS}) \int _{0}^{t^{-}} \bigl((t-s)^{\alpha -1}- \bigl(t^{-}-s\bigr)^{ \alpha -1} \bigr)f(s)\,dg(s) \biggr\vert \\& \quad \leq \biggl( \int _{t^{-}}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{t^{-}}^{t}\bigl(f(s)\bigr)^{p} \,dg(s) \biggr)^{ \frac{1}{p}} \\& \qquad {} + \biggl\vert (\mathit{HLS}) \int _{0}^{t^{-}} \bigl((t-s)^{\alpha -1}- \bigl(t^{-}-s\bigr)^{ \alpha -1} \bigr)f(s)\,dg(s) \biggr\vert . \end{aligned}$$

By the definition of Henstock–Lebesgue–Stieltjes integration, we have

$$ \biggl( \int _{t^{-}}^{t}\bigl(f(s)\bigr)^{p} \,dg(s) \biggr)^{\frac{1}{p}} = f(t) \bigl(g(t)-g\bigl(t^{-}\bigr) \bigr)^{\frac{1}{p}}. $$

In terms of the regulated proposition of g and dominated convergence theorem, one has

$$ \bigl\vert j(t)-j\bigl(t^{-}\bigr) \bigr\vert \leq \biggl( \int _{t^{-}}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} f(t) \bigl(g(t)-g \bigl(t^{-}\bigr) \bigr)^{\frac{1}{p}}. $$

Claim II: As the proof of Claim I, we can easily derive the following inequality:

$$ j\bigl(t^{+}\bigr)-j(t)\leq \biggl( \int _{t}^{t^{+}}\bigl[\bigl(t^{+}-s \bigr)^{\alpha -1}\bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} f(t) \bigl(\triangle ^{+}g(t)\bigr)^{\frac{1}{p}},\quad t \in [0, b). $$

This completes the proof. □

Definition 2.4

(Equiregulated set, see [8])

A set $D \subset G(K;X)$ is called equiregulated if there is $\nu >0$; for every $t_{0}\in K$ and $\epsilon >0$, we have

• (i) If $x \in D$, $t \in K$ and $t_{0}-\nu < t< t_{0}$, then $\| x(t_{0}^{-})-x(t)\|<\epsilon$;

• (ii) If $x \in D$, $t \in K$ and $t_{0} < t< t_{0}+\nu$, then $\| x(t)-x(t_{0}^{+})\|<\epsilon$.

Lemma 2.5

(Uniform convergence, see [8])

Let$\{ x_{n}\}^{\infty }_{n=1}$be a sequence of functions fromKtoX. If the sequence$\{x_{n}\}^{\infty }_{n=1}$is equiregulated and$x_{n}$converges pointwisely to$x_{0}$as$n \rightarrow \infty$, then$x_{n}$converges uniformly to$x_{0}$.

Definition 2.6

(Riemann–Liouville integral and derivative)

The Riemann–Liouville fractional integral and derivative are defined respectively by

$$ I_{0+}^{\alpha }x(t)=l_{\alpha }(t)\ast x(t)= \int _{0}^{t}l_{\alpha }(t-s)x(s)\,ds, \quad t>0, $$

and

$$ ^{L}\!D_{0+}^{\alpha }x(t)=\frac{d^{n}}{dt^{n}} \bigl(l_{n-\alpha }(t) \ast x(t) \bigr), $$

where ∗ denotes the convolution,

$$ l_{\alpha }(t)=\frac{t^{\alpha -1}}{\varGamma (\alpha )}, $$

$x\in C([0,\infty ),X)$, $\alpha >0$, $n=[\alpha ]+1$.

Definition 2.7

(Caputo derivative)

The Caputo derivative of order $\alpha >0$ for a function $x\in C([0, \infty ],X)$ is defined as

$$ {}^{C} D_{0+}^{\alpha }x(t)=l_{n-\alpha }(t) \ast \frac{d^{n}x(t)}{dt^{n}}, $$

where $n=[\alpha ]+1$.

Now, we introduce the Hausdorff noncompact measure $\sigma (\cdot )$ defined on each bounded subset Ω of Banach space X by

$$ \sigma (\varOmega )=\inf \{\epsilon >0, \varOmega \text{ has a finite } \epsilon \text{-net in } X\}. $$

ϵ-net: Let $M\subset (X,\rho )$, $\epsilon >0$, $N\subset M$, if for all $x\in M$, $\exists y\in N$ satisfies $\rho (x,y)<\epsilon$, then N is a ϵ-net of M. If N is finite, then N is a finite ϵ-net of M, where $(X,\rho )$ is a metric space. For more details, see [37]. Some basic properties of $\sigma (\cdot )$ are given in the following lemmas.

Lemma 2.8

(see [37])

The noncompact measure$\sigma (\cdot )$satisfies:

• (i) $\sigma (B)=0$if and only ifBis relatively compact inX;

• (ii) if$\sigma (\{x\}\cup B)=\sigma ( B)$for every$x\in X$and every nonempty subset$B\subseteq X$;

• (iii) $\sigma (\lambda B)\leq |\lambda | \sigma (B)$for any$\lambda \in \mathbb{R}$;

• (iv) $\sigma (B_{1}+B_{2})\leq \sigma (B_{1})+\sigma (B_{2})$, where$B_{1}+B_{2}=\{x+y: x\in B_{1},y\in B_{2}\}$;

• (v) $\sigma (B_{1}\cup B_{2})\leq \max \{\sigma (B_{1}),\sigma (B_{2})\}$.

Since the Lebesgue–Stieltjes measure is a regular Borel measure, then we refer to Theorem 3.1 in [38], the following result can be derived.

Theorem 2.9

Let$R_{0}\subset \mathit{HLS}_{g}^{1}(K,X)$be a countable set. Assume that there is a positive function$\nu \in \mathit{HLS}_{g}^{1}(K,\mathbb{R}^{+})$such that$\|r(t)\|\leq \nu (t)$holds for all$r(t) \in R_{0}$. Then we have

$$ \sigma \biggl( \int _{K}R_{0}(t)\,dg(t) \biggr)\leq 2 \int _{K}\sigma \bigl(R_{0}(t)\bigr)\,dg(t). $$

Theorem 2.10

(Darbo–Sadovskii fixed point, see [37])

If$D\subset X$is a convex bounded and closed set, the continuous mapping$Z:D\rightarrow D$is aσ-contraction, thenZhas at least one fixed point inD.

Theorem 2.11

(Krasnoselskii fixed point, see [39])

If$B\subset X$is bounded closed and convex, whereXis a Banach space, operators$P:D \rightarrow X$and$Q:D \rightarrow X$satisfy the following conditions:

• (i) $Px+Qy \in D$whenever$x,y \in D$;

• (ii) Pis a compact and continuous mapping;

• (iii) Qis a contraction operator.

Then$P+Q$has a fixed point inD.

Referring to the definition of mild solution given in [21, 40], we define the mild solution for fractional measure evolution Eq. (1.1) in the space of regulated function $G(K; X)$ as follows.

Definition 2.12

A function $x \in G(K; X)$ is said to be a mild solution of problem (1.1) if it satisfies

$$ x(t)=T_{\alpha }(t) \bigl(x_{0}-p(x)\bigr) + \int _{0}^{t}(t-s)^{\alpha -1}S_{ \alpha }(t-s) \bigl(f\bigl(s,x(s)\bigr)+Bu(s) \bigr)\,dg(s), $$

for $t \in K$, where

$$ T_{\alpha }= \int _{0}^{\infty }\eta _{\alpha }(\theta )T \bigl(t^{\alpha } \theta \bigr)\,d \theta ,\qquad S_{\alpha }=\alpha \int _{0}^{\infty }\theta \eta _{ \alpha }( \theta )T\bigl(t^{\alpha }\theta \bigr)\,d \theta , $$

$A:D(A)\subseteq X \rightarrow$ is the infinitesimal generator of equicontinuous $C_{0}$-semigroup $T(t)$, $\eta _{\alpha }$ is a probability density function defined on $(0, \infty )$, that is, $\eta _{\alpha }(t)\geq 0$, $\theta \in (0,\infty )$ and $\int ^{\infty }_{0}\eta _{\alpha }(\theta )\,d \theta =1$.

Lemma 2.13

(see [40])

$T_{\alpha }$, $S_{\alpha }$have the following properties:

• (i) For every fixed$t\geq 0$, the operators$T_{\alpha }$and$S_{\alpha }$are all linear and bounded, i.e., for each$x \in X$,

  $$ \bigl\Vert T_{\alpha }(t)x \bigr\Vert \leq M_{1} \Vert x \Vert ,\qquad \bigl\Vert S_{\alpha }(t)x \bigr\Vert \leq \frac{M_{1}}{\varGamma (\alpha )} \Vert x \Vert . $$

  The operators$T_{\alpha }$and$S_{\alpha }$are all compact if$T(t)$ ($t>0$) is compact for any$t\geq 0$.

• (ii) $T_{\alpha }$and$S_{\alpha }$are all strongly continuous operators.

3 Existence of solution

In this section, by using the measure of noncompactness and fixed point theorem, we obtain a sufficient condition in order to ensure the existence of a mild solution.

The following hypotheses will be used:

• (H1) The $C_{0}$-semigroup $T(t)$ generated by a linear operator $A:D(A)\subseteq X \rightarrow X$ is compact for $t>0$.

• (H2) The function $f:K \times X \rightarrow X$:

  • (i) $f(\cdot ,x)$ is measurable for all $x \in X$, and $f(t, \cdot )$ is continuous for a.e. $t \in K$;

  • (ii) There is a function $h\in \mathit{HLS}^{p}_{g}(K;\mathbb{R}^{+})$ and a nondecreasing continuous function $\varPhi :\mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$ such that

    $$ \bigl\Vert f(t,x) \bigr\Vert \leq h(t)\varPhi \bigl( \Vert x \Vert \bigr) $$

    for all $x \in X$, almost all $t \in K$, and

    $$ \liminf_{l\rightarrow +\infty }\frac{\varPhi (l)}{l}=\varphi < +\infty . $$

• (H3) $p:G(K;X)\rightarrow X$ is a continuous and compact mapping, and there are two positive constants c and d such that $\| p(x)\|\leq c\|x\|_{\infty }+d$ for all $x\in G(K;X)$.

• (H4) $B:E\to X$ is a linear and bounded operator, so there is a positive constant $M_{2}$ such that

  $$ \Vert B \Vert \leq M_{2}. $$

• (H5) The control function u is given in $U_{ad}$, a Banach space of admissible control functions.

Theorem 3.1

Suppose that hypotheses (H1)–(H5) are satisfied, then the fractional measure evolution Eq. (1.1) has at least one solution on$(0,b]$provided that

$$ M_{1}c+\varphi \sup_{t\in [0,b]}{ \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}}}\frac{M_{1}}{\varGamma (\alpha )} \Vert h \Vert _{\mathit{HLS}_{g}^{p}}< 1. $$

(3.1)

Proof

Let $r \geq 0$ and $B_{r}=\{G(K;X):\|x\|_{\infty }< r\}$, we denote $\overline{B_{r}}=\{G(K;X):\|x\|_{\infty }\leq r\}$. Define the operators F, $F_{1}$, $F_{2}$ as follows:

$$\begin{aligned}& Fx(t)=T_{\alpha }(t) \bigl(x_{0}-p(x)\bigr) + \int _{0}^{t}(t-s)^{\alpha -1}S_{ \alpha }(t-s) \bigl(f\bigl(s,x(s)\bigr)+Bu(s)\bigr)\,dg(s), \\& F_{1}x(t)=T_{\alpha }(t) \bigl(x_{0}-p(x)\bigr), \\& F_{2}x(t)= \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s) \bigl(f\bigl(s,x(s)\bigr)+Bu(s)\bigr)\,dg(s). \end{aligned}$$

The proof process is divided into four steps.

Step I. We can find a positive number r such that $F(\overline{B_{r}})\subseteq \overline{B_{r}}$.

If this is not the case, there is a function $x_{r}$ satisfying $\|F(x_{r})(t)\|>r$ for some $t \in K$. According to assumptions (H1)–(H4), we get

$$\begin{aligned} r< {}& \bigl\Vert F(x_{r}) (t) \bigr\Vert \\ ={}& \biggl\Vert T_{\alpha }(t) \bigl(x_{0}-p(x_{r}) \bigr) + \int _{0}^{t}(t-s)^{ \alpha -1}S_{\alpha }(t-s)f \bigl(s,x_{r}(s)\bigr)\,dg(s) \\ &{}+ \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)Bu(s) \,dg(s) \biggr\Vert \\ \leq{} & M_{1}\bigl( \Vert x_{0} \Vert +cr+d\bigr) \\ &{} +\frac{M_{1}}{\varGamma (\alpha )} \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{0}^{b} \bigl\Vert f \bigl(s,x_{r}(s)\bigr) \bigr\Vert ^{p}\,dg(s) \biggr)^{\frac{1}{p}} \\ &{}+ \bigl\Vert S_{\alpha }(t-s)B \bigr\Vert \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{0}^{b} \bigl\Vert u(s) \bigr\Vert ^{p}\,dg(s) \biggr)^{\frac{1}{p}} \\ \leq {}& M_{1}\bigl( \Vert x_{0} \Vert +cr+d\bigr) \\ & {} +\sup_{t\in [0,b]}{ \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}}} \biggl( \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \Vert h \Vert _{\mathit{HLS}_{g}^{p}} + \frac{M_{1}M_{2} \Vert u \Vert _{\mathit{HLS}}}{\varGamma (\alpha )} \biggr). \end{aligned}$$

We can divide both sides of this inequality by r and take the limit $r\rightarrow +\infty$ in both sides to get

$$ 1\leq M_{1}c+\varphi \sup_{t\in [0,b]}{ \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}}} \frac{M_{1}}{\varGamma (\alpha )} \Vert h \Vert _{\mathit{HLS}_{g}^{p}}, $$

which contradicts (3.1), so we can find r satisfying $F(\overline{B_{r}})\subseteq \overline{B_{r}}$.

Step II. F is continuous on $\overline{B_{r}}$.

Let $x^{n} \rightarrow x \in \overline{B_{r}}$ as $n\rightarrow \infty$, where $\{x^{n}\}^{\infty }_{n=1}$ is a sequence in $\overline{B_{r}}$. Then we have

$$\begin{aligned}& \bigl\Vert F\bigl(x^{n}\bigr) (t)-F(x) (t) \bigr\Vert \\& \quad \leq \bigl\Vert T_{\alpha }(t) \bigr\Vert \bigl\Vert p \bigl(x^{n}\bigr)-p(x) \bigr\Vert \\& \qquad {} + \biggl\Vert \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)f \bigl(s,x^{n}\bigr)\,dg(s)- \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)f \bigl(s,x(s)\bigr)\,dg(s) \biggr\Vert \\& \quad \leq M_{1} \bigl\Vert \bigl(p\bigl(x^{n} \bigr)-p(x)\bigr) \bigr\Vert + \frac{M_{1}}{\varGamma (\alpha )} \int _{0}^{t}(t-s)^{\alpha -1} \bigl\Vert f\bigl(s,x^{n}(s)\bigr)-f\bigl(s,x(s)\bigr) \bigr\Vert \,dg(s). \end{aligned}$$

From the continuity of $p(x)$ and (H2)(i), we derive that the operator $F:\overline{B_{r}} \rightarrow \overline{B_{r}}$ is continuous.

Step III. $F(\overline{B_{r}})$ is equiregulated on K.

For any $t_{0}\in [0,b)$, we get

$$\begin{aligned}& \bigl\Vert F(x) (t)-F(x) \bigl(t_{0}^{+}\bigr) \bigr\Vert \\& \quad \leq \bigl\Vert \bigl(T_{\alpha }(t)-T_{\alpha } \bigl(t_{0}^{+}\bigr) \bigr) \bigl(x_{0}-p(x) \bigr) \bigr\Vert \\& \qquad {}+ \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}S_{ \alpha }(t-s)-\bigl(t_{0}^{+}-s \bigr)^{\alpha -1}S_{\alpha }\bigl(t_{0}^{+}-s \bigr) \bigr)f\bigl(s,x(s)\bigr) \bigr\Vert \,dg(s) \\& \qquad {}+ \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}S_{ \alpha }(t-s)f \bigl(s,x(s)\bigr) \bigr\Vert \,dg(s) \\& \qquad {}+ \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}S_{ \alpha }(t-s)-\bigl(t_{0}^{+}-s \bigr)^{\alpha -1}S_{\alpha }\bigl(t_{0}^{+}-s \bigr) \bigr)Bu(s) \bigr\Vert \,dg(s) \\& \qquad {}+ \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}S_{\alpha }(t-s)Bu(s) \bigr\Vert \,dg(s) \\& \quad = A_{1}+A_{2}+A_{3}+A_{4}+A_{5}, \end{aligned}$$

where

$$\begin{aligned}& A_{1}= \bigl\Vert \bigl(T_{\alpha }(t)-T_{\alpha } \bigl(t_{0}^{+}\bigr) \bigr) \bigl(x_{0}-p(x) \bigr) \bigr\Vert , \\& A_{2}= \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}S_{\alpha }(t-s)-\bigl(t_{0}^{+}-s \bigr)^{ \alpha -1}S_{\alpha }\bigl(t_{0}^{+}-s \bigr) \bigr)f\bigl(s,x(s)\bigr) \bigr\Vert \,dg(s), \\& A_{3}= \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}S_{\alpha }(t-s)f \bigl(s,x(s)\bigr) \bigr\Vert \,dg(s), \\& A_{4}= \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}S_{\alpha }(t-s)-\bigl(t_{0}^{+}-s \bigr)^{ \alpha -1}S_{\alpha }\bigl(t_{0}^{+}-s \bigr) \bigr)Bu(s) \bigr\Vert \,dg(s), \\& A_{5}= \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}S_{\alpha }(t-s)Bu(s) \bigr\Vert \,dg(s). \end{aligned}$$

In terms of conditions (H2) and (H3) we know that the sets $\{p(x):x \in \overline{B_{r}}\}$ and $\{f(s,x(s)): s\in K, x \in \overline{B_{r}}\}$ are bounded. Moreover, according to the compactness and strong continuity of $T(t)$, we know $T(t)$ satisfies uniform operator topology continuity, and applying dominated convergence theorem, we can derive that $A_{1}$, $A_{2}$, $A_{4}$ all tend to zero independently of x as $t \rightarrow t_{0}^{+}$. Let $j(t)=\int _{0}^{t}k_{\alpha }(s)\,dg(s)$, where $k_{\alpha }(s)=(t-s)^{\alpha -1}h(s)$, referring to Proposition 2.3, $j(t):K \rightarrow X$ is a regulated function, we can obtain

$$\begin{aligned} A_{3}&\leq \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}h(s) \bigr\Vert \,dg(s) \\ &\leq \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \biggl( \bigl\Vert j(t)-j \bigl(t_{0}^{+}\bigr) \bigr\Vert + \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}-\bigl(t_{0}^{+}-s \bigr)^{ \alpha -1} \bigr)f(s) \bigr\Vert \,dg(s) \biggr), \end{aligned}$$

when $t \rightarrow t_{0}^{+}$, we have $A_{3}\rightarrow 0$. In a similar way, we know that $A_{5}\rightarrow 0$ as $t \rightarrow t_{0}^{+}$. According to the above discussion, we can also derive that $\|F(x)(t_{0}^{-})-F(x)(t) \|\rightarrow 0$ as $t \rightarrow t_{0}^{-}$ for every $t_{0} \in (0,b]$. So $F(\overline{B_{r}})$ is equiregulated on K.

Step IV. F is a contraction mapping.

In fact, for $x, y\in \overline{B_{r}}$, $0< t< b$, we have

$$\begin{aligned} \bigl\Vert F_{1}(x) (t)-F_{1}(y) (t) \bigr\Vert &\leq \bigl\Vert T_{\alpha }(t) \bigl(p(x)-p(y) \bigr) \bigr\Vert \\ &\leq cM_{1} \Vert x-y \Vert , \end{aligned}$$

so for any bounded $D\subset \overline{B_{r}}$, we have $\sigma (F_{1}D)\leq cM_{1}\sigma (D)$.

In the following we prove that $F_{2}$ is a compact operator.

In terms of Step II, we know that $\lim F_{2}x^{n}=F_{2}x$ as $n\rightarrow \infty$, $F_{2}$ is continuous on $\overline{B_{r}}$.

Let t be fixed, where $t \in K$, ϕ is a positive constant and satisfies $0<\phi \leq t$ for each $F_{2}x(\cdot )\in \overline{B_{r}}$,

$$ F_{2\phi }x(t)=S_{\alpha }(\phi ) \int _{0}^{t-\phi }(t-s)^{\alpha -1}S_{ \alpha }(t-s- \phi ) \bigl(f\bigl(s, x(s)\bigr)+Bu(s) \bigr)\,dg(s). $$

It follows from the compactness of $S_{\alpha }$ that the set $F_{2\phi }x(t)=\{F_{2\phi }x(t):x(\cdot )\in \overline{B_{r}}\}$ is relatively compact in X for each $0<\phi <t$. On the other hand, for any $x(\cdot )\in \overline{B_{r}}$, under condition (H2), we have

$$\begin{aligned} \bigl\Vert F_{2}x(t)-F_{2\phi }x(t) \bigr\Vert &= \biggl\Vert \int _{t-\phi }^{t}(t-s)^{ \alpha -1}S_{\alpha }(t-s- \phi )f\bigl(s, x(s)\bigr)\,dg(s) \biggr\Vert \\ &\leq \frac{M_{1}}{\varGamma (\alpha )} \int _{t-\phi }^{t}(t-s)^{ \alpha -1} \bigl\Vert f\bigl(s, x_{r}(s)\bigr) \bigr\Vert \,dg(s) \\ & \leq \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \int _{t- \phi }^{t}(t-s)^{\alpha -1}h(s)\,dg(s). \end{aligned}$$

According to hypothesis (H2), we know that $\int _{t-\phi }^{t}(t-s)^{\alpha -1}h(s)\,dg(s)$ is regulated and continuous from the left, then the last inequality tends to zero as $\phi \rightarrow 0^{+}$. So, for each $t\in K$, $F_{2}$ is relatively compact on $\overline{B_{r}}$ for any $D\subset \overline{B_{r}}$, we obtain that

$$ \sigma (FD)\leq \sigma (F_{1}D)+\sigma (F_{2}D)\leq cM_{1}\sigma (D). $$

By (3.1) we know $cM_{1}<1$, so the operator F is condensed.

According to Darbo–Sadovskii’s fixed point theorem, we know that the fractional measure evolution problem (1.1) has a solution on the interval K. This completes the proof. □

Remark 3.1

If g is a step function $g(s)=\sum^{\infty }_{n=1}\rho _{n}\varTheta (s-t_{n})$, where $t_{1}< t_{2}<\cdots$ is a sequence of moments in $[0,b]$, $\sum^{\infty }_{n=1}\rho _{n}< \infty$, where $(\rho _{n})_{n}$ is a sequence of positive numbers, and $\varTheta (s-t_{n})=0$ if $s\leq 0$; otherwise $\varTheta (s-t_{n})=1$, $\varTheta (s-t_{n})$ is a singular function, then Eq. (1.1) becomes a fractional evolution equation.

Remark 3.2

If g is the sum of an absolutely continuous function with a step function as in Remark 3.1, then Eq. (1.1) becomes an impulsive fractional evolution equation.

4 Nonlocal controllability

In this section, we obtain some sufficient conditions ensuring the nonlocal controllability of mild solutions by employing the measure of noncompactness and fixed point theorem.

Definition 4.1

(Nonlocally controllable, see [36])

If for each $x_{0},x_{1}\in X$ there is a control $u \in U_{ad}$ such that the mild solution $x(\cdot )$ of (1) satisfies that $x(b)+q(x)=x_{1}$, then system (1.1) is said to be nonlocally controllable on K.

Furthermore, we suppose that

• (H6) There is a function $W\in \mathit{HLS}^{p}_{g}(K;\mathbb{R}^{+})$ ($p>1$) such that

  $$ \sigma \bigl(f(t,D)\bigr)\leq W(t)\sigma (D). $$

• (H7) Define an operator $\varLambda \in \mathit{HLS}^{p}_{g}(K;X)$ ($p>1$) by

  $$ \varLambda u= \int ^{b}_{0}(b-s)^{\alpha -1}S_{\alpha }(b-s)Bu(s) \,dg(s), $$

  and assume it satisfies the following:

  • (i) Operator $\varLambda ^{-1}$ taking value in $\mathit{HLS}^{p}_{g}(K;X)/\ker \varLambda$ exists and there is a positive constant $M_{3}$ such that

    $$ \bigl\Vert \varLambda ^{-1} \bigr\Vert \leq M_{3}; $$

  • (ii) There is a function $J\in \mathit{HLS}^{p}_{g}(K;\mathbb{R}^{+})$ ($p>1$) such that, for almost $t\in K$ and any bounded set $D\subseteq X$,

    $$ \sigma \bigl(\bigl(\varLambda ^{-1}D\bigr) (t)\bigr)\leq J(t)\sigma (D). $$

Theorem 4.2

Suppose that hypotheses (H1)–(H7) are satisfied, then the fractional measure evolution Eq. (1.1) is controllable on$(0,b]$if

$$ \begin{gathered}[b] c \biggl(M_{1}+\frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha )}(1+M_{1}) \biggr) \\ \quad {} +\frac{M_{1}\gamma }{\varGamma (\alpha )}\sup_{t\in [0,b]}{ \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}}} \biggl(1+ \frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha ) } \biggr) \Vert h \Vert _{\mathit{HLS}_{g}^{p}}< 1 \end{gathered} $$

(4.1)

and

$$\begin{aligned} \varXi =& \biggl( \frac{4M_{1}^{2}M_{2}}{\varGamma (\alpha )^{2}}\sup_{t\in [0,b]} \int _{0}^{t}(t-s)^{ \alpha -1}J(s)\,dg(s) +\frac{2M_{1}}{\varGamma (\alpha )} \biggr) \\ &{} \times \sup_{t\in [0,b]} \int _{0}^{t}(t-s)^{\alpha -1}W(s)\,dg(s)< 1. \end{aligned}$$

Proof

Let $x_{0}\in X$ be fixed. Define the operators F, $F_{1}$, $F_{2}$ as follows:

$$\begin{aligned}& Fx(t)= T_{\alpha }(t) \bigl(x_{0}-p(x)\bigr) + \int _{0}^{t}(t-s)^{ \alpha -1}S_{\alpha }(t-s) \bigl(f\bigl(s,x(s)\bigr)+Bu(s) \bigr)\,dg(s), \\& F_{1}x(t)= T_{\alpha }(t) \bigl(x_{0}-p(x) \bigr), \\& F_{2}x(t)= \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s) \bigl(f\bigl(s,x(s)\bigr)+Bu(s) \bigr)\,dg(s). \end{aligned}$$

From condition (i) of (H7), we can define the control for arbitrary function $x(\cdot ) \in G(K;X)$ as follows:

$$ u_{x}(t) = \varLambda ^{-1} \biggl[x_{1}-p(x)- T_{\alpha }(b) \bigl(x_{0}-p(x)\bigr)- \int _{0}^{b}(b-s)^{\alpha -1}S_{\alpha }(b-s)f \bigl(s,x(s)\bigr)\,dg(s) \biggr](t). $$

Let $r \geq 0$ and $B_{r}=\{G(K;X):\|x\|_{\infty }< r\}$, we denote $\overline{B_{r}}=\{G(K;X):\|x\|_{\infty }\leq r\}$.

The proof process is divided into three steps.

Step I. Claim 1: we can find a positive number r such that $F(\overline{B_{r}})\subseteq \overline{B_{r}}$.

Claim 2: we show that, for any $x,\overline{x}\in B_{r}$, we can derive $F_{1}x+F_{2}\overline{x} \in B_{r}$.

In order to prove Claim 1, we can prove by contradiction. We suppose that there is a function $x_{r}(\cdot ) \in \overline{B_{r}}$ satisfying $\|F(x_{r})(t)\|>r$ for some $t \in K$. According to assumptions (H1)–(H4), we have

$$\begin{aligned}& \bigl\Vert F(x_{r}) (t) \bigr\Vert \\& \quad = \biggl\Vert T_{\alpha }(t) \bigl(x_{0}-p(x_{r}) \bigr) \\& \qquad {} + \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)f \bigl(s,x_{r}(s)\bigr)\,dg(s) \\& \qquad{} + \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)Bu(s) \,dg(s) \biggr\Vert \\& \quad \leq M_{1}\bigl( \Vert x_{0} \Vert + \bigl\Vert p(x_{r}) \bigr\Vert \bigr) \\& \qquad {} +\frac{M_{1}}{\varGamma (\alpha )} \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{0}^{b} \bigl\Vert f \bigl(s,x_{r}(s)\bigr) \bigr\Vert ^{p}\,dg(s) \biggr)^{\frac{1}{p}} \\& \qquad {} + \bigl\Vert S_{\alpha }(t-s)B \bigr\Vert \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{0}^{b} \bigl\Vert u(s) \bigr\Vert ^{p}\,dg(s) \biggr)^{\frac{1}{p}} \\& \quad \leq M_{1}\bigl( \Vert x_{0} \Vert + \bigl\Vert p(x_{r}) \bigr\Vert \bigr) \\& \qquad {} +\sup_{t\in [0,b]} \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \Vert h \Vert _{\mathit{HLS}_{g}^{p}} + \frac{M_{1}M_{2} \Vert u \Vert _{\mathit{HLS}}}{\varGamma (\alpha )} \biggr) \\& \quad \leq r, \end{aligned}$$

where

$$\begin{aligned}& \Vert u_{x_{r}} \Vert _{\mathit{HLS}} \\& \quad = \biggl\Vert \varLambda ^{-1} \biggl[x_{1}-p(x)-T_{ \alpha }(b) \bigl(x_{0}-p(x)\bigr) \\& \qquad {} - \int _{0}^{b}(b-s)^{\alpha -1}S_{\alpha }(t-s)f \bigl(s,x(s)\bigr)\,dg(s) \biggr] \biggr\Vert _{\mathit{HLS}} \\& \quad \leq M_{3} \biggl[ \Vert x_{1} \Vert +M_{1} \Vert x_{0} \Vert +(1+M_{1}) \bigl\Vert p(x) \bigr\Vert \\& \qquad {} + \biggl( \int _{0}^{b}\bigl[(b-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}}\frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \Vert h \Vert _{\mathit{HLS}_{g}^{p}} \biggr]. \end{aligned}$$

Due to $\|F(x_{r})(t)\|>r$, so we have

$$\begin{aligned}& \biggl(M_{1}+ \frac{M_{1}^{2}M_{2}M_{3}}{\varGamma (\alpha )} \biggr) \Vert x_{0} \Vert \\& \quad {} + \biggl(M_{1}+\frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha )}(1+M_{1}) \biggr) (cr+d)+ \biggl(M_{1}+\frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha )} \biggr) \Vert x_{1} \Vert \\& \quad {} +\frac{M_{1}}{\varGamma (\alpha )}\varPhi (r)\sup_{t\in [0,b]} \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl(1+ \frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha ) } \biggr) \Vert h \Vert _{\mathit{HLS}_{g}^{p}}>r. \end{aligned}$$

We divide the above inequality on both sides by r, then passing to the lower limit as $r \rightarrow + \infty$, we have

$$\begin{aligned}& c \biggl(M_{1}+\frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha )}(1+M_{1}) \biggr) \\& \quad {} +\frac{M_{1}\gamma }{\varGamma (\alpha )}\sup_{t\in [0,b]} \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl(1+ \frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha ) } \biggr) \Vert h \Vert _{\mathit{HLS}_{g}^{p}} \geq 1. \end{aligned}$$

It is a contradiction to (4.1). So we can find some positive number r satisfying $F(\overline{B_{r}})\subseteq \overline{B_{r}}$.

Based on Claim 1, it is easy to prove Claim 2 as follows:

For $t \in K$ and $x, \overline{x} \in \overline{B_{r}}$, we get that

$$\begin{aligned}& \bigl\Vert F_{1}(x) (t)+F_{2}(\overline{x}) (t) \bigr\Vert \\& \quad = \biggl\Vert T_{\alpha }(t) \bigl(x_{0}-p(x_{r}) \bigr) \\& \qquad {} + \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)f \bigl(s, \overline{x}(s)\bigr)\,dg(s) + \int _{0}^{t}(t-s)^{\alpha -1}S_{\alpha }(t-s)Bu(s) \,dg(s) \biggr\Vert \\& \quad \leq M_{1}\bigl( \Vert x_{0} \Vert + \bigl\Vert p(x_{r}) \bigr\Vert \bigr) \\& \qquad {} +\frac{M_{1}}{\varGamma (\alpha )} \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{0}^{b} \bigl\Vert f\bigl(s, \overline{x}(s)\bigr) \bigr\Vert ^{p}\,dg(s) \biggr)^{\frac{1}{p}} \\& \qquad{} + \bigl\Vert S_{\alpha }(t-s)B \bigr\Vert \biggl( \int _{0}^{t}\bigl[(t-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \int _{0}^{b} \bigl\Vert u(s) \bigr\Vert ^{p}\,dg(s) \biggr)^{\frac{1}{p}} \\& \quad \leq M_{1}\bigl( \Vert x_{0} \Vert + \bigl\Vert p(x_{r}) \bigr\Vert \bigr) \\& \qquad {} +\sup_{t\in [0,b]} \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl( \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \Vert h \Vert _{\mathit{HLS}_{g}^{p}} + \frac{M_{1}M_{2} \Vert u_{x_{r}} \Vert _{\mathit{HLS}}}{\varGamma (\alpha )} \biggr) \\& \quad \leq r, \end{aligned}$$

we can derive $F_{1}(x)(t)+F_{2}(\overline{x})(t) \in \overline{B_{r}}$.

Step II. $F_{1}$ is continuous on $\overline{B_{r}}$.

Let $\lim x^{n} \rightarrow x \in \overline{B_{r}}$ as $n\rightarrow \infty$, where $\{x^{n}\}^{\infty }_{n=1}$ is a sequence in $\overline{B_{r}}$. Then we have

$$ \bigl\Vert F_{1}\bigl(x^{n}\bigr) (t)-F_{1}(x) (t) \bigr\Vert \leq \bigl\Vert T_{\alpha }(t) \bigr\Vert \bigl\Vert p\bigl(x^{n}\bigr)-p(x) \bigr\Vert , $$

from the continuity of $p(x)$, we derive that the operator $F_{1}:\overline{B_{r}} \rightarrow \overline{B_{r}}$ is continuous.

Step III. The operator $F_{1}$ is compact.

Let $u,v \in K$, $0<\mu <\nu <b$, we have

$$\begin{aligned} \bigl\Vert F_{1}(x) (\nu )-F_{1}(x) (\mu ) \bigr\Vert \leq & \bigl\Vert T_{\alpha }( \nu )-T_{\alpha }(\mu ) \bigr\Vert \bigl( \Vert x_{0} \Vert + \bigl\Vert p(x) \bigr\Vert \bigr) \\ \leq & \bigl\Vert T_{\alpha }(\nu )-T_{\alpha }(\mu ) \bigr\Vert (r+cr+d), \end{aligned}$$

due to the strong continuity of $T_{\alpha }$, we can conclude that $\lim_{\mu \rightarrow \nu }\|T_{\alpha }(\nu )-T_{\alpha }(\mu )\|=0$, which implies that $F_{1}(\overline{B_{r}})$ is equicontinuous. According to Ascoli theorem, we get $F_{1}$ is a compact mapping.

Step IV. $F(\overline{B_{r}})$ is equiregulated on K.

For any $t_{0}\in [0,b)$, we get

$$\begin{aligned}& \bigl\Vert F(x) (t)-F(x) \bigl(t_{0}^{+}\bigr) \bigr\Vert \\& \quad \leq \bigl\Vert \bigl(T_{\alpha }(t)-T_{\alpha } \bigr) \bigl(t_{0}^{+}\bigr) \bigl(x_{0}-p(x)\bigr) \bigr\Vert \\& \qquad {}+ \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}S_{ \alpha }(t-s)-\bigl(t_{0}^{+}-s \bigr)^{\alpha -1}S_{\alpha }\bigl(t_{0}^{+}-s \bigr) \bigr)f\bigl(s,x(s)\bigr) \bigr\Vert \,dg(s) \\& \qquad {}+ \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}S_{ \alpha }(t-s)f \bigl(s,x(s)\bigr) \bigr\Vert \,dg(s) \\& \qquad {}+ \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}S_{ \alpha }(t-s)-\bigl(t_{0}^{+}-s \bigr)^{\alpha -1}S_{\alpha }\bigl(t_{0}^{+}-s \bigr) \bigr)Bu(s) \bigr\Vert \,dg(s) \\& \qquad {}+ \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}S_{\alpha }(t-s)Bu(s) \bigr\Vert \,dg(s) \\& \quad = A_{1}+A_{2}+A_{3}+A_{4}+A_{5}. \end{aligned}$$

In terms of the conditions we know that the set $\{p(x):x \in \overline{B_{r}}\}$ and $\{f(s,x(s)):s\in K,x \in \overline{B_{r}}\}$ are bounded. Furthermore, according to the compactness and strong continuity of $T(t)$, we know that $T(t)$ satisfies uniform operator topology continuity, and applying dominated convergence theorem, we can derive that $A_{1}$, $A_{2}$, $A_{4}$ all tend to zero independently of x as $t \rightarrow t_{0}^{+}$. Let $j(t)=\int _{0}^{t}k_{\alpha }(s)\,dg(s)$, where $k_{\alpha }(s)=(t-s)^{\alpha -1}h(s)$ referring to Proposition 2.3, $j(t):K \rightarrow X$ is a regulated function, we can obtain

$$\begin{aligned} A_{3} \leq & \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \int _{t_{0}^{+}}^{t} \bigl\Vert (t-s)^{\alpha -1}h(s) \bigr\Vert \,dg(s) \\ \leq & \frac{M_{1}}{\varGamma (\alpha )}\varPhi (r) \biggl( \bigl\Vert j(t)-j \bigl(t_{0}^{+}\bigr) \bigr\Vert + \int _{0}^{t_{0}^{+}} \bigl\Vert \bigl((t-s)^{\alpha -1}-\bigl(t_{0}^{+}-s \bigr)^{ \alpha -1} \bigr)h(s) \bigr\Vert \,dg(s) \biggr), \end{aligned}$$

when $t \rightarrow t_{0}^{+}$, we have $A_{3}\rightarrow 0$. In a similar way, we know that $A_{5}\rightarrow 0$ as $t \rightarrow t_{0}^{+}$. According to the above discussion, we can also derive that $\|F(x)(t_{0}^{-})-F(x)(t) \rightarrow 0\|$ as $t \rightarrow t_{0}^{-}$ for every $t_{0} \in (0,b]$. So $F(\overline{B_{r}})$ is equiregulated on K.

Step V. $F_{2}$ is a contraction mapping.

Suppose $D=\{x_{n}\}^{\infty }_{n=1} \subset \overline{B_{r}}$. In terms of assumptions (H2)(iii) and (H4)(ii), we can obtain

$$\begin{aligned} \sigma \bigl\{ u_{x_{n}}(s) \bigr\} ^{\infty }_{n=1} \leq & J(s)\sigma \biggl( \biggl\{ \int _{0}^{t}(t-s)^{\alpha -1}S_{ \alpha }(t-s) f\bigl(s,x_{n}(s)\bigr)\,dg(s) \biggr\} ^{\infty }_{n=1} \biggr) \\ \leq & J(s)\frac{2M_{1}}{\varGamma (\alpha )} \int _{0}^{t}(t-s)^{ \alpha -1}W(s)\sigma \bigl(D(s)\bigr)\,dg(s) \end{aligned}$$

and

$$\begin{aligned}& \sigma \bigl((F_{2}D) (t)\bigr) \\& \quad = \sigma \bigl({(F_{2}x_{n}) (t)}^{\infty }_{n=1} \bigr) \\& \quad \leq \sigma \biggl( \biggl\{ \int _{0}^{t}(t-s)^{\alpha -1}S_{ \alpha }(t-s)f \bigl(s,x_{n}(s)\bigr)\,dg(s) \biggr\} ^{\infty }_{n=1} \biggr) \\& \qquad {} +\sigma \biggl( \biggl\{ \int _{0}^{t}(t-s)^{\alpha -1}S_{ \alpha }(t-s)Bu_{x_{n}}(s) \,dg(s) \biggr\} ^{\infty }_{n=1} \biggr) \\& \quad \leq \frac{2M_{1}}{\varGamma (\alpha )} \int _{0}^{t}(t-s)^{ \alpha -1}W(s)\sigma \bigl(D(s)\bigr)\,dg(s) \\& \qquad {} +\frac{2M_{1}M_{2}}{\varGamma (\alpha )} \int _{0}^{t}(t-s)^{ \alpha -1}\sigma \bigl\{ u_{x_{n}}(s) \bigr\} ^{\infty }_{n=1}\,dg(s) \\& \quad \leq \biggl(\frac{2M_{1}}{\varGamma (\alpha )}+ \frac{4M_{1}^{2}M_{2}}{\varGamma (\alpha )^{2}} \int _{0}^{t}(t-s)^{ \alpha -1}J(s)\,dg(s) \biggr) \int _{0}^{t}(t-s)^{\alpha -1}W(s)\sigma \bigl(D(s)\bigr)\,dg(s) \\& \quad \leq \biggl(\frac{2M_{1}}{\varGamma (\alpha )}+ \frac{4M_{1}^{2}M_{2}}{\varGamma (\alpha )^{2}}\sup _{t\in [0,b]} \int _{0}^{t}(t-s)^{ \alpha -1}J(s)\,dg(s) \biggr) \\& \qquad {} \times \sup_{t\in [0,b]} \int _{0}^{t}(t-s)^{\alpha -1}W(s)\,dg(s) \sigma (D) \\& \quad = \varXi \sigma (D). \end{aligned}$$

Hence we can derive that operator $F_{2}$ is condensed. According to Krasnoselskii’s fixed point theorem, we see that the operator F has a fixed point in $\overline{B_{r}}$.

Then

$$\begin{aligned} x(b) =& T_{\alpha }(b) \bigl(x_{0}-p(x)\bigr)+ \int _{0}^{b}(b-s)^{ \alpha -1}S_{\alpha }(b-s)Bu_{x}(s) \,ds \\ &{} + \int _{0}^{b}(b-s)^{\alpha -1}S_{\alpha }(b-s)f \bigl(s,x(s)\bigr)\,dg(s) \\ =& -p(x)+x_{1}. \end{aligned}$$

Hence, the fractional measure evolution system (1.1) is nonlocally controllable on the interval K. The proof is completed. □

():

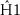The $C_{0}$-semigroup $T(t)$ generated by a linear operator $A:D(A)\subseteq X \rightarrow X$ is equicontinuous for $t>0$.

Theorem 4.3

Suppose that hypotheses (), (H2)–(H7) are satisfied, then the fractional measure evolution Eq. (1.1) is controllable on$(0,b]$if

$$ \begin{gathered}[b] c \biggl(M_{1}+\frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha )}(1+M_{1}) \biggr) \\ \quad {} +\frac{M_{1}\gamma }{\varGamma (\alpha )}\sup_{t\in [0,b]} \biggl( \int _{0}^{t}\bigl[(t-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl(1+ \frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha ) } \biggr) \Vert h \Vert _{\mathit{HLS}_{g}^{p}}< 1 \end{gathered} $$

(4.2)

and

$$ \biggl(\frac{4M_{1}^{2}M_{2}}{\varGamma (\alpha )^{2}}\sup_{t\in [0,b]} \int _{0}^{t}(t-s)^{\alpha -1}J(s)\,dg(s) + \frac{2M_{1}}{\varGamma (\alpha )} \biggr)\sup_{t\in [0,b]} \int _{0}^{t}(t-s)^{ \alpha -1}W(s)\,dg(s)< 1. $$

Proof

We can use the similar way in Theorem 4.2 to derive the result. □

5 An example

Consider the following fractional measure evolution equation:

$$ \textstyle\begin{cases} {}^{C} D_{0+}^{\alpha }x(t,z)=\frac{\partial ^{2}}{\partial z^{2}}x(t,z)\,dt+ (\frac{e^{-t}\sin x(t,z)}{e^{t}+e^{-t}}+\omega u(t,z) )\,dg(t),\\ \quad t\in [0, 1], z\in [0, \pi ], \\ x(0)+\frac{ \vert x \vert }{6+ \vert x \vert }=x_{0}. \end{cases} $$

(5.1)

Let

$$\begin{aligned}& A:D(A)\subseteq X \rightarrow X \quad \text{and}\quad Ay=y'', \\& \quad \text{where } D(A)=\bigl\{ y\in X:y, y' \text{ is absolutely continuous, }y'' \in X,y(0)=y(\pi )=0\bigr\} , \\& f:[0,1]\times X\rightarrow X \quad \text{and}\quad f\bigl(t,x(t,z)\bigr)= \frac{e^{-t}\sin x(t,z)}{e^{t}+e^{-t}}, \\& B:x\rightarrow X \quad \text{and}\quad Bu(t,z)=\mu u(t,z), \\& p:G\bigl([0,1];X\bigr)\rightarrow X \quad \text{and}\quad p\bigl(x(t,z) \bigr)= \frac{ \vert x(t,z) \vert }{6+ \vert x(t,z) \vert }. \end{aligned}$$

It is easy to see that A is the infinitesimal generator of an analytic semigroup $T(t)$ in X, taking $e_{n}(x)=\sqrt{2/\pi }\sin (nx)$ as an orthonormal basis in X,

$$ T(t)y=\sum^{\infty }_{n=1}e^{-n^{2}t} \langle y,e_{n} \rangle e_{n} , \quad t \geq 0 $$

and $\| T(t)\|\leq e^{-t}$, so there is $M_{1}>0$ satisfying $\| T(t)\|\leq M_{1}$.

$$\begin{aligned} \bigl\Vert f(t,x_{1})-f(t,x_{2}) \bigr\Vert =& \biggl( \int _{0}^{\pi } \biggl\vert \frac{e^{-t}\sin x_{1}}{e^{t}+e^{-t}}- \frac{e^{-t}\sin x_{2}}{e^{t}+e^{-t}} \biggr\vert ^{2}\,dz \biggr)^{\frac{1}{2}} \\ \leq & \biggl( \int _{0}^{\pi } \biggl\vert \frac{e^{-t}}{e^{t}+e^{-t}} \biggr\vert ^{2} \vert \sin x_{1}-\sin x_{2} \vert ^{2}\,dz \biggr)^{\frac{1}{2}} \\ \leq & \frac{1}{2} \biggl( \int _{0}^{\pi } \vert \sin x_{1}- \sin x_{2} \vert ^{2}\,dz \biggr)^{\frac{1}{2}} \\ \leq & \frac{1}{2} \biggl( \int _{0}^{\pi } \vert x_{1}-x_{2} \vert ^{2}\,dz \biggr)^{\frac{1}{2}} \\ \leq & \frac{1}{2} \Vert x_{1}-x_{2} \Vert . \end{aligned}$$

Moreover, we have

$$ \bigl\Vert f(t,x) \bigr\Vert = \biggl( \int _{0}^{\pi } \biggl\vert \frac{e^{-t}}{e^{t}+e^{-t}} \biggr\vert ^{2} \sin ^{2} x \,dz \biggr)^{\frac{1}{2}} \leq \frac{1}{2} \biggl( \int _{0}^{ \pi }\sin ^{2} x\,dz \biggr)^{\frac{1}{2}}\leq \frac{1}{2} \Vert x \Vert . $$

Taking $h(t)=\frac{1}{4}$, $\varPhi (\|x\|)=\|x\|$, we obtain that $h(t)$ and $\varPhi (t)$ satisfy assumption (H2).

$$\begin{aligned}& \begin{aligned} \bigl\Vert p\bigl(x_{1}(t,z)\bigr)-p \bigl(x_{2}(t,z)\bigr) \bigr\Vert &= \biggl( \int ^{\pi }_{0}\biggl( \frac{ \vert x_{1}(t,z) \vert }{6+ \vert x_{1}(t,z) \vert }- \frac{ \vert x_{2}(t,z) \vert }{6+ \vert x_{2}(t,z) \vert }\biggr)^{2}\,dz \biggr)^{\frac{1}{2}} \\ &\leq \frac{1}{6} \int ^{\pi }_{0} \vert x_{1}-x_{2} \vert ^{2}\,dz )^{\frac{1}{2}} \\ &\leq \frac{1}{6} \Vert x_{1}-x_{2} \Vert , \end{aligned}\\& \bigl\Vert p\bigl(x(t,z)\bigr) \bigr\Vert = \biggl( \int _{0}^{\pi } \biggl(\frac{ \vert x(t,z) \vert }{6+ \vert x(t,z) \vert } \biggr)^{2}\,dz \biggr)^{\frac{1}{2}} \leq \frac{1}{6} \Vert x \Vert \leq \frac{1}{6} \Vert x \Vert _{\infty }. \end{aligned}$$

We take $c=\frac{1}{6}$, $d=0$, hypothesis (H3) is satisfied.

We define the linear and bounded operator B and linear operator $\varLambda : \mathit{HLS}^{p}_{g}([0, 1]; X) \to X$ as follows:

$$ B(u)=\mu u(t,z),\quad z\in [0,\pi ] $$

and

$$ \varLambda u= \int ^{1}_{0}(1-s)^{\alpha -1}S_{\alpha }(1-s)Bu(s) \,dg(s). $$

It is easy to know that $\|B\|= \mu =M_{2}$, $\|\varLambda \|\leq \mu$. In terms of the inverse operator theorem, $\varLambda ^{-1}$ is the invertible operator of Λ and takes value in $\mathit{HLS}^{p}_{g}([0, 1];X)/\ker \varLambda$.

If the inequalities

$$\begin{aligned}& \frac{1}{6} \biggl(M_{1}+ \frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha )}(1+M_{1}) \biggr) \\& \quad {} +\frac{1}{4}\frac{M_{1}}{\varGamma (\alpha )} \biggl( \int _{0}^{1}\bigl[(1-s)^{ \alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \biggl(1+ \frac{M_{1}M_{2}M_{3}}{\varGamma (\alpha ) } \biggr)< 1 \end{aligned}$$

and

$$\begin{aligned}& \biggl(\frac{4M_{1}^{2}M_{2}}{\varGamma (\alpha )^{2}} \biggl( \int _{0}^{1}\bigl[(1-s)^{\alpha -1} \bigr]^{q}\,dg(s) \biggr)^{\frac{1}{q}} \bigl\Vert J(s) \bigr\Vert _{\mathit{HLS}^{p}_{g}} +\frac{2M_{1}}{\varGamma (\alpha )} \biggr) \\& \quad {} \times \int _{0}^{1}(1-s)^{\alpha -1}W(s)\,dg(s)< 1 \end{aligned}$$

hold, then the conditions in Theorem 4.2 are satisfied, our results can be applied to problem (5.1).

6 Conclusions

This paper is concerned with the existence and nonlocal controllability of mild solution for fractional evolution equation driven by measure with nonlocal conditions for the first time. We prove the regulated proposition of fractional equation firstly, then by constructing operator F, using the noncompact measure method and different fixed point theorems, we derive some sufficient conditions to guarantee the existence and nonlocal controllability of mild solutions. Finally, an illustrative example is given to show the practical usefulness of the analytical results. Furthermore, we will investigate the fractional measure evolution equations with Riemann–Liouville and Hilfer fractional derivatives in the next work.