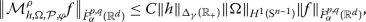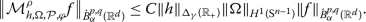- Research
- Open access
- Published:
A note on Marcinkiewicz integrals supported by submanifolds
Journal of Inequalities and Applications volume 2018, Article number: 228 (2018)
Abstract
In the present paper, we establish the boundedness and continuity of the parametric Marcinkiewicz integrals with rough kernels associated to polynomial mapping \(\mathcal{P}\) as well as the corresponding compound submanifolds, which is defined by
on the Triebel–Lizorkin spaces and Besov spaces when \(\Omega \in H ^{1}(\mathrm{S}^{n-1})\) and \(h\in \Delta_{\gamma }(\mathbb{R}_{+})\) for some \(\gamma >1\). Our main results represent significant improvements and natural extensions of what was known previously.
1 Introduction
As is well known, the Triebel–Lizorkin spaces and Besov spaces contain many important function spaces, such as Lebesgue spaces, Hardy spaces, Sobolev spaces and so on. During the last several years, a considerable amount of attention has been given to investigate the boundedness for several integral operators on the Triebel–Lizorkin spaces and Besov spaces. For examples, see [1–6] for singular integrals, [7–13] for Marcinkiewicz integrals, [14] for the Littlewood–Paley functions, [15–18] for maximal functions. In this paper we continue to focus on this topic. More precisely, we aim to establish the boundedness and continuity of parametric Marcinkiewicz integral operators associated to polynomial compound mappings with rough kernels in Hardy spaces \(H^{1}(\mathrm{S} ^{n-1})\) on the Triebel–Lizorkin spaces and Besov spaces.
We now recall the definitions of Triebel–Lizorkin spaces and Besov spaces.
Definition 1.1
Let \(d\geq 2\) and \(\mathcal{S}'( \mathbb{R}^{d})\) be the tempered distribution class on \(\mathbb{R} ^{d}\). For \(\alpha \in \mathbb{R}\) and \(0< p\), \(q\le \infty \) (\(p\neq\infty\)), the homogeneous Triebel–Lizorkin spaces \(\dot{F}_{\alpha }^{p,q}(\mathbb{R}^{d})\) and Besov spaces \(\dot{B}_{\alpha }^{p,q}( \mathbb{R}^{d})\) are defined by
where \(\widehat{\Psi _{i}}(\xi )=\phi (2^{i}\xi )\) for \(i\in \mathbb{Z}\) and \(\phi \in \mathcal{C}_{c}^{\infty } (\mathbb{R}^{d})\) satisfies the conditions: \(0\leq \phi (x)\leq 1\); \(\operatorname{supp}(\phi ) \subset \{x: 1/2\leq \vert x \vert \leq 2\}\); \(\phi (x)>c>0\) if \(3/5\leq \vert x \vert \leq 5/3\). The inhomogeneous versions of Triebel–Lizorkin spaces and Besov spaces, which are denoted by \(F_{\alpha }^{p,q} (\mathbb{R}^{d})\) and \(B_{\alpha }^{p,q}(\mathbb{R}^{d})\), respectively, are obtained by adding the term to the right hand side of (1.1) or (1.2) with \(\sum_{i\in \mathbb{Z}}\) replaced by \(\sum_{i\geq 1}\), where \(\Theta \in \mathcal{S}(\mathbb{R}^{d})\) (the Schwartz class), \(\operatorname{supp}(\hat{\Theta })\subset \{\xi : \vert \xi \vert \leq 2\}\), \(\hat{\Theta }(x)>c>0\) if \(\vert x \vert \leq 5/3\).
The following properties of the above spaces are well known (see [19–21] for more details):
Let \(n\geq 2\) and \(\mathrm{S}^{n-1}\) be the unit sphere in \(\mathbb{R} ^{n}\) equipped with the normalized Lebesgue measure dσ. Assume that \(\Omega \in L^{1}(\mathrm{S}^{n-1})\) is a function of homogeneous of degree zero and satisfies the cancelation condition
We denote by \(\Delta_{\gamma }(\mathbb{R}_{+})\) (\(\gamma \geq 1\)) the set of all measurable functions h defined on \(\mathbb{R}_{+}:=(0,\infty )\) satisfying
In 1986, Stein [22] first introduced the singular Radon transforms \(T_{h,\Omega ,\mathcal{P}}\) by
where \(\mathcal{P}=(P_{1},P_{2},\ldots ,P_{d})\) is a polynomial mapping from \(\mathbb{R}^{n}\) into \(\mathbb{R}^{d}\) and \(h\in \Delta_{1}( \mathbb{R}_{+})\). Later on, the bounds of \(T_{h,\Omega ,\mathcal{P}}\) on \(L^{p}\) spaces and other function spaces have been studied by a large number of scholars (see [4, 23, 24] for example). In particular, Chen et al. [4] established the bounds for \(T_{h, \Omega , \mathcal{P}}\) on Triebel–Lizorkin spaces and Besov spaces under the condition that \(\Omega \in H^{1} (\mathrm{S}^{n-1})\) and \(h\in \Delta_{\gamma }(\mathbb{R}_{+})\) for some \(\gamma >1\). It should be pointed out that the class of singular Radon transforms \(T_{h,\Omega ,\mathcal{P}}\) is closely related to the class of Marcinkiewicz integral operators
where h, Ω, \(\mathcal{P}\) are given as in (1.8) and \(\rho =\sigma +i\tau \) (\(\sigma ,\tau \in \mathbb{R}\) and \(\sigma >0\)). The operators defined in (1.9) have their roots in the classical Marcinkiewicz integral operator \(\mathcal{M}_{\Omega }\), which corresponds to the case \(\rho =1\), \(h(t)\equiv 1\), \(n=d\) and \(\mathcal{P}(y)=y\). In their fundamental work on the theory of Marcinkiewicz integrals, Stein [25] proved that \(\mathcal{M} _{\Omega }\) is of type \((p,p)\) for \(1< p\leq 2\) and of weak type \((1,1)\) if \(\Omega \in \operatorname{Lip}_{\alpha }(\mathrm{S}^{n-1})\) (\(0<\alpha\leq 1\)). Subsequently, the study of \(\mathcal{M}_{\Omega }\) and its extensions has attracted the attention of many authors. In 2002, Ding et al. [26] observed that \(\mathcal{M}_{h,\Omega , \mathcal{P}}^{\rho }\) with \(\rho =1\) is bounded on \(L^{p}(\mathbb{R} ^{d})\) for \(1< p<\infty \) if \(\Omega \in H^{1}(\mathrm{S}^{n-1})\) and \(h\in L^{\infty }(\mathbb{R}_{+})\). In 2009, Al-Qassem and Pan [27] proved that \(\mathcal{M}_{h,\Omega ,\mathcal{P}}^{\rho }\) is of type \((p,p)\) for \(\vert 1/p-1/2 \vert <\min \{1/2,1/\gamma '\}\) if \(\Omega \in L(\log^{+}L)^{1/2}(\mathrm{S}^{n-1})\) and \(h\in \Delta_{ \gamma }(\mathbb{R}_{+})\) for some \(\gamma >1\). It is well known that \(L(\log^{+}L)^{1/2}(\mathrm{S}^{n-1})\) and \(H^{1}(\mathrm{S}^{n-1})\) do not contain each other. We also note that \(L^{\infty }(\mathbb{R}_{+})= \Delta_{\infty } (\mathbb{R}_{+})\) and \(\Delta_{\gamma_{2}}( \mathbb{R}_{+}) \subsetneq \Delta_{\gamma_{1}}(\mathbb{R}_{+})\) for \(\gamma_{2}>\gamma_{1}>0\).
On the other hand, the investigation on the boundedness of Marcinkiewicz integral operators on Triebel–Lizorkin spaces and Besov spaces has attracted the attention of many authors. In 2009, Zhang and Chen [12] observed that \(\mathcal{M}_{h,\Omega }^{\rho }\) is bounded on \(F_{\alpha }^{p,q}(\mathbb{R}^{d})\) for \(0<\alpha <1\) and \(1< p\), \(q<\infty \) if \(\rho =1\), \(h\equiv 1\) and \(\Omega \in H^{1}( \mathrm{S}^{n-1})\). Subsequently, Zhang and Chen [13] further proved that \(\mathcal{M}_{h,\Omega }^{\rho }\) is bounded on \(F_{\alpha }^{p,q}(\mathbb{R}^{d})\) for \(0<\alpha <1\) and \(1+ \frac{n+1}{n+2-1/r}< p\), \(q<2+\frac{1-1/r}{n+1}\) if \(\rho =1\), \(h\in L^{\infty }(\mathbb{R}_{+})\) and \(\Omega \in L^{r}(\mathrm{S}^{n-1})\) with \(r>1\). Recently, Yabuta [10] improved and extended the above results to the case \(\Omega \in H^{1}(\mathrm{S}^{n-1})\) and \(h\in \Delta_{\gamma }(\mathbb{R}_{+})\) for some \(\gamma >1\). For other interesting work on this topic we refer the reader to [1, 7, 8, 28–33].
Based on the above, a natural question, which arises from the above results, is the following.
Question A
Is the operator \(\mathcal{M}_{h, \Omega , \mathcal{P}}^{\rho }\) bounded on Triebel–Lizorkin spaces and Besov spaces under the condition that \(\Omega \in H^{1}(\mathrm{S}^{n-1})\) and \(h\in \Delta_{\gamma }(\mathbb{R}_{+})\)?
Question A is the main motivation for this work. The main purpose of this paper will not only be to address the above question by treating a more general class of operators but also to establish the corresponding continuity of Marcinkiewicz integral operators on Triebel–Lizorkin spaces and Besov spaces. More precisely, let h, Ω, ρ, \(\mathcal{P}\) be given as in (1.9) and \(\varphi :\mathbb{R}_{+}\rightarrow \mathbb{R}\) be a suitable function, we define the parametric Marcinkiewicz integral operator \(\mathcal{M} _{h,\Omega , \mathcal{P},\varphi }^{\rho }\) on \(\mathbb{R}^{d}\) by
Our main result can be listed as follows.
Theorem 1.1
Let \(\mathcal{P}= (P_{1},P_{2}, \ldots ,P_{d})\) be a polynomial mapping from \(\mathbb{R}^{n}\) into \(\mathbb{R}^{d}\) and \(\varphi \in \mathfrak{F}\), where \(\mathfrak{F}\) is the set of all functions ϕ satisfying the following conditions:
-
(a)
ϕ is a positive increasing \(\mathcal{C}^{1} ( \mathbb{R}_{+})\) function;
-
(b)
there exist \(C_{\phi }\), \(c_{\phi }>0\) such that \(t\phi '(t) \geq C_{\phi }\phi (t)\) and \(\phi (2t)\leq c_{\phi }\phi (t)\) for all \(t>0\).
Suppose that \(\Omega \in H^{1}({\rm S}^{n-1})\) satisfies (1.7) and \(h\in \Delta_{\gamma }(\mathbb{R}_{+})\) for some \(\gamma >1\). Let \(\delta_{\gamma }=\max \{2, \gamma '\}\). Then
-
(i)
for \(\alpha \in (0,1)\) and \((1/p,1/q)\in \mathcal{R}_{ \gamma }\cup \{(1/p,1/p):\vert {1}/{p}-{1}/{2} \vert <1/\delta_{\gamma }\}\), there exists a constant \(C>0\) such that
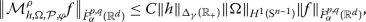
where \(\mathcal{R}_{\gamma }\) is the set of all interiors of the convex hull of three squares \(({1}/{2},{1}/{2}+ {1}/\delta_{\gamma })^{2}\), \(({1}/{2}-{1}/\delta_{\gamma }, {1}/{2})^{2}\) and \(({1}/{(2\gamma )},1- {1}/{(2\gamma )})^{2}\). Moreover, the operator \(\mathcal{M}_{h,\Omega ,\mathcal{P}, \varphi }^{\rho }\) is continuous from \(F_{\alpha }^{p,q} (\mathbb{R}^{d})\) to \(\dot{F}_{\alpha }^{p,q}(\mathbb{R}^{d})\).
-
(ii)
for \(\alpha \in (0,1)\), \(\vert {1}/{p}-{1}/{2} \vert <1/\delta_{ \gamma }\) and \(q\in (1,\infty )\), there exists a constant \(C>0\) such that
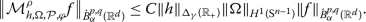
Moreover, the operator \(\mathcal{M}_{h,\Omega ,\mathcal{P}, \varphi } ^{\rho }\) is continuous from \(B_{\alpha }^{p,q} (\mathbb{R}^{d})\) to \(\dot{B}_{\alpha }^{p,q}(\mathbb{R}^{d})\).
The constants C may depend on α, ρ, p, q, n, d, φ and \(\deg (\mathcal{P})=\max_{1\leq i\leq d} \deg (P_{j})\), but they are independent of the coefficients of \(\{P_{j}\}\).
Remark 1.1
It was proved in [34] that the operator \(\mathcal{M}_{h,\Omega ,\mathcal{P}, \varphi }^{\rho }\) is of type \((p,p)\) for \(\vert {1}/{p}- {1}/{2} \vert <\min \{{1}/{2},{1}/{\gamma '} \}\) under the same conditions of Theorem 1.1. We observe that
for arbitrary functions f, g defined on \(\mathbb{R}^{d}\). Combining (1.11) with the \(L^{p}\) bounds for \(\mathcal{M}_{h, \Omega , \mathcal{P},\varphi }^{\rho }\) shows that \(\mathcal{M}_{h,\Omega , \mathcal{P},\varphi }^{\rho }\) is continuous on \(L^{p}(\mathbb{R}^{d})\) for \(\vert {1}/{p}-{1}/{2} \vert <\min \{{1}/{2},{1}/{\gamma '}\}\) under the same conditions of Theorem 1.1.
Remark 1.2
We remark that the set \(\mathcal{R} _{\gamma }\) was originally given by Yabuta [10] in the study of the boundedness for Marcinkiewicz integrals associated to surfaces \(\{\varphi (\vert y \vert )y':y\in \mathbb{R}^{n}\}\) with \(\varphi \in \mathfrak{F}\) on Triebel–Lizorkin spaces. Actually, Theorem 1.1 extends the partial result of [10, Theorem 1.1], which corresponds to the case \(n=d\), \(\rho >0\) and \(\mathcal{P}(y)=y\). Clearly, \(\mathcal{R} _{\gamma_{1}}\subsetneq \mathcal{R}_{\gamma_{2}}\) for any \(1<\gamma _{1}<\gamma_{2}\leq \infty \) and \(\mathcal{R}_{\infty }=(0,1)\times (0,1)\). There are some model examples for the class \(\mathfrak{F}\), such as \(t^{\alpha }\) (\(\alpha >0\)), \(t^{\beta }\ln (1+t)\) (\(\beta \geq 1\)), \(t\ln \ln (e+t)\), real-valued polynomials P on \(\mathbb{R}\) with positive coefficients and \(P(0)=0\) and so on. Note that there exists \(B_{\varphi }>1\) such that \(\varphi (2t) \geq B_{\varphi }\varphi (t)\) for any \(\varphi \in \mathfrak{F}\) (see [7]).
By the Properties (1.5) and (1.6), Remark 1.1 and Theorem 1.1, we can get the following result immediately.
Theorem 1.2
Under the same conditions of Theorem 1.1, the operator \(\mathcal{M}_{h,\Omega ,\mathcal{P}, \varphi }^{\rho }\) is bounded and continuous on \(F_{\alpha }^{p,q}( \mathbb{R}^{d})\) and \(B_{\alpha }^{p,q}(\mathbb{R}^{d})\), respectively.
Remark 1.3
Since \(L^{\infty }(\mathbb{R}_{+}) \subsetneq \Delta_{\gamma }(\mathbb{R}_{+})\) for any \(1<\gamma < \infty \) and \(L^{r}(\mathrm{S}^{n-1}) \subsetneq H^{1}(\mathrm{S}^{n-1})\) for any \(r>1\), the boundedness part in Theorem 1.2 improves and generalizes greatly the results of [12, 13]. It should be pointed out that our main results are new even in the special case: \(\rho =1\), \(n=d\), \(h(t)\equiv 1\) and \(\varphi (t)=t\).
The paper is organized as follows. Section 2 contains two vector-valued inequalities on maximal functions, which are the main ingredients of our proofs. Section 3 is devoted to presenting some preliminary lemmas. The proof of Theorem 1.2 will be given in Sect. 4. We would like to remark that some ideas in our proofs are taken from [7, 10, 17, 23, 34] and the main novelty in this paper is to give the continuity for Marcinkiewicz integral operators on Triebel–Lizorkin spaces and Besov spaces.
Throughout this note, we denote by \(p'\) the conjugate index of p, i.e. \({1}/{p}+{1}/{p'}=1\). The letter C or c, sometimes with certain parameters, will stand for positive constants not necessarily the same one at each occurrence, but are independent of the essential variables. If \(f\leq Cg\), we then write \(f\lesssim g\) or \(g\gtrsim f\); and if \(f\lesssim g\lesssim f\), we then write \(f\thicksim g\). In what follows, we denote by \(J^{-1}\) and \(J^{t}\) the inverse transform and the transpose of the linear transformation J, respectively. We also denote the Dirac delta function on \(\mathbb{R}^{d}\) by \(\delta_{\mathbb{R} ^{d}}\). For \(m\leq d\), we denote the projection operator from \(\mathbb{R}^{m}\) to \(\mathbb{R}^{d}\) by \(\pi_{m}^{d}\). We set \(\mathfrak{R}_{d}=\{\xi \in \mathbb{R}^{d}; 1/2<\vert \xi \vert \leq 1\}\). We also use the conventions \(\sum_{i\in \emptyset }a_{i}=0\) and \(\prod_{i\in \emptyset }a_{i}=1\).
Comments on conclusions and methods. This aim of this paper is to investigate the boundedness and continuity for the parametric Marcinkiewicz integral operators supported by polynomial compound mappings \(\mathcal{M}_{h, \Omega ,\mathcal{P},\varphi }^{ \rho }\) on the Triebel–Lizorkin spaces and Besov spaces. This is motivated by some recent results (see [4, 10, 11, 25, 31]). In [4], the authors established the bounds for the singular integral operators supported by polynomial mappings on the Triebel–Lizorkin spaces and Besov spaces; In [10, 11] the authors proved the boundedness for Marcinkiewicz integral operators \(\mathcal{M}_{h,\Omega }^{\rho }\) on the Triebel–Lizorkin spaces; In [25, 31] the authors gave the \(L^{p}\) bounds for the Marcinkiewicz integral operators supported by polynomial mappings \(\mathcal{M}_{h,\Omega ,\mathcal{P}}\). The main purpose of this paper will not only address the residual problems with respect to exponents [25, 31] but also establish the corresponding continuity of Marcinkiewicz integral operators on Triebel–Lizorkin spaces and Besov spaces. Although the methods and idea used in proofs of main results are motivated by some previous work [7, 10, 16, 22, 31], the methods and techniques are more delicate and difficult than those in the above references. Moreover, the main results are new and the proofs are highly non-trivial. On the other hand, the main results greatly extended and generalized some previous work [10–12].
2 Two vector-valued inequalities on maximal functions
The following lemma can be seen as a general case of [10, Lemma 6.1], which can be proved by [20, Theorem 4.6.1] and [20, Proposition 4.6.4]. We omit the details.
Lemma 2.1
Let \(\mathcal{B}_{1}\), \(\mathcal{B}_{2}\) be two Banach spaces and \(\rho (\cdot )\) denote the corresponding norm of \(\mathbb{R}^{d}\). Let T⃗ be a bounded linear operator from \(L^{p_{0}} (\mathcal{B}_{1},\mathbb{R}^{d})\) to \(L^{p_{0}}(\mathcal{B}_{2}, \mathbb{R}^{d})\) with norm \(A>0\) for some \(1< p_{0}\leq \infty \), for which there exists a kernel K⃗ defined on \(\mathbb{R}^{d}\backslash \{0\}\) that takes values in the space \(\mathcal{L}(\mathcal{B}_{1},\mathcal{B}_{2})\) such that
is well-defined as an element of \(\mathcal{B}_{2}\) for all \(L^{\infty }(\mathcal{B}_{1},\mathbb{R}^{d})\) functions F with compact supported provided x lies outside the support of F. Assume that the kernel K⃗ satisfies Hörmander condition
Then, for any \(1< p\), \(q<\infty \) and all \(\mathcal{B}_{1}\)-valued functions \(F_{j}\), there exists \(C>0\), such that
We now establish the following vector-valued inequality of a Hardy–Littlewood maximal function, which is of interest in its own right.
Lemma 2.2
Let \(\mathrm{M}_{(d)}\) be the Hardy–Littlewood maximal operator defined on \(\mathbb{R}^{d}\). Then
for all \(1< p,q,r,s<\infty \).
Proof
Let Φ be a positive radial symmetrically decreasing Schwartz function on \(\mathbb{R}^{d}\) such that \(\Phi (x) \geq 1\) when \(\vert x \vert \leq 1\). Let \(\Phi_{t}(x)=t^{-d}\Phi (\frac{x}{t})\) for all \(t>0\) and \(\mathrm{M}_{\Phi }^{d}(f)=\sup_{k\in \mathbb{Z}}\vert f*\Phi_{2^{k}} \vert \). As in [20, p. 336] we have
Let \(\mathcal{B}_{1}=L^{r}(\ell^{s},\mathfrak{R}_{d})\) and \(\mathcal{B}_{2}=L^{r}(\ell^{\infty }(\ell^{s}),\mathfrak{R}_{d})\) with \(1< r\), \(s<\infty \). Define the operator \(\overrightarrow{{\mathrm{M} _{\Phi }^{d}}}\) by
(2.1) together with the \(L^{r}(\ell^{s},\mathbb{R}^{d})\)-boundedness of the Hardy–Littlewood maximal functions and Fubini’s theorem shows that
which implies that \(\overrightarrow{\mathrm{M}_{\Phi }^{d}}\) is bounded from \(L^{r}(\mathcal{B}_{1},\mathbb{R}^{d})\) to \(L^{r}(\mathcal{B} _{2},\mathbb{R}^{d})\). On the other hand, for any \(x,y\in \mathbb{R}^{d}\),
From [20, (4.6.19)] we have
This together with (2.2) yields
Applying Lemma 2.1 with \(\rho (\cdot )=\vert \cdot \vert \), we obtain
for any \(1< p\), \(q<\infty \). This proves Lemma 2.2. □
We end this section by presenting the following lemma, which plays a key role in the proof of Theorem 1.1.
Lemma 2.3
([17])
Let \(\mathcal{P}=(P _{1},P_{2},\ldots ,P_{d})\) be a polynomial mapping from \(\mathbb{R} ^{n}\) into \(\mathbb{R}^{d}\) and \(\mathrm{M}_{\mathcal{P}}\) denote the Hardy–Littlewood maximal operator associated to \(\mathcal{P}\) defined by
Then, for any \(1< p,q,r<\infty \), there exists a constant \(C>0\) independent of the coefficients of \(\{P_{j}\}\) such that
3 Preliminary notations and lemmas
Let \(\mathcal{S}(\mathrm{S}^{n-1})\) be the Schwartz space of smooth functions on \(\mathrm{S}^{n-1}\) and \(\mathcal{S}'(\mathrm{S}^{n-1})\) denote its dual. For \(f\in \mathcal{S}'\), we define the radial maximal function \(P^{+}f\) by
The Hardy space \(H^{1}(\mathrm{S}^{n-1})\) is defined by
Let us recall the definition of atoms.
Definition 3.1
A function \(a(\cdot )\) on \(\mathrm{S}^{n-1}\) is a regular atom if there exist \(\varepsilon \in {\mathrm{S}}^{n-1}\) and \(\varrho \in (0,2]\) such that
The following lemma is the well-known atomic decomposition of Hardy space (see [35, 36]).
Lemma 3.1
For any \(\Omega \in H^{1}(\mathrm{S} ^{n-1})\) satisfying (1.1), there are complex numbers \(\{c_{j}\}\) and regular atoms \(\{\Omega_{j}\}\) such that \(\Omega =\sum_{j}c_{j}\Omega _{j}\) and .
Let h, Ω, ρ be given as in (1.3). For \(t>0\) and a mapping \(\Gamma :\mathbb{R}^{n} \rightarrow \mathbb{R}^{d}\), we define the measures \(\{\sigma_{h,\Omega ,\Gamma ,t,\rho }\}_{t>0}\) on \(\mathbb{R}^{d}\) by
We also define \(\sigma_{h,\Omega ,\Gamma ,\rho }^{*}\) on \(\mathbb{R} ^{d}\) by
where \(\vert \sigma_{h,\Omega ,\Gamma ,t,\rho } \vert \) is defined in the same way as \(\sigma_{h,\Omega ,\Gamma ,t,\rho }\), but with h and Ω replaced by \(\vert h \vert \) and \(\vert \Omega \vert \), respectively.
Lemma 3.2
Let \(\Gamma (y)= \mathcal{P}( \varphi (\vert y \vert )y')\) with \(\varphi \in \mathfrak{F}\) and \(\mathcal{P}=(P _{1},P_{2},\ldots ,P_{d})\) being a polynomial mapping from \(\mathbb{R}^{n}\) into \(\mathbb{R}^{d}\). Suppose that \(h\in \Delta_{ \gamma }(\mathbb{R}_{+})\) for some \(\gamma >1\) and \(\Omega \in L^{1}( \mathrm{S}^{n-1})\). Then, for \((1/p,1/q,1/r)\in \mathcal{Q}_{\gamma }\), there exists a constant \(C>0\) independent of the coefficients of \(\{P_{j}\}\) such that
holds for functions \(\{g_{j,\zeta ,k}\}_{j,\zeta ,k}\in L^{p} (\ell ^{q}(L^{r}(\ell^{2})),\mathbb{R}^{d})\), where \(\mathcal{Q}_{\gamma }\) is the set of all interiors of the convex hull of three cubes \((\frac{1}{2},\frac{1}{2}+ \frac{1}{\max \{2,\gamma '\}})^{3}\), \((\frac{1}{2}-\frac{1}{\max \{2,\gamma '\}},\frac{1}{2})^{3}\), and \((\frac{1}{2\gamma },1-\frac{1}{2\gamma })^{3}\).
Proof
To prove (3.4), it suffices to show that there exists a constant \(C>0\) independent of the coefficients of \(\{P_{j}\}\) such that
holds for functions \(\{g_{j,\zeta ,k}\}_{j,\zeta ,k}\in L^{p}(\ell ^{q}(L^{r}(\ell^{2},\mathfrak{R}_{d})),\mathbb{R}^{d})\) with \((1/p,1/q,1/r)\in \mathcal{Q}_{\gamma }\). By the change of variables and Hölder’s inequality,
which together with Lemma 2.3 and Minkowski’s inequality shows that
for any \(\gamma '< p,q,r<\infty \). Here \(C>0\) is independent of h, Ω and the coefficients of \(\{P_{j}\}\).
We now prove (3.5) by considering the following three cases:
Case 1 \((1<\gamma \leq \infty )\). By the duality argument, Hölder’s inequality, Fubini’s theorem and (3.6), we have, for any \(1< p,q,r<\gamma \), there exist functions \(\{f_{j,\zeta }\}_{j, \zeta }\) with such that
where \(\widetilde{f_{j,\zeta }}(x)=f_{j,\zeta }(-x)\). On the other hand, it follows from (3.6) that
for any \(\gamma '< p,q,r<\infty \). Interpolating between (3.7) and (3.8) shows that (3.5) holds for \((1/p,1/q,1/r)\) belonging to the interior of the cube \((\frac{1}{2\gamma }, 1-\frac{1}{2\gamma })^{3}\).
Case 2 \((1<\gamma \leq 2)\). By Hölder’s inequality, we have
It follows that
Observe that . By (3.9) and (3.7) with γ, p, q, r replacing by \(\frac{\gamma }{2-\gamma }\), \(\frac{p}{2}\), \(\frac{q}{2}\), \(\frac{r}{2}\), respectively we have (3.5) for \((1/p,1/q,1/r)\) belonging to the interior of the cube \((\frac{1}{2}- \frac{1}{\gamma '},\frac{1}{2})^{3}\). By duality, (3.5) also holds for \((1/p,1/q,1/r)\) belonging to the interior of the cube \((\frac{1}{2},\frac{1}{2}+\frac{1}{\gamma '})^{3}\). Interpolating these two cases, we see that (3.5) holds for \((1/p,1/q,1/r)\) belonging to the interior of the convex hull of two cubes \((\frac{1}{2}-\frac{1}{ \gamma '},\frac{1}{2})^{3}\) and \((\frac{1}{2},\frac{1}{2}+\frac{1}{ \gamma '})^{3}\). We notice that the interior of the cubes \((\frac{1}{2 \gamma }, 1-\frac{1}{2\gamma })^{3}\) contains in the interior of the convex hull of two cubes \((\frac{1}{2}-\frac{1}{\gamma '}, \frac{1}{2})^{3}\) and \((\frac{1}{2},\frac{1}{2}+ \frac{1}{\gamma '})^{3}\) when \(1<\gamma \leq 2\).
Case 3 \((\gamma \geq 2)\). Clearly, for \(\gamma \geq 2\). Interpolating between cases 1 and 2 we obtain (3.5) for \((1/p,1/q,1/r)\) belonging to the interior of the convex hull of three cubes \((\frac{1}{2\gamma },1-\frac{1}{2\gamma })^{3}\), \((0, \frac{1}{2})^{3}\) and \((\frac{1}{2},1)^{3}\). This completes the proof of Lemma 3.2. □
Let \(\{b_{k}\}\) be a lacunary sequence such that \(1<\delta_{1}\leq \frac{b _{k+1}}{b_{k}}\leq \delta_{2}\) for all \(k\in \mathbb{Z}\). Let \(\{\lambda_{k}\}_{k\in \mathbb{Z}}\) be a collection of \(\mathcal{C} _{0}^{\infty }(\mathbb{R}_{+})\) with the following properties: \(\operatorname{supp}(\lambda_{k}) \subset [b_{k}^{-1},b_{k-2}^{-1}]\), \(0\leq \lambda_{k}(t)\leq 1\) and \(\sum_{k\in \mathbb{Z}}\lambda_{k}(t)=1\). We have the following result.
Lemma 3.3
For \(m\leq d\), let \(H:\mathbb{R} ^{m}\rightarrow \mathbb{R}^{m}\) and \(H:\mathbb{R}^{d} \rightarrow \mathbb{R}^{d}\) be two nonsingular linear transformations. Define the multiplier operator \(S_{k}\) on \(\mathbb{R}^{d}\) by
Then, for \(1< p,q,r<\infty \), there exists a constant \(C>0\) depending only on \(\delta_{2}\) and d such that
Proof
Define the operator \(\vec{T}f: =\{\Phi_{k}*f \}_{k\in \mathbb{Z}}\) with \(\widehat{\Phi _{k}} (\xi )=\lambda_{k}(\vert \xi \vert )\). We first prove that
for any \(1< p,q,r<\infty \). One can easily check that \(\sum_{k\in \mathbb{Z}}\vert \widehat{\Phi _{k}}(\xi ) \vert ^{2}\leq 1\) for all \(\xi \neq 0\). By Plancherel’s theorem we see that T⃗ is bounded from \(L^{2}(\mathbb{R}^{d})\) to \(L^{2}(\ell^{2},\mathbb{R}^{d})\). Next we shall prove that
It is clear that
Taking \(\vert \alpha \vert =d+1\), we obtain
This together with the fact \(\vert x \vert ^{d+1}\leq C_{d} \sum_{\vert \beta \vert =d+1}\vert x^{\beta } \vert \) implies
On the other hand, we have, for any multi-index α and any \(j=1,2,\ldots ,d\),
Consequently,
From this inequality and the definition of \(\lambda_{k}\), we have
It follows that
Consequently,
By (3.12) and the fact that \(\vert x-y \vert \geq {\vert x \vert }/{2}\) for any \(\vert x \vert \geq 2\vert y \vert \),
Since \(\vert x-\theta y \vert \geq {\vert x \vert }/{2}\) for any \(\vert x \vert \geq 2\vert y \vert \) and \(\theta \in [0,1]\), we see from (3.13), for any \(\vert x \vert \geq 2\vert y \vert \), that there exists \(\theta \in [0,1]\) such that
This shows that
Equation (3.15) together with (3.14) yields (3.11). Invoking [20, Theorem 4.6.1] we see that T⃗ is bounded from \(L^{r}(\mathbb{R}^{d})\) to \(L^{r}(\ell^{2}, \mathbb{R}^{d})\) for any \(1< r<\infty \). For any \(1< r<\infty \), let \(\mathcal{B}_{1}=L^{r}( \mathfrak{R}_{d})\) and \(\mathcal{B}_{2}=L^{r}(\ell^{2},\mathfrak{R} _{d})\). By Fubini’s theorem and the \(L^{r}(\mathbb{R}^{d})\rightarrow L^{r}(\ell^{2}, \mathbb{R}^{d})\) boundedness for T⃗,
Note that
which together with (3.11) implies
Applying (3.16)–(3.17) and Lemma 2.1 with \(\rho (\cdot ) =\vert \cdot \vert \), we get (3.10).
We now define J by \(J=G^{-1}(H^{-1}\otimes \delta_{ \mathbb{R}^{d-m}})\). Observe that J is a nonsingular linear transformation on \(\mathbb{R}^{d}\). Denote \(y=(y^{1}, y^{2})\), where \(y^{1}=(y_{1},y_{2},\ldots ,y_{m})\) and \(y^{2}=(y_{m+1}, y_{m+2}, \ldots ,y_{d})\). One can easily check that
where \(f^{J}(\xi )=\vert J \vert ^{-1}f((J^{t})^{-1}\xi)\). By the change of variables, (3.10) and (3.18),
This completes the proof of Lemma 3.3. □
To prove Theorem 1.1, we need the following characterizations of the Triebel–Lizorkin spaces and Besov spaces.
Lemma 3.4
([10])
Let \(0<\alpha < \infty \) and M be an integer such that \(M>\alpha \). Let \(\triangle_{\zeta }^{M}f\) be the Mth difference of f for an arbitrary function f defined on \(\mathbb{R}^{d}\).
-
(i)
If \(1< p<\infty \), \(1< q\leq \infty \) and \(1\leq r<\min \{p,q \}\), then
is an equivalent norm in \(\dot{F}_{\alpha }^{p,q}(\mathbb{R}^{n})\).
-
(ii)
If \(1\leq p<\infty \), \(1\leq q\leq \infty \) and \(1\leq r \leq p\), then
is an equivalent norm in \(\dot{B}_{\alpha }^{p,q}(\mathbb{R}^{d})\).
4 Proof of Theorem 1.1
Let h, Ω, \(\mathcal{R}_{\gamma }\) be given as in Theorem 1.1 and \(\triangle_{\zeta }\) be the difference of f, i.e., \(\triangle_{\zeta }f(x)= f(x+\zeta )-f(x)\). We split the proof of Theorem 1.1 in two parts.
Step 1. Proof of (ii) of Theorem 1.1 . Let \(\alpha \in (0,1)\), \(\vert {1}/{p}-{1}/{2} \vert <\min \{{1}/{2},{1}/{\gamma '} \}\) and \(q\in (1,\infty )\). Observe that
By (4.1), Fubini’s theorem, Remark 1.1 and (ii) of Lemma 3.4, we have
This proves the boundedness part of (ii) of Theorem 1.1. By (1.11), (4.1), Remark 1.1 and [17, Proposition 1], we can get the continuity part of (ii) of Theorem 1.1.
Step 2. Proof of (i) of Theorem 1.1 . By (ii) of Theorem 1.1 and (1.6), we have
for \((1/p,1/q)\in \{(1/p,1/p):\vert {1}/{p}-{1}/{2} \vert <\min \{{1}/{2},{1}/ {\gamma '}\}\}\). Moreover, \(\mathcal{M}_{h,\Omega ,\mathcal{P},\varphi }^{\rho }\) is continuous from \(F_{\alpha }^{p,q}(\mathbb{R}^{d})\) to \(\dot{F}_{\alpha }^{p,q}(\mathbb{R}^{d})\) for \((1/p, 1/q)\in \{(1/p,1/p):\vert {1}/{p}-{1}/{2} \vert <\min \{{1}/{2}, {1}/{\gamma '}\}\}\). Therefore, it suffices to prove (4.2) for \((1/p,1/q)\in \mathcal{R}_{\gamma }\) and \(\mathcal{M}_{h,\Omega ,\mathcal{P},\varphi }^{\rho }\) is continuous from \(F_{\alpha }^{p,q}(\mathbb{R}^{d})\) to \(\dot{F}_{\alpha }^{p,q}( \mathbb{R}^{d})\) for \((1/p,1/q) \in \mathcal{R}_{\gamma }\).
By Lemma 3.1, to prove (4.2) for \((1/p,1/q)\in \mathcal{R}_{\gamma }\), it suffices to show that
for \((1/p,1/q)\in \mathcal{R}_{\gamma }\) when Ω is a regular atom satisfying (3.1)–(3.3). Without loss of generality we may assume \(\varepsilon =(0,\ldots ,0,1) \in \mathbb{R}^{n}\). We also only consider the case \(0<\varrho <1/4\) and omit the easier case \(\varrho \geq 1/4\). Let \(M(m)\), \(\{\Lambda_{\eta }\}_{\eta =1}^{M(m)}\), \(\{\Gamma_{\eta } \}_{\eta =0}^{M(m)}\) and \(\{L_{\eta }\}_{\eta =1}^{M(m)}\) be given as in [23]. Let \(\sigma_{h,\Omega ,\Gamma ,t,\rho }\) be defined as in Sect. 3 and \(\sigma_{k,t}^{\eta }= \sigma_{h, \Omega ,\Gamma_{\eta }(\varphi ),2^{k}t,\rho }\) with \(\Gamma_{\eta }(\varphi )(x)=\Gamma_{\eta }(\varphi (\vert x \vert )x')\). For \(\eta \in \{1,\ldots ,M(m)\}\), let \(s(\eta )=\operatorname{rank} (L_{\eta })\). By [23, Lemma 6.1], there are two nonsingular linear transformations \(H_{\eta }:\mathbb{R}^{s(\eta )}\rightarrow \mathbb{R}^{s(\eta )}\) and \(G_{\eta }:\mathbb{R}^{d}\rightarrow \mathbb{R}^{d}\) such that
Let \(\phi \in \mathcal{C}_{0}^{\infty }(\mathbb{R})\) such that \(\phi \equiv 1\) for \(\vert t \vert \leq 1/2\) and \(\phi \equiv 0\) for \(\vert t \vert >1\) and \(\psi (t)=\phi (t^{2})\). Define the family of measures \(\{\tau_{k,t} ^{\eta }\}_{t>0}\) by
for \(k\in \mathbb{Z}, t\in \mathbb{R}^{+}, \xi \in \mathbb{R}^{d}\) and \(1\leq \eta \leq M(m)\), where \(\{\delta (\eta )\}_{\eta =1}^{M(m)}\) and \(\{l(\eta )\}_{\eta =1}^{M(m)}\) are given as in [23] and
As in [34, (3.3)] we have
for \(k\in \mathbb{Z}\), \(t\in \mathbb{R}_{+}\), \(\xi \in \mathbb{R}^{d}\) and \(1\leq \eta \leq M(m)\), where \(\{\gamma (\eta )\}_{\eta =1}^{M(m)}\) are given as in [23]. Let \(B_{\varphi }\) be given as in Remark 1.2 and set \(a_{k,\eta }=\varphi (2^{k})^{l(\eta )} \varrho^{\delta ( \eta )}\Lambda_{\eta }^{-1}\). We note that \(B_{\varphi }^{l(\eta )} \leq \frac{a_{k+1,\eta }}{a_{k,\eta }} \leq c_{\varphi }^{l(\eta )}\) for any \(k\in \mathbb{Z}\). This together with (4.6) shows that
for any \(k\in \mathbb{Z}\), \(\xi \in \mathbb{R}^{d}\) and \(1\leq \eta \leq M(m)\). By the argument similar to those used in deriving [34, (3.9)], we obtain
Equation (4.8) together with (4.1), (i) of Lemma 3.4 and Minkowski’s inequality implies
for \(0<\alpha <1\) and \(1< p\), \(q<\infty \). Thus, to prove (4.3), it suffices to show that
for any \(1\leq \eta \leq M(m)\), \(\alpha \in (0,1)\) and \((1/p,1/q) \in \mathcal{R}_{\gamma }\).
We now prove (4.10). Let \(\{\upsilon_{k,\eta }\}_{k\in \mathbb{Z}}\) be a collection of \(\mathcal{C}^{\infty }(\mathbb{R}_{+})\) with the following properties:
Define the sequence of multiplier operators \(\{\Upsilon_{k,\eta }\} _{k\in \mathbb{Z}}\) on \(\mathbb{R}^{d}\) by
By Minkowski’s inequality,
Define the mixed norm for measurable functions on \(\mathbb{R}^{d}\times \mathfrak{R}_{d} \times \mathbb{Z} \times \mathbb{Z}\times \mathbb{R}_{+}\) by
For any \(j\in \mathbb{Z}\), let
Then (4.11) reduces to the following:
Thus, to prove (4.10), it suffices to show that for any \(\alpha \in (0,1)\) and \((1/p,1/q)\in \mathcal{R}_{\gamma }\), there exists \(\delta >0\) such that
By (4.7), Hölder’s inequality, Minkowski’s inequality, Fubini’s theorem, Plancherel’s theorem and (ii) of Lemma 3.4,
Combining this inequality with (1.4) implies that
Thus, we shall prove
for any \(\alpha \in (0,1)\) and \((1/p,1/q)\in \mathcal{R}_{\gamma }\). Indeed, (4.13) follows easily from the interpolation between (4.14) and (4.15).
For \(1\leq \iota \leq M(m)\), let \(\Phi^{\iota }\) be a radial function in \(\mathcal{S}(\mathbb{R}^{s(\iota )})\). Define \(J_{\iota }\) and \(X_{\iota }\) by
where
and
One can easily check that
Inequation (4.16) together with Lemma 2.2 shows that
for any \(1\leq \iota \leq M(m)\) and \(1< p\), \(q, r<\infty \). For any \(1\leq \eta \leq M(m)\), we define \(X^{\eta }f= X_{\eta }\circ X_{ \eta +1}\circ \cdots \circ X_{M(m)}f\). Then (4.17) shows that
for any \(1\leq \iota \leq M(m)\) and \(1< p,q,r<\infty \). On the other hand, we get from (4.5) that
It follows that
Combining (4.18)–(4.20) with Lemma 3.2 shows that
for \(\{g_{l,\zeta ,k}\}\in L^{p}(\ell^{q}(L^{r}(\ell^{2}, \mathfrak{R}_{d})),\mathbb{R}^{d})\) with \((1/p,1/q,1/r)\) belonging to the interior of the convex hull of three cubes \((\frac{1}{2}, \frac{1}{2}+\frac{1}{\max \{2, \gamma '\}})^{3}\), \((\frac{1}{2}-\frac{1}{ \max \{2,\gamma '\}}, \frac{1}{2})^{3}\), and \((\frac{1}{2\gamma }, 1-\frac{1}{2 \gamma })^{3}\). Let \(\alpha \in (0,1)\) and \((1/p,1/q)\in \mathcal{R} _{\gamma }\). We can choose \(1< r<\min \{p,q\}\) such that \((1/p,1/q,1/r)\) belongs to the interior of the convex hull of three cubes \(( \frac{1}{2},\frac{1}{2}+ \frac{1}{\max \{2,\gamma '\}})^{3}\), \((\frac{1}{2} -\frac{1}{\max \{2,\gamma '\}},\frac{1}{2})^{3}\), and \((\frac{1}{2\gamma },1-\frac{1}{2\gamma })^{3}\). By (4.21) and Lemmas 3.3 and 3.4, we obtain
This yields (4.15) and completes the proof of the boundedness part of (i).
We now prove the continuity part of (i). By Lemma 3.1, Minkowski’s inequality and (4.9)–(4.10), we have
for \(\alpha \in (0,1)\) and \((1/p,1/q)\in \mathcal{R}_{\gamma }\). Let \(\alpha \in (0,1)\), \((1/p,1/q)\in \mathcal{R}_{\gamma }\) and \(f_{j}\rightarrow f\) in \(F_{\alpha }^{p,q}(\mathbb{R}^{d})\) as \(j\rightarrow \infty \). We want to show that \(\mathcal{M}_{h,\Omega , \mathcal{P},\varphi }^{\rho }f_{j} \rightarrow \mathcal{M}_{h,\Omega ,\mathcal{P}, \varphi }^{\rho }f\) in \(\dot{F}_{\alpha }^{p,q}( \mathbb{R}^{d})\) as \(j\rightarrow \infty \). We shall prove this claim by contradiction. Without loss of generality we may assume that there exists \(c>0\) such that
for every j.
By (1.5) we see that \(f_{j}\rightarrow f\) in \(\dot{F}_{\alpha }^{p,q}( \mathbb{R}^{d})\) and in \(L^{p}(\mathbb{R}^{d})\) as \(j\rightarrow \infty \). It follows from (1.11) that \(\mathcal{M}_{h,\Omega , \mathcal{P},\varphi }^{\rho }f_{j}\rightarrow \mathcal{M}_{h,\Omega , \mathcal{P},\varphi }^{\rho }f\) in \(L^{p}(\mathbb{R}^{d})\) as \(j\rightarrow \infty \). Then by extracting a subsequence we may assume that \(\vert \mathcal{M}_{h,\Omega ,\mathcal{P},\varphi }^{\rho } f_{j}(x)-\mathcal{M}_{h,\Omega ,\mathcal{P}, \varphi }^{\rho }f(x) \vert \rightarrow 0\) as \(j\rightarrow \infty \) for almost every \(x\in \mathbb{R}^{d}\). It follows that \(\triangle_{2^{-l}\zeta }(\mathcal{M}_{h,\Omega , \mathcal{P}, \varphi }^{\rho }f_{j}-\mathcal{M}_{h,\Omega , \mathcal{P}, \varphi }^{\rho }f)(x)\rightarrow 0\) as \(j\rightarrow \infty \) for every \((l,\zeta )\in \mathbb{Z}\times \mathfrak{R}_{d}\) and almost every \(x\in \mathbb{R}^{d}\). We get from (4.1) and (1.11) that
for \((x,l,\zeta )\in \mathbb{R}^{d}\times \mathbb{Z}\times \mathfrak{R}_{d}\). For convenience, we set
for \(\alpha \in \mathbb{R}\) and \((p,q)\in (1,\infty )^{2}\). It follows from (i) of Lemma 3.4 that for \(\alpha \in (0,1)\) and \((p,q)\in (1,\infty )^{2}\). By (4.22) we obtain
It follows that as \(j\rightarrow \infty \). One can extract a subsequence such that . Define a function \(G:\mathbb{R}^{d}\times \mathbb{Z}\times \mathfrak{R}_{d} \rightarrow \mathbb{R}\) by
One can easily check that and
Since , we have \(\int_{\mathfrak{R}_{d}}G(x,k, \zeta )\,d\zeta <\infty \) for every \(k\in \mathbb{Z}\) and almost every \(x\in \mathbb{R}^{d}\). Inequation (4.23) together with the dominated convergence theorem leads to
for every \(l\in \mathbb{Z}\) and almost every \(x\in \mathbb{R}^{d}\). By the fact again,
for almost every \(x\in \mathbb{R}^{d}\). Using (4.23) we obtain
for almost every \(x\in \mathbb{R}^{d}\) and \(l\in \mathbb{Z}\). It follows from (4.24)–(4.26) and the dominated convergence theorem that
for almost every \(x\in \mathbb{R}^{d}\). By (4.23) again, we have
for almost every \(x\in \mathbb{R}^{d}\). By (4.27)–(4.28), the fact and the dominated convergence theorem, we get
This leads to as \(j\rightarrow \infty \), which is a contradiction. □
References
Al-Qassem, H.M., Cheng, L.C., Pan, Y.: Boundedness of rough integral operators on Triebel–Lizorkin spaces. Publ. Mat. 56, 261–277 (2012)
Liu, F.: Rough singular integrals associated to surfaces of revolution on Triebel–Lizorkin spaces. Rocky Mt. J. Math. 47(5), 1617–1653 (2017)
Liu, F., Wu, H.: Singular integrals related to homogeneous mappings in Triebel–Lizorkin spaces. J. Math. Inequal. 11(4), 1075–1097 (2017)
Chen, Y., Ding, Y., Liu, H.: Rough singular integrals supported on submanifolds. J. Math. Anal. Appl. 368, 677–691 (2010)
Chen, J., Fan, D., Ying, Y.: Singular integral operators on function spaces. J. Math. Anal. Appl. 276(2), 691–708 (2002)
Chen, J., Zhang, C.: Boundedness of rough singular integral on the Triebel–Lizorkin spaces. J. Math. Anal. Appl. 337(2), 1048–1052 (2008)
Liu, F.: Integral operators of Marcinkiewicz type on Triebel–Lizorkin spaces. Math. Nachr. 290(1), 75–96 (2017)
Liu, F.: On the Triebel–Lizorkin space boundedness of Marcinkiewicz integrals along compound surfaces. Math. Inequal. Appl. 20(2), 515–535 (2017)
Liu, F.: A note on Marcinkiewicz integrals associated to surfaces of revolution. J. Aust. Math. Soc. 104, 380–402 (2018)
Yabuta, K.: Triebel–Lizorkin space boundedness of Marcinkiewicz integrals associated to surfaces. Appl. Math. J. Chin. Univ. Ser. B 30(4), 418–446 (2015)
Liu, F.: Boundedness and continuity of several integral operators with rough kernels in \(W\mathcal{F}_{\beta }(\mathrm{S}^{n-1})\) on Triebel–Lizorkin spaces. J. Funct. Spaces 2018, Article ID 6937510 (2018)
Zhang, C., Chen, J.: Boundedness of g-functions on Triebel–Lizorkin spaces. Taiwan. J. Math. 13(3), 973–981 (2009)
Zhang, C., Chen, J.: Boundedness of Marcinkiewicz integral on Triebel–Lizorkin spaces. Appl. Math. J. Chin. Univ. Ser. B 25(25), 48–54 (2010)
Liu, F.: A note of Littlewood–Paley functions on Triebel–Lizorkin spaces. Bull. Korean Math. Soc. 55(2), 659–672 (2018)
Korry, S.: Boundedness of Hardy–Littlewood maximal operator in the framework of Lizorkin–Triebel spaces. Rev. Mat. Complut. 15(2), 401–416 (2002)
Liu, F.: Rough maximal functions supported by subvarieties on Triebel–Lizorkin spaces. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 112(2), 593–614 (2018)
Liu, F., Wu, H.: On the regularity of maximal operators supported by submanifolds. J. Math. Anal. Appl. 453, 144–158 (2017)
Liu, F., Xue, Q., Yabuta, K.: Rough maximal singular integral and maximal operators supported by subvarieties on Triebel–Lizorkin spaces. Nonlinear Anal. 171, 41–72 (2018)
Frazier, M., Jawerth, B., Weiss, G.: Littlewood–Paley Theory and the Study of Function Spaces. CBMS Reg. Conf. Ser., vol. 79. Am. Math. Soc., Providence (1991)
Grafakos, L.: Classical and Modern Fourier Analysis. Prentice Hall, Upper Saddle River (2003)
Triebel, H.: Theory of Function Spaces. Monogr. Math., vol. 78. Birkhäuser, Basel (1983)
Stein, E.M.: Problems in harmonic analysis related to curvature and oscillatory integrals. In: Proceedings of the International Congress of Mathematicians (Berkeley, CA, 1986), vol. 1, 2, pp. 196–221. Am. Math. Soc., Providence (1987)
Fan, D., Pan, Y.: Singular integral operators with rough kernels supported by subvarieties. Am. J. Math. 119, 799–839 (1997)
Al-Salman, A., Pan, Y.: Singular integrals with rough kernels in \(L\log L(\mathrm{S}^{n-1})\). J. Lond. Math. Soc. 66(2), 153–174 (2002)
Stein, E.M.: On the function of Littlewood–Paley, Lusin and Marcinkiewicz. Trans. Am. Math. Soc. 88(2), 430–466 (1958)
Ding, Y., Fan, D., Pan, Y.: On the \(L^{p}\) boundedness of Marcinkiewicz integrals. Mich. Math. J. 50, 17–26 (2002)
Al-Qassem, H.M., Pan, Y.: On certain estimates for Marcinkiewicz integrals and extrapolation. Collect. Math. 60(2), 123–145 (2009)
Liu, F.: Continuity and approximate differentiability of multisublinear fractional maximal functions. Math. Inequal. Appl. 21(1), 25–40 (2018)
Liu, F., Wu, H.: \(L^{p}\)-bounds for Marcinkiewicz integrals associated to homogeneous mappings. Monatshefte Math. 181(4), 875–906 (2016)
Wang, J., Cheng, H., Li, Y., et al.: The geometrical analysis of a predator–prey model with multi-state dependent impulsive. J. Appl. Anal. Comput. 8(2), 427–442 (2018)
Wang, F., Chen, B., Lin, C., Zhang, J., Meng, X.: Adaptive neural network finite-time output feedback control of quantized nonlinear systems. IEEE Trans. Cybern. 48(6), 1839–1848 (2018)
Li, X., Zhao, Q.: A new integrable symplectic map by the binary nonlinearization to the super AKNS system. J. Geom. Phys. 121, 123–137 (2017)
Zhao, Q., Li, X.: A Bargmann system and the involutive solutions associated with a new 4-order lattice hierarchy. Anal. Math. Phys. 6(3), 237–254 (2016)
Liu, F., Wu, H.: On Marcinkiewicz integrals associated to compound mappings with rough kernels. Acta Math. Sin. Engl. Ser. 30(7), 1210–1230 (2014)
Coifman, R., Weiss, G.: Extension of Hardy spaces and their use in analysis. Bull. Am. Math. Soc. 83, 569–645 (1977)
Colzani, L.: Hardy spaces on spheres. Ph.D. thesis, Washington University, St. Louis (1982)
Acknowledgements
The author would like to express his deep gratitude to the referees for their carefully reading and invaluable comments.
Funding
This work was partially supported the NNSF of China (No. 11701333) and Support Program for Outstanding Young Scientific and Technological Top-notch Talents of College of Mathematics and Systems Science (No. Sxy2016K01).
Author information
Authors and Affiliations
Contributions
The author worked jointly in drafting and approving the final manuscript. The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, F. A note on Marcinkiewicz integrals supported by submanifolds. J Inequal Appl 2018, 228 (2018). https://doi.org/10.1186/s13660-018-1822-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-018-1822-8