- Research
- Open access
- Published:
Ergodicity of the implicit midpoint rule for nonexpansive mappings
Journal of Inequalities and Applications volume 2015, Article number: 4 (2015)
Abstract
We prove a mean ergodic theorem for the implicit midpoint rule for nonexpansivemappings in a Hilbert space. We obtain weak convergence for the general case andstrong convergence for certain special cases.
MSC: 47J25, 47N20, 34G20, 65J15.
1 Introduction
The first mean ergodic theorem for nonlinear noncompact operators was proved byBaillon [1]. Let C be a closed convex subset of a Hilbert space Hand let  be a nonexpansive mapping (i.e.,
be a nonexpansive mapping (i.e., for all
for all  ) with fixed points. Then, for each
) with fixed points. Then, for each , the Cesàro means
, the Cesàro means

converge weakly to a fixed point of T. This mean ergodic theorem wasextended by Bruck [2] to the setting of Banach spaces that are uniformly convex and have aFréchet differentiable norm. Baillon and Clement [3] also investigated ergodicity of the nonlinear Volterra integral equationsin Hilbert spaces.
It is quite natural to consider ergodic convergence of iterative algorithms in thecase where the sequences generated by the algorithms either are not guaranteed toconverge or not convergent at all. For instance, the double-backward method ofPassty [4] generates a sequence  in the recursive manner:
in the recursive manner:

where A and B are maximal monotone operators in a Hilbert spacesuch that  is also maximal monotone and the inclusion
is also maximal monotone and the inclusion is solvable, and
is solvable, and  and
and  are the resolvents of A and B,respectively, that is,
are the resolvents of A and B,respectively, that is,  and
and  . It is well known [5] that the sequence
. It is well known [5] that the sequence  generated by the double-backward method (1.1) failsto converge weakly, in general. However, Passty [4] showed that if the sequence of parameters,
generated by the double-backward method (1.1) failsto converge weakly, in general. However, Passty [4] showed that if the sequence of parameters,  , is in
, is in  , then the averages
, then the averages

converge weakly to a solution to the inclusion  .
.
The implicit midpoint rule (IMR) for nonexpansive mappings in a Hilbert spaceH, inspired by the IMR for ordinary differential equations [6–12], was introduced in [13]. This rule generates a sequence  via the semi-implicit procedure:
via the semi-implicit procedure:

where the initial guess  is arbitrarily chosen,
is arbitrarily chosen,  for all n, and
for all n, and  is a nonexpansive mapping with fixed points.
is a nonexpansive mapping with fixed points.
The IMR (1.3) is proved to converge weakly [13] in the Hilbert space setting provided the sequence satisfies the two conditions:
satisfies the two conditions:
(C1)  for all
for all 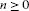 and some
and some  , and
, and
(C2)  .
.
However, this algorithm may fail to converge weakly without the assumption (C2). Wetherefore turn our attention to the ergodic convergence of the algorithm. We willshow that for any sequence  in the interval
in the interval  , the mean averages
, the mean averages 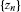 as defined by (1.2) will always converge weakly to afixed point of T as long as
as defined by (1.2) will always converge weakly to afixed point of T as long as  is an approximate fixed point of T(i.e.,
is an approximate fixed point of T(i.e.,  ). We will also show that under certain additionalconditions the means
). We will also show that under certain additionalconditions the means  can converge in norm to a fixed point of T.This paper is organized as follows. In the next section we introduce the concept ofnearest point projections and properties of nonexpansive mappings. The main resultsof this paper (i.e., weak and strong ergodicity of the IMR (1.3)) arepresented in Section 3.
can converge in norm to a fixed point of T.This paper is organized as follows. In the next section we introduce the concept ofnearest point projections and properties of nonexpansive mappings. The main resultsof this paper (i.e., weak and strong ergodicity of the IMR (1.3)) arepresented in Section 3.
2 Preliminaries
Let C be a nonempty closed convex subset of a Hilbert space H.Recall that the nearest point projection from H to C, , is defined by
, is defined by

We need the following characterization of projections.
Lemma 2.1LetCbe a nonempty closed convex subset of a Hilbert spaceH. Given and
and , then
, then if and only if any one of the following properties is satisfied:
if and only if any one of the following properties is satisfied:
-
(i)
 for all
for all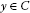 ;
; -
(ii)
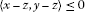 for all
for all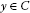 ;
; -
(iii)
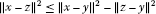 for all
for all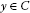 .
.
Recall that a mapping  is said to be nonexpansive if
is said to be nonexpansive if

A point  such that
such that  is said to be a fixed point of T. The set ofall fixed points of T is denoted by
is said to be a fixed point of T. The set ofall fixed points of T is denoted by  , namely,
, namely,

In the rest of this paper we always assume  .
.
We need the demiclosedness principle of nonexpansive mappings as described below.
Lemma 2.2[14]
LetCbe a closed convex subset of a Hilbert spaceHand let be a nonexpansive mapping. Then the mapping
be a nonexpansive mapping. Then the mapping is demiclosed in the sense that, for any sequence
is demiclosed in the sense that, for any sequence ofC, the following implication holds:
ofC, the following implication holds:

Next we need the following lemma (not hard to prove).
Lemma 2.3[15]
For each integer ,
,  such that
such that , points
, points , and any nonexpansive mapping
, and any nonexpansive mapping , we have
, we have

Recall also that the implicit midpoint rule (IMR) [13] generates a sequence  by the recursion process
by the recursion process

where  for all n, and
for all n, and  is a nonexpansive mapping.
is a nonexpansive mapping.
The following properties of the IMR (2.3) are proved in [13].
Lemma 2.4Let be any sequence in
be any sequence in and let
and let be the sequence generated by the IMR (2.3). Then
be the sequence generated by the IMR (2.3). Then
-
(i)
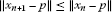 for all
for all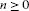 and
and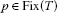 . In particular,
. In particular,  is bounded, and moreover, we have
is bounded, and moreover, we have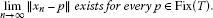 (2.4)
(2.4) -
(ii)
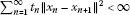 .
. -
(iii)
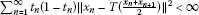 .
.
The convergence of the IMR (2.3) is proved in [13].
Theorem 2.5LetCbe a nonempty closed convex subset of a Hilbert spaceHand be a nonexpansive mapping with
be a nonexpansive mapping with . Assume
. Assume is generated by the IMR (2.3) where the sequence
is generated by the IMR (2.3) where the sequence of parameters satisfies the conditions (C1) and (C2) in theIntroduction. Then
of parameters satisfies the conditions (C1) and (C2) in theIntroduction. Then converges weakly to a fixed point ofT.
converges weakly to a fixed point ofT.
3 Ergodicity
In this section we discuss the ergodic convergence of the sequence generated by the IMR (2.3), that is, the convergenceof the means
generated by the IMR (2.3), that is, the convergenceof the means

where  is a sequence of positive numbers such that
is a sequence of positive numbers such that

Set  and let
and let  be the nearest point projection from H toF.
be the nearest point projection from H toF.
Lemma 3.1The sequence is convergent in norm.
is convergent in norm.
Proof First observe that

As a matter of fact, we get for  , by Lemma 2.1(i) and Lemma 2.4(i),
, by Lemma 2.1(i) and Lemma 2.4(i),

That is,  is decreasing and (3.3) is proven.
is decreasing and (3.3) is proven.
Applying the inequality (Lemma 2.1(iii))

to the case where  and
and  (with
(with  ) together with Lemma 2.4(i), we get
) together with Lemma 2.4(i), we get

The strong convergence of  follows immediately from the fact(3.3). □
follows immediately from the fact(3.3). □
Remark 3.2 The limit of  , which we denote by
, which we denote by  , can also be identified as the asymptotic center ofthe sequence
, can also be identified as the asymptotic center ofthe sequence  with respect to the fixed point set F ofT. In other words,
with respect to the fixed point set F ofT. In other words,

As a matter of fact, by (3.4) we get, for any  ,
,

Upon taking limsup we immediately obtain

Hence, (3.5) holds.
Theorem 3.3LetCbe a closed convex subset of a Hilbert spaceHand let be a nonexpansive mapping such that
be a nonexpansive mapping such that . Assume
. Assume is any sequence of positive numbers in the unit interval
is any sequence of positive numbers in the unit interval and let
and let be the sequence generated by the IMR (2.3). Define the means
be the sequence generated by the IMR (2.3). Define the means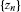 by (3.1), where the weights
by (3.1), where the weights are all positive and satisfy the condition (3.2). Assume, inaddition,
are all positive and satisfy the condition (3.2). Assume, inaddition,  . Then
. Then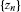 converges weakly to a pointz, where
converges weakly to a pointz, where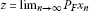 (in norm).
(in norm).
Proof Let 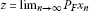 which is well defined by Lemma 3.1. ByLemma 2.1(ii), we have, for each k,
which is well defined by Lemma 3.1. ByLemma 2.1(ii), we have, for each k,

It turns out that, for  ,
,

(Here M is a constant such that  for all k.)
for all k.)
By multiplying by  and then summing up from
and then summing up from  to n, we conclude
to n, we conclude

We now claim that

Consequently, by Lemma 2.2, each weak cluster point of 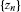 falls in F.
falls in F.
To see (3.7), we will prove that

for all n big enough, where  as
as  . For the sake of simplicity, we may, due to theassumption
. For the sake of simplicity, we may, due to theassumption  , assume that
, assume that

for all n.
Let  for
for  and let M be a constant such that
and let M be a constant such that . For each n, we put
. For each n, we put  for
for  and apply (2.2) to get
and apply (2.2) to get

Combining (3.9) and (3.10), we derive that

It turns out that (3.8) with  .
.
Now since  in norm, we see that the means
in norm, we see that the means in norm, as well. Consequently, if
in norm, as well. Consequently, if is a subsequence weakly converging to some point
is a subsequence weakly converging to some point , it follows from (3.6) that
, it follows from (3.6) that

This together with the fact that  implies that
implies that  . That is, z is the only weak cluster pointof the sequence
. That is, z is the only weak cluster pointof the sequence 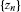 and therefore, we must have
and therefore, we must have  weakly. □
weakly. □
Remark 3.4 In Theorem 3.3 we assumed that  . This assumption is guaranteed if the sequence
. This assumption is guaranteed if the sequence satisfies the condition (C2) in the Introduction,that is,
satisfies the condition (C2) in the Introduction,that is,  . Indeed, by (C2) and Lemma 2.4(ii), we find
. Indeed, by (C2) and Lemma 2.4(ii), we find

Since the definition of IMR (2.3) yields

we also have

Combining (3.13) and (3.14), we infer that

Remark 3.5 If we assume (3.9) holds for all  , then we need some more delicate technicalitiesdealing with (3.10). We may proceed as follows. Decompose
, then we need some more delicate technicalitiesdealing with (3.10). We may proceed as follows. Decompose  (for
(for  ) as
) as

where

As  , we may assume
, we may assume  . Repeating the argument for (3.10) and (3.11), we get
. Repeating the argument for (3.10) and (3.11), we get

Let  . We finally obtain, for
. We finally obtain, for  ,
,

Next we show that in some circumstances, the sequence 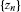 can converge strongly.
can converge strongly.
Theorem 3.6Let the assumptions of Theorem 3.3 holds. Then thesequence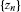 converges in norm to the point
converges in norm to the point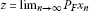 if, in addition, any one of the following conditions issatisfied:
if, in addition, any one of the following conditions issatisfied:
-
(i)
The fixed point setFofThas nonempty interior.
-
(ii)
Tis a contraction, that is,

where is a constant. In this case, the sequence
is a constant. In this case, the sequence generated by the IMR (2.3) converges in norm to the unique fixed pointofT.
generated by the IMR (2.3) converges in norm to the unique fixed pointofT.
-
(iii)
Tis compact, namely, Tmaps bounded sets to relatively norm-compact sets.
Proof (i) By assumption, we have  and
and  such that
such that
-
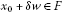 for all
for all 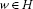 such that
such that 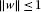 .
.
Therefore, upon substituting  for u in (3.6) we obtain
for u in (3.6) we obtain

for all 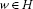 such that
such that 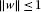 .
.
Taking the supremum in (3.15) over 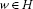 such that
such that 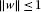 immediately yields
immediately yields

This verifies that  in norm.
in norm.
-
(ii)
Since T is a contraction, T has a unique fixed point which is denoted by p. By (2.3) we deduce that (noticing
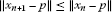 )
) 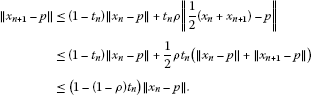
It turns out that

and hence

Since  , we must have
, we must have  . However, since the sequence
. However, since the sequence  is decreasing, we must have
is decreasing, we must have  . Namely,
. Namely,  in norm, and so
in norm, and so  in norm.
in norm.
-
(iii)
Since T is compact and since
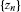 is weakly convergent,
is weakly convergent, 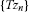 is relatively norm-compact. This together with (3.7) evidently implies that
is relatively norm-compact. This together with (3.7) evidently implies that 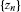 is relatively norm-compact. Therefore,
is relatively norm-compact. Therefore, 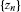 must converge in norm to
must converge in norm to 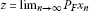 . □
. □
References
Baillon J-B: Un théorème de type ergodique pour les contractions nonlinéaires dans un espace de Hilbert.C. R. Acad. Sci. Paris Sér. A-B 1975,280(22):A1511-A1514. (in French)
Bruck RE: A simple proof of the mean ergodic theorem for nonlinear contractions inBanach spaces.Isr. J. Math. 1979,32(2–3):107–116. 10.1007/BF02764907
Baillon J-B, Clement P: Ergodic theorems for nonlinear Volterra equations in Hilbert space.Nonlinear Anal. 1981,5(7):789–801. 10.1016/0362-546X(81)90053-5
Passty GB: Ergodic convergence to a zero of the sum of monotone operators in Hilbertspaces.J. Math. Anal. Appl. 1979, 72:383–390. 10.1016/0022-247X(79)90234-8
Lions PL, Mercier B: Splitting algorithms for the sum of two nonlinear operators.SIAM J. Numer. Anal. 1979, 16:964–979. 10.1137/0716071
Auzinger W, Frank R: Asymptotic error expansions for stiff equations: an analysis for the implicitmidpoint and trapezoidal rules in the strongly stiff case.Numer. Math. 1989, 56:469–499. 10.1007/BF01396649
Bader G, Deuflhard P: A semi-implicit mid-point rule for stiff systems of ordinary differentialequations.Numer. Math. 1983, 41:373–398. 10.1007/BF01418331
Deuflhard P: Recent progress in extrapolation methods for ordinary differentialequations.SIAM Rev. 1985,27(4):505–535. 10.1137/1027140
Edith, E: Numerical and approximative methods in some mathematical models.Ph.D. thesis, Babes-Bolyai University of Cluj-Napoca (2006)
Schneider C: Analysis of the linearly implicit mid-point rule for differential-algebraequations.Electron. Trans. Numer. Anal. 1993, 1:1–10.
Somalia S: Implicit midpoint rule to the nonlinear degenerate boundary valueproblems.Int. J. Comput. Math. 2002,79(3):327–332. 10.1080/00207160211930
Somalia S, Davulcua S: Implicit midpoint rule and extrapolation to singularly perturbed boundaryvalue problems.Int. J. Comput. Math. 2000,75(1):117–127. 10.1080/00207160008804969
Alghamdi MA, Alghamdi MA, Shahzad N, Xu HK: The implicit midpoint rule for nonexpansive mappings.Fixed Point Theory Appl. 2014., 2014: Article ID 96
Goebel K, Kirk WA Cambridge Studies in Advanced Mathematics 28. In Topics in Metric Fixed Point Theory. Cambridge University Press, Cambridge; 1990.
Zarantonello EH: Projections on convex sets in Hilbert space and spectral theory. In Contributions to Nonlinear Functional Analysis. Edited by: Zarantonello EH. Academic Press, New York; 1971:237–424.
Acknowledgements
The authors are grateful to the anonymous referees for their helpful comments andsuggestions, which improved the presentation of this manuscript. This projectwas funded by the Deanship of Scientific Research (DSR), King AbdulazizUniversity, under grant No. (49-130-35-HiCi). The authors, therefore,acknowledge technical and financial support of KAU.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read andapproved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Xu, HK., Alghamdi, M.A. & Shahzad, N. Ergodicity of the implicit midpoint rule for nonexpansive mappings. J Inequal Appl 2015, 4 (2015). https://doi.org/10.1186/1029-242X-2015-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2015-4
 for all
for all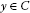 ;
;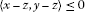 for all
for all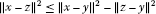 for all
for all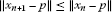 for all
for all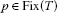 . In particular,
. In particular, 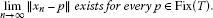
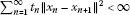 .
.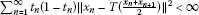 .
.
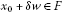 for all
for all 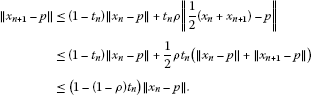
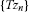 is relatively norm-compact. This together with (3.7) evidently implies that
is relatively norm-compact. This together with (3.7) evidently implies that