- Research
- Open access
- Published:
Symmetric duality for a higher-order nondifferentiable multiobjective programming problem
Journal of Inequalities and Applications volume 2015, Article number: 3 (2015)
Abstract
In this paper, a pair of Wolfe type higher-order nondifferentiable symmetric dual programs over arbitrary cones has been studied and then well-suited duality relations have been established considering K-F convexity assumptions. An example which satisfies the weak duality relation has also been depicted.
MSC:90C29, 90C30, 49N15.
1 Introduction
Consider the following multiobjective programming problem:

where  be open,
be open,  ,
,  , K, and C are closed convex pointed cones with nonempty interiors in
, K, and C are closed convex pointed cones with nonempty interiors in  and
and  , respectively.
, respectively.
Several researchers have studied the duality relations for different dual problems of (P) under various generalized convexity assumptions. Chen [1] considered a pair of symmetric higher-order Mond-Weir type nondifferentiable multiobjecive programming problems and established duality relations under higher-order F-convexity assumptions. Later on, Agarwal et al. [2] have filled some of the gap in the work of Chen [1] and proved a strong duality theorem for a Mond-Weir type multiobjective higher-order nondifferentiable symmetric dual program. Khurana [3] considered a pair of Mond-Weir type symmetric dual multiobjective programs over arbitrary cones and established duality results under cone-pseudoinvex and strongly cone-pseudoinvex assumptions. Later on, Kim and Kim [4] extended the results in Khurana [3] to the nondifferentiable multiobjective symmetric dual problem. Gupta and Jayswal [5] studied the higher-order Mond-Weir type multiobjective symmetric duality over cones using higher-order cone-preinvex and cone-pseudoinvex functions, which further extends some of the results in [3, 6, 7].
Agarwal et al. [8] formulated a pair of Mond-Weir type nondifferentiable multiobjective higher-order symmetric dual programs over arbitrary cones and established duality theorems under higher-order K-F convexity assumptions. In the recent work of Suneja and Louhan [9], the authors have considered Wolfe and Mond-Weir type differentiable symmetric higher-order dual pairs. The Mond-Weir type model studied in [9] is similar to the problem considered in Gupta and Jayswal [5]. However, the strong duality result in [9] is for arbitrary cones in  instead of only those cones which contain the nonnegative orthant of
instead of only those cones which contain the nonnegative orthant of  as considered in [5].
as considered in [5].
In the present paper, a pair of Wolfe type higher-order multiobjective nondifferentiable symmetric dual program have been formulated and we established weak, strong, and converse duality theorems under K-F convexity assumptions. We also illustrate a nontrivial example of a function which satisfies the weak duality relation.
2 Definitions and preliminaries
Let  and
and  be closed convex cones with nonempty interiors and let
be closed convex cones with nonempty interiors and let  and
and  be nonempty open sets in
be nonempty open sets in  and
and  , respectively such that
, respectively such that  . For a real valued twice differentiable function
. For a real valued twice differentiable function  defined on
defined on  ,
,  denotes the gradient vector of f with respect to x at
denotes the gradient vector of f with respect to x at  ,
,  denotes the Hessian matrix with respect to x at
denotes the Hessian matrix with respect to x at  . Similarly,
. Similarly,  ,
,  , and
, and  are also defined.
are also defined.
Definition 2.1 [8]
A point  is a weak efficient solution of (P) if there exists no
is a weak efficient solution of (P) if there exists no  such that
such that

Definition 2.2 [5]
A point  is an efficient solution of (P) if there exists no
is an efficient solution of (P) if there exists no  such that
such that

Definition 2.3 The positive dual cone  of K is defined by
of K is defined by

Definition 2.4 For all  , a functional
, a functional  is said to be sublinear with respect to the third variable, if
is said to be sublinear with respect to the third variable, if
-
(i)
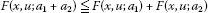 for all
for all  ,
, -
(ii)
 , for all
, for all 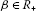 and for all
and for all 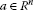 .
.
For convenience, we write  .
.
Definition 2.5 [8]
Let  be a sublinear functional with respect to the third variable. Also, let
be a sublinear functional with respect to the third variable. Also, let  ,
, 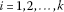 be a differentiable function. Then the function
be a differentiable function. Then the function  is said to be higher-order K-F convex in the first variable at
is said to be higher-order K-F convex in the first variable at  for fixed
for fixed  with respect to h, such that for
with respect to h, such that for  ,
,  ,
, 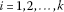 ,
,

Definition 2.6 [10]
Let φ be a compact convex set in  . The support function of φ is defined by
. The support function of φ is defined by

The subdifferentiable of  is given by
is given by

For any set  , the normal cone to S at a point
, the normal cone to S at a point  is defined by
is defined by

For each 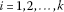 , let
, let  ,
,  and
and  be differentiable functions.
be differentiable functions.  and
and  , for
, for  and
and  ,
, 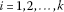 .
.  and
and  are the positive dual cones of
are the positive dual cones of  and
and  , respectively. D and E are the compact convex sets in
, respectively. D and E are the compact convex sets in  and
and  , respectively. Also, we use the following notations:
, respectively. Also, we use the following notations:

3 Problem formulation
Consider the following pair of Wolfe type higher-order nondifferentiable multiobjective symmetric dual programs:




where  is fixed.
is fixed.
Remark 3.1 If  and
and  , then our problems (WHP) and (WHD) become the problem studied in Suneja and Louhan [9].
, then our problems (WHP) and (WHD) become the problem studied in Suneja and Louhan [9].
Next, we will prove weak, strong, and converse duality results between (WHP) and (WHD).
Theorem 3.1 (Weak duality)
Let and
and be feasible solutions for (WHP) and (WHD), respectively. Assume the following conditions hold:
be feasible solutions for (WHP) and (WHD), respectively. Assume the following conditions hold:
-
(I)
 is higher-orderK-Fconvex atuwith respect to
is higher-orderK-Fconvex atuwith respect to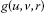 for fixedv,
for fixedv, -
(II)
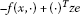 is higher-orderK-Gconvex atywith respect to
is higher-orderK-Gconvex atywith respect to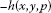 for fixed x,
for fixed x, -
(III)
 ,
,
where and
and are the sublinear functionals with respect to the third variable and satisfy the following conditions:
are the sublinear functionals with respect to the third variable and satisfy the following conditions:


Then

Proof We shall obtain the proof by contradiction. Let (5) not hold. Then

It follows from  and
and  that
that

Now, since  is higher-order K-F convex at u with respect to
is higher-order K-F convex at u with respect to 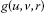 for fixed v, we get
for fixed v, we get

Using  and
and  , it follows that
, it follows that

Since  (by hypothesis (III)), hence
(by hypothesis (III)), hence  . Therefore, using (2) and sublinearity of F in the above expression, we obtain
. Therefore, using (2) and sublinearity of F in the above expression, we obtain

It follows from (A) and the dual constraint (3) that

for  .
.
Similarly, using hypothesis (II), (B),  , (1), (2), and sublinearity of G, we obtain
, (1), (2), and sublinearity of G, we obtain

for  .
.
Now, adding (7) and (8), we have

Finally, it follows from  and
and  that
that

which contradicts (6). Hence the result. □
Example 3.1 Let  ,
,  . Let
. Let  ,
,  , and
, and  .
.
Then  and
and  . Obviously,
. Obviously,  .
.
Let  ,
,  and
and  be defined as
be defined as

Let  and
and  . Then
. Then  and
and  . Suppose
. Suppose  . Also, suppose the sublinear functionals F and G are defined as
. Also, suppose the sublinear functionals F and G are defined as

Now, substituting the above defined expressions in the problems (WHP) and (WHD), we get

Now, we shall show that for the primal-dual pair (EP) and (ED), the hypotheses of Theorem 3.1 hold.
(A.1)  is higher-order K-F convex at
is higher-order K-F convex at  with respect to
with respect to 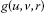 for fixed v and for all
for fixed v and for all  ,
,  , and we have
, and we have

(A.2) 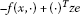 is higher-order K-G convex at
is higher-order K-G convex at  with respect to
with respect to 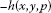 for fixed x and for all
for fixed x and for all  ,
,  , and we have
, and we have

(A.3)

The points  and
and  are feasible for the problems (EP) and (ED), respectively. These feasible points do satisfy the result of the weak duality theorem since
are feasible for the problems (EP) and (ED), respectively. These feasible points do satisfy the result of the weak duality theorem since

Theorem 3.2 (Strong duality)
Let be a weak efficient solution of (WHD). Let
be a weak efficient solution of (WHD). Let
-
(I)
the Hessian matrix
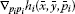 for all
for all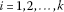 be positive or negative definite;
be positive or negative definite; -
(II)
 , for some
, for some imply that
imply that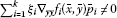 for all
for all ;
; -
(III)
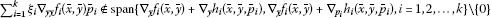 , for all
, for all ;
; -
(IV)
the set of vectors
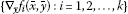 be linearly independent;
be linearly independent; -
(V)
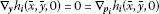 ,
,  ,
, 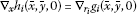 , for all
, for all .
.
Then
-
(I)
there exists
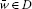 such that
such that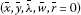 is feasible for (WHD) and
is feasible for (WHD) and -
(II)
the objective values of (WHP) and (WHD) are equal.
Also, if the hypotheses of Theorem 3.1 are satisfied for all feasible solutions of (WHP) and (WHD), then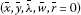 is an efficient solution for (WHD).
is an efficient solution for (WHD).
Proof Since  is a weak efficient solution for (WHP), by the Fritz John necessary optimality conditions [11], there exist
is a weak efficient solution for (WHP), by the Fritz John necessary optimality conditions [11], there exist  ,
,  , and
, and  such that
such that









Now, hypothesis (I) and (12) imply that

Using (18) in (10), we have

which yields

Now, we claim that  for all
for all 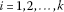 . On the contrary, suppose that for some
. On the contrary, suppose that for some  ,
,  , then using hypothesis (II), we have
, then using hypothesis (II), we have

This contradicts hypothesis (III) (by (20) and (21)). Hence,

Using (22) in (18), we have  ,
, 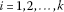 .
.
Since  ,
,  for at least one i,
for at least one i,

It follows from (11) and (23) that  ,
, 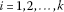 , which from
, which from  implies
implies  .
.
From (19), (22), and hypothesis (V), we get

which from hypothesis (IV) yields

Now, if  , then
, then  . Therefore, from (23), we get
. Therefore, from (23), we get  and hence,
and hence,  . This contradicts (17). Thus
. This contradicts (17). Thus  . Since
. Since  and
and  , we have
, we have

From (23) and (25), we obtain

Further, using inequalities (18), (23)-(25) in (9), we obtain

For  , it follows from (22) and hypothesis (V) that
, it follows from (22) and hypothesis (V) that

Let  . Then
. Then  and hence from (26), we have
and hence from (26), we have

Therefore,  .
.
Thus,  is a feasible solution for the dual problem.
is a feasible solution for the dual problem.
Consider  and
and  in (26), we get
in (26), we get

which implies that

Now, (15) and (23) yield  . Since
. Since  ,
,  .
.
Again as E is a compact convex set in  ,
,  .
.
Further, (13), (23), and (25) yield

By hypothesis (V) for  , (22), (27)-(28), we obtain
, (22), (27)-(28), we obtain

Hence, the two objective values are equal.
Now, let 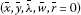 be not an efficient solution of (WHD), then there exists a point
be not an efficient solution of (WHD), then there exists a point  feasible for (WHD) such that
feasible for (WHD) such that

From (27), (28), and hypothesis (V) for  and
and  , we obtain
, we obtain

which contradicts Theorem 3.1. Hence,  is the efficient solution of (WHD). □
is the efficient solution of (WHD). □
Theorem 3.3 (Converse duality)
Let be a weak efficient solution of (WHP). Let
be a weak efficient solution of (WHP). Let
-
(I)
the Hessian matrix
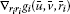 for all
for all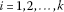 be positive or negative definite;
be positive or negative definite; -
(II)
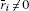 , for some
, for some implies that
implies that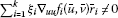 for all
for all ;
; -
(III)
 , for all
, for all ;
; -
(IV)
the set of vectors
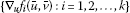 be linearly independent;
be linearly independent; -
(V)
 ,
,  ,
,  , for all
, for all .
.
Then
-
(I)
there exists
 such that
such that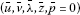 is feasible for (WHP) and
is feasible for (WHP) and -
(II)
the objective values of (WHP) and (WHD) are equal.
Also, if the hypotheses of Theorem 3.1 are satisfied for all feasible solutions of (WHP) and (WHD), then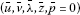 is an efficient solution for (WHP).
is an efficient solution for (WHP).
Proof The proof follows along the lines of Theorem 3.2. □
References
Chen X: Higher-order symmetric duality in nondifferentiable multiobjective programming problems.J. Math. Anal. Appl. 2004, 290:423–435. 10.1016/j.jmaa.2003.10.004
Agarwal RP, Ahmad I, Gupta SK: A note on higher-order nondifferentiable symmetric duality in multiobjective programming.Appl. Math. Lett. 2011, 24:1308–1311. 10.1016/j.aml.2011.02.021
Khurana S: Symmetric duality in multiobjective programming involving generalized cone-invex functions.Eur. J. Oper. Res. 2005, 165:592–597. 10.1016/j.ejor.2003.03.004
Kim MH, Kim DS: Nondifferentiable symmetric duality for multiobjective programming with cone constraints.Eur. J. Oper. Res. 2008, 188:652–661. 10.1016/j.ejor.2007.05.005
Gupta SK, Jayswal A: Multiobjective higher-order symmetric duality involving generalized cone-invex functions.Comput. Math. Appl. 2010, 60:3187–3192. 10.1016/j.camwa.2010.10.023
Gulati TR, Gupta SK: Higher-order symmetric duality with cone constraints.Appl. Math. Lett. 2009, 22:776–781. 10.1016/j.aml.2008.08.017
Gulati TR, Mehndiratta G: Nondifferentiable multiobjective Mond-Weir type second-order symmetric duality over cones.Optim. Lett. 2010, 4:293–309. 10.1007/s11590-009-0161-6
Agarwal RP, Ahmad I, Jayswal A: Higher-order symmetric duality in nondifferentiable multiobjective programming problems involving generalized cone convex functions.Math. Comput. Model. 2010, 52:1644–1650. 10.1016/j.mcm.2010.06.030
Suneja SK, Louhan P: Higher-order symmetric duality under cone-invexity and other related concepts.J. Comput. Appl. Math. 2014, 255:825–836.
Gupta SK, Kailey N, Kumar S:Duality for nondifferentiable multiobjective higher-order symmetric programs over cones involving generalized
 -convexity.J. Inequal. Appl. 2012., 2012: Article ID 298
-convexity.J. Inequal. Appl. 2012., 2012: Article ID 298Suneja SK, Aggarwal S, Davar S: Multiobjective symmetric duality involving cones.Eur. J. Oper. Res. 2002, 141:471–479. 10.1016/S0377-2217(01)00258-2
Acknowledgements
The authors wish to thank the reviewer for her/his valuable and constructive suggestions, which have considerably improved the presentation of the paper. The first author is also grateful to the Ministry of Human Resource and Development, India for financial support to carry out this work.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All the authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Debnath, I.P., Gupta, S.K. & Kumar, S. Symmetric duality for a higher-order nondifferentiable multiobjective programming problem. J Inequal Appl 2015, 3 (2015). https://doi.org/10.1186/1029-242X-2015-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2015-3
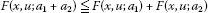 for all
for all  ,
, , for all
, for all 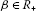 and for all
and for all 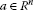 .
. ,
,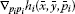 for all
for all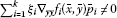 for all
for all ;
;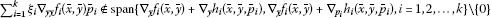 , for all
, for all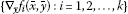 be linearly independent;
be linearly independent;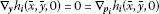 ,
,  ,
, 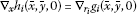 , for all
, for all .
.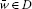 such that
such that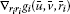 for all
for all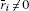 , for some
, for some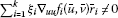 for all
for all , for all
, for all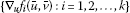 be linearly independent;
be linearly independent; ,
,  ,
,  , for all
, for all such that
such that -convexity.J. Inequal. Appl. 2012., 2012: Article ID 298
-convexity.J. Inequal. Appl. 2012., 2012: Article ID 298