- Research
- Open access
- Published:
Some results on a viscosity splitting algorithm in Hilbert spaces
Journal of Inequalities and Applications volume 2015, Article number: 2 (2015)
Abstract
In this paper, a viscosity splitting for common solution problems is proposed.Strong convergence theorems are obtained in the framework of Hilbert spaces.Applications are also provided to support the main results.
1 Introduction; preliminaries
In this paper, we always assume that H is a real Hilbert space with theinner product  and the induced norm
and the induced norm  for
for  . Recall that a set-valued mapping
. Recall that a set-valued mapping is said to be monotone iff, for all
is said to be monotone iff, for all ,
,  , and
, and  imply
imply  . In this paper, we use
. In this paper, we use  to denote the zero point set of M. Amonotone mapping
to denote the zero point set of M. Amonotone mapping  is maximal iff the graph
is maximal iff the graph of M is not properly contained in the graphof any other monotone mapping. It is well known that a monotone mapping Mis maximal if and only if, for any
of M is not properly contained in the graphof any other monotone mapping. It is well known that a monotone mapping Mis maximal if and only if, for any  ,
,  , for all
, for all  implies
implies  . For a maximal monotone operator M onH, and
. For a maximal monotone operator M onH, and  , we may define the single-valued resolvent
, we may define the single-valued resolvent , where
, where  denotes the domain of M. It is well knownthat
denotes the domain of M. It is well knownthat  is firmly nonexpansive, and
is firmly nonexpansive, and  .
.
The proximal point algorithm, which was proposed by Martinet [1, 2] and generalized by Rockafellar [3, 4] is one of the classical methods for solving zero points of maximalmonotone operators. In this paper, we investigate the problem of finding a zero ofthe sum of two monotone operators. The problem is very general in the sense that itincludes, as special cases, convexly constrained linear inverse problems, splitfeasibility problem, convexly constrained minimization problems, fixed pointproblems, variational inequalities, Nash equilibrium problem in noncooperative gamesand others. Because of their importance, splitting methods, which were proposed byLions and Mercier [5] and Passty [6], for zero problems have been studied extensively recently; see, forinstance, [7–17] and the references therein.
Let C be a nonempty closed and convex subset of H. Let be a mapping. Recall that the classical variationalinequality problem is to find a point
be a mapping. Recall that the classical variationalinequality problem is to find a point  such that
such that

Such a point  is called a solution of variational inequality (1.1).In this paper, we use
is called a solution of variational inequality (1.1).In this paper, we use  to denote the solution set of variational inequality(1.1). Recall that A is said to be monotone iff
to denote the solution set of variational inequality(1.1). Recall that A is said to be monotone iff

Recall that A is said to be inverse-strongly monotone iff thereexists a constant  such that
such that

For such a case, we also call A is κ-inverse-stronglymonotone. It is also not hard to see that every inverse-strongly monotone mapping ismonotone and continuous.
Let  be a mapping. In this paper, we use
be a mapping. In this paper, we use to denote the fixed point set of S.S is said to be contractive iff there exists a constant
to denote the fixed point set of S.S is said to be contractive iff there exists a constant such that
such that

We also call S is β-contractive. S is said to benonexpansive iff

It is well known if C is nonempty closed convex of H, then is not empty. S is said to be firmlynonexpansive iff
is not empty. S is said to be firmlynonexpansive iff

In order to prove our main results, we also need the following lemmas.
Lemma 1.1[18]
LetAbe a maximal monotone operator onH. For ,
,  , and
, and , we have
, we have , where
, where and
and .
.
Lemma 1.2[19]
Let and
and be bounded sequences inH. Let
be bounded sequences inH. Let be a sequence in
be a sequence in with
with . Suppose that
. Suppose that ,
,  and
and

Then .
.
Lemma 1.3[20]
Let be a sequence of nonnegative numbers satisfying the condition
be a sequence of nonnegative numbers satisfying the condition ,
,  , where
, where is a number sequence in
is a number sequence in such that
such that and
and ,
,  is a number sequence such that
is a number sequence such that . Then
. Then .
.
Lemma 1.4[21]
LetCbe a nonempty closed convex subset ofH. Let be a mapping and let
be a mapping and let be a maximal monotone operator. Then
be a maximal monotone operator. Then for all
for all .
.
Lemma 1.5[22]
Let be a real sequence that does not decreasing at infinity, in the sensethat there exists a subsequence
be a real sequence that does not decreasing at infinity, in the sensethat there exists a subsequence such that
such that for all
for all . For every
. For every , define an integer sequence
, define an integer sequence as
as . Then
. Then and for all
and for all
 .
.
Lemma 1.6[23]
LetCbe a nonempty closed convex subset ofH. Let be a nonexpansive mapping with a nonempty fixed point set. If
be a nonexpansive mapping with a nonempty fixed point set. If converges weakly toxand
converges weakly toxand converges to zero. Then
converges to zero. Then .
.
2 Main results
Now, we are in a position to state our main results.
Theorem 2.1LetCbe a nonempty closed convex subset ofH. Let be a nonexpansive mapping with fixed points and let
be a nonexpansive mapping with fixed points and let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let be anα-inverse-strongly monotone mapping and letBbe a maximal monotone operator onH. Assume that
be anα-inverse-strongly monotone mapping and letBbe a maximal monotone operator onH. Assume that and
and is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and let
and let be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
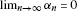 ,
, 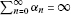 ;
; -
(b)
 ;
; -
(c)
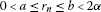 and
and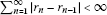 ,
,
whereaandbare two real numbers. Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Proof Note that the mapping  is nonexpansive. Indeed, we have
is nonexpansive. Indeed, we have

In light of restriction (c), one finds that  is nonexpansive. It is obvious that
is nonexpansive. It is obvious that . Fix
. Fix  . It follows that
. It follows that

Putting  , we see that
, we see that

By mathematical induction, we find that the sequence  is bounded. Note that
is bounded. Note that

Putting  , we find from Lemma 1.1 that
, we find from Lemma 1.1 that

This yields

It follows from restrictions (a) and (c) that

Using Lemma 1.2, we have  . It follows that
. It follows that

Since  , we find that
, we find that

Since  is convex, we find that
is convex, we find that

It follows that

Hence, we have

In view of restrictions (a), (b), and (c), we find from (2.1) that

Since  is firmly nonexpansive, we have
is firmly nonexpansive, we have

This implies from (2.3) that

On the other hand, we have

This implies that

In view of restrictions (a) and (b), we find from (2.1) and (2.4) that

Next, we show that  , where
, where  . To show it, we can choose a subsequence
. To show it, we can choose a subsequence of
of  such that
such that

Since  is bounded, we can choose a subsequence
is bounded, we can choose a subsequence of
of  which converges weakly some point x. We mayassume, without loss of generality, that
which converges weakly some point x. We mayassume, without loss of generality, that  converges weakly to x.
converges weakly to x.
Now, we are in a position to show that  . Set
. Set  . It follows that
. It follows that  . Since B is monotone, we get, for any
. Since B is monotone, we get, for any ,
,

Replacing n by  and letting
and letting  , we obtain from (2.5) that
, we obtain from (2.5) that

This gives  , that is,
, that is,  . This proves that
. This proves that  .
.
Now, we are in a position to prove that  . Notice that
. Notice that

This implies that  . This implies from (2.5) that
. This implies from (2.5) that  . Since
. Since  is demiclosed at zero, we find that
is demiclosed at zero, we find that . This complete the proof that
. This complete the proof that  . It follows that
. It follows that

Finally, we show that  . Notice that
. Notice that

This implies that

It follows that

In view of restrictions (a) and (b), we find from Lemma 1.3 that . This completes the proof. □
. This completes the proof. □
From Theorem 2.1, we have the following results immediately.
Corollary 2.2LetCbe a nonempty closed convex subset ofH. Let be a nonexpansive mapping with fixed points and let
be a nonexpansive mapping with fixed points and let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let and
and be real number sequences in
be real number sequences in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
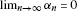 ,
, 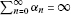 ;
; -
(b)
 .
.
Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Corollary 2.3LetCbe a nonempty closed convex subset ofH. Let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let be anα-inverse-strongly monotone mapping and letBbe a maximal monotone operator onH. Assume that
be anα-inverse-strongly monotone mapping and letBbe a maximal monotone operator onH. Assume that and
and is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and
and be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
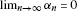 ,
, 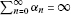 ;
; -
(b)
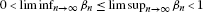 ;
; -
(c)
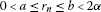 and
and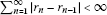 ,
,
whereaandbare two real numbers. Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Next, we give a result on the zeros of the sum of the operators A andB based on a different method.
Theorem 2.4LetCbe a nonempty closed convex subset ofH. Let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let be anα-inverse-strongly monotone mapping and letBbe a maximal monotone operator onH. Assume that
be anα-inverse-strongly monotone mapping and letBbe a maximal monotone operator onH. Assume that and
and is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and
and be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
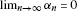 ,
, 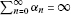 ;
; -
(b)
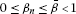 ;
; -
(c)
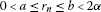 ,
,
where , a, andbare real numbers. Then
, a, andbare real numbers. Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Proof From the proof of Theorem 2.1, we find that is bounded. Since
is bounded. Since  is contractive, it has a unique fixed point. Next, weuse
is contractive, it has a unique fixed point. Next, weuse  to denote the unique fixed point. Note that
to denote the unique fixed point. Note that

It follows that

Since  is firmly nonexpansive and A isinverse-strongly monotone, we find that
is firmly nonexpansive and A isinverse-strongly monotone, we find that

Substituting (2.6) into (2.7), we find that

It follows that

Next, we consider the following possible two cases.
Case 1. Suppose that there exists some nonnegative integer m such that thesequence  is eventually decreasing. Then
is eventually decreasing. Then exists. By (2.8), we find that
exists. By (2.8), we find that

By use of restrictions (b) and (c), we have  . It also follows from (2.8) that
. It also follows from (2.8) that

From restrictions (b) and (c), we obtain

Hence, we have  . From Lemma 1.4, we find that
. From Lemma 1.4, we find that . This implies that
. This implies that  . Next, we show that
. Next, we show that  . To show it, we can choose a subsequence
. To show it, we can choose a subsequence of
of  such that
such that

Since  is bounded, we can choose a subsequence
is bounded, we can choose a subsequence of
of  which converges weakly to some point x. Wemay assume, without loss of generality, that
which converges weakly to some point x. Wemay assume, without loss of generality, that  converges weakly to x. Since the mapping
converges weakly to x. Since the mapping is nonexpansive, we find that
is nonexpansive, we find that  . It follows that
. It follows that  . In view of (2.8), we find from Lemma 1.3 that
. In view of (2.8), we find from Lemma 1.3 that .
.
Next, we consider another case.
Case 2. Suppose that the sequence  is not eventually decreasing. There exists asubsequence
is not eventually decreasing. There exists asubsequence  such that
such that  for all
for all  . We define an integer sequence
. We define an integer sequence as in Lemma 1.5. By use of (2.8), we have
as in Lemma 1.5. By use of (2.8), we have

It follows that

Hence, we have  . In view of (2.9), we find that
. In view of (2.9), we find that

Note that

By use of (2.10), we find that  . Since
. Since  , we find that
, we find that  . This completes the proof. □
. This completes the proof. □
Remark 2.5 Comparing Theorem 2.4 with the recent results announced in [7, 11] and [24], we have the following:
-
(i)
Our proofs are different from theirs.
-
(ii)
We remove the additional restriction
 .
.
3 Applications
In this section, we investigate solutions of equilibrium problems, variationalinequalities and convex minimization problems, respectively.
Let F be a bifunction of  into ℝ, where ℝ denotes the set of realnumbers. Recall the following equilibrium problem:
into ℝ, where ℝ denotes the set of realnumbers. Recall the following equilibrium problem:

In this paper, we use  to denote the solution set of the equilibriumproblem.
to denote the solution set of the equilibriumproblem.
To study equilibrium problems (3.1), we may assume that F satisfies thefollowing conditions:
(A1)  for all
for all  ;
;
(A2) F is monotone, i.e.,  for all
for all  ;
;
(A3) for each  ,
,

(A4) for each  ,
,  is convex and weakly lower semi-continuous.
is convex and weakly lower semi-continuous.
Lemma 3.1[24]
LetCbe a nonempty closed convex subset of a real Hilbert spaceH. LetFbe a bifunction from to ℝ which satisfies (A1)-(A4) and letBbe a multivalued mapping ofHinto itself defined by
to ℝ which satisfies (A1)-(A4) and letBbe a multivalued mapping ofHinto itself defined by

ThenBis a maximal monotone operator with the domain ,
,  , and
, and ,
,  ,
,  , where
, where is defined as
is defined as

Theorem 3.2LetCbe a nonempty closed convex subset ofH. Let be a nonexpansive mapping with fixed points and let
be a nonexpansive mapping with fixed points and let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let be anα-inverse-strongly monotone mapping and letFbe a bifunction from
be anα-inverse-strongly monotone mapping and letFbe a bifunction from to ℝ which satisfies (A1)-(A4). Assume that
to ℝ which satisfies (A1)-(A4). Assume that is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and let
and let be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

whereBis a mapping defined as in (3.2). Assume that the control sequencessatisfy the following restrictions:
-
(a)
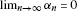 ,
, 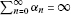 ;
; -
(b)
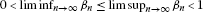 ;
; -
(c)
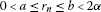 and
and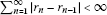 ,
,
whereaandbare two real numbers. Then converges strongly to a point
converges strongly to a point , which is a unique solution to the followingvariational inequality:
, which is a unique solution to the followingvariational inequality:

Theorem 3.3LetCbe a nonempty closed convex subset ofH. Let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let be anα-inverse-strongly monotone mapping and LetFbe a bifunction from
be anα-inverse-strongly monotone mapping and LetFbe a bifunction from to ℝ which satisfies (A1)-(A4). Assume that
to ℝ which satisfies (A1)-(A4). Assume that is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and let
and let be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
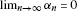 ,
, 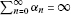 ;
; -
(b)
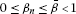 ;
; -
(c)
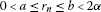 ,
,
where , a, andbare real numbers. Then
, a, andbare real numbers. Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Let  be a proper convex lower semi-continuous function.Then the subdifferential ∂g of g is defined as follows:
be a proper convex lower semi-continuous function.Then the subdifferential ∂g of g is defined as follows:

From Rockafellar [4], we know that ∂g is maximal monotone. It is easy to verifythat  if and only if
if and only if  . Let
. Let  be the indicator function of C,i.e.,
be the indicator function of C,i.e.,

Since  is a proper lower semi-continuous convex function onH, we see that the subdifferential
is a proper lower semi-continuous convex function onH, we see that the subdifferential  of
of  is a maximal monotone operator.
is a maximal monotone operator.
Lemma 3.4[24]
LetCbe a nonempty closed convex subset ofHand let be the metric projection fromHontoC. Let
be the metric projection fromHontoC. Let be the subdifferential of
be the subdifferential of , where
, where is as defined in (3.3). Then
is as defined in (3.3). Then ,
,  ,
,  ,
,
Theorem 3.5LetCbe a nonempty closed convex subset ofH. Let be a nonexpansive mapping with fixed points and let
be a nonexpansive mapping with fixed points and let be aβ-contractive mapping. Let
be aβ-contractive mapping. Let be anα-inverse-strongly monotone mapping. Assumethat
be anα-inverse-strongly monotone mapping. Assumethat is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and let
and let be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(1)
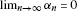 ,
, 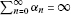 ;
; -
(2)
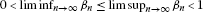 ;
; -
(3)
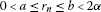 and
and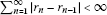 ,
,
whereaandbare two real numbers. Then converges strongly to a point
converges strongly to a point , which is a unique solution to the followingvariational inequality:
, which is a unique solution to the followingvariational inequality:

Proof Putting  , we find from Theorem 2.1 and Lemma 3.4 thedesired conclusion immediately. □
, we find from Theorem 2.1 and Lemma 3.4 thedesired conclusion immediately. □
Theorem 3.6LetCbe a nonempty closed convex subset ofH. Let be aβ-contractive mapping and let
be aβ-contractive mapping and let be anα-inverse-strongly monotone mapping. Assumethat
be anα-inverse-strongly monotone mapping. Assumethat is not empty. Let
is not empty. Let and
and be real number sequences in
be real number sequences in and let
and let be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
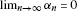 ,
, 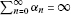 ;
; -
(b)
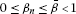 ;
; -
(c)
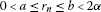 ,
,
where , a, andbare real numbers. Then
, a, andbare real numbers. Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Proof Putting  , we find from Theorem 2.4 and Lemma 3.4 thedesired conclusion immediately. □
, we find from Theorem 2.4 and Lemma 3.4 thedesired conclusion immediately. □
Let  be a convex and differentiable function and
be a convex and differentiable function and is a convex function. Consider the convexminimization problem
is a convex function. Consider the convexminimization problem  . From [25], we know if ∇W is
. From [25], we know if ∇W is  -Lipschitz continuous, then it isL-inverse-strongly monotone. Hence, we have the following results.
-Lipschitz continuous, then it isL-inverse-strongly monotone. Hence, we have the following results.
Theorem 3.7Let be a convex and differentiable function such that ∇Wis
be a convex and differentiable function such that ∇Wis -Lipschitz continuous and let
-Lipschitz continuous and let be a convex and lower semi-continuous function such that
be a convex and lower semi-continuous function such that is not empty. Letfbe aβ-contractive mapping onH. Let
is not empty. Letfbe aβ-contractive mapping onH. Let and
and be real number sequences in
be real number sequences in and let
and let be a positive real number sequence in
be a positive real number sequence in . Let
. Let be a sequence generated in the following process:
be a sequence generated in the following process:  and
and

Assume that the control sequences satisfy the following restrictions:
-
(a)
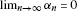 ,
, 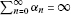 ;
; -
(b)
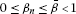 ;
; -
(c)
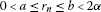 ,
,
where , a, andbare real numbers. Then
, a, andbare real numbers. Then converges strongly to a point
converges strongly to a point , which is also a unique solution to the followingvariational inequality:
, which is also a unique solution to the followingvariational inequality:

Proof Putting  and
and  , we find from Theorem 2.4 the desired conclusionimmediately. □
, we find from Theorem 2.4 the desired conclusionimmediately. □
4 Conclusions
In this paper, we study a convex feasibility problem via two monotone mappings and anonexpansive mapping. The common solution is also a unique solution of anothervariational inequality. The restrictions imposed on the sequence are mild. The results presented in this paper mainlyimprove the corresponding results in [7] and [11].
are mild. The results presented in this paper mainlyimprove the corresponding results in [7] and [11].
References
Martinet B: Regularisation d’inéquations variationelles par approximationssuccessives.Rev. Fr. Inform. Rech. Oper. 1970, 4:154–158.
Martinet B: Determination approchée d’un point fixe d’une applicationpseudo-contractante.C. R. Acad. Sci. Paris Sér. A-B 1972, 274:163–165.
Rockafellar RT: Monotone operators and the proximal point algorithm.SIAM J. Control Optim. 1976, 14:877–898. 10.1137/0314056
Rockafellar RT: Augmented Lagrangians and applications of the proximal point algorithm inconvex programming.Math. Oper. Res. 1976, 1:97–116. 10.1287/moor.1.2.97
Lions PL, Mercier B: Splitting algorithms for the sum of two nonlinear operators.SIAM J. Numer. Anal. 1979, 16:964–979. 10.1137/0716071
Passty GB: Ergodic convergence to a zero of the sum of monotone operators in Hilbertspace.J. Math. Anal. Appl. 1979, 72:383–390. 10.1016/0022-247X(79)90234-8
Cho SY, Qin X, Wang L: Strong convergence of a splitting algorithm for treating monotoneoperators.Fixed Point Theory Appl. 2014., 2014: Article ID 94
Zegeye H, Shahzad N: Strong convergence theorem for a common point of solution of variationalinequality and fixed point problem.Adv. Fixed Point Theory 2012, 2:374–397.
Cho SY, Kang SM: On iterative solutions of a common element problem.J. Nonlinear Funct. Anal. 2014., 2014: Article ID 3
Zhang M: An algorithm for treating asymptotically strict pseudocontractions andmonotone operators.Fixed Point Theory Appl. 2014., 2014: Article ID 52
Qin X, Cho SY, Wang L: A regularization method for treating zero points of the sum of two monotoneoperators.Fixed Point Theory Appl. 2014., 2014: Article ID 75
Hecai Y: On weak convergence of an iterative algorithm for common solutions ofinclusion problems and fixed point problems in Hilbert spaces.Fixed Point Theory Appl. 2013., 2013: Article ID 155
Zhao J, Zhang Y, Yang Q: Modified projection methods for the split feasibility problem and themultiple-sets split feasibility problem.Appl. Math. Comput. 2012, 219:1644–1653. 10.1016/j.amc.2012.08.005
Qin X, Cho SY, Wang L: Convergence of splitting algorithms for the sum of two accretive operatorswith applications.Fixed Point Theory Appl. 2014., 2014: Article ID 166
Yu L, Liang M: Convergence of iterative sequences for fixed point and variational inclusionproblems.Fixed Point Theory Appl. 2011., 2011: Article ID 368137
Yang S: Zero theorems of accretive operators in reflexive Banach spaces.J. Nonlinear Funct. Anal. 2013., 2013: Article ID 2
Qin X, Su Y: Approximation of a zero point of accretive operator in Banach spaces.J. Math. Anal. Appl. 2007, 329:415–424. 10.1016/j.jmaa.2006.06.067
Barbu V: Nonlinear Semigroups and Differential Equations in Banach Space. Noordhoff, Groningen; 1976.
Suzuki T: Strong convergence of Krasnoselskii and Mann’s type sequences forone-parameter nonexpansive semigroups without Bochner integrals.J. Math. Anal. Appl. 2005, 305:227–239. 10.1016/j.jmaa.2004.11.017
Liu LS: Ishikawa and Mann iterative process with errors for nonlinear stronglyaccretive mappings in Banach spaces.J. Math. Anal. Appl. 1995, 194:114–125. 10.1006/jmaa.1995.1289
Lopez G, Marquez VM, Wang F, Xu HK: Forward-backward splitting methods for accretive operators in Banachspaces.Abstr. Appl. Anal. 2012., 2012: Article ID 109236
Mainge PE: Strong convergence of projected subgradient methods for nonsmooth andnonstrictly convex minimization.Set-Valued Anal. 2008, 16:899–912. 10.1007/s11228-008-0102-z
Browder FE: Nonexpansive nonlinear operators in a Banach space.Proc. Natl. Acad. Sci. USA 1965, 54:1041–1044. 10.1073/pnas.54.4.1041
Takahashi S, Takahashi W, Toyoda M: Strong convergence theorems for maximal monotone operators with nonlinearmappings in Hilbert spaces.J. Optim. Theory Appl. 2010, 147:27–41. 10.1007/s10957-010-9713-2
Baillon JB, Haddad G: Quelques propriétés des opérateurs angle-bornés etcycliquement monotones.Isr. J. Math. 1977, 26:137–150. 10.1007/BF03007664
Acknowledgements
The author is very grateful to the editor and anonymous reviewers’suggestions which improved the contents of the article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, Y. Some results on a viscosity splitting algorithm in Hilbert spaces. J Inequal Appl 2015, 2 (2015). https://doi.org/10.1186/1029-242X-2015-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2015-2
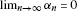 ,
, 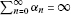 ;
; ;
;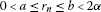 and
and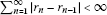 ,
,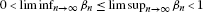 ;
;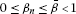 ;
; .
.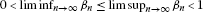 ;
;