- Research
- Open access
- Published:
The strong convergence theorems for split common fixed point problem ofasymptotically nonexpansive mappings in Hilbert spaces
Journal of Inequalities and Applications volume 2015, Article number: 1 (2015)
Abstract
In this paper, an iterative algorithm is introduced to solve the split common fixedpoint problem for asymptotically nonexpansive mappings in Hilbert spaces. Theiterative algorithm presented in this paper is shown to possess strong convergencefor the split common fixed point problem of asymptotically nonexpansive mappingsalthough the mappings do not have semi-compactness. Our results improve and developprevious methods for solving the split common fixed point problem.
MSC: 47H09, 47J25.
1 Introduction and preliminaries
Throughout this paper, let  and
and bereal Hilbert spaces whose inner product and norm are denoted by
bereal Hilbert spaces whose inner product and norm are denoted by  and
and , respectively; let C andQ be nonempty closed convex subsets of
, respectively; let C andQ be nonempty closed convex subsets of  and
and ,respectively. A mapping
,respectively. A mapping  is said to benonexpansive if
is said to benonexpansive if  for any
for any .A mapping
.A mapping  is said to bequasi-nonexpansive if
is said to bequasi-nonexpansive if  for any
for any and
and , where
, where  is the set of fixed pointsof T. A mapping
is the set of fixed pointsof T. A mapping  is calledasymptotically nonexpansive if there exists a sequence
is calledasymptotically nonexpansive if there exists a sequence  satisfying
satisfying  such that
such that  for any
for any .A mapping
.A mapping  is semi-compact if, forany bounded sequence
is semi-compact if, forany bounded sequence  with
with , there exists asubsequence
, there exists asubsequence  such that
such that  converges strongly to somepoint
converges strongly to somepoint  .
.
The split feasibility problem (SFP) is to find a point  with the property
with the property

where  is a bounded linear operator.
is a bounded linear operator.
Assuming that SFP (1.1) is consistent (i.e., (1.1) has a solution), itis not hard to see that  solves(1.1) if and only if it solves the following fixed point equation:
solves(1.1) if and only if it solves the following fixed point equation:

where  and
and arethe (orthogonal) projections onto C and Q, respectively,
arethe (orthogonal) projections onto C and Q, respectively, isany positive constant, and
isany positive constant, and  denotes the adjoint of A.
denotes the adjoint of A.
The SFP in finite-dimensional Hilbert spaces was first introduced by Censor andElfving [1] for modeling inverse problems whicharise from phase retrievals and in medical image reconstruction [2]. Recently, it has been found that the SFP can also beused in various disciplines such as image restoration, computer tomograph, and radiationtherapy treatment planning [2–7].
Let  and
and  be two mappings satisfying
be two mappings satisfying  and
and ,respectively; let
,respectively; let  be a bounded linear operator. The split common fixed point problem (SCFP) formappings S and T is to find a point
be a bounded linear operator. The split common fixed point problem (SCFP) formappings S and T is to find a point  with the property
with the property

We use Γ to denote the set of solutions of SCFP (1.3), that is, .
.
Since each closed and convex subset may be considered as a fixed point set of aprojection on the subset, hence the split common fixed point problem (SCFP) isa generalization of the split feasibility problem (SFP) and the convexfeasibility problem (CFP) [5].
Split feasibility problems and split common fixed point problems have been studied bysome authors [8–15]. In 2010,Moudafi [10] proposed the following iterationmethod to approximate a split common fixed point of demi-contractive mappings: forarbitrarily chosen  ,
,

and he proved that  converges weakly to a split common fixedpoint
converges weakly to a split common fixedpoint  , where
, where and
and  are two demi-contractive mappings,
are two demi-contractive mappings,  is a bounded linear operator.
is a bounded linear operator.
Using the iterative algorithm above, in 2011, Moudafi [9] also obtained a weak convergence theorem for the split commonfixed point problem of quasi-nonexpansive mappings in Hilbert spaces. After that, someauthors also proposed some iterative algorithms to approximate a split common fixedpoint of other nonlinear mappings, such as nonspreading type mappings [16], asymptotically quasi-nonexpansive mappings[12], κ-asymptoticallystrictly pseudononspreading mappings [17],asymptotically strictly pseudocontraction mappings [18]etc., but they just obtained weak convergence theoremswhen those mappings do not have semi-compactness. This naturally brings us to thefollowing question.
Can we construct an iterative scheme which can guarantee the strong convergence forsplit common fixed point problems without assumption ofsemi-compactness?
In this paper, we introduce the following iterative scheme. Let  ,
, ,the sequence
,the sequence  is defined as follows:
is defined as follows:

where  and
and  are two asymptotically nonexpansive mappings,
are two asymptotically nonexpansive mappings,  is a bounded linear operator,
is a bounded linear operator,  denotes the adjoint of A. Under some suitable conditions on parameters, theiterative scheme
denotes the adjoint of A. Under some suitable conditions on parameters, theiterative scheme  is shown to converge strongly to a splitcommon fixed point of asymptotically nonexpansive mappings
is shown to converge strongly to a splitcommon fixed point of asymptotically nonexpansive mappings  and
and without the assumption of semi-compactness on
without the assumption of semi-compactness on  and
and .
.
The following lemma and results are useful for our proofs.
Lemma 1.1[19]
LetEbe a real uniformly convex Banach space, Kbea nonempty closed subset ofE, and let be an asymptoticallynonexpansive mapping. Then
be an asymptoticallynonexpansive mapping. Then isdemiclosed at zero, that is, if
isdemiclosed at zero, that is, if convergesweakly to a point
convergesweakly to a point and
and ,then
,then .
.
Let C be a closed convex subset of a real Hilbert space H. denotes the metric projection of H onto C. It is well known that
denotes the metric projection of H onto C. It is well known that ischaracterized by the properties: for
ischaracterized by the properties: for  and
and ,
,

and

In a real Hilbert space H, it is also well known that

and

2 Main results
Theorem 2.1Let and
and be twoHilbert spaces,
be twoHilbert spaces,  bea bounded linear operator,
bea bounded linear operator,  bean asymptotically nonexpansive mapping with the sequence
bean asymptotically nonexpansive mapping with the sequence satisfying
satisfying ,and
,and bean asymptotically nonexpansive mapping with the sequence
bean asymptotically nonexpansive mapping with the sequence satisfying
satisfying ,
, and
and , respectively.Let
, respectively.Let ,
, ,and let the sequence
,and let the sequence be defined as follows:
be defined as follows:

where denotesthe adjoint ofA,
denotesthe adjoint ofA,  and
and satisfies
satisfies ,
,  ,
,  .If
.If , then
, then converges stronglyto
converges stronglyto .
.
Proof We will divide the proof into five steps.
Step 1. We first show that  is closedand convex for any
is closedand convex for any  .
.
Since  ,so
,so  isclosed and convex. Assume that
isclosed and convex. Assume that  is closedand convex. For any
is closedand convex. For any  ,since
,since

we know that  is closed and convex. Therefore
is closed and convex. Therefore  is closedand convex for any
is closedand convex for any  .
.
Step 2. We prove  for any
for any  .
.
Let  , then from (2.1) we have
, then from (2.1) we have

where

Substituting (2.3) into (2.2), we can obtain that

In addition, it follows from (2.1) that

Therefore, from (2.4) and (2.5), we know that  and
and  for any
for any  .
.
Step 3. We will show that  is a Cauchy sequence.
is a Cauchy sequence.
Since  and
and  ,then
,then

It means that  is bounded. For any
is bounded. For any  , by using(1.6), we have
, by using(1.6), we have

which implies that  . Thus
. Thus is nondecreasing. Therefore, by the boundednessof
is nondecreasing. Therefore, by the boundednessof  ,
,  exists. For somepositive integers m, n with
exists. For somepositive integers m, n with  , from
, from and (1.6), we have
and (1.6), we have

Since  exists, it followsfrom (2.7) that
exists, it followsfrom (2.7) that  . Therefore
. Therefore is a Cauchy sequence.
is a Cauchy sequence.
Step 4. We will show that  .
.
Since  ,we have
,we have



Notice that  , it follows from (2.4)that
, it follows from (2.4)that

thus, since  is bounded and
is bounded and  ,from (2.8) we have
,from (2.8) we have

On the other hand, since

we have

Since  and
and  ,we know that
,we know that

In addition, since  , we know that
, we know that . So from
. So from

we can obtain that

Similarly, we have

Step 5. We will show that  converges strongly to an element ofΓ.
converges strongly to an element ofΓ.
Since  is a Cauchy sequence, we may assume that
is a Cauchy sequence, we may assume that ,from (2.8) we have
,from (2.8) we have  ,which implies that
,which implies that  .So it follows from (2.13) and Lemma 1.1 that
.So it follows from (2.13) and Lemma 1.1 that  .
.
In addition, since A is a bounded linear operator, we have that . Hence, itfollows from (2.14) and Lemma 1.1 that
. Hence, itfollows from (2.14) and Lemma 1.1 that  . This means that
. This means that and
and converges strongly to
converges strongly to . The proof iscompleted. □
. The proof iscompleted. □
In Theorem 2.1, as  and
and  ,we have the following result.
,we have the following result.
Corollary 2.2Let be aHilbert space,
be aHilbert space,  bean asymptotically nonexpansive mapping with a sequence
bean asymptotically nonexpansive mapping with a sequence satisfying
satisfying .The sequence
.The sequence is defined as follows:
is defined as follows: ,
,

where and
and satisfies
satisfies .If
.If , then
, then converges strongly to a fixedpoint
converges strongly to a fixedpoint ofT.
ofT.
In Theorem 2.1, when  and
and aretwo nonexpansive mappings, the following result holds.
aretwo nonexpansive mappings, the following result holds.
Corollary 2.3Let and
and be twoHilbert spaces,
be twoHilbert spaces,  bea bounded linear operator,
bea bounded linear operator,  and
and betwo nonexpansive mappings such that
betwo nonexpansive mappings such that and
and , respectively.Let
, respectively.Let ,
, ,and let the sequence
,and let the sequence be defined as follows:
be defined as follows:

where denotesthe adjoint ofA,
denotesthe adjoint ofA,  and
and satisfies
satisfies .If
.If , then
, then converges stronglyto
converges stronglyto .
.
Remark 2.4 When  and
and aretwo quasi-nonexpansive mappings and
aretwo quasi-nonexpansive mappings and  and
and  are demiclosed at zero, Corollary 2.3 also holds.
are demiclosed at zero, Corollary 2.3 also holds.
Example 2.5 Let C be a unit ball in a real Hilbert space ,and let
,and let  be amapping defined by
be amapping defined by

It is proved in Goebel and Kirk [20] that
-
(i)
 ,
, 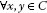 ;
; -
(ii)
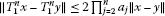 ,
, 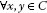 ,
,  .
.
Taking  ,
, , itis easy to see that
, itis easy to see that  .So we can take
.So we can take  ,and
,and  ,
, ,then
,then

Therefore  is anasymptotically nonexpansive mapping from C into itself with
is anasymptotically nonexpansive mapping from C into itself with .
.
Let D be an orthogonal subspace of  with thenorm
with thenorm  and the inner product
and the inner product  for
for  and
and  . For each
. For each , we define amapping
, we define amapping  by
by

It is easy to show that  or
or for any
for any .Therefore
.Therefore  is anasymptotically nonexpansive mapping from D into itself with
is anasymptotically nonexpansive mapping from D into itself with since
since for anysequence
for anysequence  with
with .
.
Obviously, C and D are closed convex subsets of and
and ,respectively. Let
,respectively. Let  be defined by
be defined by for
for  . ThenA is a bounded linear operator with adjoint operator
. ThenA is a bounded linear operator with adjoint operator  for
for  . Clearly,
. Clearly, ,
,  .
.
Taking  ,
, ,
, ,
, ,
, and
and  ,
, . Itfollows from Theorem 2.1 that
. Itfollows from Theorem 2.1 that  converges strongly to
converges strongly to .
.
3 Applications and examples
Application to the equilibrium problem
Let H be a real Hilbert space, C be a nonempty closed and convexsubset of H, and let the bifunction  satisfy the following conditions:
satisfy the following conditions:
(A1)  ,
, ;
;
(A2)  ,
, ;
;
(A3) For all  ,
, ;
;
(A4) For each  , thefunction
, thefunction  is convex and lower semi-continuous.
is convex and lower semi-continuous.
The so-called equilibrium problem for F is to find a point such that
such that  for all
for all .The set of its solutions is denoted by
.The set of its solutions is denoted by 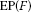 .
.
Lemma 3.1[21]
LetCbe a nonempty closed convex subset of a HilbertspaceH, and let be a bifunctionsatisfying (A1)-(A4). Let
be a bifunctionsatisfying (A1)-(A4). Let and
and .Then there exists
.Then there exists suchthat
suchthat

Lemma 3.2[21]
Assume that satisfies(A1)-(A4). For
satisfies(A1)-(A4). For and
and ,define a mapping
,define a mapping as follows:
as follows:

Then
-
(1)
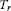 is single-valued;
is single-valued; -
(2)
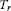 is firmly nonexpansive, that is, for all
is firmly nonexpansive, that is, for all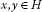 ,
, 
-
(3)
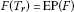 ;
; -
(4)
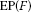 is nonempty, closed and convex.
is nonempty, closed and convex.
Theorem 3.3Let and
and be twoHilbert spaces,
be twoHilbert spaces,  bea bounded linear operator,
bea bounded linear operator,  bea nonexpansive mapping,
bea nonexpansive mapping,  be a bifunctionsatisfying (A1)-(A4). Assume that
be a bifunctionsatisfying (A1)-(A4). Assume that and
and .Taking
.Taking ,for arbitrarily chosen
,for arbitrarily chosen ,the sequence
,the sequence is defined asfollows:
is defined asfollows:

where denotesthe adjoint ofA,
denotesthe adjoint ofA,  ,
, and
and satisfies
satisfies .If
.If , then thesequence
, then thesequence converges strongly toa point
converges strongly toa point .
.
Proof It follows from Lemma 3.2 that  ,
, 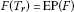 is nonempty, closed and convex and
is nonempty, closed and convex and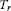 is a firmly nonexpansive mapping. Hence all conditions in Corollary 2.3 aresatisfied. The conclusion of Theorem 3.3 can be directly obtained fromCorollary 2.3. □
is a firmly nonexpansive mapping. Hence all conditions in Corollary 2.3 aresatisfied. The conclusion of Theorem 3.3 can be directly obtained fromCorollary 2.3. □
Let  and
and  be two real Hilbert spaces. Let C be a closed convex subset of
be two real Hilbert spaces. Let C be a closed convex subset of ,K be a closed convex subset of
,K be a closed convex subset of  ,
, be a bounded linear operator. Assume that F is a bi-function from
be a bounded linear operator. Assume that F is a bi-function from into R and G is a bi-function from
into R and G is a bi-function from  intoR. The split equilibrium problem (SEP) is to
intoR. The split equilibrium problem (SEP) is to

and

Let  denote the solution setof the split equilibrium problem SEP.
denote the solution setof the split equilibrium problem SEP.
Example 3.4[22]
Let  ,
, and
and  . Let
. Let for all R, then A is a bounded linear operator. Let
for all R, then A is a bounded linear operator. Let and
and bedefined by
bedefined by  and
and  , respectively. Clearly,
, respectively. Clearly, and
and . So
. So  .
.
Example 3.5[22]
Let  with the standard norm
with the standard norm  and
and with the norm
with the norm  for some
for some  .
. and
and  . Define a bi-function
. Define a bi-function ,where
,where  ,
,  , thenF is a bi-function from
, thenF is a bi-function from  intoR with
intoR with  . For each
. For each ,let
,let  ,then A is a bounded linear operator from
,then A is a bounded linear operator from  into
into .In fact, it is also easy to verify that
.In fact, it is also easy to verify that  and
and for some
for some  and
and  .Now define another bi-function G as follows:
.Now define another bi-function G as follows:  for all
for all  .Then G is a bi-function from
.Then G is a bi-function from  intoR with
intoR with  .
.
Clearly, when  , we have
, we have  . So
. So  .
.
Corollary 3.6Let and
and be twoHilbert spaces,
be twoHilbert spaces,  bea bounded linear operator,
bea bounded linear operator,  be a bifunctionsatisfying
be a bifunctionsatisfying and
and be a bifunctionsatisfying
be a bifunctionsatisfying .Taking
.Taking ,for arbitrarily chosen
,for arbitrarily chosen ,the sequence
,the sequence is defined asfollows:
is defined asfollows:

where denotesthe adjoint ofA,
denotesthe adjoint ofA,  ,
, and
and satisfies
satisfies .If
.If , then thesequence
, then thesequence converges strongly toa point
converges strongly toa point .
.
Remark 3.7 Since Example 3.4 and Example 3.5 satisfy the conditionsof Corollary 2.3, the split equilibrium problems in Example 3.4 andExample 3.5 can be solved by algorithm (3.4).
Application to the hierarchial variational inequality problem
Let H be a real Hilbert space,  and
and be two nonexpansive mappings from H to H such that
be two nonexpansive mappings from H to H such that and
and  .
.
The so-called hierarchical variational inequality problem for nonexpansive mapping with respect to a nonexpansive mapping
with respect to a nonexpansive mapping  isto find a point
isto find a point  such that
such that

It is easy to see that (3.5) is equivalent to the following fixed point problem:

where  is the metric projection from H onto
is the metric projection from H onto  . Letting
. Letting and
and (the fixed point set ofthe mapping
(the fixed point set ofthe mapping  )and
)and  (theidentity mapping on H), then problem (3.6) is equivalent to the followingsplit feasibility problem:
(theidentity mapping on H), then problem (3.6) is equivalent to the followingsplit feasibility problem:

Hence from Theorem 2.1 we have the following theorem.
Theorem 3.8LetH,  ,
, ,CandQbe the same as above.Let
,CandQbe the same as above.Let and
and ,and let the sequence
,and let the sequence be defined asfollows:
be defined asfollows:

where and
and satisfies
satisfies .If
.If , then thesequence
, then thesequence converges strongly toa solution of the hierarchical variational inequality problem (3.5).
converges strongly toa solution of the hierarchical variational inequality problem (3.5).
References
Byrne C: Iterative oblique projection onto convex subsets and the split feasibilityproblems.Inverse Probl. 2002, 18:441–453. 10.1088/0266-5611/18/2/310
Censor Y, Elfving T: A multiprojection algorithm using Bregman projection in a product space.Numer. Algorithms 1994, 8:221–239. 10.1007/BF02142692
Censor Y, Elfving T, Kopf N, Bortfeld T: The multiple-sets split feasibility problem and its applications.Inverse Probl. 2005, 21:2071–2084. 10.1088/0266-5611/21/6/017
Censor Y, Seqal A: The split common fixed point problem for directed operators.J. Convex Anal. 2009, 16:587–600.
Censor Y, Bortfeld T, Martin B, Trofimov T: A unified approach for inversion problem in intensity-modulated radiationtherapy.Phys. Med. Biol. 2006, 51:2353–2365. 10.1088/0031-9155/51/10/001
Censor Y, Motova A, Segal A: Perturbed projections and subgradient projections for the multiple-sets splitfeasibility problems.J. Math. Anal. Appl. 2007, 327:1244–1256. 10.1016/j.jmaa.2006.05.010
Lopez G, Martin V, Xu HK: Iterative algorithms for the multiple-sets split feasibility problem. In Biomedical Mathematics: Promising Directions in Imaging, Therapy Planning andInverse Problems. Edited by: Censor Y, Jiang M, Wang G. Medical Physics Publishing, Madison; 2009:243–279.
Dang Y, Gao Y: The strong convergence of a KM-CQ-like algorithm for a split feasibilityproblem.Inverse Probl. 2011., 27: Article ID 015007
Moudafi A: A note on the split common fixed point problem for quasi-nonexpansiveoperators.Nonlinear Anal. 2011, 74:4083–4087. 10.1016/j.na.2011.03.041
Moudafi A: The split common fixed point problem for demi-contractive mappings.Inverse Probl. 2010., 26: Article ID 055007
Maruster S, Popirlan C: On the Mann-type iteration and convex feasibility problem.J. Comput. Appl. Math. 2008, 212:390–396. 10.1016/j.cam.2006.12.012
Qin LJ, Wang L, Chang SS: Multiple-set split feasibility problem for a finite family of asymptoticallyquasi-nonexpansive mappings.Panam. Math. J. 2012,22(1):37–45.
Wang F, Xu HK: Approximation curve and strong convergence of the CQ algorithm for the splitfeasibility problem.J. Inequal. Appl. 2010., 2010: Article ID 102085 10.1155/2010/102085
Xu HK: A variable Krasnosel’skii-Mann algorithm and the multiple-set splitfeasibility problem.Inverse Probl. 2006, 22:2021–2034. 10.1088/0266-5611/22/6/007
Yang Q: The relaxed CQ algorithm for solving the split feasibility problem.Inverse Probl. 2004, 20:1261–1266. 10.1088/0266-5611/20/4/014
Chang SS, Kim JK, Cho YJ, Sim JY: Weak-and strong-convergence theorems of solution to split feasibility problem fornonspreading type mapping in Hilbert spaces.Fixed Point Theory Appl. 2014., 2014: Article ID 11
Quan J, Chang SS, Zhang X: Multiple-set split feasibility problems fork-strictly pseudononspreadingmapping in Hilbert spaces.Abstr. Appl. Anal. 2013., 2013: Article ID 342545 10.1155/2013/342545
Chang SS, Cho YJ, Kim JK, Zhang WB, Yang L: Multiple-set split feasibility problems for asymptotically strictpseudocontractions.Abstract and Applied Analysis 2012., 2012: Article ID 491760 10.1155/2012/491760
Chang SS, Cho YJ, Zhou H: Demi-closed principle and weak convergence problems for asymptoticallynonexpansive mappings.J. Korean Math. Soc. 2001, 38:1245–1260.
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings.Proc. Am. Math. Soc. 1972, 35:171–174. 10.1090/S0002-9939-1972-0298500-3
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces.J. Nonlinear Convex Anal. 2005, 6:117–136.
He Z: The split equilibrium problem and its convergence algorithms.J. Inequal. Appl. 2012., 2012: Article ID 162
Acknowledgements
The authors would like to express their thanks to the reviewers and editors for theirhelpful suggestions and advice. This work was supported by the National NaturalScience Foundation of China (Grant No. 11361070) and the Scientific ResearchFoundation of Postgraduate of Yunnan University of Finance and Economics.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to this work. All authors read and approved the finalmanuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, XF., Wang, L., Ma, Z.L. et al. The strong convergence theorems for split common fixed point problem ofasymptotically nonexpansive mappings in Hilbert spaces. J Inequal Appl 2015, 1 (2015). https://doi.org/10.1186/1029-242X-2015-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2015-1
 ,
, 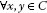 ;
;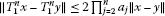 ,
,  .
.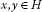 ,
, 