- Research
- Open access
- Published:
On properties of k-quasi-class operators
Journal of Inequalities and Applications volume 2014, Article number: 91 (2014)
Abstract
Let n and k be positive integers; an operator is called a k-quasi-class operator if , which is a common generalization of class A and class operators. In this paper, firstly we prove some basic structural properties of this class of operators, showing that if T is a k-quasi-class operator, then the nonzero points of its point spectrum and joint point spectrum are identical, the eigen-spaces corresponding to distinct eigenvalues of T are mutually orthogonal, the nonzero points of its approximate point spectrum and joint approximate point spectrum are identical; secondly we consider the tensor products for k-quasi-class operators, giving a necessary and sufficient condition for to be a k-quasi-class operator when T and S are both nonzero operators.
MSC:47B20, 47A63.
1 Introduction
Let ℋ be a separable complex Hilbert space and  be the set of complex numbers. Let denote the -algebra of all bounded linear operators acting on ℋ. Recall that is called p-hyponormal for if [1]; when , T is called hyponormal. T is called paranormal if for all [2, 3]. T is called normaloid if for all (equivalently, , the spectral radius of T). In order to discuss the relations between paranormal and p-hyponormal and log-hyponormal operators (T is invertible and ), Furuta et al. [4] introduced a very interesting class of operators: class A defined by , where , which is called the absolute value of T and they showed that class A is a subclass of paranormal and contains p-hyponormal and log-hyponormal operators. Recently Yuan and Gao [5] introduced class (i.e., ) operators and n-paranormal operators (i.e., for every unit vector ) for some positive integer n. For more interesting properties on class and n-paranormal operators, see [6–8].
be the set of complex numbers. Let denote the -algebra of all bounded linear operators acting on ℋ. Recall that is called p-hyponormal for if [1]; when , T is called hyponormal. T is called paranormal if for all [2, 3]. T is called normaloid if for all (equivalently, , the spectral radius of T). In order to discuss the relations between paranormal and p-hyponormal and log-hyponormal operators (T is invertible and ), Furuta et al. [4] introduced a very interesting class of operators: class A defined by , where , which is called the absolute value of T and they showed that class A is a subclass of paranormal and contains p-hyponormal and log-hyponormal operators. Recently Yuan and Gao [5] introduced class (i.e., ) operators and n-paranormal operators (i.e., for every unit vector ) for some positive integer n. For more interesting properties on class and n-paranormal operators, see [6–8].
Let ℋ, 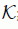 be complex Hilbert spaces and the tensor product of ℋ,
be complex Hilbert spaces and the tensor product of ℋ, 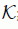 ; i.e., the completion of the algebraic tensor product of ℋ,
; i.e., the completion of the algebraic tensor product of ℋ, 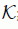 with the inner product for , . Let and . denotes the tensor product of T and S; i.e., for , .
with the inner product for , . Let and . denotes the tensor product of T and S; i.e., for , .
Definition 1.1 is called a k-quasi-class operator for positive integers n and k if
In general, the following implications hold:
In this paper, firstly we prove some basic structural properties of this class of operators, showing that if T is a k-quasi-class operator, then the nonzero points of its point spectrum and joint point spectrum are identical, the eigen-spaces corresponding to distinct eigenvalues of T are mutually orthogonal, the nonzero points of its approximate point spectrum and joint approximate point spectrum are identical; secondly we consider the tensor products for k-quasi-class operators, giving a necessary and sufficient condition for to be a k-quasi-class operator when T and S are both nonzero operators.
2 The basic properties for k-quasi-class operators
In the following lemma, we study the matrix representation of a k-quasi-class operator with respect to the direct sum of and its orthogonal complement.
Lemma 2.1 Let be a k-quasi-class operator for positive integers n and k, and let on be matrix expression. Assume that is not dense, then is a class operator on and . Furthermore, .
Proof Consider the matrix representation of T with respect to the decomposition : . Let P be the orthogonal projection of ℋ onto . Then . Since T is a k-quasi-class operator, we have
Then
by Hansen’s inequality [9]. On the other hand
Hence
That is, is a class operator on .
For any ,
which implies .
Since , where  is the union of the holes in , which happen to be a subset of by [[10], Corollary 7], , and has no interior points, we have .
is the union of the holes in , which happen to be a subset of by [[10], Corollary 7], , and has no interior points, we have .
In [6], Yuan and Ji introduced -quasiparanormal operators. is called a -quasiparanormal operator for positive integers n and k if
for . □
In the following we give the relations between -quasiparanormal and k-quasi-class operators.
Theorem 2.2 Let T be a k-quasi-class operator for positive integers n and k. Then T is a -quasiparanormal operator.
To give a proof of Theorem 2.2, the following famous inequality is needed.
Lemma 2.3 (Hölder-McCarthy’s inequality [11])
Let . Then the following assertions hold:
-
(1)
for and all .
-
(2)
for and all .
Proof of Theorem 2.2 Suppose that T is k-quasi-class operator. Then
Let . Then by Hölder-McCarthy’s inequality, we have
So we have
hence T is a -quasiparanormal operator. □
Remark We give an example which is -quasiparanormal, but not k-quasi-class .
Example 2.4 Let . Then T is -quasiparanormal, but not k-quasi-class .
By simple calculation we have
Hence T is not k-quasi-class . However, for all ,
By arithmetic-geometric mean inequality, we have
for all . Therefore T is -quasiparanormal by [[6], Lemma 2.2].
Theorem 2.5 Let be a k-quasi-class operator for positive integers k and n. If is an invariant subspace of T, then the restriction is also a k-quasi-class operator.
Proof Let P be the orthogonal projection of ℋ onto ℳ, and let . Then and . Since T is a k-quasi-class operator, we have
Since
by Hansen’s inequality and
we have
that is, is also a k-quasi-class operator. □
In the following, we shall show that if T is a k-quasi-class operator, then the nonzero points of its point spectrum and joint point spectrum are identical, the eigen-spaces corresponding to distinct eigenvalues of T are mutually orthogonal, the nonzero points of its approximate point spectrum and joint approximate point spectrum are identical.
Theorem 2.6 Let be a k-quasi-class operator for positive integers n and k. If and for some , then .
Proof We may assume that . Let be a span of . Then is an invariant subspace of T and
Let P be the orthogonal projection of ℋ onto . It suffices to show that in (2.2). Since T is a k-quasi-class operator and , we have
We remark
Then by Hansen’s inequality and (2.3), we have
Hence we may write
We have
This implies and . On the other hand, by simple calculation we have
Hence
and
Since T is a k-quasi-class operator, by simple calculation we have
where is a positive operator. Recall that if and only if and for some contraction W. Thus we have
by . By (2.4) and (2.5), we have . This completes the proof. □
Corollary 2.7 Let be a k-quasi-class operator for positive integers n and k. Then the following assertions hold:
-
(1)
.
-
(2)
If , , and , then .
Proof (1) Clearly by Theorem 2.6.
-
(2)
Without loss of generality, we assume . Then we have by Theorem 2.6.
Thus we have . Since , . □
Theorem 2.8 Let be a k-quasi-class operator for positive integers n and k. Then .
To prove Theorem 2.8, we need the following auxiliary results.
Lemma 2.9 (see [12])
Let ℋ be a complex Hilbert space. Then there exists a Hilbert space 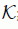 such that and a map such that:
such that and a map such that:
-
(1)
φ is a faithful ∗-representation of the algebra on
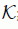 .
. -
(2)
for any in .
-
(3)
for any .
Lemma 2.10 (see [13])
Let be Berberian’s faithful ∗-representation. Then .
Proof of Theorem 2.8 Let be Berberian’s faithful ∗-representation of Lemma 2.9. In the following, we shall show that is also a k-quasi-class operator for positive integers n and k. In fact, since T is a k-quasi-class operator, we have
Hence we have
The proof is complete. □
If T satisfies for some complex λ, then for any positive integer n.
An operator is said to have finite ascent if for some positive integer n.
Theorem 2.12 Let be a k-quasi-class operator for positive integers n and k. Then has finite ascent for all complex number λ.
Proof By Theorem 2.2, we see that T is a -quasiparanormal operator. So has finite ascent for all complex number λ by [[6], Theorem 4.1]. □
3 Tensor products for k-quasi-class operators
Let denote the tensor product on the product space for nonzero and . The operation of taking tensor products preserves many properties of and , but by no means all of them. For example the normaloid property is invariant under tensor products, the spectraloid property is not (see [[15], pp.623 and 631]); and is normal if and only if T and S are normal [16, 17]; however, there exist paranormal operators and such that is not paranormal [18]. Duggal [19] showed that for nonzero and , is p-hyponormal if and only if T, S are p-hyponormal. This result was extended to p-quasihyponormal operators, class A operators, ∗-class A operators, log-hyponormal operators and class operators (, ) in [20–23], respectively. The following theorem gives a necessary and sufficient condition for to be a k-quasi-class operator when T and S are both nonzero operators.
Theorem 3.1 Let and be nonzero operators. Then is a k-quasi-class operator if and only if one of the following assertions holds:
-
(1)
or .
-
(2)
T and S are k-quasi-class operators.
Proof It is clear that is a k-quasi-class operator if and only if
Therefore the sufficiency is clear.
To prove the necessary. Suppose that is a k-quasi-class operator. Let and be arbitrary. Then we have
It suffices to prove that if (1) does not hold, then (2) holds. Suppose that and . To the contrary, assume that T is not a k-quasi-class operator, then there exists such that
and
From (3.1) we have
for all , that is,
for all . Therefore S is a k-quasi-class operator. From Lemma 2.1 we can write on , where is a class operator. Let P be the orthogonal projection of 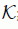 onto . By the proof of Lemma 2.1, we have
onto . By the proof of Lemma 2.1, we have
So we have
for all by (3.2). Hence,
for all .
Taking the supremum over all , we have
by (3.3). Since self-adjoint operators are normaloid, we have
Hence we have
By (3.4) and (3.6) we have
This implies that . Since for all , we have . This contradicts the assumption . Hence T must be a k-quasi-class operator. A similar argument shows that S is also a k-quasi-class operator. The proof is complete. □
References
Aluthge A: On p -hyponormal operators for . Integral Equ. Oper. Theory 1990, 13: 307-315. 10.1007/BF01199886
Furuta T: On the class of paranormal operators. Proc. Jpn. Acad. 1967, 43: 594-598. 10.3792/pja/1195521514
Furuta T: Invitation to Linear Operators. Taylor & Francis, London; 2001.
Furuta T, Ito M, Yamazaki T: A subclass of paranormal operators including class of log-hyponormal and several classes. Sci. Math. 1998,1(3):389-403.
Yuan JT, Gao ZS: Weyl spectrum of class and n -paranormal operators. Integral Equ. Oper. Theory 2008, 60: 289-298. 10.1007/s00020-008-1556-y
Yuan JT, Ji GX:On -quasiparanormal operators. Stud. Math. 2012,209(3):289-301. 10.4064/sm209-3-6
Gao, FG, Li, XC: Generalized Weyl’s theorem and spectral continuity for -quasiparanormal operators (to appear)
Kubrusly CS, Duggal BP: A note on k -paranormal operators. Oper. Matrices 2010, 4: 213-223.
Hansen F: An inequality. Math. Ann. 1980, 246: 249-250. 10.1007/BF01371046
Han JK, Lee HY, Lee WY:Invertible completions of upper triangular operator matrices. Proc. Am. Math. Soc. 2000,128(1):119-123. 10.1090/S0002-9939-99-04965-5
McCarthy CA:. Isr. J. Math. 1967, 5: 249-271. 10.1007/BF02771613
Berberian SK: Approximate proper vectors. Proc. Am. Math. Soc. 1962, 13: 111-114. 10.1090/S0002-9939-1962-0133690-8
Xia D: Spectral Theory of Hyponormal Operators. Birkhäuser, Boston; 1983.
Uchiyama A: On the isolated points of the spectrum of paranormal operators. Integral Equ. Oper. Theory 2006, 55: 291-298.
Saitô T Lecture Notes in Mathematics 247. In Hyponormal Operators and Related Topics. Springer, Berlin; 1971.
Hou JC: On tensor products of operators. Acta Math. Sin. New Ser. 1993, 9: 195-202. 10.1007/BF02560050
Stochel J: Seminormality of operators from their tensor products. Proc. Am. Math. Soc. 1996, 124: 435-440.
Ando T: Operators with a norm condition. Acta Sci. Math. 1972, 33: 169-178.
Duggal BP: Tensor products of operators-strong stability and p -hyponormality. Glasg. Math. J. 2000, 42: 371-381.
Jeon IH, Duggal BP: On operators with an absolute value condition. J. Korean Math. Soc. 2004, 41: 617-627.
Duggal BP, Jeon IH, Kim IH: On ∗-paranormal contractions and property for ∗-class A operators. Linear Algebra Appl. 2012, 436: 954-962. 10.1016/j.laa.2011.06.002
Kim IH: Tensor products of log-hyponormal operators. Bull. Korean Math. Soc. 2005, 42: 269-277.
Tanahashi K:Tensor products of log-hyponormal operators and of class operators. Glasg. Math. J. 2004, 46: 91-95. 10.1017/S0017089503001563
Acknowledgements
This research is supported by the National Natural Science Foundation of China (11301155), (11271112), the Natural Science Foundation of the Department of Education, Henan Province (2011A110009), (13B110077), the Youth Science Foundation of Henan Normal University and the new teachers Science Foundation of Henan Normal University (No. qd12102).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of the present article. They also read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, X., Gao, F. On properties of k-quasi-class operators. J Inequal Appl 2014, 91 (2014). https://doi.org/10.1186/1029-242X-2014-91
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2014-91