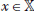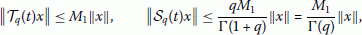- Research
- Open access
- Published:
Controllability problem for fractional integrodifferential evolution systems of mixed type with the measure of noncompactness
Journal of Inequalities and Applications volume 2014, Article number: 292 (2014)
Abstract
We consider the controllability problem for a class of fractional evolution systems of mixed type in an infinite dimensional Banach space. The existence of mild solutions and controllability results are discussed by a new estimation technique of the measure of noncompactness and a fixed point theorem with respect to a convex-power condensing operator. However, the main results do not need any restrictive conditions on estimated parameters of the measure of noncompactness. Since we do not assume that the semigroup is compact and other conditions are more general, the outcomes we obtain here improve and generalize many known controllability results. An example is also given to demonstrate the applications of our main results.
MSC:26A33, 34B15, 93B05, 93C25.
1 Introduction
The concept of controllability was firstly introduced by Kalman in 1960. There has been a significant development in controllability results of systems represented by differential equations, integrodifferential equations, impulsive equations, differential inclusions, neutral differential equations and delay differential equations in Banach spaces. Most of the previous results require the assumption that the operator semigroup is compact. Using a compact analytic semigroup and a nonlinear alterative of Leray-Schauder type for multivalued maps due to O’Regan, Yan [1] established sufficient conditions for the controllability of fractional order partial neutral functional integrodifferential inclusion with infinite delay. Balachandran and Park [2] studied the controllability of fractional integrodifferential systems in Banach spaces, and an example with a compact analytic semigroup was also given. Based upon Bohnenblust-Karlin’s fixed point theorem and a compact semigroup, Chang [3] investigated a controllability result of mixed Volterra-Fredholm type integrodifferential inclusions in Banach spaces. Chalishajar [4] considered sufficient conditions for semilinear mixed Volterra-Fredholm type integrodifferential systems in a Banach space via a compact semigroup. Hernández and O’Regan [5] pointed out that the controllability results will be restricted to the finite dimensional space when the compactness of a semigroup and some other assumptions are satisfied. So, many researchers have tried to get sufficient conditions guaranteeing the controllability results of various systems without involving the compactness of a semigroup.
Wang et al. [6] studied the following fractional neutral differential system in an abstract space:
By using the fractional power of operators and Sadovskii’s fixed point theorem, they obtained the complete controllability of fractional neutral differential systems in an abstract space without involving the compactness of characteristic solution operators, but the main results require that the set is relatively in a Banach space  for arbitrary and (see () in [6]).
for arbitrary and (see () in [6]).
Fec̆kan et al. [7] discussed the controllability of a class of fractional functional evolution equations of Sobolev type
in a Banach space. With the help of two new characteristic solution operators and their properties, such as compactness and boundedness, the controllability results for fractional evolution equations were obtained by the Schauder fixed point theorem. Later, researchers have always tried to avoid the compactness of a semigroup via the measure of noncompactness. Ji et al.[8] considered the controllability of impulsive functional differential equations with nonlocal conditions by the measure of noncompactness and the Mönch fixed point theorem. Machado et al. [9] obtained the controllability results for a class of abstract impulsive mixed-type functional integrodifferential equations with finite delay in Banach spaces, sufficient conditions for controllability were obtained by the Mönch fixed point theorem via the measure of noncompactness and semigroup theory. Those results in [8, 9] do not assume the compactness of the evolution system, but restrictive conditions on the estimated parameter of the measure of noncompactness are required.
By using the techniques of convex-power condensing operators, Zhu et al. [10] considered the existence of mild solutions for one order impulsive semilinear differential equations with nonlocal conditions. Xue [11] obtained the existence results of integral solutions for nonlinear one order differential equations with nonlocal initial value conditions under the assumptions of the measure of noncompactness in a separable and uniformly smooth Banach space. Ahmad et al. [12] showed the existence of mild solutions to one order impulsive integrodifferential equations with the nonlinearity of a form , where represents a Volterra-type integral operator. Very recently, Wang and Zhou [13] investigated the complete controllability of fractional semilinear systems in infinite dimensional spaces of the type
Chen and Li [14] studied a nonlocal problem for fractional evolution equations of mixed type in a Banach space, the existence of mild solutions and positive mild solutions was obtained by utilizing the measure of noncompactness and a new fixed point theorem.
Inspired by the above results, here we consider the controllability of the following fractional evolution system of mixed type in an infinite dimensional Banach space  :
:
where is the Caputo fractional derivative. , is a closed linear operator and −A generates a uniformly bounded -semigroup in 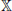 . f and g will be specified later. is a bounded linear operator, , and integral operators S and T are defined as
. f and g will be specified later. is a bounded linear operator, , and integral operators S and T are defined as
Here , , and , .
In the present paper, we introduce a suitable concept of mild solutions for abstract control system (1.1). Under some necessary conditions on the characteristic solution operators and , we obtain the sufficient conditions of controllability results for system (1.1) when the operator , , is not compact. The methods we use are a new estimation technique of the measure of noncompactness and a fixed point theorem with respect to a convex-power condensing operator. The main results do not require any restrictive conditions on estimated parameters of the measure of noncompactness, i.e., parameters () do not appear in inequality (3.1) and any other inequalities, which is the main difference between our study and the previous results, and also the main contribution of this paper.
The rest of the paper is organized as follows. In Section 2, we present some preliminaries and lemmas that are to be used later to prove our main results. In Section 3, we discuss the controllability results for system (1.1). At last, an example is provided to illustrate the theory in Section 4. Section 5 is a conclusion.
2 Preliminaries and lemmas
For the convenience of the readers, we shall recall here some necessary definitions from fractional calculus theory and some properties of the measure of noncompactness, one can refer to the monographs by Podlubny [15], Miller and Ross [16] and Deimling [17].
In this paper, we denote by 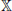 a Banach space with the norm . Assume that
a Banach space with the norm . Assume that  is another Banach space, denotes the space of bounded linear operators from
is another Banach space, denotes the space of bounded linear operators from 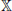 to
to  . We also use to denote the norm of f whenever , . Let denote the Banach space of functions which are Bochner integrable normed by . represents a Banach space endowed with supnorm, i.e., for .
. We also use to denote the norm of f whenever , . Let denote the Banach space of functions which are Bochner integrable normed by . represents a Banach space endowed with supnorm, i.e., for .
Definition 2.1 The fractional integral of order with the lower limit zero for a function is defined as
where is the Euler gamma function.
Definition 2.2 The Caputo fractional derivative of order with the lower limit zero for a functional x is defined as
where the function has absolutely continuous derivatives up to order .
Definition 2.3 (see [13])
A functional is said to be a mild solution of system (1.1) if it satisfies
where operators and are defined by
where
is the functional of Wright type defined on which satisfies
Lemma 2.1 (see [14])
The operators , () have the following properties:
-
(1)
For any fixed
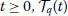 and
and 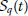 are linear bounded operators, i.e., for any
are linear bounded operators, i.e., for any 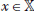
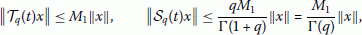 (2.3)
(2.3)where M1 is a positive constant to be specified later.
-
(2)
The operators () and () are strongly continuous. Therefore, for all and , one has
(2.4)
Lemma 2.2 Let 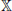 be a Banach space and the bounded set of
be a Banach space and the bounded set of 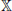 . The Kuratowski measure of noncompactness is the map defined by
. The Kuratowski measure of noncompactness is the map defined by
Lemma 2.3 Let , be two bounded sets of a Banach space 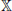 . Then:
. Then:
-
(1)
if and only if is relatively compact.
-
(2)
if .
-
(3)
.
Lemma 2.4 (see [18])
Let 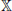 be a Banach space and be bounded and equicontinuous. Then is continuous on I, and
be a Banach space and be bounded and equicontinuous. Then is continuous on I, and
Lemma 2.5 (see [19])
Let 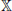 be a Banach space, let be a bounded and countable set. Then is Lebesgue integral on I, and
be a Banach space, let be a bounded and countable set. Then is Lebesgue integral on I, and
Lemma 2.6 (see [14])
Let 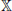 be a Banach space, be bounded. Then there exists a countable such that .
be a Banach space, be bounded. Then there exists a countable such that .
Lemma 2.7 (Fixed point theorem with respect to a convex-power condensing operator, see [20])
Let 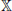 be a Banach space, let be bounded, closed and convex. Suppose that is a continuous operator and is bounded. For any and , set
be a Banach space, let be bounded, closed and convex. Suppose that is a continuous operator and is bounded. For any and , set
If there exist and a positive integer such that for any bounded and noncompact subset ,
then Q has at least one fixed point in D.
Definition 2.4 The fractional system (1.1) is said to be controllable on the interval I if, for every , there exists a control such that a mild solution x of system (1.1) satisfies .
3 Main results
For the convenience of presentation, we list here the following hypotheses to be used later.
-
(H1) The operator is a closed linear operator, and −A generates an equicontinuous -semigroup of uniformly bounded operators in
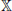 , there exists a constant such that .
, there exists a constant such that . -
(H2) The nonlinearity satisfies the Carathéodory type conditions, that is, is strong measure for all , and is continuous for a.e. .
-
(H3) For , there exist constants and functions such that for a.e. and all satisfying ,
Moreover, there exists a constant such that
-
(H4) There exist constants () such that for any bounded and countable sets () and a.e. ,
-
(H5) The nonlocal term is compact and continuous, there exist a constant and a nondecreasing continuous function such that, for some and all ,
-
(H6) The linear operator is bounded, defined by
has an inverse operator which takes values in , and there exist two positive constants such that
Theorem 3.1 Assume that hypotheses (H1)-(H6) are satisfied. Further assume that the following inequality holds:
then the fractional evolution system (1.1) is controllable on I.
Proof Define the operator as follows:
We shall show that, using the control
the operator Q has a fixed point, which is a mild solution of fractional evolution system (1.1). Note that and Definition 2.4, which means that system (1.1) is controllable on I.
Step 1. Q maps bounded sets into bounded sets.
For any , it follows from Lemma 2.1, hypotheses (H3), (H5) and (H6), and the Hölder inequality that
By (3.1) and (3.4), we know that . Therefore, Q maps bounded sets into bounded sets.
Step 2. Q is continuous in .
Assume that and . By hypotheses (H2) and (H5), we get
From hypothesis (H3), we have
Then by the Lebesgue dominated convergence theorem, we obtain that
Therefore, as , that is, Q is continuous.
Step 3. is equicontinuous.
For any and , we know that
Next, we shall show that as . For , by Lemma 2.1, as . For , by hypothesis (H3) and the Hölder inequality, we know that
Obviously, as . For , we have
So we get that as . For , , we have . For and small enough, by hypothesis (H3), the Lebesgue dominated convergence theorem, and the equicontinuity of , we get that
Then as , . In a similar way, for , , , , we obtain
It can be easily seen that , and tend to 0. Therefore, for any , as , which means that is equicontinuous.
Step 4. is a convex-power condensing operator.
Let , where means the closure of convex hull. It is easy to see that Q maps F into itself and is equicontinuous. Next, we shall show that there exists a positive integer such that for any bounded and nonprecompact subset , ,
Obviously, is also equicontinuous for and . Therefore, from Lemma 2.4, we attain
Note that by Lemma 2.6, there exists a countable set such that
By (H4) and (H6), we have
Suppose instead
then
There exists a countable set such that
where is the beta function. Suppose instead
Similarly, we get that
Then by the principle of mathematical induction, for any , we attain
So we have
From [14], there exists a large enough positive integer such that
Hence
Therefore is a convex-power condensing operator, Q has at least one fixed point, which is a mild solution of system (1.1). By Definition 2.4, system (1.1) is controllable on I. □
In order to obtain more controllability results, we replace conditions (H3) and (H5) by the following hypotheses:
() There exist a function , and a nondecreasing continuous function such that
for all and a.e. .
() The nonlocal term is compact and continuous, and there exist constants such that
Theorem 3.2 Assume that hypotheses (H1)-(H2), (), (H4) and () are satisfied. Further assume that there exists a constant R and the following inequality holds:
then the fractional evolution system (1.1) is controllable on I.
Proof By the definition of and the hypotheses we imposed, we have
From (3.26) we have
Using a similar method as in the previous proof, we can get that the fractional evolution system (1.1) is controllable on I. □
4 An example
Example 4.1 Consider the following fractional control system governed by a fractional partial differential equation:
where is a Caputo fractional partial derivative of order , F is a given function.
is continuous. Let , assume that the operator A is defined by , with the domain . It is well known that A is the infinitesimal generator of a differentiable (equicontinuity) semigroup () but not compact in 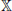 , which is given by
, which is given by
where (, ). Moreover, it is easy to get that
Put , , define the operator by , . Then, with the appropriate choice of A, B, f and g, the fractional evolution system (4.1) can be written in the form of (1.1). The following conditions hold:
has a bounded invertible operator defined by . If we can verify that all the conditions of Theorem 3.1 and inequality (3.1) are satisfied, the fractional control system (1.1) is controllable on , then the fractional control system (4.1) is controllable.
5 Conclusions
In this paper, using the uniform boundedness, equicontinuity of an operator semigroup and a fixed theorem with respect to a convex-power condensing operator, we have obtained the controllability of abstract fractional evolution control systems in a Banach space. It is well known that the compactness conditions of the operator semigroup can be weakened to equicontinuity. However, we have not only implemented a concrete assumption on the compactness condition via a parameter estimator but also removed the estimated parameter constraints; the sufficient conditions of controllability for various semilinear evolution systems are hence weakened. The conclusion of this paper is one of the most important developments in the aspect of imposing the necessary condition of controllability.
References
Yan Z: Controllability of fractional order partial neutral functional integrodifferential inclusions with infinite delay. J. Franklin Inst. 2011, 348: 2156–2173. 10.1016/j.jfranklin.2011.06.009
Balachandran K, Park JY: Controllability of fractional integrodifferential systems in Banach spaces. Nonlinear Anal. Hybrid Syst. 2009, 3: 363–367. 10.1016/j.nahs.2009.01.014
Chang YK, Chalishajar DN: Controllability of mixed Volterra-Fredholm type integro-differential inclusions in Banach spaces. J. Franklin Inst. 2008, 345: 499–507. 10.1016/j.jfranklin.2008.02.002
Chalishajar DN: Controllability of mixed Volterra-Fredholm type integrodifferential systems in Banach space. J. Franklin Inst. 2007, 344: 12–21. 10.1016/j.jfranklin.2006.04.002
Hernández EM, O’Regan D: Controllability of Volterra-Fredholm type systems in Banach spaces. J. Franklin Inst. 2009, 346: 95–101. 10.1016/j.jfranklin.2008.08.001
Wang F, Liu Z, Li J: Complete controllability of fractional neutral differential systems in abstract space. Abstr. Appl. Anal. 2013., 2013: Article ID 529025
Fec̆kan M, Wang J, Zhou Y: Controllability of fractional functional evolution equations of Sobolev type via characteristic solution operators. J. Optim. Theory Appl. 2013, 156: 79–95. 10.1007/s10957-012-0174-7
Ji S, Li G, Wang M: Controllability of impulsive differential systems with nonlocal conditions. Appl. Math. Comput. 2011, 217: 6981–6989. 10.1016/j.amc.2011.01.107
Machado JA, Ravichandran C, Rivero M, Trujillo JJ: Controllability results for impulsive mixed type functional integrodifferential evolution equations with nonlocal conditions. Fixed Point Theory Appl. 2013., 2013: Article ID 66
Zhu L, Huang Q, Li G: Abstract semilinear evolution equations with convex power condensing operators. J. Funct. Spaces Appl. 2013., 2013: Article ID 473876
Xue X: Nonlocal nonlinear differential equations with a measure of noncompactness in Banach spaces. Nonlinear Anal. 2009, 70: 2593–2601. 10.1016/j.na.2008.03.046
Ahmad B, Malar K, Karthikeyan K: A study of nonlocal problems of impulsive integrodifferential equations with measure of noncompactness. Adv. Differ. Equ. 2013., 2013: Article ID 205
Wang J, Zhou Y: Complete controllability of fractional evolution systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 4346–4355. 10.1016/j.cnsns.2012.02.029
Chen P, Li Y: Nonlocal problem for fractional evolution equations of mixed type with the measure of noncompactness. Abstr. Appl. Anal. 2013., 2013: Article ID 784816
Podlubny I: Fractional Differential Equations. Academic Press, San Diego; 1999.
Miller KS, Ross B: An Introduction to Fractional Calculus and Differential Equations. Wiley, New York; 1993.
Deimling K: Nonlinear Functional Analysis. Springer, New York; 1985.
Banaś J, Goebel K Lecture Notes in Pure and Applied Mathematics 60. In Measures of Noncompactness in Banach Spaces. Dekker, New York; 1980.
Heinz HP: On the behaviour of measure of noncompactness with respect to differentiation and integration of vector valued functions. Nonlinear Anal., Theory Methods Appl. 1983,7(12):1351–1371. 10.1016/0362-546X(83)90006-8
Sun J, Zhang X: The fixed point theorem of convex-power condensing evolution equations. Acta Math. Sin. 2005,48(3):439–446. (in Chinese)
Acknowledgements
The authors thank the anonymous referees and handing editor of the manuscript for their valuable suggestions and fruitful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have contributed to this work on an equal basis. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qin, H., Liu, J. & Zuo, X. Controllability problem for fractional integrodifferential evolution systems of mixed type with the measure of noncompactness. J Inequal Appl 2014, 292 (2014). https://doi.org/10.1186/1029-242X-2014-292
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2014-292
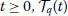 and
and 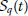 are linear bounded operators, i.e., for any
are linear bounded operators, i.e., for any