Bilinear Calderón-Zygmund operators of type $\mathrm{\omega }(t)$ on non-homogeneous space

Abstract

Let $(\mathcal{X},d,\mu )$ be a geometrically doubling metric spaces and the measure μ satisfy the upper doubling condition. The aim of this paper, under this assumption, is to study the boundedness of the bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$. As an application, we obtain the Morrey boundedness properties of the bilinear operator.

MSC:42B20, 42B25, 42B35.

1 Introduction and main results

In the last few decades, the classical theory of the singular integral has played an important role in harmonic analysis. One of the main features of these works is that the underlying spaces or domains 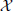possess the measure doubling property,

$$\mu (Q(x,2r))\le C\mu (Q(x,r)),$$

(1.1)

where μ is a Borel measure, $Q(x,r)$ denotes the ball with center x and radius $r>0$. A metric space $(\mathcal{X},d)$ equipped with such a measure μ is called a space of homogeneous type. It is well known that the measure doubling condition in the analysis on spaces of homogeneous type is a key assumption, such as that Euclidean spaces with weighted measures satisfy the doubling property (1.1).

However, recently, some works indicated that the measure doubling condition is superfluous for most of the classical singular integral operator theory, and many results on the Calderón-Zygmund theory have been proved valid if the condition (1.1) is replaced by a mild volume growth condition,

$$\mu (Q(x,r))\le C_0{r}^d,$$

(1.2)

where $C_0$ is a positive constant, d is a dimension of the underlying spaces, $x\in \mathcal{X}$, $r\in (0,\mathrm{\infty })$. Such a measure does not satisfy the doubling condition. For example, Tolsa [1] established Calderón-Zygmund theory for a nondoubling measure and introduced the RBMO spaces, a variant of the space BMO, and he proved that Calderón-Zygmund operators are bounded from $H^1(\mu )$ into $L^1(\mu )$. Nazarov et al. [2] showed that if T is a Calderón-Zygmund operator bounded on $L^2(\mu )$, then T is bounded on $L^p(\mu )$ for all $p\in (1,\mathrm{\infty })$ and from $L^1(\mu )$ into $L^{1,\mathrm{\infty }}(\mu )$.

Recently, Hytönen [3] gave a new class of metric measures spaces $(\mathcal{X},d,\mu )$ (instead of $({\mathbb{R}}^n,d,\mu )$), which are called non-homogeneous spaces, the measure μ satisfies the upper doubling condition (see definition 1.3). The new class of metric measures spaces are sufficiently general to include in a natural way both the space of homogeneous type and a metric space with the mild volume growth condition.

Anh and Doung [4] established the boundedness of Calderón-Zygmund operator on various function spaces on $(\mathcal{X},d,\mu )$ and they extended the work of Tolsa on the non-homogeneous spaces $({\mathbb{R}}^n,d,\mu )$ to a more general non-homogeneous spaces $(\mathcal{X},d,\mu )$.

Meanwhile, multilinear Calderón-Zygmund theory has been studied by many researchers. The theory was introduced by Coifman and Meyer [5] in 1975 and it was further investigated by Grafakos and Torres [6]. Chen and Fan [7, 8] obtained some estimates for the bilinear singular integral. Xu [9] obtained the boundedness of a multilinear Calderón-Zygmund operator on $L^p({\mathbb{R}}^n,\mu )$, $1<p<\mathrm{\infty }$.

Yabuta [10] introduced a generalized operator: a Calderón-Zygmund operator of type $\mathrm{\omega }(t)$, which generalizes the classical Calderón-Zygmund operator. Maldonado and Naibo [11] developed a theory of the bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ (see Definition 1.4) and extended some results of Yabuta.

Theorem A [11]

Consider $\mathrm{\omega }(t)\in Dini(1/2)$, and let T be a bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ in ${\mathbb{R}}^n$. If $1<p_1,p_2<\mathrm{\infty }$ and $\frac{1}{2}\le p<\mathrm{\infty }$ such that $\frac{1}{p}=\frac{1}{p_1}+\frac{1}{p_2}$, then T can be extended to a bounded operator from $L^{p_1}({\mathbb{R}}^n)\times L^{p_2}({\mathbb{R}}^n)$ into $L^p({\mathbb{R}}^n)$, where $L^{p_1}({\mathbb{R}}^n)$ or $L^{p_2}({\mathbb{R}}^n)$ should be replaced by $L_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ if $p_1=\mathrm{\infty }$ or $p_2=\mathrm{\infty }$, respectively.

In this paper, we study the boundedness of a bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ on a non-homogeneous metric space, where we only assume $\mathrm{\omega }\in Dini(1)$. And we also note that the condition of kernel (1.5) is more general than the size condition defined by Hu [12]. So this is a new result, which generalizes some works of Maldonado and Naibo [11] and Anh and Doung [4] on $(\mathcal{X},d,\mu )$. As an application, we investigate the boundedness of the bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ over a Morrey space on $(\mathcal{X},d,\mu )$.

Before stating our main results, we fix some notations and define some terminologies. Throughout this paper, a ball Q denotes $Q=Q(x,r)=\{y\in \mathcal{X}:d(x,y)<r\}$ which is equipped with a fixed center $x\in \mathcal{X}$ and radius $r>0$. The center and radius of Q are denoted by $x_Q$ and $r_Q$. For $\alpha >0$ and $Q=Q(x,r)$, the notation $\alpha Q:=Q(x,\alpha Q)$ stands for the concentric dilation of Q. For notational convenience, we will occasionally write $\overrightarrow{f}=(f_1,f_2)$. The following notions of geometrically doubling and upper doubling measures μ are originally from Hytönen [3].

We finally observe that in the sequel the letter C will be used to denote various constants which do not depend on the functions.

Definition 1.1 A metric space $(\mathcal{X},d)$ is called geometrically doubling if there exists a number $N\in \mathbb{N}$ such that any open ball $Q(x,r)\subset \mathcal{X}$ can be covered by at most N balls $Q(x_i,\frac{r}{2})$.

Lemma 1.2 For a metric space $(\mathcal{X},d)$, the following statements are equivalent:

• (1) $(\mathcal{X},d)$ is geometrically doubling.

• (2) For any $ϵ\in (0,1)$, any ball $Q(x,r)\subset \mathcal{X}$ can be covered by at most $N{ϵ}^{-n}$ balls $Q(x_i,ϵr)$.

• (3) For every $ϵ\in (0,1)$, any ball $Q(x,r)\subset \mathcal{X}$ can contain at most $N{ϵ}^{-n}$ centers $x_i$ of disjoint balls $Q(x_i,ϵr)$.

• (4) There exists $M\in \mathbb{N}$ such that any ball $Q(x,r)\subset \mathcal{X}$ can contain at most M centers $x_i$ of disjoint balls ${\{Q(x_i,r/4)\}}_{i=1}^M$.

Definition 1.3 A Borel measure μ in the metric space $(\mathcal{X},d,\mu )$ is said to be an upper doubling measures if there exists a dominating function $\lambda :\mathcal{X}\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ and a constant $C_{\lambda }$ such that:

• (1) For any fixed $x\in \mathcal{X}$, $r\mapsto \lambda (x,r)$ is increasing.

• (2) $\lambda (x,2r)\le C_{\lambda }\lambda (x,r)$.

• (3) The inequality $\mu (x,r):=\mu (Q(x,r))\le \lambda (x,r)\le C_{\lambda }\lambda (x,r/2)$ holds for all $x\in \mathcal{X}$, $0<r<\mathrm{\infty }$.

• (4) $\lambda (x,r)\approx \lambda (y,r)$ for all $r>0$, $x,y\in \mathcal{X}$ and $d(x,y)\le r$.

Remark 1 If we take the dominating function $\lambda (x,r)$ to be $\mu (Q(x,r))$, then the measure doubling is a special case of upper doubling. On the other hand, a Radon measure μ as in (1.2) on ${\mathbb{R}}^d$ is also an upper doubling measure by taking the dominating function $\lambda (x,r)=C_0{r}^d$.

In this paper, we assume that $(\mathcal{X},d,\mu )$ is a geometrically doubling metric spaces and the measure μ is an upper doubling measure. And we denote $L^p(\mathcal{X},\mu )$ by $L^p(\mu )$ for brevity.

We recall the Calderón-Zygmund operator defined by Anh and Doung [4]. A kernel $K(\cdot ,\cdot )\in L_{\mathrm{loc}}^1(\mathcal{X}\times \mathcal{X}\setminus \{(x,y):x=y\})$ is called a Calderón-Zygmund kernel if it satisfies

$$|K(x,y)|\le min\{\frac{1}{\lambda (x,d(x,y))},\frac{1}{\lambda (y,d(x,y))}\}$$

(1.3)

for all $(x,y)\in \mathcal{X}\times \mathcal{X}$ with $x\ne y$. There exists $0<\delta \le 1$ such that

$$|K(x,y)-K(x^{\prime },y)|+|K(y,x)-K(y,x^{\prime })|\le \frac{d{(x,x^{\prime })}^{\delta }}{d{(x,y^{\prime })}^{\delta }\lambda (x,d(x,y))}.$$

(1.4)

A linear operator T is called a Calderón-Zygmund operator with $K(\cdot ,\cdot )$ satisfying the above conditions if for all $f\in L^{\mathrm{\infty }}(\mu )$ with bounded support and $x\notin suppf$,

$$Tf(x)={\int }_{\mathcal{X}}k(x,y)f(y)d\mu (y).$$

A new example of operators with kernel satisfying (1.3) and (1.4) is called Bergman-type operator; it appeared in [13].

For $a>0$, we write $\mathrm{\omega }\in Dini(a)$ if $\mathrm{\omega }:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$, ω is nondecreasing, concave, and

$${|\mathrm{\omega }|}_{Dini(a)}:={\int }_0^1{\mathrm{\omega }}^a(t)\frac{dt}{t}<\mathrm{\infty }.$$

Now we define bilinear Calderón-Zygmund kernel of type $\mathrm{\omega }(t)$ and the corresponding bilinear Calderón-Zygmund operators.

Denote

$$\frac{1}{{[\lambda (x,d(x,\tilde{y}))]}^2}=\underset{i\in \{1,2\}}{min}\left\{\frac{1}{{(\lambda (x,d(x,y_i)))}^2}\right\}.$$

Definition 1.4 Let $\mathrm{\omega }:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ be a nondecreasing function and $K(x,y_1,y_2)$ be a locally integrable function defined away from the diagonal $x=y_1=y_2$ in ${(\mathcal{X})}^3$. We say that $K(x,y_1,y_2)$ is a bilinear Calderón-Zygmund kernel of type $\mathrm{\omega }(t)$ if it satisfies the size condition,

$$|K(x,y_1,y_2)|\le C_K\frac{1}{{[\lambda (x,d(x,\tilde{y}))]}^2}$$

(1.5)

for some $C_K>0$ and all $(x,y_1,y_2)\in {(\mathcal{X})}^3$ with $x\ne y_i$ for some i. We have the smoothness estimates,

$$\begin{array}{r}|K(x+h,y_1,y_2)-K(x,y_1,y_2)|+|K(x,y_1+h,y_2)-K(x,y_1,y_2)|\\ +|K(x,y_1,y_2+h)-K(x,y_1,y_2)|\\ \le C_K\frac{1}{{[\lambda (x,d(x,\tilde{y}))]}^2}\mathrm{\omega }\left(\frac{|h|}{{\sum }_{i=1}^{2}d(x,y_i)}\right),\end{array}$$

(1.6)

whenever $|h|\le \frac{1}{2}{max}_{i\in \{1,2\}}d(x,y_i)$.

A bilinear operator $T_{\mathrm{\omega }}:\mathcal{S}\times \mathcal{S}\to {\mathcal{S}}^{\prime }$ is said to be associated with a bilinear Calderón-Zygmund kernel of type $\mathrm{\omega }(t)$, if

$$T_{\mathrm{\omega }}(f_1,f_2)(x)={\int }_{\mathcal{X}}{\int }_{\mathcal{X}}K(x,y_1,y_2)f_1(y_1)f_2(y_2)d\mu (y_1)d\mu (y_2)$$

(1.7)

for all $f_i\in C_0^{\mathrm{\infty }}$, and $x\notin {\bigcap }_{i=1}^{2}supp{f}_i$.

If the bilinear operator $T_{\mathrm{\omega }}$ is associated with $K(x,y_1,y_2)$ and admits some bounded extensions

$$T_{\mathrm{\omega }}:L^{r_1}(\mu )\times L^{r_2}(\mu )\to L^{r,\mathrm{\infty }}(\mu )$$

for some $1<r_i<\mathrm{\infty }$ ($i=1,2$) and $r>1$ with ${\sum }_{i=1}^2\frac{1}{r_i}=\frac{1}{r}$, or

$$T_{\mathrm{\omega }}:L^{r_1}(\mu )\times L^{r_2}(\mu )\to L^1(\mu )$$

for some $1<r_i<\mathrm{\infty }$ ($i=1,2$) and ${\sum }_{i=1}^2\frac{1}{r_i}=1$, then $T_{\mathrm{\omega }}$ is said to be a bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$.

Note that $\lambda (x,r)\approx \lambda (y,r)$ for all $r>0$, $x,y\in \mathcal{X}$ and $d(x,y)\le r$. When $\mathrm{\omega }(t)=t^{\delta }$, $\delta \in (0,1]$, the linear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ is the Calderón-Zygmund operator defined by Anh and Doung [4], so our results are more general.

Theorem 1.5 Consider $\mathrm{\omega }\in Dini(1)$, and let $T_{\mathrm{\omega }}$ be a bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ with $K(x,y_1,y_2)$. Assume $1<p,p_1,p_2<\mathrm{\infty }$, ${\sum }_{i=1}^2\frac{1}{p_i}=\frac{1}{p}$ and $f_i\in L^{p_i}(\mu )$ with ${\int }_{{\mathbb{R}}^d}{T}_{\mathrm{\omega }}(f_1,f_2)(x)d\mu (x)=0$ if $\parallel \mu \parallel <\mathrm{\infty }$. Suppose $T_{\mathrm{\omega }}$ is a bounded operator from $L^1(\mu )\times L^1(\mu )\to L^{1/2,\mathrm{\infty }}(\mu )$, then there exists a constant C such that

$${\parallel T_{\mathrm{\omega }}(f_1,f_2)\parallel }_{L^p(\mu )}\le C\prod _{i=1}^2{\parallel f_i\parallel }_{L^{p_i}(\mu )},$$

the constant C depends only on $C_K$, $p_i$, p.

Remark 2 The assumption of ω in [11] is $\mathrm{\omega }\in Dini(1/2)$, which is stronger than $\mathrm{\omega }\in Dini(1)$, and it is easy to see because $\mathrm{\omega }(t)$ is nondecreasing,

$${\int }_0^1\mathrm{\omega }(t)\frac{dt}{t}={\int }_0^1{\mathrm{\omega }}^{\frac{1}{2}}(t){\mathrm{\omega }}^{\frac{1}{2}}(t)\frac{dt}{t}\le {\mathrm{\omega }}^{\frac{1}{2}}(1){\int }_0^1{\mathrm{\omega }}^{\frac{1}{2}}(t)\frac{dt}{t}.$$

Next, we give the boundedness of the bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$ over Morrey space on $(\mathcal{X},d,\mu )$ (for the Morrey space see Definition 3.1).

Theorem 1.6 Assume that $T_{\mathrm{\omega }}$ is a bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$, let $p_i\in (1,\mathrm{\infty })$ and $f_i\in L^{p_i}(\mu )$ for $i=1,2$. Suppose $T_{\mathrm{\omega }}$ is a bounded operator from $L^1(\mu )\times L^1(\mu )$ to $L^{1/2,\mathrm{\infty }}(\mu )$, then there exists a constant C such that

$${\parallel T_{\mathrm{\omega }}(f_1,f_2)\parallel }_{M_q^p(\mu )}\le C\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )},$$

where $1<q_i\le p_i$ and ${\sum }_{i=1}^2\frac{1}{p_i}=\frac{1}{p}$, ${\sum }_{i=1}^2\frac{1}{q_i}=\frac{1}{q}$.

2 Proof of the result

Before we prove Theorem 1.5, we need some notations and lemmas.

Definition 2.1 For any two balls $Q\subset R$, we define

$$K_{Q,R}=1+{\int }_{r_Q\le d(x,x_Q)\le r_R}\frac{1}{\lambda (x_Q,d(x,x_Q))}d\mu (x).$$

(2.1)

For $\alpha ,\beta >1$, a ball $Q\subset \mathcal{X}$ is said to be $(\alpha ,\beta )$-doubling if $\mu (\alpha Q)\le \beta \mu (Q)$.

Lemma 2.2 [4]

• (1) If $Q\subset R\subset S$ are balls in 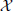, then

  $$max\{K_{Q,R},K_{R,S}\}\le K_{Q,S}\le \{K_{Q,R}+K_{R,S}\}.$$

• (2) If $Q\subset R$ are of compatible size, then $K_{Q,R}\le C$.

• (3) If $\alpha Q,\dots ,{\alpha }^{N-1}Q$ are non-$(\alpha ,\beta )$-doubling balls ($\beta >C_{\lambda }^{{log}_2\alpha }$), then $K_{Q,{\alpha }^{N}Q}\le C$.

In what follows, unless α, β are specified otherwise, by a doubling ball we mean a $(6,{\beta }_0)$-doubling with a fixed number ${\beta }_0>max\{C_{\lambda }^{3{log}_2^6},6^{3n}\}$, where n can be viewed as a geometric dimension of the spaces.

For any fixed ball $Q\subset \mathcal{X}$, let $N\ge 0$ be the smallest integer such that $6^{N}Q$ is doubling, we denote this ball by $\tilde{Q}$. Denote by $m_{Q}f$ the mean value of f on Q, namely, $m_{Q}f=\frac{1}{\mu (Q)}{\int }_{Q}f(x)d\mu$. Let $\eta >1$ be a fixed constant, we say that $f\in L_{\mathrm{loc}}^1(\mu )$ is in $RBMO(\mu )$ if there exists a constant such that

$$\frac{1}{\mu (\eta Q)}{\int }_Q|f(y)-m_{\tilde{Q}}f|d\mu (y)\le \mathcal{A}$$

(2.2)

for any ball Q, and

$$|m_{Q}f-m_{R}f|\le \mathcal{A}{K}_{Q,R}$$

(2.3)

for any two doubling balls $Q\subset R$. The minimal constant is the $RBMO(\mu )$ norm of f, and it will be denoted by ${\parallel f\parallel }_{\ast }$.

We will prove Theorem 1.5 via the boundedness of sharp maximal estimates. Let f be a function in $L_{\mathrm{loc}}^1(\mu )$, the sharp maximal function of f is defined by

$$M^{\mathrm{♯}}f(x)=\underset{Q\ni x}{sup}\frac{1}{\mu (30Q)}{\int }_Q|f(y)-m_{\tilde{Q}}f|d\mu (y)+\underset{Q,R\mathrm{doubling}}{\underset{R\supset Q\ni x}{sup}}\frac{|m_{Q}f-m_{R}f|}{K_{Q,R}},$$

(2.4)

where the supremum is taking over all the balls Q containing the point x. In order to prove our results, we need a variant of (2.4)

$$M_{\delta }^{\mathrm{♯}}f(x)={(M^{\mathrm{♯}}{|f|}^{\delta }(x))}^{\frac{1}{\delta }}.$$

For $k\ge 5$, we denote the non-centered Hardy-Littlewood maximal operator

$$M_{(k)}f(x)=\underset{x\in Q\subset \mathcal{X}}{sup}\frac{1}{\mu (kQ)}{\int }_Q|f(y)|d\mu (y),$$

which is bounded on $L^p(\mathcal{X},\mu )$ for $p>1$, we can find the proof in [3]. We also need the following multilinear maximal operator:

$${\mathcal{M}}_{(k)}(\overrightarrow{f})(x)=\underset{x\in Q\subset \mathcal{X}}{sup}\prod _{i=1}^2\frac{1}{\mu (kQ)}{\int }_Q|f_i(y_i)|d\mu (y_i),k\ge 5,$$

which is introduced by Lerner [14] when μ is Lebesgue measure and $k=1$. It obvious that the operator ${\mathcal{M}}_k(\overrightarrow{f})$ is strictly controlled by the 2-fold product of $M_{(k)}f$.

The non-centered doubling maximal operator is defined by

$$Nf(x)=\underset{Q\mathrm{doubling}}{\underset{Q\ni x}{sup}}\frac{1}{\mu (Q)}{\int }_Q|f(y)|d\mu (y),$$

(2.5)

we denote $N_{\delta }f(x)={(N{|f|}^{\delta }(x))}^{\frac{1}{\delta }}$. By the Lebesgue differential theorem, it is easy to see that $|f(x)|\le N_{\delta }f(x)$ for any $f\in L_{\mathrm{loc}}^1(\mu )$ and μ-a.e. $x\in \mathcal{X}$.

Lemma 2.3 Let $f\in L_{\mathrm{loc}}^1(\mu )$ with the extra condition $\int fd\mu =0$ if $\parallel \mu \parallel :=\mu (\mathcal{X})<\mathrm{\infty }$. Assume that for some p, $1<p<\mathrm{\infty }$, $inf\{1,Nf\}\in L^p(\mathcal{X},\mu )$. Then we have

$${\parallel N_{\delta }f\parallel }_{L^p(\mu )}\le C{\parallel {\mathcal{M}}_{\delta }^{\mathrm{♯}}f\parallel }_{L^p(\mu )}.$$

The proof of Lemma 2.3 needs a slight modification of the proof of Theorem 4.2 in [4], so we omit the details.

In the following proofs we will employ several times the following simple Kolmogorov inequality. Let $(\mathcal{X},d,\mu )$ be a probability measure spaces and let $0<p<q<\mathrm{\infty }$, then there is a constant $C=C_{p,q}$ such that for any measurable function f,

$${\parallel f\parallel }_{L^p(\mu )}\le C{\parallel f\parallel }_{L^{q,\mathrm{\infty }}(\mu )}.$$

(2.6)

Lemma 2.4 Let $T_{\mathrm{\omega }}$ be a bilinear Calderón-Zygmund operator of type $\mathrm{\omega }(t)$, $0<\delta <\frac{1}{2}$. Suppose $T_{\mathrm{\omega }}$ is bounded from $L^1(\mu )\times L^1(\mu )$ to $L^{1/2,\mathrm{\infty }}(\mu )$, then there exists a constant C such that

$$M_{\delta }^{\mathrm{♯}}(T_{\mathrm{\omega }}(\overrightarrow{f}))(x)\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x),$$

(2.7)

for any $f_i\in L_c^{\mathrm{\infty }}(\mu )$ and for every $x\in \mathcal{X}$.

Proof In order to prove (2.7), we combine the techniques of Theorem 3.2 in [14] with the methods of Theorem 9.1 in [1], so it suffices to prove that

$${(\frac{1}{\mu (30Q)}{\int }_Q{|T_{\mathrm{\omega }}(\overrightarrow{f})(y)-h_Q|}^{\delta }d\mu (y))}^{\frac{1}{\delta }}\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x)$$

(2.8)

and

$$|h_Q-h_R|\le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x)$$

(2.9)

hold for any balls $Q\subset R$ with $x\in Q$, Q is an arbitrary ball,

$$\begin{array}{c}{h}_Q=m_Q(T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})+T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)+T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})),\hfill \\ h_R=m_R(T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})+T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)+T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})),\hfill \end{array}$$

where we split each $f_i$ as $f_i=f_i^0+f_i^{\mathrm{\infty }}$, $f_i^0=f_i{\chi }_{6Q}$ and $f_i^{\mathrm{\infty }}=f_i-f_i^0$, and we have

$$\begin{array}{rl}|T_{\mathrm{\omega }}(\overrightarrow{f})(y)|=& |T_{\mathrm{\omega }}(f_1,f_2)(y)|\\ \le & |T_{\mathrm{\omega }}(f_1^0,f_2^0)(y)|+|T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(y)|\\ +|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(y)|+|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y)|.\end{array}$$

So we obtain

$$\begin{array}{r}\frac{1}{\mu (30Q)}{\int }_Q{|T_{\mathrm{\omega }}(\overrightarrow{f})(y)-h_Q|}^{\delta }d\mu (y)\\ \le \frac{1}{\mu (30Q)}{\int }_Q{|T_{\mathrm{\omega }}(f_1^0,f_2^0)(y)|}^{\delta }d\mu (y)\\ +\frac{1}{\mu (30Q)}\frac{1}{\mu (Q)}{\int }_Q{\int }_Q|[T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(y)-T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(z)]\\ +[T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(y)-T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(z)]{|}^{\delta }d\mu (z)d\mu (y)\\ +\frac{1}{\mu (30Q)}\frac{1}{\mu (Q)}{\int }_Q{\int }_Q|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y)-T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(z){|}^{\delta }d\mu (z)d\mu (y)\\ :=I+II+III.\end{array}$$

For the first term I, applying Kolmogorov’s inequality (2.6) with $p=\delta$ and $q=1/2$, we derive

$$\begin{array}{rl}{I}^{\frac{1}{\delta }}& ={(\frac{1}{\mu (30Q)}{\int }_Q{|T_{\mathrm{\omega }}(f_1^0,f_2^0)(y)|}^{\delta }d\mu (y))}^{\frac{1}{\delta }}\\ \le C_{\delta }{\left(\frac{\mu (Q)}{\mu (30Q)}\right)}^{\frac{1}{\delta }}{\parallel T_{\mathrm{\omega }}(f_1{\chi }_{6Q},f_2{\chi }_{6Q})\parallel }_{L^{1/m,\mathrm{\infty }}(Q,\frac{d\mu }{\mu (Q)})}\\ \le C_{\delta }{\left(\frac{\mu (Q)}{\mu (30Q)}\right)}^{\frac{1}{\delta }}\prod _{i=1}^2\frac{1}{\mu (Q)}{\int }_{6Q}|f_i(y_i)|d\mu (y_i)\\ \le C_{\delta }{\left(\frac{\mu (Q)}{\mu (30Q)}\right)}^{\frac{1}{\delta }}\prod _{i=1}^2\frac{\mu (5\times 6Q)}{\mu (Q)}\frac{1}{\mu (5\times 6Q)}{\int }_{6Q}|f_i(y_i)|d\mu (y_i)\\ \le C_{\delta }{\left(\frac{\mu (Q)}{\mu (30Q)}\right)}^{\frac{1}{\delta }-2}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x)\\ \le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x),\end{array}$$

since $T:L^1(\mu )\times L^1(\mu )\to L^{1/2,\mathrm{\infty }}(\mu )$.

Next we consider II. Firstly, the condition $d(y,z)\le \frac{1}{2}max\{d(y,y_1),d(y,y_2)\}$ holds since $y,z\in Q$, $y_1\in 6Q$, $y_2\in {(6Q)}^c$, then we have the following estimates:

$$\begin{array}{r}|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(y)-T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(z)|\\ \le C{\int }_{6Q}{\int }_{\mathcal{X}\setminus 6Q}\frac{1}{{[\lambda (y,d(y,\tilde{y}))]}^2}\mathrm{\omega }\left(\frac{d(z,y)}{{\sum }_{i=1}^{2}d(y,y_i)}\right)|f_1(y_1)||f_2(y_2)|d\mu (y_1)d\mu (y_2)\\ \le C{\int }_{6Q}|f_2(y_2)|{\int }_{\mathcal{X}\setminus 6Q}\frac{|f_1(y_1)|}{{[\lambda (y,d(y,y_1))]}^2}\mathrm{\omega }\left(\frac{d(z,y)}{d(y,y_1)}\right)d\mu (y_1)d\mu (y_2)\\ \le \frac{C}{\lambda (y,d(y,y_2))}{\int }_{6Q}|f_2(y_2)|\sum _{k=1}^{\mathrm{\infty }}{\int }_{6^{k+1}Q\setminus 6^{k}Q}\frac{1}{\lambda (y,d(y,y_1))}\mathrm{\omega }\left(\frac{d(z,y)}{d(y,y_1)}\right)d\mu (y_1)d\mu (y_2)\\ \le \frac{C}{\lambda (x_Q,6r_Q)}{\int }_{6Q}|f_2(y_2)|d\mu (y_2)\sum _{k=1}^{\mathrm{\infty }}\frac{1}{\lambda (x_Q,6^k{r}_Q)}{\int }_{6^{k+1}Q\setminus 6^{k}Q}|f_1(y_1)|d\mu (y_1)\mathrm{\omega }\left(6^{-k}\right)\\ \le C\frac{\mu (5\times 6Q)}{\lambda (x_Q,6r_Q)}\frac{1}{\mu (5\times 6Q)}{\int }_{6Q}|f_2(y_2)|d\mu (y_2)\\ \times \sum _{k=1}^{\mathrm{\infty }}\mathrm{\omega }\left(6^{-k}\right)\frac{\mu (5\times 6^{k+2}Q)}{\lambda (x_Q,6^k{r}_Q)}\frac{1}{\mu (5\times 6^{k+2}Q)}{\int }_{6^{k+2}Q}|f_1(y_1)|d\mu (y_1)\\ \le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x)\sum _{k=1}^{\mathrm{\infty }}\mathrm{\omega }\left(6^{-k}\right)\\ \le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}$$

Here the series ${\sum }_{k=1}^{\mathrm{\infty }}\mathrm{\omega }(6^{-k})$ is equivalent to ${\int }_0^1\mathrm{\omega }(t)\frac{dt}{t}$, where $\mathrm{\omega }\in Dini(1)$. We use the estimate, since $\lambda (x,2r)\le C_{\lambda }\lambda (x,r)$,

$$\frac{\mu (5\times 6Q)}{\lambda (x_Q,6r_Q)}\le \frac{\lambda (x_Q,5\times 6r_Q)}{\lambda (x_Q,6r_Q)}\le C_{\lambda }^{{log}_2^5+1},$$

and

$$\frac{\mu (5\times 6^{k+2}Q)}{\lambda (x_Q,6^k{r}_Q)}\le \frac{\lambda (x_Q,5\times 6^2\times 6^k{r}_Q)}{\lambda (x_Q,6^k{r}_Q)}\le C_{\lambda }^{6{log}_2^5+1}.$$

We will use the same methods several times.

Similarly, we have

$$|T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(y)-T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(z)|\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

By the estimates above, we have

$$I{I}^{\frac{1}{\delta }}\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

It remains to consider the term in $III$. For $y,z\in Q$, noting that $d(y,z)\le \frac{1}{2}max\{d(y,y_1),d(y,y_2)\}$ for $y_i\in {(6Q)}^c$ ($i=1,2$), we use the condition of kernel (1.6) to obtain

$$\begin{array}{r}|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y)-T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(z)|\\ \le C{\int }_{\mathcal{X}\setminus 6Q}{\int }_{\mathcal{X}\setminus 6Q}\frac{1}{{[\lambda (y,d(y,\tilde{y}))]}^2}\\ \times \mathrm{\omega }\left(\frac{d(z,y)}{{\sum }_{i=1}^{2}d(y,y_i)}\right)|f_1(y_1)||f_2(y_2)|d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=k}^{\mathrm{\infty }}{\int }_{6^{k+1}Q\setminus 6^{k}Q}|f_2(y_2)|{\int }_{6^{j+1}Q\setminus 6^{j}Q}\frac{|f_1(y_1)|}{{[\lambda (y,d(y,y_1))]}^2}\\ \times \mathrm{\omega }\left(\frac{d(y,z)}{d(y,y_1)}\right)d\mu (y_1)d\mu (y_2)\\ +C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=1}^{k-1}{\int }_{6^{k+1}Q\setminus 6^{k}Q}\frac{|f_2(y_2)|}{{[\lambda (y,d(y,y_2))]}^2}\mathrm{\omega }\left(\frac{d(y,z)}{d(y,y_2)}\right)\\ \times {\int }_{6^{j+1}Q\setminus 6^{j}Q}|f_1(y_1)|d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=k}^{\mathrm{\infty }}{\int }_{6^{k+1}Q\setminus 6^{k}Q}|f_2(y_2)|{\int }_{6^{j+1}Q\setminus 6^{j}Q}\frac{|f_1(y_1)|}{{[\lambda (y,d(y,y_1))]}^2}\\ \times \mathrm{\omega }\left(\frac{d(y,z)}{d(y,y_1)}\right)d\mu (y_1)d\mu (y_2)\\ +C\sum _{k=1}^{\mathrm{\infty }}{\int }_{6^{k+1}Q\setminus 6^{k}Q}\frac{|f_2(y_2)|}{{[\lambda (y,d(y,y_2))]}^2}\\ \times \mathrm{\omega }\left(\frac{d(y,z)}{d(y,y_2)}\right){\int }_{6^{k}Q\setminus 6Q}|f_1(y_1)|d\mu (y_1)d\mu (y_2)\\ :=II{I}_1+II{I}_2.\end{array}$$

A trivial computation now shows that

$$\begin{array}{rcl}II{I}_1& \le & C\sum _{j=1}^{\mathrm{\infty }}(\frac{1}{{[\lambda (x_Q,6^j{r}_Q)]}^2}{\int }_{6^{j+1}Q\setminus 6^{j}Q}|f_1(y_1)|d\mu (y_1)\mathrm{\omega }\left(\frac{r_Q}{6^j{r}_Q}\right))\\ \times \sum _{k=1}^j{\int }_{6^{k+1}Q\setminus 6^{k}Q}|f_2(y_2)|d\mu (y_2)\\ \le & C\sum _{j=1}^{\mathrm{\infty }}(C_{\lambda }^{{log}_2^{30}+1}\frac{1}{{[\lambda (x_Q,5\times 6^{j+1}{r}_Q)]}^2}{\int }_{6^{j+1}Q}|f_1(y_1)|d\mu (y_1))\mathrm{\omega }\left(\frac{r_Q}{6^j{r}_Q}\right)\\ \times {\int }_{6^{j+1}Q}|f_2(y_2)|d\mu (y_2)\\ \le & C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x)\sum _{j=1}^{\mathrm{\infty }}\mathrm{\omega }\left(6^{-j}\right)\\ \le & C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}$$

And

$$\begin{array}{rl}II{I}_2\le & C\sum _{k=1}^{\mathrm{\infty }}(\frac{1}{{[\lambda (x_Q,6^k{r}_Q)]}^2}{\int }_{6^{k+1}Q}|f_2(y_2)|d\mu (y_2))\\ \times \sum _{j=1}^{k-1}{\int }_{6^{k+1}Q\setminus 6^{k}Q}|f_1(y_1)|d\mu (y_1)\mathrm{\omega }\left(6^{-k}\right)\\ \le & \sum _{k=1}^{\mathrm{\infty }}(\frac{1}{{[\lambda (x_Q,6^k{r}_Q)]}^2}{\int }_{6^{k+1}Q}|f_2(y_2)|d\mu (y_2)){\int }_{6^{k}Q}|f_1(y_1)|d\mu (y_1)\mathrm{\omega }\left(6^{-k}\right)\\ \le & \sum _{k=1}^{\mathrm{\infty }}(C_{\lambda }^{{log}_2^{30}+1}\frac{1}{\lambda (x_Q,5\times 6^{k+1}{r}_Q)}{\int }_{6^{k+1}Q}|f_2(y_2)|d\mu (y_2))\\ \times (C_{\lambda }^{{log}_2^5+1}\frac{1}{\lambda (x_Q,5\times 6^k{r}_Q)}{\int }_{6^{k}Q}|f_1(y_1)|d\mu (y_2))\mathrm{\omega }\left(6^{-k}\right)\\ \le & C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x)\sum _{k=1}^{\mathrm{\infty }}\mathrm{\omega }\left(6^{-k}\right)\\ \le & C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}$$

Therefore,

$$|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y)-T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(z)|{\chi }_Q(y)\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

(2.10)

By the above estimate, we have

$$\begin{array}{rl}II{I}^{\frac{1}{\delta }}& ={\left(\frac{1}{\mu (30Q)}\frac{1}{\mu (Q)}{\int }_Q{\int }_Q\right|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y)-T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(z){|}^{\delta }d\mu (z)d\mu (y))}^{\frac{1}{\delta }}\\ \le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}$$

Fix any balls $Q\subset R$ with $x\in Q$, where Q is an arbitrary ball and R is a doubling ball. Noting that R is a doubling ball we have $R=\tilde{R}$. We denote $N_{Q,R}+1$ by N such that $6R\subset {10}^{N}Q$. Let $f_i^0=f_i{\chi }_{6Q}$, $f_i^N=f_i{\chi }_{{10}^{N}Q}$, $f_i^{Q_N}=f_i{\chi }_{{10}^{N}Q\setminus 6Q}$, $f_i^{\mathrm{\infty }}=f_i{\chi }_{\mathcal{X}\setminus {10}^{N}Q}$, $f_i^R=f_i{\chi }_{6R}$ and $f_i^{R_N}=f_i{\chi }_{{10}^{N}Q\setminus 6R}$, write the difference $h_Q-h_R$ in the following way:

$$\begin{array}{r}|h_Q-h_R|\\ \le \left|m_Q(T_{\mathrm{\omega }}(f_1^0,f_2^{Q_N})+T_{\mathrm{\omega }}(f_1^{Q_N},f_2^0))\right|+\left|m_Q\left(T_{\mathrm{\omega }}(f_1^{Q_N},f_2^{Q_N})\right)\right|\\ +|m_Q\left(T_{\mathrm{\omega }}(f_1^N,f_2^N)\right)-m_R\left(T_{\mathrm{\omega }}(f_1^N,f_2^N)\right)|\\ +|m_Q\left(T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^N)\right)-m_R\left(T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^N)\right)|\\ +|m_Q\left(T_{\mathrm{\omega }}(f_1^N,f_2^{\mathrm{\infty }})\right)-m_R\left(T_{\mathrm{\omega }}(f_1^N,f_2^{\mathrm{\infty }})\right)|\\ +\left|m_R(T_{\mathrm{\omega }}(f_1^R,f_2^{R_N})+T_{\mathrm{\omega }}(f_1^{R_N},f_2^N))\right|+\left|m_R\left(T_{\mathrm{\omega }}(f_1^{R_N},f_2^{R_N})\right)\right|\\ =A_1+A_2+A_3+A_4+A_5+A_6+A_7.\end{array}$$

For the term $A_1$, we, firstly, deal with $T_{\mathrm{\omega }}(f_1^0,f_2^{Q_N})$; it follows from the size of kernel (1.5), for all $y\in Q$,

$$\begin{array}{r}|T_{\mathrm{\omega }}(f_1^0,f_2^{Q_N})(y)|\\ \le C{\int }_{6Q}{\int }_{{10}^{N}Q\setminus 6Q}\frac{|f_1(y_1)||f_2(y_2)|}{{[\lambda (y,d(y,\tilde{y}))]}^2}d\mu (y_2)d\mu (y_1)\\ \le C{\int }_{6Q}\frac{f_1(y_1)}{\lambda (y,d(y,y_2))}d\mu (y_1){\int }_{{10}^{N}Q\setminus 6Q}\frac{f_2(y_2)}{\lambda (y,d(y,y_2))}d\mu (y_2)\\ \le C(\sum _{k=1}^{N_{Q,R}}{\int }_{{10}^{k+1}Q\setminus {10}^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2)+{\int }_{10Q\setminus 6Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2))\\ \times \frac{\mu (5\times 6Q)}{\lambda (x_Q,6r_Q)}\frac{1}{\mu (5\times 6Q)}{\int }_{6Q}|f_1(y_1)|d\mu (y_1)\\ \le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}$$

Using the analogous methods to deal with the term $T_{\mathrm{\omega }}(f_1^{Q_N},f_2^0)$, we have

$$A_1\le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

By an argument similar to the estimate for $A_1$, we see that

$$A_6\le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

For all $y\in Q$, we have

$$\begin{array}{r}|T_{\mathrm{\omega }}(f_1^{Q_N},f_2^{Q_N}(y)|\\ \le C{\int }_{{10}^{N}Q\setminus 6Q}{\int }_{{10}^{N}Q\setminus 6Q}\frac{|f_1(y_1)||f_2(y_2)|}{{[\lambda (y,d(y,\tilde{y}))]}^2}d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{N-1}\sum _{j=1}^{N-1}{\int }_{{10}^{k+1}Q\setminus {10}^{k}Q}{\int }_{{10}^{j+1}Q\setminus {10}^{j}Q}\frac{|f_1(y_1)||f_2(y_2)|}{{[\lambda (y,d(y,\tilde{y}))]}^2}d\mu (y_1)d\mu (y_2)\\ +C{\int }_{10Q\setminus 6Q}{\int }_{10Q\setminus 6Q}\frac{|f_1(y_1)||f_2(y_2)|}{{[\lambda (y,d(y,\tilde{y}))]}^2}d\mu (y_1)d\mu (y_2)\\ =:D_1+D_2.\end{array}$$

Firstly, for $D_2$, we note that $y\in Q$, $y_i\in 10Q\setminus 6Q$, so $5r_Q\le d(y,y_i)\le 11r_Q$, $i=1,2$. The properties of λ imply that

$$\begin{array}{c}\frac{1}{\lambda (y,11r_Q)}\le \frac{1}{\lambda (y,d(y,y_i))}\le \frac{1}{\lambda (y,5r_Q)},\hfill \\ \begin{array}{rl}{D}_2& \le \frac{C}{{[\lambda (y,5r_Q)]}^2}{\int }_{10Q\setminus 6Q}{\int }_{10Q\setminus 6Q}|f_1(y_1)||f_2(y_2)|d\mu (y_1)d\mu (y_2)\\ \le \frac{C}{{[\lambda (x_Q,5r_Q)]}^2}{\int }_{10Q\setminus 6Q}{\int }_{10Q\setminus 6Q}|f_1(y_1)||f_2(y_2)|d\mu (y_1)d\mu (y_2)\\ \le \prod _{i=1}^2\frac{\mu (50Q)}{\lambda (x_Q,5r_Q)}\frac{1}{\mu (50Q)}{\int }_{10Q}|f_i(y_i)|d\mu (y_i)\\ \le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}\hfill \end{array}$$

For $D_1$, we have

$$\begin{array}{rl}{D}_1\le & C\sum _{k=1}^{N-1}\sum _{j=k}^{N-1}{\int }_{{10}^{k+1}Q\setminus {10}^{k}Q}|f_1(y_1)|{\int }_{{10}^{j+1}Q\setminus {10}^{j}Q}\frac{|f_2(y_2)|}{{[\lambda (y,d(y,y_2))]}^2}d\mu (y_2)d\mu (y_1)\\ +\sum _{k=1}^{N-1}\sum _{j=1}^{k-1}{\int }_{{10}^{k+1}Q\setminus {10}^{k}Q}\frac{|f_1(y_1)|}{{[\lambda (y,d(y,y_1))]}^2}{\int }_{{10}^{j+1}Q\setminus {10}^{j}Q}|f_1(y_1)|d\mu (y_2)d\mu (y_1)\\ :=& D_{11}+D_{12}.\end{array}$$

In the following, we will estimate $D_{11}$ and $D_{12}$, respectively:

$$\begin{array}{c}\begin{array}{rl}{D}_{11}& \le \sum _{j=1}^{N-1}\frac{1}{{[\lambda (x_Q,{10}^j{r}_Q)]}^2}{\int }_{{10}^{j+1}Q\setminus {10}^{j}Q}|f_2(y_2)|d\mu (y_2)\sum _{k=1}^j{\int }_{{10}^{k+1}Q\setminus {10}^{k}Q}|f_1(y_1)|d\mu (y_1)\\ \le \sum _{j=1}^{N-1}\frac{1}{{[\lambda (x_Q,{10}^j{r}_Q)]}^2}{\int }_{{10}^{j+1}Q}|f_2(y_2)|d\mu (y_2){\int }_{{10}^{j+1}Q}|f_1(y_1)|d\mu (y_1)\\ \le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x),\end{array}\hfill \\ \begin{array}{rl}{D}_{12}& \le \sum _{k=1}^{N-1}{\int }_{{10}^{k+1}Q\setminus {10}^{k}Q}\frac{|f_1(y_1)|}{{[\lambda (y,d(y,y_1))]}^2}d\mu (y_1){\int }_{{10}^{k}Q}|f_2(y_2)|d\mu (y_2)\\ \le \sum _{k=1}^{N-1}\frac{1}{{[\lambda (x_Q,{10}^k{r}_Q)]}^2}{\int }_{{10}^{k+1}Q}|f_1(y_1)|d\mu (y_1){\int }_{{10}^{k}Q}|f_2(y_2)|d\mu (y_2)\\ \le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).\end{array}\hfill \end{array}$$

The estimates of $D_1$ and $D_2$ imply that

$$A_2\le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

Analogously,

$$A_7\le C{K}_{Q,R}{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

Some estimates similar to $III$ yield

$$A_3\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

Finally, using a similar argument as that of II, which involves the kernel condition (1.6), we obtain

$$A_4+A_5\le C{\mathcal{M}}_{(5)}(\overrightarrow{f})(x).$$

Combining all the estimates for $A_i$ with $i\in \{1,\dots ,7\}$, we get (2.9).

Let us see how from (2.8) and (2.9) one gets (2.7). Use the definition of $M_{\delta }^{\mathrm{♯}}(\overrightarrow{f})(x)$ and the fact $|{|\alpha |}^{\gamma }-{|\beta |}^{\gamma }|\le {|\alpha -\beta |}^{\gamma }$, $0<\gamma <1$, if Q is a doubling ball and $x\in Q$, we have

$$\begin{array}{r}{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|{|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }-m_{\tilde{Q}}\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right)|d\mu (y))}^{\frac{1}{\delta }}\\ \le C{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|{|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }-{|h_Q|}^{\delta }\left|d\mu \right)}^{\frac{1}{\delta }}+C{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|{|h_Q|}^{\delta }-{|h_{\tilde{Q}}|}^{\delta }\left|d\mu \right)}^{\frac{1}{\delta }}\\ +C{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|{|h_{\tilde{Q}}|}^{\delta }-m_{\tilde{Q}}\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right)\left|d\mu \right)}^{\frac{1}{\delta }}\\ \le C{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|T_{\mathrm{\omega }}(\overrightarrow{f})-h_Q{|}^{\delta }d\mu )}^{\frac{1}{\delta }}+C{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|{|h_Q|}^{\delta }-{|h_{\tilde{Q}}|}^{\delta }\left|d\mu \right)}^{\frac{1}{\delta }}\\ +C{\left(\frac{\mu (Q)}{\mu (30Q)}\right)}^{\frac{1}{\delta }}|{|h_{\tilde{Q}}|}^{\delta }-m_{\tilde{Q}}\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right){|}^{\frac{1}{\delta }}\\ \le C{\left(\frac{1}{\mu (30Q)}{\int }_Q\right|T_{\mathrm{\omega }}(\overrightarrow{f})-h_Q{|}^{\delta }d\mu )}^{\frac{1}{\delta }}+C{(\frac{1}{\mu (30Q)}{\int }_Q|h_Q-h_{\tilde{Q}}{|}^{\delta }d\mu )}^{\frac{1}{\delta }}\\ +C{\left(\frac{\mu (Q)}{\mu (30Q)}\right)}^{\frac{1}{\delta }}{\left(\frac{1}{\mu (\tilde{Q})}{\int }_{\tilde{Q}}\right|T_{\mathrm{\omega }}(\overrightarrow{f})-h_{\tilde{Q}}{|}^{\delta }d\mu (y))}^{\frac{1}{\delta }},\end{array}$$

and for all doubling balls $Q\subset R$ with $x\in Q$, we have

$$\begin{array}{r}|m_Q\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right)-m_R\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right){|}^{\frac{1}{\delta }}\\ \le C|m_Q\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right)-{|h_Q|}^{\delta }{|}^{\frac{1}{\delta }}+C|{|h_R|}^{\delta }-m_R\left({|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\right){|}^{\frac{1}{\delta }}+C|{|h_Q|}^{\delta }-{|h_R|}^{\delta }{|}^{\frac{1}{\delta }}\\ \le C{\left(\frac{1}{\mu (Q)}{\int }_Q\right|{|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }-{|h_Q|}^{\delta }\left|d\mu \right)}^{\frac{1}{\delta }}+{\left(\frac{1}{\mu (R)}{\int }_R\right|{|h_R|}^{\delta }-{|T_{\mathrm{\omega }}(\overrightarrow{f})|}^{\delta }\left|d\mu \right)}^{\frac{1}{\delta }}\\ +C|h_Q-h_R|\\ \le C{\left(\frac{1}{\mu (Q)}{\int }_Q\right|T_{\mathrm{\omega }}(\overrightarrow{f})-h_Q{|}^{\delta }d\mu )}^{\frac{1}{\delta }}+{\left(\frac{1}{\mu (R)}{\int }_R\right|h_R-T_{\mathrm{\omega }}(\overrightarrow{f}){|}^{\delta }d\mu )}^{\frac{1}{\delta }}+C|h_Q-h_R|.\end{array}$$

Since we proved (2.8) and (2.9), (2.7) holds obviously. □

Now we give the proof of Theorem 1.5.

Proof Since $L_c^{\mathrm{\infty }}(\mu )$ is dense in $L^p(\mu )$, $1<p<\mathrm{\infty }$, Lemma 2.4 holds for $f_i\in L^{p_i}(\mu )$. Using Lemma 2.3, Hölder’s inequality, and the boundedness of $M_{(k)}(f)$, we get

$$\begin{array}{rl}{\parallel T_{\mathrm{\omega }}(\overrightarrow{f})\parallel }_{L^p(\mu )}& \le {\parallel N_{\delta }(T_{\mathrm{\omega }}(\overrightarrow{f}))\parallel }_{L^p(\mu )}\le C{\parallel M_{\delta }^{\mathrm{♯}}(T_{\mathrm{\omega }}(\overrightarrow{f}))\parallel }_{L^p(\mu )}\le C{\parallel {\mathcal{M}}_{(5)}(\overrightarrow{f})\parallel }_{L^p(\mu )}\\ \le C{\parallel M_{(5)}(f_1)\parallel }_{L^{p_1}(\mu )}{\parallel M_{(5)}(f_2)\parallel }_{L^{p_2}(\mu )}\\ \le C\prod _{i=1}^2{\parallel f_i\parallel }_{L^{p_i}(\mu )}.\end{array}$$

 □

3 Boundedness on Morrey spaces

We recall the definition of the Morrey space with non-doubling measure.

Definition 3.1 Let $k>1$ and $1\le q\le p<\mathrm{\infty }$; the Morrey space $M_q^p(k,\mu )$ is defined as

$$M_q^p(k,\mu ):=\{f\in L_{\mathrm{loc}}^q(\mu );{\parallel f\parallel }_{M_q^p(k,\mu )}<\mathrm{\infty }\}$$

with the norm

$${\parallel f\parallel }_{M_q^p(k,\mu )}:=\underset{Q\in \mathcal{X}}{sup}\mu {(kQ)}^{\frac{1}{p}-\frac{1}{q}}{\left({\int }_Q{|f|}^{q}d\mu \right)}^{\frac{1}{q}}.$$

As is easily seen, the space $M_q^p(k,\mu )$ is a Banach space with its norm. The Morrey space norm reflects local regularity of f more precisely than the Lebesgue space norm. It is easy to see from Hölder’s inequality that $L^p(\mu )=M_p^p(k,\mu )\subset M_{q_1}^p(k,\mu )\subset M_{q_2}^p(k,\mu )$ whenever $1\le q_2\le q_1\le p<\mathrm{\infty }$. Moreover, the definition of the spaces is independent of the constant $k>1$, and the norms for different choice of $k>1$ are equivalent, see [15–18] for details. We will denote $M_q^p(6,\mu )$ by $M_q^p(\mu )$.

For the proof of Theorem 1.6, we need some lemmas.

Lemma 3.2 [19]

Let $Q=Q(x,r)$, $\lambda (x,r)$ satisfying conditions of definition (1.3), $q>1$, $\frac{1}{q}+\frac{1}{q\prime }=1$, then

$${[{\int }_{\mathcal{X}\setminus Q}\frac{1}{{[\lambda (x,d(x,y))]}^{q\prime }}d\mu (y)]}^{\frac{1}{q\prime }}\le C{(\lambda (x,r))}^{-\frac{1}{q}}.$$

Lemma 3.3 Let $1<q<p<\mathrm{\infty }$ and $f\in M_q^p(\mu )$, for $x\in Q(x,r)$, we have

$${\int }_{\mathcal{X}\setminus Q}\frac{|f(y)|}{\lambda (x,d(x,y))}d\mu (y)\le C\mu {(Q)}^{-\frac{1}{q}}{\parallel f\parallel }_{L^q(\mu )}.$$

Proof Using Hölder’s inequality and Lemma 3.2, we get

$$\begin{array}{rl}{\int }_{\mathcal{X}\setminus Q}\frac{|f(y)|}{\lambda (x,d(x,y))}d\mu (y)& \le C{({\int }_{\mathcal{X}\setminus Q}{|f(y)|}^{q}d\mu (y))}^{\frac{1}{q}}{({\int }_{\mathcal{X}\setminus Q}\frac{1}{{[\lambda (x,d(x,y))]}^{q^{\prime }}}d\mu (y))}^{\frac{1}{q^{\prime }}}\\ \le C{\parallel f\parallel }_{L^q(\mu )}{(\lambda (x,r))}^{-\frac{1}{q}},\end{array}$$

since $\mu (Q(x,r))\le \lambda (x,r)$,

$${\int }_{\mathcal{X}\setminus Q}\frac{|f(y)|}{\lambda (x,d(x,y))}d\mu (y)\le C\mu {(Q)}^{-\frac{1}{q}}{\parallel f\parallel }_{L^q(\mu )}.$$

 □

Now we are ready to give the proof of Theorem 1.6.

Proof Fix a ball $Q\in \mathcal{X}$ and we split each $f_i$ as $f_i=f_i^0+f_i^{\mathrm{\infty }}$, where $f_i^0=f_i{\chi }_{2Q}$ and $f_i^{\mathrm{\infty }}=f_i-f_i^0$, and this yields

$$\begin{array}{rl}|T_{\mathrm{\omega }}(\overrightarrow{f})(y)|& =|T_{\mathrm{\omega }}(f_1,f_2)(y)|\\ \le |T_{\mathrm{\omega }}(f_1^0,f_2^0)(y)|+|T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(y)|+|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(y)|+|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y)|\\ :=H_1+H_2+H_3+H_4.\end{array}$$

For the first term $H_1$, using the results of Theorem 1.5, we have

$$\begin{array}{rl}{\parallel T_{\mathrm{\omega }}(f_1^0,f_2^0)\parallel }_{M_q^p(\mu )}& \le \underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}{\left({\int }_Q\right|T_{\mathrm{\omega }}(f_1^0,f_2^0)(y){|}^{q}d\mu (y))}^{\frac{1}{q}}\\ \le \underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}{\parallel T_{\mathrm{\omega }}(f_1^0,f_2^0)\parallel }_{L^q(\mu )}\\ \le C\underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}\prod _{i=1}^2{\parallel f_i^0\parallel }_{L^{q_i}(\mu )}\\ \le C\underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}\prod _{i=1}^2{({\int }_{2Q}|f_i{|}^{q_i}d\mu (y))}^{\frac{1}{q_i}}\\ \le C\underset{Q\in \mathcal{X}}{sup}\prod _{i=1}^2\mu {(6Q)}^{\frac{1}{p_i}-\frac{1}{q_i}}{({\int }_{2Q}|f_i{|}^{q_i}d\mu (y))}^{\frac{1}{q_i}}\\ \le C\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}.\end{array}$$

Considering the case $H_4$, firstly, we deal with $|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})|$. For $y\in Q$, we have

$$\begin{array}{r}\left|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})\right|{\chi }_Q(y)\\ \le C{\int }_{\mathcal{X}\setminus 2Q}{\int }_{\mathcal{X}\setminus 2Q}\frac{|f_1(y_1)||f_2(y_2)|}{{[\lambda (y,d(y,\tilde{y}))]}^2}d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=k}^{\mathrm{\infty }}{\int }_{2^{k+1}Q\setminus 2^{k}Q}|f_2(y_2)|{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{{[\lambda (y,d(y,y_1))]}^2}d\mu (y_1)d\mu (y_2)\\ +C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=1}^{k-1}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{{[\lambda (y,d(y,y_2))]}^2}{\int }_{2^{j+1}Q\setminus 2^{j}Q}|f_1(y_1)|d\mu (y_1)d\mu (y_2)\\ :=E_1+E_2.\end{array}$$

For the term $E_1$, it follows that

$$\begin{array}{rl}{E}_1& =C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=k}^{\mathrm{\infty }}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_1))}{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_1))}d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=k}^{\mathrm{\infty }}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_1))}d\mu (y_1)d\mu (y_2)\\ \le C\sum _{j=1}^{\mathrm{\infty }}{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_1))}d\mu (y_1)\sum _{k=1}^j{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2)\\ \le C\sum _{j=1}^{\mathrm{\infty }}{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_1))}d\mu (y_1){\int }_{2^{j+1}Q\setminus 2Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2)\\ \le C\prod _{i=1}^2{\int }_{\mathcal{X}\setminus 2Q}\frac{|f_i(y_i)|}{\lambda (y,d(y,y_i))}d\mu (y_i).\end{array}$$

And

$$\begin{array}{rl}{E}_2& =C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=1}^{k-1}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_2))}d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{\mathrm{\infty }}\sum _{j=1}^{k-1}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}{\int }_{2^{j+1}Q\setminus 2^{j}Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_1))}d\mu (y_1)d\mu (y_2)\\ \le C\sum _{k=1}^{\mathrm{\infty }}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2){\int }_{2^{k}Q\setminus 2Q}\frac{|f_1(y_1)|}{\lambda (y,d(y,y_1))}d\mu (y_1)\\ \le C\prod _{i=1}^2{\int }_{\mathcal{X}\setminus 2Q}\frac{|f_i(y_i)|}{\lambda (y,d(y,y_i))}d\mu (y_i).\end{array}$$

For the term ${\prod }_{i=1}^2{\int }_{\mathcal{X}\setminus 2Q}\frac{|f_i(y_i)|}{\lambda (y,d(y,y_i))}d\mu (y_i)$, using Lemma 3.3, we get

$$\begin{array}{rl}\prod _{i=1}^2{\int }_{\mathcal{X}\setminus 2Q}\frac{|f_i(y_i)|}{\lambda (y,d(y,y_i))}d\mu (y_i)& \le C\prod _{i=1}^2\mu {(2Q)}^{-\frac{1}{q_i}}{\parallel f_i\parallel }_{L^{q_i}(\mu )}\\ =C\prod _{i=1}^2\mu {(2Q)}^{-\frac{1}{q_i}}\mu {(6Q)}^{-\frac{1}{p_i}+\frac{1}{q_i}}\mu {(6Q)}^{\frac{1}{p_i}-\frac{1}{q_i}}{\parallel f_i\parallel }_{L^{q_i}(\mu )}\\ \le C{\left(\frac{\mu (6Q)}{\mu (2Q)}\right)}^{\frac{1}{q}}\mu {(6Q)}^{-\frac{1}{p}}\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}.\end{array}$$

According to the estimate above, we obtain

$$\begin{array}{r}{\parallel T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})\parallel }_{M_q^p(\mu )}\\ \le \underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}{\left({\int }_Q\right|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^{\mathrm{\infty }})(y){|}^{q}d\mu (y))}^{\frac{1}{q}}\\ \le C\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}\mu {(Q)}^{\frac{1}{q}}{\left(\frac{\mu (6Q)}{\mu (2Q)}\right)}^{\frac{1}{q}}\mu {(6Q)}^{-\frac{1}{p}}\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}\\ \le C\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}.\end{array}$$

What remain to be considered are the terms in $H_2$ and $H_3$. For $H_2$, we use the size condition of kernel (1.5) and the property of $\lambda :\lambda (y,r)\approx \lambda (x,r)$, $d(x,y)\le r$,

$$\begin{array}{rl}|T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(y)|& \le C{\int }_{2Q}|f_1(y_1)|{\int }_{\mathcal{X}\setminus 2Q}\frac{|f_2(y_2)|}{{[\lambda (y,d(y,y_2))]}^2}d\mu (y_2)d\mu (y_1)\\ \le C{\int }_{2Q}|f_1(y_1)|\sum _{k=1}^{\mathrm{\infty }}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{{[\lambda (y,d(y,y_2))]}^2}d\mu (y_2)d\mu (y_1)\\ \le C{\int }_{2Q}|f_1(y_1)|\frac{1}{\lambda (x_Q,2^k{r}_Q)}\sum _{k=1}^{\mathrm{\infty }}{\int }_{2^{k+1}Q\setminus 2^{k}Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2)d\mu (y_1)\\ \le C\mu {(2Q)}^{-1}{\int }_{2Q}|f_1(y_1)|d\mu (y_1){\int }_{\mathcal{X}\setminus 2Q}\frac{|f_2(y_2)|}{\lambda (y,d(y,y_2))}d\mu (y_2)\\ \le C\mu {(2Q)}^{-1}{(\mu (2Q))}^{1-\frac{1}{q_1}}{\parallel f_1\parallel }_{L^{q_1}(\mu )}{(\mu (2Q))}^{-\frac{1}{q_2}}{\parallel f_2\parallel }_{L^{q_2}(\mu )}\\ \le C{\left(\frac{\mu (6Q)}{\mu (2Q)}\right)}^{\frac{1}{q}}\mu {(6Q)}^{-\frac{1}{p}}\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}.\end{array}$$

Then using the above estimate, we get

$$\begin{array}{rl}{\parallel T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})\parallel }_{M_q^p(\mu )}& \le \underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}{\left({\int }_Q\right|T_{\mathrm{\omega }}(f_1^0,f_2^{\mathrm{\infty }})(y){|}^{q}d\mu (y))}^{\frac{1}{q}}\\ \le C\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}.\end{array}$$

Analogously, for $H_3$, we have

$$\begin{array}{rl}{\parallel T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)\parallel }_{M_q^p(\mu )}& \le \underset{Q\in \mathcal{X}}{sup}\mu {(6Q)}^{\frac{1}{p}-\frac{1}{q}}{\left({\int }_Q\right|T_{\mathrm{\omega }}(f_1^{\mathrm{\infty }},f_2^0)(y){|}^{q}d\mu (y))}^{\frac{1}{q}}\\ \le C\prod _{i=1}^2{\parallel f_i\parallel }_{M_{q_i}^{p_i}(\mu )}.\end{array}$$

 □