- Research
- Open access
- Published:
Bernstein-Jackson-type inequalities and Besov spaces associated with unbounded operators
Journal of Inequalities and Applications volume 2014, Article number: 105 (2014)
Abstract
Besov-type interpolation spaces and appropriate Bernstein-Jackson inequalities, generated by unbounded linear operators in a Banach space, are considered. In the case of the operator of differentiation these spaces and inequalities exactly coincide with the classical ones. Inequalities are applied to a best approximation problem in a Banach space, particularly, to spectral approximations of regular elliptic operators.
MSC:47A58, 41A17.
1 Introduction and preliminaries
The classical Jackson and Bernstein inequalities express a relation between smoothness modules of functions and properties of their best approximations by polynomials or entire functions of exponential type that can be characterized with the help of Besov norms [[1], Sections 1.5, 7.2]. These results are extended to approximations of smooth functions by wavelets (see e.g. [2–4]), and to approximations of linear operators in Banach spaces by operators with finite ranks [5], and other similar approximations.
The motivation of our work is to extend the Bernstein-Jackson inequalities to cases of best spectral approximations in a Banach space. An analog of Bernstein-Jackson inequalities in the case of approximations in the space on a Lie group G by spectral subspaces of the group sublaplacian , where is its spectral resolution, is established in [6, 7]. Spectral subspaces are analogous subspaces of entire functions of exponential type. The appropriate Besov space is characterized by the functional of best approximation .
This approach is a prototype of our generalizations. We consider a closed operator A in a Banach space 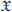 instead of and replace the spectral subspaces by invariant subspaces of exponential type entire vectors of A. Note that similar subspaces of exponential type entire vectors have appeared in [8–11].
instead of and replace the spectral subspaces by invariant subspaces of exponential type entire vectors of A. Note that similar subspaces of exponential type entire vectors have appeared in [8–11].
Our goal is to investigate a best approximation problem by invariant subspaces of exponential type entire vectors of an arbitrary unbounded closed linear operator A in a Banach space 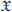 . As a basic tool, we use an analog of approximate Bernstein and Jackson inequalities and an abstract quasi-normed Besov-type interpolation space , associated with exponential type entire vectors of A, which sharply characterizes the behavior of the best spectral approximation.
. As a basic tool, we use an analog of approximate Bernstein and Jackson inequalities and an abstract quasi-normed Besov-type interpolation space , associated with exponential type entire vectors of A, which sharply characterizes the behavior of the best spectral approximation.
Using the quasi-norm of , the main result is formulated in Theorem 5 as two inequalities, estimating the minimal distance from a given element to a subspace of exponential type vectors with fixed indices. In the case of the operator of differentiation in , the spaces coincide with the classical Besov-type spaces (Theorem 7) and the estimations reduce to the known Bernstein and Jackson inequalities (Theorem 8). A new application to spectral approximations of elliptic operators is shown in Section 6 (see also Theorem 6).
In a Banach complex space we consider a closed unbounded linear operator with the norm dense domain ,
Let and . We call the elements
exponential type entire vectors of A, where the constant is independent on and is the unit operator on 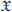 . Clearly, every exponential type entire vector also is an analytic vector of A in the well-known Nelson sense.
. Clearly, every exponential type entire vector also is an analytic vector of A in the well-known Nelson sense.
Throughout this article we assume that the norm density condition holds and that the operators () are closed in 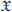 . In many important cases for applications these assumptions hold. Particularly, we have the cases:
. In many important cases for applications these assumptions hold. Particularly, we have the cases:
-
(i)
if A has a real spectrum and the integral with is convergent (see [8]);
-
(ii)
if A generates we have an one-parameter group with the convergent integral [8];
-
(iii)
if A generates we have a bounded -group on
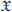 (see [10]).
(see [10]).
If () and is the differentiation operator on ℝ then is the space of entire functions of exponential type, belonging to . In this case the inequality reduces to the Bernstein inequality. If the spectrum of an operator A is discrete then the subspace exactly coincides with the linear span of all its spectral subspaces in 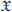 (see [12]).
(see [12]).
Recall the real interpolation method (for more details see [1, 13]). Let and be a quasi-normed complex spaces. Given the pair positive numbers or the interpolation vector space can be defined as the set endowed with the quasi-norm
where is called a K-functional [[1], Section 3.11]. Clearly, .
2 Scales of invariant subspaces
Let and . Consider the mapping
which image is formed by sequences of elements of a Banach space 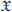 . For any pair of indices t, p we define the normed spaces , where
. For any pair of indices t, p we define the normed spaces , where
Theorem 1
-
(i)
The contractive inclusions with hold.
-
(ii)
Every space is A-invariant and the restriction is a bounded operator over with the norm .
-
(iii)
The spectrum of A has the property .
-
(iv)
Every space is complete.
Proof
-
(i)
The inequalities and yield the contractive inclusions and , respectively. If then and for all . It follows that . Therefore, for any the series is convergent. As a result, . Moreover, for all and .
-
(ii)
Using , we obtain and when .
-
(iii)
For any and the equality holds. It follows that for all . Hence, λ belongs to the resolvent set .
-
(iv)
Let us use the inequality with , . It follows that if is a Cauchy sequence in the space then and are Cauchy sequences in the space
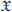 for all . The completeness of
for all . The completeness of 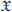 implies that there exist such that and by norm of
implies that there exist such that and by norm of 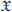 . The graph of is closed in , therefore and . It is true for all , so and by norm of
. The graph of is closed in , therefore and . It is true for all , so and by norm of 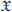 for all .
for all .
We reason standardly: , . It follows that , , . So, and for . Hence, from it follows that for all . We may use the fact that the scalar sequences with and belong to the Banach space . Calculating -norms of these elements and applying the previous inequality, we obtain
Hence, . Moreover, , where in this inequality all sequences by k belong to . We obtain , . So, is complete. □
On the subspace we define the function
Theorem 2
-
(i)
For every p () the embedding with and the equality hold.
-
(ii)
The function (2) is a quasi-norm satisfying the inequality for all . Moreover, the contractive embedding is true.
Proof (i) Let . We reason similarly to the above. For every we have . So . It follows that . Therefore, for every the series is convergent, i.e. . Hence, .
The constant c in the definition is independent on the index . It yields the equality . Hence, . Therefore, the embedding from Theorem 2(i) yields the embedding for any index p. The inverse embedding follows from Theorem 1(i).
(ii) Use that and set . For each and the values , are finite and the inequalities
with hold. It follows that . Since ε is arbitrary, for all . Evidently, for all . So is a quasi-norm. The contractility of is a direct consequence of (2). □
3 Besov-type scales of approximation spaces
Let . In what follows we denote by the subspace endowed with the quasi-norm . Consider the auxiliary functional
Given a pair of numbers and we consider the scale of spaces ,
where by [[1], Lemma 7.1.6] the function is a quasi-norm on .
We can call the space endowed with the quasi-norm an abstract Besov-type space, determined by an operator A. The following properties of are deduced from well-known interpolation theorems.
Theorem 3 (i) If is the space endowed with the quasi-norm with then the equality
(up to a quasi-norm equivalence) holds.
-
(ii)
The spaces are complete.
-
(iii)
If , , with then
(4)
and there exist constants , such that
-
(iv)
If then the following continuous embedding holds:
(7)
Proof (i) The equality (3) is a direct consequence of the definition and [[1], Theorem 7.1.7].
-
(ii)
To prove the completeness of , we equip the sum (which is equal to
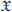 , because ) with the norm with and . Since , we have . Hence, the space
, because ) with the norm with and . Since , we have . Hence, the space 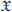 with the norm is complete. Consequently, every series with such that is convergent to an element . Using the inequality , we obtain . So is complete. The isomorphism (3) implies that the space is complete. Thus, is complete as well.
with the norm is complete. Consequently, every series with such that is convergent to an element . Using the inequality , we obtain . So is complete. The isomorphism (3) implies that the space is complete. Thus, is complete as well. -
(iii)
Applying the reiteration property of the real interpolation [[1], Theorem 3.11.5] for the indices with (), , and , we obtain
(8)
Applying the interpolation degree property [[1], Theorem 3.11.6], we obtain
The equalities (8) and (9) for yield (4) with . The inequalities (5), (6) are a consequence of (4) and the well-known interpolation properties [[1], Theorem 3.11.2].
-
(iv)
For every there exists such that
Hence, the embedding is continuous. Finally using (4), we obtain (7). □
Corollary 4 If is norm dense in 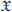 then is as well.
then is as well.
4 Bernstein-Jackson-type inequalities
Let and let the space be endowed with the quasi-norm . Consider the problem of the approximation of a given element in a Banach space 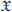 by elements of an A-invariant subspace with a fixed index p. The distance between and we denote by
by elements of an A-invariant subspace with a fixed index p. The distance between and we denote by
To investigate this problem, we will use spaces defined for pair indices or .
Theorem 5 There are constants and such that the following inequalities hold:
Proof Via Theorem 3(i) the space is interpolating between and 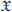 for any and . As a consequence, . Hence, by [[1], Theorem 3.11.4(b)] for some constant we obtain
for any and . As a consequence, . Hence, by [[1], Theorem 3.11.4(b)] for some constant we obtain
This inequality and the isomorphism (3) imply that there is a constant such that the inequality (10) is true. By [[1], Theorem 3.11.4(a)] for some constant we have
Hence, by virtue of the isomorphism (3) there is a constant such that
Following [[1], Section 7.1], we introduce the function
From the inequality it follows that
By [[1], Lemma 7.1.2] for every there exists such that
So, for every there is such that . For any fixed x the function is decreasing, so . Hence, we have . As a result,
Using (12), we have . Putting , we obtain
If , then , where . Therefore, for all numbers such that . By Theorem 1(i), we have . Therefore, . Hence, the inequality
holds. Taking in (13) and using (14), we obtain (11). □
Theorem 6 Let A be an operator with the discrete spectrum , and let be the complex linear span of all , where is the root subspace of A corresponding to . Then for every α, τ there is a constant c such that
Proof In [12] it is proven that for operators A, having discrete spectra, the equality holds. Hence, the inequality (11) directly implies the estimation (15) for the distance from an element to the spectral subspace . □
5 Connections with classical results
Let us put , where is the closure in () of the operator of differentiation. In the considered case we have , where (). Thus, .
Consider the space of entire complex functions of exponential type , belonging to for . Denote . Following [[1], Section 7.2], we can define on the quasi-norm
where is a support of the Fourier-image Fu of a function .
For any pair or and we define the classical Besov space with the norm (see e.g. [[1], Section 6.2]). Let us show a relationship between the spaces and .
Theorem 7 The following isomorphism holds:
Proof Let us denote for any , where , . For every such entire function u the Bernstein inequality for all holds (see [[1], Section 7.2]). It follows that
Hence, if then .
Vice versa, let with a fixed . The norm definition in implies that for all . It follows that
for any function such that for all . Hence, for all . The above inequality implies that if than .
Show that for . From Sobolev’s embedding theorem (see [[14], Chapter I, Section 8, Theorem 1] or [[13], Theorem 2.8.1]) we have
Consequently, for all . Now using the inequality , we have
for all . Hence, for all . So, up to the restriction , we have
Now applying (3), (16) and the well-known interpolation properties of Besov spaces (see [[1], Theorem 7.2.4]), we obtain the required equality:
with and . □
Theorem 8 There exist constants and such that
where .
Proof Using the first equality (16) and the Paley-Wiener theorem, we obtain
Hence, the quasi-norms and are equal on . Now the above claims is a consequence of Theorems 5, 7. □
Note that the equalities (17) and (18) exactly coincide with the well-known Bernstein and Jackson inequalities in the form given in [[1], Section 7.2].
6 An application to regular elliptic operators
Let be an open bounded domain with the infinitely smooth boundary ∂ Ω and the system of operators
is regular elliptic (see e.g. [[13], Section 5.2.1]). Denote , where and for all , .
In the complex space () we consider the closed linear operator
where and is the classical Sobolev space. As is well known [[13], Section 5.4.4], A has a discrete spectrum and the corresponding root subspaces are independent of q. The subspaces of the root vectors belong to the closed subspaces in ,
endowed with the seminorms , .
Theorem 9 The following topological isomorphism holds:
where and is the Besov space.
Proof Consider the space endowed with the norm
Check that the union coincides with the space of all entire analytic functions of exponential type, which restrictions to Ω belong to . The space we endow with the quasi-norm
For simplicity we put . If and then the Sobolev embedding theorem yields
where the constants c, are independent of k. It follows that (see [10])
for all and , where the constant is independent of . Hence, u has an entire analytic extension onto of exponential type.
Conversely, let an entire function u satisfy (22). Then the inequality for all and holds. Here the constant is independent of k. By boundedness of Ω we have
It follows that and consequently , because
Using the inequality (21), (23), and the Paley-Wiener theorem, we obtain the quasi-norm equivalence
where denotes the support of the Fourier-image Fv of a function .
Applying [[13], Theorem 4.2.2], [[1], Theorem 7.1.7] and the Bernstein-Jackson inequalities from [[1], Section 7.2], we find that for any there exists a constant such that
Following Section 3, we define the space
where . Using the inequality (24) and well-known theorems [[1], Theorems 3.11.5, 3.11.6, 7.1.7], [[13], Theorem 2.4.2/2], we obtain
Now let us prove the equality
By [[13], Theorem 5.4.3] for any there exist positive numbers c and C such that
It follows that we have the inequalities
with a constant . Thus, the embedding with holds. Conversely, let . Then
It follows that . Using (25) and (26), we obtain the required equality (20). □
Corollary 10 There exist constants and such that
where . In particular, for every α, τ there is a constant c such that
where is the complex linear span of root subspaces of the operator (19).
Proof From the inequality (27)-(28) and the Paley-Wiener theorem it follows that we have the quasi-norm equivalence on . It remains to apply Theorems 5, 6, and 9. □
References
Bergh J, Löfström J: Interpolation Spaces. Springer, Berlin; 1976.
DeVore R, Lorentz G: Constructive Approximation. Springer, Berlin; 1992.
Garrigós G, Tabacco A: Wavelet decompositions of anisotropic Besov spaces. Math. Nachr. 2002, 239/240: 80-102. 10.1002/1522-2616(200206)239:1<80::AID-MANA80>3.0.CO;2-3
Garrigós G, Hernández E: Sharp Jackson and Bernstein inequalities for n -term approximation in sequence spaces with applications. Indiana Univ. Math. J. 2004,53(6):1741-1764. 10.1512/iumj.2004.53.2552
Carl B: Inequalities of Bernstein-Jackson-type and degree of compactness of operators in Banach spaces. Ann. Inst. Fourier 1985,35(3):79-118. 10.5802/aif.1020
Giulini S: Bernstain and Jackson theorems for the Heisenberg group. J. Aust. Math. Soc. 1985, 38: 241-254. 10.1017/S1446788700023107
Giulini S: Approximation and Besov spaces on stratified groups. Proc. Am. Math. Soc. 1986,96(4):1741-1764.
Ljubič JI, Macaev VI: On operators with separable spectrum. Transl. Am. Math. Soc. 1965, 47: 89-129.
Sakai S: Operator Algebras in Dynamic Systems. Cambridge University Press, Cambridge; 1991.
Radyno YV: Vectors of exponential type in operators calculus and differential equations. Differ. Equ. 1985,21(9):1559-1569.
Gorbachuk MI, Gorbachuk VI: On approximation of smooth vectors of a closed operator by entire vectors of exponential type. Ukr. Math. J. 1995,47(5):713-726. 10.1007/BF01059045
Dmytryshyn M, Lopushansky O: Operator calculus on the exponential type vectors of operators with point spectrum. In Topology in Banach Spaces. Edited by: Banakh T. Nova Publ., New York; 2001:137-145.
Triebel H: Interpolation Theory. Function Spaces. Differential Operators. Springer, Berlin; 1995.
Sobolev SL Transl. Math. Monographs 90. In Some Applications of Functional Analysis in Mathematical Physics. Am. Math. Soc., New York; 2008.
Acknowledgements
The second author was partially supported by the Centre for Innovation and Transfer of Natural Sciences and Engineering Knowledge at the University of Rzeszów.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dmytryshyn, M., Lopushansky, O. Bernstein-Jackson-type inequalities and Besov spaces associated with unbounded operators. J Inequal Appl 2014, 105 (2014). https://doi.org/10.1186/1029-242X-2014-105
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2014-105