Mazur-Ulam theorem under weaker conditions in the framework of 2-fuzzy 2-normed linear spaces

Abstract

The purpose of this paper is to prove that every 2-isometry without any other conditions from a fuzzy 2-normed linear space to another fuzzy 2-normed linear space is affine, and to give a new result of the Mazur-Ulam theorem for 2-isometry in the framework of 2-fuzzy 2-normed linear spaces.

MSC:03E72, 46B20, 51M25, 46B04, 46S40.

1 Introduction

A satisfactory theory of 2-norm and n-norm on a linear space has been introduced and developed by Gähler in [1, 2]. Freese and Cho [3] gave some isometry conditions in linear 2-normed spaces. Raja and Vaezpour [4] introduced the notion of 2-normed hyperset in a hypervector and also constructed some special 2-normed hypersets of strong homomorphisms over hypervector spaces. Different authors introduced the definitions of fuzzy norms on a linear space. For reference, one may see [5]. Following Cheng and Mordeson [6], Bag and Samanta [7] introduced the concept of fuzzy norm on a linear space.

Somasundaram and Beaula [8] introduced the concept of 2-fuzzy 2-normed linear space or fuzzy 2-normed linear space of the set of all fuzzy sets of a set. They gave the notion of α-2-norm on a linear space corresponding to a 2-fuzzy 2-norm with the help of [7] and also gave some fundamental properties of this space.

Let X and Y be metric spaces. A mapping $f:X\to Y$ is called an isometry if f satisfies $d_Y(f(x),f(y))=d_X(x,y)$ for all $x,y\in X$, where $d_X(\cdot ,\cdot )$ and $d_Y(\cdot ,\cdot )$ denote the metrics in the spaces X and Y, respectively. Two metric spaces X and Y are defined to be isometric if there exists an isometry of X onto Y. In 1932, Mazur and Ulam [9] proved the following theorem.

Mazur-Ulam theorem Every isometry of a real normed linear space onto a real normed linear space is a linear mapping up to translation.

Baker [10] showed that an isometry from a real normed linear space into a strictly convex real normed linear space is affine. Also, Jian [11] investigated the generalizations of the Mazur-Ulam theorem in $F^{\ast }$-spaces. Th.M. Rassias and Wagner [12] described all volume preserving mappings from a real finite dimensional vector space into itself and Väisälä [13] gave a short and simple proof of the Mazur-Ulam theorem. Chu [14] proved that the Mazur-Ulam theorem holds when X is a linear 2-normed space. Chu et al. [15] generalized the Mazur-Ulam theorem when X is a linear n-normed space, that is, the Mazur-Ulam theorem holds, when the n-isometry mapped to a linear n-normed space is affine. They also obtained extensions of Th.M. Rassias and Šemrl’s theorem [16]. The Mazur-Ulam theorem has been extensively studied by many authors in different aspects (see [12, 17–20]).

Recently, Cho et al. [21] investigated the Mazur-Ulam theorem on probabilistic 2-normed spaces. Moslehian and Sadeghi [22] investigated the Mazur-Ulam theorem in non-Archimedean spaces. Choy and Ku [23] proved that the barycenter of a triangle carries the barycenter of a corresponding triangle. They showed the Mazur-Ulam problem on non-Archimedean 2-normed spaces using the above statement. Chen and Song [24] introduced the concept of weak n-isometry, and then they got that under some conditions a weak n-isometry is also an n-isometry. Alaca [25] gave the concepts of 2-isometry, collinearity, 2-Lipschitz mapping in 2-fuzzy 2-normed linear spaces. Also, he gave a new generalization of the Mazur-Ulam theorem when X is a 2-fuzzy 2-normed linear space or $\mathrm{\Im }(X)$ is a fuzzy 2-normed linear space. Park and Alaca [26] introduced the concept of 2-fuzzy n-normed linear space or fuzzy n-normed linear space of the set of all fuzzy sets of a non-empty set. They defined the concepts of n-isometry, n-collinearity, n-Lipschitz mapping in this space. Also, they generalized the Mazur-Ulam theorem, that is, when X is a 2-fuzzy n-normed linear space or $\mathrm{\Im }(X)$ is a fuzzy n-normed linear space, the Mazur-Ulam theorem holds. Moreover, it is shown that each n-isometry in 2-fuzzy n-normed linear spaces is affine. Ren [27] showed that every generalized area n preserving mapping between real 2-normed linear spaces X and Y which is strictly convex is affine under some conditions.

In the present paper, we give a new version of Mazur-Ulam theorem with a new method when X is a 2-fuzzy 2-normed linear space or $\mathrm{\Im }(X)$ is a fuzzy 2-normed linear space.

2 On 2-fuzzy 2-normed linear spaces

In this section, at first we give the concept of linear 2-normed space and later the concept of 2-fuzzy 2-normed linear space and its fundamental properties with help of [8]. For more details, we refer the readers to [7, 8, 28, 29].

Definition 2.1 [28]

Let X be a real vector space of dimension greater than 1 and let $\parallel •,•\parallel$ be a real-valued function on $X\times X$ satisfying the following four properties:

• (1) $\parallel x,y\parallel =0$ if and only if x and y are linearly dependent,

• (2) $\parallel x,y\parallel =\parallel y,x\parallel$,

• (3) $\parallel x,\alpha y\parallel =|\alpha |\parallel x,y\parallel$ for any $\alpha \in \mathbb{R}$,

• (4) $\parallel x,y+z\parallel \le \parallel x,y\parallel +\parallel x,z\parallel$,

$\parallel •,•\parallel$ is called a 2-norm on X and the pair $(X,\parallel •,•\parallel )$ is called a linear 2-normed space.

Definition 2.2 [7]

Let X be a linear space over S (a field of real or complex numbers). A fuzzy subset N of $X\times \mathbb{R}$ (ℝ, the set of real numbers) is called a fuzzy norm on X if and only if:

(N1) For all $t\in \mathbb{R}$ with $t\le 0$, $N(x,t)=0$,

(N2) For all $t\in \mathbb{R}$ with $t>0$, $N(x,t)=1$ if and only if $x=0$,

(N3) For all $t\in \mathbb{R}$ with $t>0$, $N(\lambda x,t)=N(x,\frac{t}{|\lambda |})$, if $\lambda \ne 0$, $\lambda \in S$,

(N4) For all $s,t\in \mathbb{R}$, $x,y\in X$, $N(x+y,s+t)\ge min\{N(x,s),N(y,t)\}$,

(N5) $N(x,\cdot )$ is a non-decreasing function of $t\in \mathbb{R}$ and ${lim}_{t\to \mathrm{\infty }}N(x,t)=1$.

Then $(X,N)$ is called a fuzzy normed linear space or, in short, f-NLS.

Theorem 2.1 [7]

Let $(X,N)$ be an f-NLS. Assume the condition that

(N6) $N(x,t)>0$ for all $t>0$ implies $x=0$.

Define ${\parallel x\parallel }_{\alpha }=inf\{t:N(x,t)\ge \alpha \}$, $\alpha \in (0,1)$. Then $\{{\parallel •\parallel }_{\alpha }:\alpha \in (0,1)\}$ is an ascending family of norms on X. We call these norms α-norms on X corresponding to the fuzzy norm on X.

Definition 2.3 Let X be any non-empty set and $\mathrm{\Im }(X)$ be the set of all fuzzy sets on X. For $U,V\in \mathrm{\Im }(X)$ and $\lambda \in S$ the field of real numbers, define

$$U+V=\{(x+y,\nu \wedge \mu ):(x,\nu )\in U,(y,\mu )\in V\}$$

and $\lambda U=\{(\lambda x,\nu ):(x,\nu )\in U\}$.

Definition 2.4 A fuzzy linear space $\hat{X}=X\times (0,1]$ over the number field S, where the addition and scalar multiplication operation on X are defined by $(x,\nu )+(y,\mu )=(x+y,\nu \wedge \mu )$, $\lambda (x,\nu )=(\lambda x,\nu )$ is a fuzzy normed space if to every $(x,\nu )\in \hat{X}$, there is associated a non-negative real number, $\parallel (x,\nu )\parallel$, called the fuzzy norm of $(x,\nu )$, in such a way that

• (i) $\parallel (x,\nu )\parallel =0$ iff $x=0$ the zero element of X, $\nu \in (0,1]$,

• (ii) $\parallel \lambda (x,\nu )\parallel =|\lambda |\parallel (x,\nu )\parallel$ for all $(x,\nu )\in \hat{X}$ and all $\lambda \in S$,

• (iii) $\parallel (x,\nu )+(y,\mu )\parallel \le \parallel (x,\nu \wedge \mu )\parallel +\parallel (y,\nu \wedge \mu )\parallel$ for all $(x,\nu ),(y,\mu )\in \hat{X}$,

• (iv) $\parallel (x,{\bigvee }_t{\nu }_t)\parallel ={\bigwedge }_t\parallel (x,{\nu }_t)\parallel$ for all ${\nu }_t\in (0,1]$.

Definition 2.5 [8]

Let X be a non-empty and $\mathrm{\Im }(X)$ be the set of all fuzzy sets in X. If $f\in \mathrm{\Im }(X)$, then $f=\{(x,\mu ):x\in X\text{ and }\mu \in (0,1]\}$. Clearly, f is a bounded function for $|f(x)|\le 1$. Let S be the space of real numbers, then $\mathrm{\Im }(X)$ is a linear space over the field S where the addition and multiplication are defined by

$$f+g=\{(x,\mu )+(y,\eta )\}=\{(x+y,\mu \wedge \eta ):(x,\mu )\in f\text{ and }(y,\eta )\in g\}$$

and

$$\lambda f=\{(\lambda x,\mu ):(x,\mu )\in f\},$$

where $\lambda \in S$.

The linear space $\mathrm{\Im }(X)$ is said to be a normed space if for every $f\in \mathrm{\Im }(X)$, there is associated a non-negative real number $\parallel f\parallel$ called the norm of f in such a way that

• (i) $\parallel f\parallel =0$ if and only if $f=0$. For

  

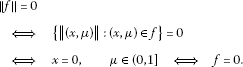
• (ii) $\parallel \lambda f\parallel =|\lambda |\parallel f\parallel$, $\lambda \in S$. For

  $$\begin{array}{rcl}\parallel \lambda f\parallel & =& \{\parallel \lambda (x,\mu )\parallel :(x,\mu )\in f,\lambda \in S\}\\ =& \{|\lambda |\parallel (x,\mu )\parallel :(x,\mu )\in f\}=|\lambda |\parallel f\parallel .\end{array}$$

• (iii) $\parallel f+g\parallel \le \parallel f\parallel +\parallel g\parallel$ for every $f,g\in \mathrm{\Im }(X)$. For

  $$\begin{array}{rcl}\parallel f+g\parallel & =& \{\parallel (x,\mu )+(y,\eta )\parallel :x,y\in X,\mu ,\eta \in (0,1]\}\\ =& \{\parallel (x+y),(\mu \wedge \eta )\parallel :x,y\in X,\mu ,\eta \in (0,1]\}\\ =& \{\parallel (x,\mu \wedge \eta )\parallel +\parallel (y,\mu \wedge \eta )\parallel :(x,\mu )\in f,(y,\eta )\in g\}\\ =& \parallel f\parallel +\parallel g\parallel .\end{array}$$

Then $(\mathrm{\Im }(X),\parallel •\parallel )$ is a normed linear space.

Definition 2.6 [8]

A 2-fuzzy set on X is a fuzzy set on $\mathrm{\Im }(X)$.

Definition 2.7 [8]

Let $\mathrm{\Im }(X)$ be a linear space over the real field S. A fuzzy subset N of $\mathrm{\Im }(X)\times \mathrm{\Im }(X)\times \mathbb{R}$ (ℝ, a set of real numbers) is called a 2-fuzzy 2-norm on X (or a fuzzy 2-norm on $\mathrm{\Im }(X)$) if and only if

(2-N1) for all $t\in \mathbb{R}$ with $t\le 0$, $N(f_1,f_2,t)=0$,

(2-N2) for all $t\in \mathbb{R}$ with $t>0$, $N(f_1,f_2,t)=1$ if and only if $f_1$ and $f_2$ are linearly dependent,

(2-N3) $N(f_1,f_2,t)$ is invariant under any permutation of $f_1$, $f_2$,

(2-N4) for all $t\in \mathbb{R}$ with $t>0$, $N(f_1,\lambda f_2,t)=N(f_1,f_2,\frac{t}{|\lambda |})$, if $\lambda \ne 0$, $\lambda \in S$,

(2-N5) for all $s,t\in \mathbb{R}$,

$$N(f_1,f_2+f_3,s+t)\ge min\{N(f_1,f_2,s),N(f_1,f_3,t)\},$$

(2-N6) $N(f_1,f_2,\cdot ):(0,\mathrm{\infty })\to [0,1]$ is continuous,

(2-N7) ${lim}_{t\to \mathrm{\infty }}N(f_1,f_2,t)=1$.

Then $(\mathrm{\Im }(X),N)$ is a fuzzy 2-normed linear space or $(X,N)$ is a 2-fuzzy 2-normed linear space.

Remark 2.1 In a 2-fuzzy 2-normed linear space $(X,N)$, $N(f_1,f_2,\cdot )$ is a non-decreasing function of ℝ for all $f_1,f_2\in \mathrm{\Im }(X)$.

Theorem 2.2 [8]

Let $(\mathrm{\Im }(X),N)$ be a fuzzy 2-normed linear space. Assume that

(2-N8) $N(f_1,f_2,t)>0$ for all $t>0$ implies $f_1$ and $f_2$ are linearly dependent.

Define ${\parallel f_1,f_2\parallel }_{\alpha }=inf\{t:N(f_1,f_{2}t)\ge \alpha ,\alpha \in (0,1)\}$.

Then $\{{\parallel •,•\parallel }_{\alpha }:\alpha \in (0,1)\}$ is an ascending family of 2-norms on $\mathrm{\Im }(X)$. These 2-norms are called α-2-norms on $\mathrm{\Im }(X)$ corresponding to the 2-fuzzy 2-norm on X.

3 On the Mazur-Ulam theorem

Recently, Alaca [25] introduced the concept of 2-isometry which is suitable to represent the notion of area-preserving mappings in fuzzy 2-normed linear spaces as follows.

For $f,g,h\in \mathrm{\Im }(X)$ and $\alpha ,\beta \in (0,1)$, ${\parallel f-h,g-h\parallel }_{\alpha }$ is called an area of f, g and h. We call Ψ a 2-isometry if ${\parallel f-h,g-h\parallel }_{\alpha }={\parallel \mathrm{\Psi }(f)-\mathrm{\Psi }(h),\mathrm{\Psi }(g)-\mathrm{\Psi }(h)\parallel }_{\beta }$ for all $f,g,h\in \mathrm{\Im }(X)$ and $\alpha ,\beta \in (0,1)$.

A version of the Mazur-Ulam theorem has been obtained in [25] as follows.

Theorem 3.1 [25]

Assume that $\mathrm{\Im }(X)$ and $\mathrm{\Im }(Y)$ are fuzzy 2-normed linear spaces. If $\mathrm{\Psi }:\mathrm{\Im }(X)\to \mathrm{\Im }(Y)$ is a 2-isometry and satisfies $\mathrm{\Psi }(f)$, $\mathrm{\Psi }(g)$ and $\mathrm{\Psi }(h)$ are collinear when f, g and h are collinear, then Ψ is affine.

A natural question is whether the 2-isometry in the fuzzy 2-normed linear spaces is also affine without the condition of preserving collinearity. In this section, we find a reply to this question when X is a 2-fuzzy 2-normed linear space or $\mathrm{\Im }(X)$ is a fuzzy 2-normed linear space.

Lemma 3.1 [25]

For all $f,g\in \mathrm{\Im }(X)$, $\alpha \in (0,1)$ and $\lambda \in \mathbb{R}$. Then

$${\parallel f,g\parallel }_{\alpha }={\parallel f,g+\lambda f\parallel }_{\alpha }.$$

Lemma 3.2 Let $f,g,h\in \mathrm{\Im }(X)$ and $\alpha \in (0,1)$. Then $v=\frac{f+g}{2}$ is the unique element of $\mathrm{\Im }(X)$ satisfying

$${\parallel f-h,f-v\parallel }_{\alpha }={\parallel g-v,g-h\parallel }_{\alpha }=\frac{1}{2}{\parallel f-h,g-h\parallel }_{\alpha }$$

with ${\parallel f-h,g-h\parallel }_{\alpha }\ne 0$ and $v\in \{kf+(1-k)g:k\in \mathbb{R}\}$.

Proof From Lemma 3.1, it is obvious that $v=\frac{f+g}{2}$ satisfies

$${\parallel f-h,f-v\parallel }_{\alpha }={\parallel g-v,g-h\parallel }_{\alpha }=\frac{1}{2}{\parallel f-h,g-h\parallel }_{\alpha }$$

with ${\parallel f-h,g-h\parallel }_{\alpha }\ne 0$ and $v\in \{kf+(1-k)g:k\in \mathbb{R}\}$.

For the uniqueness of v, assume that $u\in \mathrm{\Im }(X)$ also satisfies

$${\parallel f-h,f-u\parallel }_{\alpha }={\parallel g-u,g-h\parallel }_{\alpha }=\frac{1}{2}{\parallel f-h,g-h\parallel }_{\alpha }$$

with ${\parallel f-h,g-h\parallel }_{\alpha }\ne 0$ and $u\in \{kf+(1-k)g:k\in \mathbb{R}\}$. Let $u=kf+(1-k)g$ for some $k\in \mathbb{R}$. From Lemma 3.1, we have

$$\begin{array}{rcl}{\parallel f-h,g-h\parallel }_{\alpha }& =& 2{\parallel f-h,f-u\parallel }_{\alpha }\\ =& 2{\parallel f-h,f-(kf+(1-k)g)\parallel }_{\alpha }\\ =& 2|1-k|{\parallel f-h,f-g\parallel }_{\alpha }\\ =& 2|1-k|{\parallel f-h,g-h\parallel }_{\alpha }\end{array}$$

and

$$\begin{array}{rcl}{\parallel f-h,g-h\parallel }_{\alpha }& =& 2{\parallel g-h,g-u\parallel }_{\alpha }\\ =& 2{\parallel g-h,g-(kf+(1-k)g)\parallel }_{\alpha }\\ =& 2|k|{\parallel g-h,g-f\parallel }_{\alpha }\\ =& 2|k|{\parallel f-h,g-h\parallel }_{\alpha }.\end{array}$$

Since ${\parallel f-h,g-h\parallel }_{\alpha }\ne 0$, we have $1=2|1-k|=2|k|$. So, $k=\frac{1}{2}$ and $u=v=\frac{f+g}{2}$. □

Theorem 3.2 Let $\mathrm{\Im }(X)$ and $\mathrm{\Im }(Y)$ be fuzzy 2-normed linear spaces. If $\mathrm{\Psi }:\mathrm{\Im }(X)\to \mathrm{\Im }(Y)$ is a 2-isometry, then Ψ is affine.

Proof Let $\mathrm{\Phi }(f)=\mathrm{\Psi }(f)-\mathrm{\Psi }(0)$. Obviously, $\mathrm{\Phi }(0)=0$ and Φ is a 2-isometry. Now, we prove that Φ is linear.

Firstly, we show that Φ is additive. For $f,g,h\in \mathrm{\Im }(X)$, $\alpha ,\beta \in (0,1)$ with ${\parallel f-h,g-h\parallel }_{\alpha }\ne 0$, ${\parallel \mathrm{\Phi }(f)-\mathrm{\Phi }(h),\mathrm{\Phi }(g)-\mathrm{\Phi }(h)\parallel }_{\beta }\ne 0$ and from Lemma 3.1, we have

$$\begin{array}{rcl}{\parallel \mathrm{\Phi }(f)-\mathrm{\Phi }(h),\mathrm{\Phi }(f)-\mathrm{\Phi }\left(\frac{f+g}{2}\right)\parallel }_{\beta }& =& {\parallel f-h,f-\frac{f+g}{2}\parallel }_{\alpha }\\ =& {\parallel f-h,\frac{f-g}{2}\parallel }_{\alpha }\\ =& \frac{1}{2}{\parallel f-h,f-g\parallel }_{\alpha }\\ =& \frac{1}{2}{\parallel f-h,g-h\parallel }_{\alpha }\\ =& \frac{1}{2}{\parallel \mathrm{\Phi }(f)-\mathrm{\Phi }(h),\mathrm{\Phi }(g)-\mathrm{\Phi }(h)\parallel }_{\beta }.\end{array}$$

Similarly,

$${\parallel \mathrm{\Phi }(g)-\mathrm{\Phi }(h),\mathrm{\Phi }(g)-\mathrm{\Phi }\left(\frac{f+g}{2}\right)\parallel }_{\beta }=\frac{1}{2}{\parallel \mathrm{\Phi }(f)-\mathrm{\Phi }(h),\mathrm{\Phi }(g)-\mathrm{\Phi }(h)\parallel }_{\beta }.$$

And

$$\begin{array}{rcl}{\parallel \mathrm{\Phi }\left(\frac{f+g}{2}\right)-\mathrm{\Phi }(g),\mathrm{\Phi }(f)-\mathrm{\Phi }(g)\parallel }_{\beta }& =& {\parallel \frac{f+g}{2}-g,f-g\parallel }_{\alpha }\\ =& \frac{1}{2}{\parallel f-g,f-g\parallel }_{\alpha }=0.\end{array}$$

So, we get

$$\mathrm{\Phi }\left(\frac{f+g}{2}\right)-\mathrm{\Phi }(g)=k(\mathrm{\Phi }(f)-\mathrm{\Phi }(g))$$

for some $k\in \mathbb{R}$ by Definition 2.7. That is,

$$\mathrm{\Phi }\left(\frac{f+g}{2}\right)=k\mathrm{\Phi }(f)+(1-k)\mathrm{\Phi }(g).$$

Thus, from Lemma 3.2,

$$\mathrm{\Phi }\left(\frac{f+g}{2}\right)=\frac{\mathrm{\Phi }(f)+\mathrm{\Phi }(g)}{2}$$

for all $f,g\in \mathrm{\Im }(X)$.

Since $\mathrm{\Phi }(0)=0$, we have

$$\mathrm{\Phi }\left(\frac{f}{2}\right)=\mathrm{\Phi }\left(\frac{f+0}{2}\right)=\frac{\mathrm{\Phi }(f)+\mathrm{\Phi }(0)}{2}=\frac{\mathrm{\Phi }(f)}{2}$$

and

$$\begin{array}{rcl}\mathrm{\Phi }(f+g)& =& \mathrm{\Phi }\left(\frac{2f+2g}{2}\right)=\frac{\mathrm{\Phi }(2f)+\mathrm{\Phi }(2g)}{2}=\frac{\mathrm{\Phi }(2f)}{2}+\frac{\mathrm{\Phi }(2g)}{2}\\ =& \mathrm{\Phi }(f)+\mathrm{\Phi }(g).\end{array}$$

It follows that Φ is additive.

Secondly, we show that $\mathrm{\Phi }(rf)=r\mathrm{\Phi }(f)$ for every $r\in \mathbb{R}$, $f\in \mathrm{\Im }(X)$ and $\alpha ,\beta \in (0,1)$. Let $r\in {\mathbb{R}}^{+}$ and $f\in \mathrm{\Im }(X)$ and $\alpha ,\beta \in (0,1)$. Since $\mathrm{\Phi }(0)=0$ and Φ is a 2-isometry, we have

$$\begin{array}{rcl}{\parallel \mathrm{\Phi }(rf),\mathrm{\Phi }(f)\parallel }_{\beta }& =& {\parallel \mathrm{\Phi }(rf)-\mathrm{\Phi }(0),\mathrm{\Phi }(f)-\mathrm{\Phi }(0)\parallel }_{\beta }\\ =& {\parallel rf-0,f-0\parallel }_{\alpha }\\ =& {\parallel rf,f\parallel }_{\alpha }\\ =& 0.\end{array}$$

So, $\mathrm{\Phi }(rf)=s\mathrm{\Phi }(f)$ for some $s\in \mathbb{R}$ from Definition 2.7. As $dim\mathrm{\Im }(X)>1$, there exists a $g\in \mathrm{\Im }(X)$ such that ${\parallel f,g\parallel }_{\alpha }\ne 0$. It is easy to see that

$$\begin{array}{rcl}r{\parallel f,g\parallel }_{\alpha }& =& {\parallel rf,g\parallel }_{\alpha }={\parallel \mathrm{\Phi }(rf),\mathrm{\Phi }(g)\parallel }_{\beta }={\parallel s\mathrm{\Phi }(f),\mathrm{\Phi }(g)\parallel }_{\beta }\\ =& |s|{\parallel \mathrm{\Phi }(f),\mathrm{\Phi }(g)\parallel }_{\beta }=|s|{\parallel f,g\parallel }_{\alpha }.\end{array}$$

So, $s=r$ or $s=-r$. If $s=-r$, then

$$\begin{array}{rcl}|r-1|{\parallel f,g\parallel }_{\alpha }& =& {\parallel (r-1)f,g\parallel }_{\alpha }={\parallel rf-f,g-0\parallel }_{\alpha }\\ =& {\parallel \mathrm{\Phi }(rf)-\mathrm{\Phi }(f),\mathrm{\Phi }(g)-\mathrm{\Phi }(0)\parallel }_{\beta }\\ =& {\parallel -r\mathrm{\Phi }(f)-\mathrm{\Phi }(f),\mathrm{\Phi }(g)\parallel }_{\beta }\\ =& (r+1){\parallel \mathrm{\Phi }(f),\mathrm{\Phi }(g)\parallel }_{\beta }\\ =& (r+1){\parallel f,g\parallel }_{\alpha }.\end{array}$$

So, $|r-1|=r+1$. This is a contradiction since $r\in {\mathbb{R}}^{+}$. Thus, $\mathrm{\Phi }(rf)=r\mathrm{\Phi }(f)$ for every $r\in {\mathbb{R}}^{+}$, $f\in \mathrm{\Im }(X)$ and $\alpha ,\beta \in (0,1)$.

Similarly, we can prove $\mathrm{\Phi }(rf)=r\mathrm{\Phi }(f)$ for every $r\in {\mathbb{R}}^{-}$, $f\in \mathrm{\Im }(X)$ and $\alpha ,\beta \in (0,1)$.

Hence, we prove that Φ is linear and Ψ is affine. □

Remark 3.1 Theorem 3.1 has been substantially improved by Theorem 3.2.

Remark 3.2 It is clear that the Mazur-Ulam theorem has been proved under much weaker conditions than the main result of Alaca [25] in the framework of 2-fuzzy 2-normed linear spaces.

Open problem How can obtain some results for the Aleksandrov problem in fuzzy 2-normed linear spaces with the help of this technique?