- Research
- Open access
- Published:
On coupled fixed point results in asymmetric G-metric spaces
Journal of Inequalities and Applications volume 2013, Article number: 528 (2013)
Abstract
Using a combination of techniques introduced by Jleli and Samet (Fixed Point Theory Appl. 2012:210, 2012) and Samet et al. (Int. J. Anal. 2013:917158, 2013) on the one hand, and by Kadelburg et al. (Bull. Math. Anal. Appl. 4:51-63, 2012) on the other hand, we show that several coupled fixed point results in (ordered) G-metric spaces obtained recently are simple consequences of the respective standard (ordered) metric results. The technique can be applied both in symmetric and asymmetric cases. Moreover, we show by an example that the results thus obtained are usually stronger than those presented in the literature.
MSC:47H10, 54H25.
1 Introduction
As one of fruitful generalizations of metric spaces, G-metric spaces were introduced by Mustafa and Sims in [1]. In several subsequent papers, these and other authors obtained many fixed point and common fixed point results, thus extending the known theory from the standard metric case. It should be noted that there exist two kinds of G-metric spaces, symmetric and asymmetric ones, and while it was immediately clear that in the symmetric case these results can be easily reduced to their metric counterparts, in the asymmetric case, new proofs usually had to be found.
The notion of a coupled fixed point for mappings with two variables was introduced in the articles [2–4]. After that, a great number of mathematicians worked in this field and obtained a lot of results in metric and various abstract metric spaces (see, e.g., [5–10]). Coupled fixed points in G-metric spaces were investigated, e.g., in the papers [11–23].
Very recently, some new methods were presented for obtaining fixed point and coupled fixed point results. On the one hand, Jleli and Samet [24] and Samet et al. [25] showed that there is a very simple technique for reducing fixed point results in G-metric spaces, both in symmetric and in asymmetric cases, to their metric counterparts, avoiding complicated proofs from the known papers. On the other hand, in the papers [26–33], the authors presented another technique which reduces coupled fixed point results in metric and various abstract metric spaces to the results for mappings with one variable. This technique was used by Kadelburg et al. [34] and afterwards by Agarwal and Karapinar [35] to obtain coupled fixed point results in symmetric G-metric spaces.
By combining the mentioned techniques, we show in this paper that several coupled fixed point results in (ordered) G-metric spaces obtained in recent years and presented in the papers [11–23] simply follow from the well-known standard (ordered) metric results for mappings with one variable. The technique can be applied in both symmetric and asymmetric cases. Moreover, we will show by an example that the results obtained in this way are usually stronger and can be applied in a greater number of cases.
2 Preliminaries
For more details on the following definitions and results concerning G-metric spaces, we refer the reader to [1].
Definition 1 Let 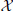 be a nonempty set, and let be a function satisfying the following properties:
be a nonempty set, and let be a function satisfying the following properties:
(G1) if ;
(G2) for all with ;
(G3) for all with ;
(G4) (symmetry in all three variables);
(G5) for all (rectangle inequality).
Then the function g is called a G-metric on 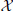 and the pair is called a G-metric space.
and the pair is called a G-metric space.
Definition 2 Let be a G-metric space, and let be a sequence of points in 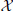 .
.
-
1.
A point is said to be the limit of a sequence if , and one says that the sequence is g-convergent to x.
-
2.
The sequence is said to be a G-Cauchy sequence if, for every , there is a positive integer N such that for all ; that is, if as .
-
3.
is said to be G-complete (or a complete G-metric space) if every G-Cauchy sequence in is G-convergent in
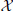 .
.
It was shown in [1] that a G-metric induces a Hausdorff topology and that the convergence, as described in the above definition, is relative to this topology. The topology being Hausdorff, a sequence can converge to at most one point.
Definition 3 A G-metric space is called symmetric if
holds for all .
The following are some simple examples of G-metric spaces.
Example 1 (1) Let be an ordinary metric space. Define g by
for all . Then it is clear that is a symmetric G-metric space.
(2) Let . Define
and extend g to by using the symmetry in the variables. Then it is clear that is an asymmetric G-metric space.
Remark 1 If is a G-metric space, then
defines a standard metric on 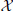 . If the G-metric g is symmetric, this reduces to . This simple fact implies that most of the fixed point results in symmetric G-metric spaces can be easily reduced to their metric counterparts. In the asymmetric case, another approach is needed.
. If the G-metric g is symmetric, this reduces to . This simple fact implies that most of the fixed point results in symmetric G-metric spaces can be easily reduced to their metric counterparts. In the asymmetric case, another approach is needed.
Let be a partially ordered set, and .
-
1.
f is said to have the h-mixed monotone property if the following two conditions are satisfied:
If (the identity map), we say that f has the mixed monotone property.
-
2.
A point is said to be a coupled coincidence point of f and h if and , and their common coupled fixed point if and .
-
3.
The mappings f and h are called w-compatible if and whenever and .
If 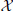 is a nonempty set, then the triple is called an ordered G-metric space if:
is a nonempty set, then the triple is called an ordered G-metric space if:
-
(i)
is a G-metric space, and
-
(ii)
is a partially ordered set.
3 Main results
We will use the following simple lemma for obtaining our results.
Lemma 1 Let be an ordered G-metric space.
-
(a)
If a relation ⊑ is defined on by
and mappings and are given by
for , then and are ordered G-metric spaces. The spaces and are complete iff is complete.
-
(b)
If is a self-map, and a mapping has the h-mixed monotone property, then the mapping given by
is H-nondecreasing w.r.t. ⊑, i.e.,
where is defined by .
-
(c)
If h is continuous in , then H is continuous in both and . If f is continuous from to (resp. from to ), then F is continuous in (resp. in ).
Proof We will only check the second part of assertion (a); the proofs of all other parts are straightforward.
It was stated already in [1] that if g is a G-metric on 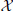 , then
, then
define standard metrics on 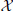 , and that topologies thus generated are the same as the topology of . In particular, the completeness is satisfied simultaneously.
, and that topologies thus generated are the same as the topology of . In particular, the completeness is satisfied simultaneously.
On the other hand, it is well known that for each (standard) metric space , the mappings
for are metrics on , also preserving the completeness property. Combining these two facts, we obtain that the mappings
satisfy all the stated properties. □
Remark 2 If the given G-metric space is symmetric, then, using the construction given in [[34], Lemma 3.1] and afterwards in [[35], Sections 4 and 5], we can obtain the previous result in a slightly different way. Namely, in this case, one can consider the G-metric G on given by
and then associate the metrics
It is easy to see that, in fact, and .
However, this approach cannot be used in the asymmetric case, since in this case, (3.1) does not define a G-metric on (see [[1], Section 4] and, further, Example 2).
Now we are ready to state some of our main results. We start, as a sample, with the following theorem.
Theorem 1 Let be a complete partially ordered G-metric space, and let and be mappings such that , is closed and f has the mixed h-monotone property. Suppose that there exist such that and . Suppose also that there exists such that
for all satisfying ( and ) or ( and ). Let us assume also that if is a nondecreasing sequence in 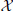 converging to some , then for each . Then the mappings f and h have a coupled coincidence point. Moreover, if f and h are w-compatible, then f and h have a common coupled fixed point.
converging to some , then for each . Then the mappings f and h have a coupled coincidence point. Moreover, if f and h are w-compatible, then f and h have a common coupled fixed point.
Proof Consider the complete partially ordered metric space and the mappings and defined in Lemma 1. Then, obviously, the following conditions hold:
-
1.
and is closed;
-
2.
F is H-nondecreasing;
-
3.
There exists such that .
Moreover, it follows from (3.2) that there exists such that
holds for all such that or . Now, all the conditions of a special case of [[37], Theorem 2.2] are fulfilled and it follows that the mappings F and H have a coincidence point which is, obviously, a coupled coincidence point of f and h. The last assertion also follows easily. □
Corollary 1 Let be a complete partially ordered G-metric space, and let and be mappings such that , is closed and f has the mixed h-monotone property. Suppose that there exist such that and . Suppose also that there exists such that
for all satisfying ( and ) or ( and ). Let us assume also that if is a nondecreasing sequence in 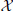 converging to some , then for each . Then the mappings f and h have a coupled coincidence point. Moreover, if f and h are w-compatible, then f and h have a common coupled fixed point.
converging to some , then for each . Then the mappings f and h have a coupled coincidence point. Moreover, if f and h are w-compatible, then f and h have a common coupled fixed point.
Proof We have only to prove that condition (3.4) implies condition (3.2). Indeed, putting and in (3.4), we get that
and putting and , we get
Adding up, and taking into account the definitions of mappings F and H as well as the definition of metric , we obtain condition (3.2) (i.e., condition (3.3)). □
In an even easier way, one can obtain the following versions of the previous results in the space without order. In this case, the given technique reduces the problem simply to the Banach contraction principle.
Theorem 2 Let be a complete G-metric space, and let and be mappings such that and is closed. Suppose also that there exists such that condition (3.2) holds for all . If h is continuous, then the mappings f and h have a coupled coincidence point. Moreover, if f and h are w-compatible, then f and h have a common coupled fixed point.
Corollary 2 Let be a complete G-metric space, and let and be mappings such that and is closed. Suppose also that there exists such that condition (3.4) holds for all . If h is continuous, then the mappings f and h have a coupled coincidence point. Moreover, if f and h are w-compatible, then f and h have a common coupled fixed point.
Remark 3 The last result was obtained (in the special case ) in [[34], Corollary 4.1] and afterwards (implicitly) in the course of proof of [[35], Theorem 5.3], but in the case when the given G-metric g is symmetric. The proof from these articles cannot be applied in the asymmetric case (see Remark 2 and, further, Example 2).
Remark 4 The obtained results are strict improvements of some results obtained earlier. In the symmetric case, this was shown by Kadelburg et al. (see [[34], Example 4.1]). We present an example in an asymmetric case.
Example 2 Let be the G-metric space considered in [[38], Example 3.4], i.e., let and be given as
and extended by symmetry in the variables. Then it is easy to check that g is a G-metric which is asymmetric since and .
Let be given as , and let be defined by
We will show first that f and h satisfy neither the condition
for any (which is condition (3.1) from [15]) nor (weaker) condition (3.4). Indeed, take, e.g., and and condition (3.4) becomes
which is a contradiction for any . Hence, neither [[15], Theorem 3.1] nor Corollary 2 can be used to conclude that f and h have a coupled coincidence point (i.e., that f has a coupled fixed point).
In order to show that f and h satisfy the conditions of Theorem 2, we first note that , and
Take now . By a careful calculation (there are 21 nontrivial cases) it can be checked that condition (3.2) (i.e., condition (3.3)) is satisfied for all .
Hence, Theorem 2 can be applied to conclude that f has a coupled fixed point (which is ).
We note also that the approach from the papers [34, 35] cannot be used in this example since
does not define a G-metric on . Indeed, e.g.,
although , and the property (G3) of G-metrics is not satisfied.
For the sake of simplicity, we shall consider in the rest of the paper ‘unordered’ versions of coupled fixed point results. ‘Ordered’ versions can be formulated and proved using usual variations.
The proof of our next result uses the metric .
Theorem 3 Let be a complete G-metric space, and let . Suppose that there exists such that for all the following inequality holds:
Then f has a unique coupled fixed point in and it is of the form for some .
Proof Consider the complete metric space and the mapping defined in Lemma 1. Putting and in (3.5), one gets
interchanging the places of x and y, as well as of s and t, this gives
Putting now and in (3.5), one gets
interchanging the places of x and y, as well as of s and t, this gives
Taking into account the definition of metric in Lemma 1, it follows from the last four inequalities that
holds for all . By a well-known result from the theory of standard metric spaces (see, e.g., [39]), it follows that there exists a unique point such that . Obviously, is a coupled fixed point of the mapping f. Since the coupled fixed point is unique, it must be of the form for some . □
When considering situations where contractive conditions are of ‘weak’ kind, or they use the so-called comparison functions, a variation of the previous approach is needed. One possibility is to use quasi-metrics. Recall that a pair is called a quasi-metric space if the mapping d has all the properties of a metric except, possibly, the symmetry . For some properties of quasi-metric spaces, we refer to [24]. In particular, the following fixed point result was proved in that paper.
Theorem 4 [[24], Theorem 3.2]
Let be a complete quasi-metric space, and let be a mapping satisfying
for all , where is continuous with . Then T has a unique fixed point.
Remark 5 An additional nondecreasing function ψ could be added in (3.6) to become
However, it was shown in [40] that it is redundant, hence we will not use it here.
Obviously, if is a G-metric space, then
defines a quasi-metric on 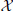 . Moreover,
. Moreover,
defines a quasi-metric on . The space is complete iff is G-complete. Now we can easily prove the following theorem.
Theorem 5 Let be a complete G-metric space, and let satisfy
for all , where is continuous with . Then f has a unique coupled fixed point.
Proof Consider the (complete) quasi-metric space given by (3.7) and the self-mapping F given on by for . Then contractive condition (3.8) gives
for . Hence, Theorem 4 can be applied to conclude that F has a unique fixed point, which is then a coupled fixed point of f. □
Another possibility is to impose an additional condition on the function φ, or on the comparison function Φ. This is illustrated in the next result.
Theorem 6 Let be a complete G-metric space, and let satisfy the condition
for all , where is right-continuous, for and for . Then f has a unique coupled fixed point.
Proof Consider again the space and the mapping F given in Lemma 1. Putting and in (3.9), we get
interchanging places of x and y, as well as s and t, we obtain
On the other hand, putting and in (3.9), we get
interchanging places of x and y, as well as s and t, we obtain
Adding up the last four inequalities, and using the assumed properties of function Φ, we get that
for all . Hence, by a classical result of Boyd and Wong [41], it follows that F has a unique fixed point, which is then a coupled fixed point of f. □
It is clear that a lot of other known coupled fixed point results in G-metric spaces (both symmetric and asymmetric) can be easily obtained in this way.
References
Mustafa Z, Sims B: A new approach to generalized metric spaces. J. Nonlinear Convex Anal. 2006, 7(2):289–297.
Guo D, Lakshmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Anal. 1987, 11: 623–632. 10.1016/0362-546X(87)90077-0
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Lakshmikantham V, Ćirić L: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal. 2009, 70: 4341–4349. 10.1016/j.na.2008.09.020
Sintunavarat W, Cho YJ, Kumam P: Coupled coincidence point theorems for contractions without commutative condition in intuitionistic fuzzy normed spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 81
Sintunavarat W, Cho YJ, Kumam P: Coupled fixed point theorems for weak contraction mapping under F -invariant set. Abstr. Appl. Anal. 2012., 2012: Article ID 324874
Sintunavarat W, Cho YJ, Kumam P: Coupled fixed point theorem for contraction mapping induced by cone ball-metric in partially ordered spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 128
Sintunavarat W, Petruşel A, Kumam P:Common coupled fixed point theorems for -compatible mappings without mixed monotone property. Rend. Circ. Mat. Palermo 2012, 61: 361–382. 10.1007/s12215-012-0096-0
Sintunavarat W, Kumam P, Cho YJ: Coupled fixed point theorems for nonlinear contractions without mixed monotone property. Fixed Point Theory Appl. 2012., 2012: Article ID 170
Karapınar E, Kumam P, Sintunavarat W: Coupled fixed point theorems in cone metric spaces with a c -distance and applications. Fixed Point Theory Appl. 2012., 2012: Article ID 194
Abbas M, Sintunavarat W, Kumam P: Coupled fixed point of generalized contractive mappings on partially ordered G -metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 31
Aydi H, Damjanović B, Samet B, Shatanawi W: Coupled fixed point theorems for nonlinear contractions in partially ordered G -metric spaces. Math. Comput. Model. 2011, 54: 2443–2450. 10.1016/j.mcm.2011.05.059
Aydi H, Postolache M, Shatanawi W: Coupled fixed point results for -weakly contractive mappings in ordered G -metric spaces. Comput. Math. Appl. 2012, 63: 298–309. 10.1016/j.camwa.2011.11.022
Cho YJ, Rhoades BE, Saadati R, Samet B, Shatanawi W: Nonlinear coupled fixed point theorems in ordered generalized metric spaces with integral type. Fixed Point Theory Appl. 2012., 2012: Article ID 8
Choudhury BS, Maity P: Coupled fixed point results in generalized metric spaces. Math. Comput. Model. 2011, 54: 73–79. 10.1016/j.mcm.2011.01.036
Karapinar E, Kaymakcalan B, Taş K: On coupled fixed point theorems on partially ordered G -metric spaces. J. Inequal. Appl. 2012., 2012: Article ID 200
Karapinar E, Kumam P, Erhan IM: Coupled fixed points on partially ordered G -metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 174
Luong NV, Thuan NX: Coupled fixed point theorems in partially ordered G -metric space. Math. Comput. Model. 2012, 55: 1601–1609. 10.1016/j.mcm.2011.10.058
Mohiuddine SM, Alotaibi A: On coupled fixed point theorems for nonlinear contractions in partially ordered G -metric spaces. Abstr. Appl. Anal. 2012., 2012: Article ID 897198
Nashine HK: Coupled common fixed point results in ordered G -metric spaces. J. Nonlinear Sci. Appl. 2012, 1: 1–13.
Shatanawi W: Coupled fixed point theorems in generalized metric spaces. Hacet. J. Math. Stat. 2011, 40: 441–447.
Shatanawi W, Abbas M, Nazir T: Common coupled coincidence and coupled fixed point results in two generalized metric space. Fixed Point Theory Appl. 2011., 2011: Article ID 80
Wangkeeree R: Coupled fixed point theorems for generalized contractive mappings in partially ordered G -metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 172
Jleli M, Samet B: Remarks on G -metric spaces and fixed point theorems. Fixed Point Theory Appl. 2012., 2012: Article ID 210
Samet B, Vetro C, Vetro F: Remarks on G -metric spaces. Int. J. Anal. 2013., 2013: Article ID 917158
Amini-Harandi A: Coupled and tripled fixed point theory in partially ordered metric spaces with application to initial value problem. Math. Comput. Model. 2013, 57: 2343–2348. 10.1016/j.mcm.2011.12.006
Berinde V: Generalized coupled fixed point theorems for mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 2011, 74: 7347–7355. 10.1016/j.na.2011.07.053
Berinde V: Coupled fixed point theorems for ϕ -contractive mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 2012, 75: 3218–3228. 10.1016/j.na.2011.12.021
Berinde V: Coupled coincidence point theorems for mixed monotone nonlinear operators. Comput. Math. Appl. 2012, 64: 1770–1777. 10.1016/j.camwa.2012.02.012
Golubović Z, Kadelburg Z, Radenović S: Coupled coincidence points of mappings in ordered partial metric spaces. Abstr. Appl. Anal. 2012., 2012: Article ID 192581
Kadelburg Z, Radenović S: Coupled fixed point results under tvs-cone metric and w -cone-distance. Adv. Fixed Point Theory 2012, 2: 29–46.
Jleli M, Rajić VĆ, Samet B, Vetro C: Fixed point theorems on ordered metric spaces and applications to nonlinear elastic beam equations. J. Fixed Point Theory Appl. 2012, 12: 175–192. 10.1007/s11784-012-0081-4
Kadelburg Z, Nashine HK, Radenović S: Coupled fixed point results in 0-complete ordered partial metric spaces. J. Adv. Math. Stud. 2013, 6: 159–172.
Kadelburg Z, Nashine HK, Radenović S: Common coupled fixed point results in partially ordered G -metric spaces. Bull. Math. Anal. Appl. 2012, 4: 51–63.
Agarwal RP, Karapinar E: Remarks on some coupled fixed point theorems in G -metric spaces. Fixed Point Theory Appl. 2013., 2013: Article ID 2
Abbas M, Ilić D, Khan MA: Coupled coincidence point and coupled common fixed point theorems in partially ordered metric spaces with w -distance. Fixed Point Theory Appl. 2010., 2010: Article ID 134897
Ćirić LB, Cakić N, Rajović M, Ume JS: Monotone generalized nonlinear contractions in partially ordered metric spaces. Fixed Point Theory Appl. 2008., 2008: Article ID 131294
Nashine, HK, Kadelburg, Z, Radenović, S: Coincidence and fixed point results under generalized weakly contractive condition in partially ordered G-metric spaces. Filomat (to appear)
Ćirić LB: A generalization of Banach’s contraction principle. Proc. Am. Math. Soc. 1974, 45: 267–273.
Jachymski J: Equivalent conditions for generalized contractions on (ordered) metric spaces. Nonlinear Anal. 2011, 74: 768–774. 10.1016/j.na.2010.09.025
Boyd DW, Wong JS: On nonlinear contractions. Proc. Am. Math. Soc. 1969, 20: 458–464. 10.1090/S0002-9939-1969-0239559-9
Acknowledgements
The authors are indebted to the referees whose suggestions helped them to improve the exposition. The second and third authors are thankful to the Ministry of Education, Science and Technological Development of Serbia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R.P., Kadelburg, Z. & Radenović, S. On coupled fixed point results in asymmetric G-metric spaces. J Inequal Appl 2013, 528 (2013). https://doi.org/10.1186/1029-242X-2013-528
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-528