- Research
- Open access
- Published:
Estimates of the approximation of weighted sums of conditionally independent random variables by the normal law
Journal of Inequalities and Applications volume 2013, Article number: 320 (2013)
Abstract
A Berry-Esseen-like inequality is provided for the difference between the characteristic function of a weighted sum of conditionally independent random variables and the characteristic function of the standard normal law. Some applications and possible extensions of the main result are also illustrated.
MSC:60F05, 60G50.
1 Introduction and main result
Berry-Esseen inequalities are currently considered, within the realm of the central limit problem of probability theory, as a powerful tool to evaluate the error in approximating the law of a standardized sum of independent random variables (r.v.’s) by the normal distribution. The classical version of the statement at issue is due, independently, to Berry [1] and to Esseen [2], and it is condensed into the well-known inequality
valid for a given a sequence of non-degenerate, independent and identically distributed (i.i.d.) real-valued r.v.’s such that . Here, C is a universal constant, stands for the variance and , G denote the distribution functions
respectively. The proof of (1) is based on the evaluation of an upper bound for the modulus of the difference between the characteristic function (c.f.) and the c.f. of the standard normal distribution. See, for example, Theorems 1-2 in Chapter 5 of [3]. In fact, under the above hypotheses on , one can prove that
holds for every , while an analogous estimate for the first two derivatives can be also obtained with a bit of work, namely
for all and , C being another suitable constant. As a reference for (2)-(3), see, e.g., Lemma 1 in Chapter 5 and Lemma 4 in Chapter 6 of [3], respectively.
Due to a significant and constantly updating employment of Berry-Esseen-like inequalities in different areas of pure and applied mathematics - such as stochastic processes, mathematical statistics, Markov chain Monte Carlo, random graphs, combinatorics, coding theory and kinetic theory of gases - the researchers have tried to continuously generalize this kind of estimates. Confining ourselves to the case of a limiting distribution coinciding with the standard normal law, the main lines of research can be summarized as follows: (1) Taking account of different kinds of stochastic dependence - typically, less restrictive than the i.i.d. setting - such as the case of sequences of independent, non-identically distributed r.v.’s (see Chapters 5-6 of [3] and the recent papers [4–6]), martingales [7], exchangeable r.v.’s [8] and Markov processes [9]. (2) Evaluation of the discrepancy between and G by means of probability metrics different from the Kolmogorov distance, i.e., the LHS of (1). Classical references are Chapters 5-6 of [10], Chapters 5-6 of [3] and Chapters 3-5 of [11], while a more recent treatment is contained in [12]. Strong metrics, such as total variation or entropy metrics, are dealt with in [13–17]. (3) Formulation of different hypotheses about the moments, both in the direction of weakening (i.e., considering moments of order , with ) or sharpening (i.e., considering the k th moments with ) the initial assumption . The above-mentioned references are comprehensive also of this kind of variants.
The present paper contains some generalizations of the Berry-Esseen estimate, which fall within the three aforementioned lines of research, by starting from the main statement (Theorem 1 below) reminiscent of inequalities (2)-(3). To present the main result in a framework as general as possible, we consider a weighted sum of the form
where the ’s are constants satisfying
and the ’s are conditionally independent r.v.’s, possibly non-identically distributed. To formalize this point, we assume that there exist a probability space and a sub-σ-algebra ℋ of ℱ such that
holds almost surely (a.s.) for any in the Borel class . We also assume that
holds a.s. for , and that
is in force. Then, after putting and defining the entities
we state our main result.
Theorem 1 Under assumptions (5)-(8) one has
for every t in and , where , , , are rapidly decreasing continuous functions, which can be put into the form with and explicitly.
The general setting of this theorem is suitable to treat a vast number of standard cases. For example, in the simplest situation of a sequence of i.i.d. r.v.’s with , and , one can put to get a.s. and, consequently, . Whence,
holds for all t such that and . Therefore, after noting that and have a standard form with , a plain application of Theorems 1-2 in Chapter 5 of [3] leads to an inequality of the type of (1), with a rate of convergence to zero proportional to and , provided that these two quantities go to zero when n diverges. Moreover, when the additional hypothesis , for , is in force with some (to be compared with (14) in [5]), it is possible to deduce a bound for the normal approximation w.r.t. the total variation distance, by following the argument developed in [18]. Indeed, starting from Proposition 4.1 therein (Beurling’s inequality), one can write
with a suitable constant C. Then, one can bound the RHS from above exactly as in Section 4 of the quoted paper. In general, it should be noticed that (9) reduces to a more standard inequality with Y and W only, whenever the ’s are properly scaled w.r.t. conditional variances (i.e., when holds a.s. for ). In the less trivial case of independent, non-identically distributed r.v.’s, with for and , one can take again to show that the normalization of w.r.t. variance reduces to a.s. Since ensues from this condition, the RHS of (9) assumes again a nice form with X, Y and W only. Now, we do not linger further on these standard applications of (9), since we deem more convenient to stress the role of the unusual terms like , X and Z, and to comment on the utility of formulating Theorem 1 in the general framework of conditionally independent r.v.’s, which, being a novelty in this study, has motivated the drafting of this paper. As an illustrative example, we consider, on , a sequence of independent r.v.’s and a random function , taking values in some subset ℱ of the space of all measurable, uniformly bounded functions (i.e., for which there exists such that for all and ), which is stochastically independent of X. Putting for all and , and assuming that for all and , we have that (6)-(8) are fulfilled. At this stage, it is worth recalling that a number of problems in pure and applied statistics, such as filtering and reproducing kernel Hilbert space estimates, can be formulated within this framework and would be greatly enhanced by the knowledge of the error in approximating the law of the sum by the normal distribution. See [19], and also [20] for a Bayesian viewpoint. Then Theorem 1 entails the following corollary.
Corollary 2 Suppose that converges to zero as n diverges, where and is a suitable probability measure satisfying . Suppose further that converges to zero as n diverges, where and are two independent copies of . If
satisfies for , then there is a constant C such that
is valid for all .
To conclude the presentation of the main result, we will deal with three other applications, specifically to exchangeable sequences of r.v.’s, to mixtures of Markov chains and to the homogeneous Boltzmann equation. Due to the technical nature of these applications, we have deemed more convenient to isolate each of them into a respective subsection, labeled Subsections 1.1, 1.2 and 1.3, respectively. Section 2 is dedicated to the proof of Theorem 1, which contains also an explicit characterization of the functions ’s and ’s, and to the proof of Corollary 2.
1.1 Application to exchangeable sequences
Here, we consider a sequence of exchangeable r.v.’s such that , , , as in [8]. Taking ℋ as the σ-algebra of the permutable events, we can invoke the celebrated de Finetti’s representation theorem to show that (6) is fulfilled. Moreover, from the arguments developed in the above-mentioned paper, we obtain that the assumption on the covariances entails (7) and a.s. for all . Finally, we notice that there are many simple cases (for example, when a.s. for a suitable constant M and all ), in which (8) is easily verified. Hence, we conclude that , so that the bound (10) is in force, and an estimate of the type of (1) will follow from the application of Theorems 1-2 in Chapter 5 of [3]. To condense these facts into a unitary statement, we denote with the random probability measure which meets for all and , according to de Finetti’s theorem, and we state the following.
Proposition 3 Let be an exchangeable sequence of r.v.’s such that , , . If holds a.s. with some positive constant , then one gets
where C is an absolute constant.
The bound (13) represents an obvious generalization of (2.10) in [8] because of the arbitrariness, in the former inequality, of the weights .
1.2 Application to mixtures of Markov chains
The papers [21, 22] deal with sequences , where each takes value in a discrete state space I, whose law is a mixture of laws of Markov chains. From a Bayesian standpoint, one could think of as a Markov chain with random transition matrix, to which a prior distribution is assigned on the space of all transition matrices. The work [22] proves that, under the assumption of recurrence, this condition on the law of the sequence is equivalent to the property of partial exchangeability of the random matrix , where denotes the position of the process immediately after the n th visit to the state i. We also recall that partial exchangeability (in the sense of de Finetti) means that the distribution of V is invariant under finite permutation within rows. An equivalent condition to partial exchangeability is the existence of a σ-algebra ℋ such that the ’s are independent conditionally on it, that is,
holds for every , , and , and, in addition, each of the sequences is exchangeable. Therefore, upon assuming, for simplicity, that I is finite and that holds a.s. with a suitable function , for all and , we have that the family of r.v.’s meets conditions (6)-(8) and fits the general setting of the present paper. The ultimate motivation of this application is, in fact, to provide a Berry-Esseen inequality in order to quantify the error in approximating the law of by the standard normal distribution, where , and , , represent expectation, variance and covariance, respectively, w.r.t. the (random) stationary distribution of , given ℋ. Such a result could prove an extremely concrete achievement in Markov chain Monte Carlo settings, where the existence of a Berry-Esseen inequality allows one to estimate in order to decide whether (which is a quantity that can be simulated) is a good estimate for or not. At this stage, the well-known relation between the ’s and the ’s, contained in [22] or in Sections 9-10 of Chapter II of [23], would come in useful to establish a link between two Berry-Esseen-like inequalities: the former being relative to the family of r.v.’s , which follows from a direct application of Theorem 1, the latter being relative to the sequence . Due to the mathematical complexity of this task, this topic will be carefully developed in a forthcoming paper [24].
1.3 Application to the Boltzmann equation
In [25], the study of the rate of relaxation to equilibrium of solutions to the spatially homogeneous Boltzmann equation for Maxwellian molecules is conducted by resorting to a new probabilistic representation, set forth in Section 1.5 of that paper. The key ingredient of such a representation is the random sum , where:
-
(i)
u is a fixed point of the unitary sphere ;
-
(ii)
is a probability space with a probability measure depending on the parameter , and are suitable σ-algebras of ℱ;
-
(iii)
ν is a r.v. such that for all , and such that ν is
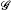 -measurable;
-measurable; -
(iv)
for any and , is a
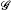 -measurable r.v., with the property that for all ;
-measurable r.v., with the property that for all ; -
(v)
for any and , is an ℋ-measurable random vector, taking values in ;
-
(vi)
is a sequence of i.i.d. random vectors taking values in , independent of ℋ and such that , for any , with , and . Here, stands for the expectation w.r.t. and is the Kronecker symbol.
After these preliminaries - whose detailed explanation the reader will find in the quoted section of [25] - it is clear that each realization of the random measure , with , has the same structure as the probability law of the sum given by (4) in the present paper. In [18, 26–28] the reader will find some analogous representations, set forth in connection with allied new forms of the Berry-Esseen inequality. Thanks to the above-mentioned link, it is important to note that Theorem 1 of the present paper, along with its proof, represents the key result needed to complete the argument developed in Section 2.2.3 of [25]. On the other hand, the application of Theorem 1 to the context of the Boltzmann equation appears as a significant use of this abstract result in its full generality, for the conditional independence is the form of stochastic dependence actually involved and the normalization to conditional variances does not necessarily occur, so that all the terms in the RHS of (9) play an active role. The successful utilization of Theorem 1 lies in the fact that the quantities , X, Y, W and Z are now easily tractable, thanks to the computations developed in Appendices A.1 and A.13 of [25].
2 Proofs
2.1 Proof of Theorem 1
Start by putting for , and recall the standard expansion for c.f.’s to write
with a suitable expression of the remainder . Superscript ˜ will be used throughout this section to remark that a certain quantity is random. Now, a plain application of the Taylor formula with the Bernstein form of the remainder gives
so that can assume one of the following forms:
Combining (8) and (15) yields a.s., for every t and . Consequently, the definition of W entails
for every t and, if ,
Now, to obtain an upper bound for in (14), observe the following facts. First, the Lyapunov inequality for moments yields and a.s. Second, implies . Hence, for every t in , one has
so that the quantity makes sense when Log is meant to be the principal branch of the logarithm. Then put
for all complex z such that (with the proviso that ) and note that the restriction of Φ to the interval is a completely monotone function. See Chapter 13 of [29]. Equation (14) now gives
and, taking account of (5),
Now, put
and exploit the conditional independence in (6) to obtain
At this stage, it remains to provide upper bounds for and , to be used throughout this section. From the definition of , one has
which implies that
for every t in , thanks to (18)-(19) and the Lyapunov inequality for moments. The monotonicity of Φ yields
for every t, and
for every t in .
Then the validity of (9) with can be derived from a combination of the above arguments starting from
First, apply the Markov inequality to conclude that
Second, after noting that
combine the elementary inequality with (25)-(26) to obtain
for every t in , with . As far as the fourth summand in the RHS of (27) is concerned, write
and proceed by analyzing each summand in the last bound separately. As to the first term, invoke (29) and use the elementary inequality to obtain
Since the Lyapunov inequality for moments entails
one gets
To continue, put for r in and note that the Lagrange form of the remainder in the Taylor formula gives
for every x in ℝ. Moreover, the Lyapunov inequality for moments shows that
Concerning the second summand in the last member of (31), take account of (34) with to write
and, by means of (35) and the definitions of T, X and Z, conclude that
For the third summand, the combination of inequality with (34) with yields
which, by means of the inequalities , (29) and (32), becomes
Finally, the elementary inequality entails
After using again the Lyapunov inequality to write
note that (32) and (38) lead to
The combination of (28), (31), (33), (36), (37) and (39) gives
At this stage, the upper bound (9) with follows from (27), (28), (30) and (40) by putting
To prove (9) when , differentiate (23) with respect to t to obtain
As the first step, write
and then proceed to study each summand in a separate way. All of these terms, except the last one, can be bounded by using inequalities already proved. First of all, the first summand coincides with the first term of (9) with , and for the second summand it suffices to recall (28). The bound for the third summand is given by (40) while, for the fourth one, use (30). Next, thanks to (35) and (38), write
As for the sixth summand, start from
Then recall (29), (35) and (38) and combine the elementary inequality with (25) and (26) to conclude that
As for the latter term in the RHS of (44), note that
Now, combining the elementary inequality with (29) and (34) entails
for every t in ℝ and hence
holds, along with
The study of the last summand in (42) reduces to the analysis of the first derivative of , which is equal to
Now, recall (16) and note that a dominated convergence argument yields
from which
for every t. Then, if t is in , then (49) gives
From the equality and the fact that when it follows that
for every t in . This, combined with (49)-(50), yields
Moreover, for every t is in , one has
The complete monotonicity of Φ entails
for every t is in and, in view of (24) and (51),
The combination of this last inequality with (49) yields
Taking account of (26), (29) and (53), the last member in (42) can be bounded as follows:
At this point, use (42) along with (28), (30), (40), (43), (45)-(47) and (54), to obtain (9) in the case , with the following functions:
To complete the proof of the proposition, it remains to study the second derivative. Therefore, differentiate (41) with respect to t to obtain
The first step consists in splitting the expectation on T and , which produces
where the terms will be defined and studied separately. First,
and a bound for this quantity is provided by multiplying by the sum of the RHSs in (30) and (40). Second,
and, according to the same line of reasoning used to get (45),
Next, as far as the second summand in the RHS of (57) is concerned, the same argument used to obtain (46)-(47) leads to
For the third summand in the RHS of (57), it is enough to exploit the definitions of X, Y, Z and W, along with (35) and (38), to have
Then can be bounded by resorting to (26) and (29). Whence,
and, from (32) and the definition of Z, one gets
The next term is , whose upper bound is given immediately by resorting to (26), (29) and (53). Therefore, since ,
To analyze , it is necessary to study the second derivative of , that is,
To bound this quantity, first recall (17) and exchange derivatives with integrals to obtain
which, after applications of the elementary inequality , gives
Whence,
is valid for every t, and
holds for each t in . From and the fact that for each t in , one deduces . This inequality, combined with (59)-(61), yields
and, for t in ,
At this stage, invoke (58) and the complete monotonicity of Φ, and combine the inequality with (20), (24), (51)-(52) and (62)-(63) to get
Therefore, an upper bound for is given by multiplying the above RHS by . Finally, the last term
can be handled without further effort by resorting to (26), (29), (35), (38) and (53). Therefore, an upper bound is obtained immediately by multiplying the RHS of (53) by .
A combination of all the last inequalities starting with (56) leads to the proof of (9) for , with the coefficients specified as follows:
2.2 Proof of Corollary 2
After an application of (11), one splits the integrals on the RHS into inner integrals (i.e., on the domain ) and outer integrals (i.e., on the domain ). Apropos of the integrals of the latter type, the Minkowski inequality entails
for every and . By using the elementary properties of the Gaussian c.f., as in the proof of Lemma 10.IV in [3], one gets
for . Moreover, after considering the conditional expectation w.r.t. ℋ, one immediately has
for every and , which concludes the study of the outer integrals by means of (12). At this stage, Theorem 1 can be invoked to bound the inner integrals, after noting that , , , are all square-integrable functions on ℝ. Apropos of the r.v.’s X, Y, Z and W, one can start by noting that the bounds , are in force directly from the definition of these random quantities. Then further computations lead immediately to and . Finally, definition (12) and show that
is uniformly bounded w.r.t. . Therefore, the inner integral of the first term in (9) can be estimated, thanks to (28), by with some suitable constant independent of n. Invoking again the relation , one arrives at the desired conclusion.
References
Berry AC: The accuracy of the Gaussian approximation to the sum of independent variates. Trans. Am. Math. Soc. 1941, 49: 122–136. 10.1090/S0002-9947-1941-0003498-3
Esseen G: Fourier analysis of distribution functions. A mathematical study of the Laplace-Gauss law. Acta Math. 1945, 77: 1–125. 10.1007/BF02392223
Petrov VV: Sums of Independent Random Variables. Springer, New York; 1975.
Chen LHY, Shao QM: A non-uniform Berry-Esseen bound via Stein’s method. Probab. Theory Relat. Fields 2001, 120: 236–254. 10.1007/PL00008782
Senatov VV: On the real accuracy of approximations in the central limit theorem. Sib. Math. J. 2011, 52: 727–746. 10.1134/S003744661104015X
Sunklodas J: Some estimates of the normal approximation for independent non-identically distributed random variables. Lith. Math. J. 2011, 51: 66–74. 10.1007/s10986-011-9108-6
Mourrat JC: On the rate of convergence in the martingale central limit theorem. Bernoulli 2013, 49: 122–136.
Blum JR, Chernoff H, Rosenblatt M, Teicher H: Central limit theorems for interchangeable processes. Can. J. Math. 1958, 10: 222–229. 10.4153/CJM-1958-026-0
Kontoyiannis I, Meyn SP: Spectral theory and limit theorems for geometrically ergodic Markov processes. Ann. Appl. Probab. 2003, 13: 304–362.
Zolotarev VM: Modern Theory of Summation of Random Variables. VSP International Science Publishers, Utrecht; 1997.
Ibragimov IA, Linnik YV: Independent and Stationary Sequences of Random Variables. Wolters-Noordhorf, Gröningen; 1971.
Barbour AD, Chen LHY: An Introduction to Stein’s Method. Singapore University Press, Singapore; 2005.
Artstein S, Ball K, Barthe F, Naor A: On the rate of convergence in the entropic central limit theorem. Probab. Theory Relat. Fields 2004, 129: 381–390. 10.1007/s00440-003-0329-4
Barron AR, Johnson O: Fisher information inequalities and the central limit theorem. Probab. Theory Relat. Fields 2004, 129: 391–409. 10.1007/s00440-004-0344-0
Bobkov, SG, Chistyakov, GP, Götze, F: Rate of convergence and Edgeworth-type expansion in the entropic central limit theorem (2011). arXiv:1104.3994. e-printatarXiv.org
Carlen EA, Soffer E: Entropy production by block variable summation and central limit theorems. Commun. Math. Phys. 1991, 140: 339–371. 10.1007/BF02099503
Goudon T, Junca S, Toscani G: Fourier-based distances and Berry-Esseen like inequalities for smooth densities. Monatshefte Math. 2002, 135: 115–136. 10.1007/s006050200010
Dolera E, Gabetta E, Regazzini E: Reaching the best possible rate of convergence to equilibrium for solutions of Kac’s equation via central limit theorem. Ann. Appl. Probab. 2009, 19: 186–201. 10.1214/08-AAP538
Wahba G: Spline Models for Observational Data. SIAM, Philadelphia; 1990.
Diaconis P: Bayesian numerical analysis. 1. In Statistical Decision Theory and Related Topics. Springer, New York; 1988:163–175.
Diaconis P, Freedman D: De Finetti’s theorem for Markov chains. Ann. Probab. 1980, 8: 115–130. 10.1214/aop/1176994828
Fortini S, Ladelli L, Petris G, Regazzini E: On mixtures of distributions of Markov chains. Stoch. Process. Appl. 2002, 100: 147–165. 10.1016/S0304-4149(02)00093-5
Bhattacharya RN, Waymire EC: Stochastic Processes with Applications. SIAM, Philadelphia; 2009.
Dolera, E: New Berry-Esseen-type inequalities for Markov chains (work in preparation)
Dolera, E, Regazzini, E: Proof of a McKean conjecture on the rate of convergence of Boltzmann-equation solutions (2012, submitted). arXiv:1206.5147. e-printatarXiv.org
Dolera E, Regazzini E: The role of the central limit theorem in discovering sharp rates of convergence to equilibrium for the solution of the Kac equation. Ann. Appl. Probab. 2010, 20: 430–461. 10.1214/09-AAP623
Gabetta E, Regazzini E: Central limit theorems for solutions of the Kac equation: speed of approach to equilibrium in weak metrics. Probab. Theory Relat. Fields 2010, 146: 451–480. 10.1007/s00440-008-0196-0
McKean HP Jr.: Speed of approach to equilibrium for Kac’s caricature of a Maxwellian gas. Arch. Ration. Mech. Anal. 1966, 21: 343–367. 10.1007/BF00264463
Feller W II. In An Introduction to Probability Theory and Its Applications. 2nd edition. Wiley, New York; 1971.
Acknowledgements
The author would like to thank professor Eugenio Regazzini, for his constructive and helpful advice, and an anonymous referee, for comments and suggestions that greatly improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that he has no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dolera, E. Estimates of the approximation of weighted sums of conditionally independent random variables by the normal law. J Inequal Appl 2013, 320 (2013). https://doi.org/10.1186/1029-242X-2013-320
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-320
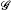 -measurable;
-measurable;