Maurey-Rosenthal domination for abstract Banach lattices

Abstract

We extend the Maurey-Rosenthal theorem on integral domination and factorization of p-concave operators from a p-convex Banach function space through $L^p$-spaces for the case of operators on abstract p-convex Banach lattices satisfying some essential lattice requirements - mainly order density of its order continuous part - that are shown to be necessary. We prove that these geometric properties can be characterized by means of an integral inequality giving a domination of the pointwise evaluation of the operator for a suitable weight also in the case of abstract Banach lattices. We obtain in this way what in a sense can be considered the most general factorization theorem of operators through $L^p$-spaces. In order to do this, we prove a new representation theorem for abstract p-convex Banach lattices with the Fatou property as spaces of p-integrable functions with respect to a vector measure.

MSC:46G10, 46E30, 46B42.

1 Introduction

The so called Maurey-Rosenthal theorem on domination and factorization of operators through $L^p$-spaces provides a large set of tools for the analysis of operators on Banach spaces. Essentially, this result provides, for a Banach lattice F of a particular class, an equivalence between the p-concavity of a Banach space valued operator $T:F\to E$ and the fact that it satisfies a pointwise integral inequality involving the norms of the evaluations $\parallel T(x)\parallel$, $x\in F$. In recent years, this (family of) theorem(s) has been studied widely by several authors, and nowadays we have a clear methodology for giving a unified version of this technique. Following the seminal ideas in [1] that allowed the understanding by means of the basic principle of a lot of similar arguments found in the mathematical literature since the sixties, several generalizations and applications have been done (see, for instance, [2–5]).

The version of this theorem that is normally used depends strongly on two facts that are deeply connected with the essential nature of the Banach function spaces.

• (1) The (topological) dual $X{(\mu )}^{\ast }$ of an order continuous Banach function space $X(\mu )$ (when defined over a σ-additive measure μ) is again a Banach function space (the Köthe dual or associate space $X{(\mu )}^{\prime }$), i.e., $X{(\mu )}^{\ast }=X{(\mu )}^{\prime }$. The second space is defined as integrals of some class of functions.

• (2) If $X(\mu )$ is a p-convex Banach function space, its p th power is again a Banach function space.

In this paper we show a general version of the Maurey-Rosenthal theorem that is obtained by relaxing these requirements as much as possible. In order to do this, we provide a function space representation of a class of Banach lattices satisfying the necessary requirements, which allows to perform the tandem ‘Banach lattices/order notions’ versus ‘function spaces/vector measures’ to provide the support for the factorization through an $L^p$-space. Therefore, the key of the arguments that prove this type of factorization is in fact the structure of the space from which the operator is defined. This is the reason why our main tool is given by the representation of Banach lattices by means of spaces $L^p(m)$ and $L_w^p(m)$ of p-integrable functions with respect to a vector measure on a δ-ring. This allows, for instance, to prove factorization theorems through ${\ell }^p(\mathrm{\Gamma })$-spaces of an uncountable set Γ.

From the point of view of the general representation of Banach lattices as function spaces, the main goal of this paper is to get a representation theorem for p-convex Banach lattices with the (σ-)Fatou property as general as possible by using vector measures defined on a δ-ring to complete the picture when the existence of a weak unit is not assumed. Section 3 is devoted to this. This becomes the main tool for proving, in Section 4, our general Maurey-Rosenthal theorem, closing in this way the question of how far this kind of arguments can be extended: examples and counterexamples are also given.

2 Preliminaries

As the reader will notice soon, the setting that is needed for proving the main result of this paper (Theorem 4) and allows to prove the most general version of the Maurey-Rosenthal theorem (Corollary 6) is unusually technical and contains some notions and arguments that are not standard in the framework of the Banach lattices. This is the reason why we include a long section of preliminaries collecting all the results that are needed.

2.1 Banach lattices

We mainly use the terminology and the notation of [6] and [7]. Let F be a real Banach lattice. An ideal $\tilde{F}$ of F is a closed subspace of F satisfying that if $y\in F$ with $|y|\le |x|$ for some $x\in \tilde{F}$, then $y\in \tilde{F}$. An ideal $\tilde{F}$ in F is said to be order dense in F if, for every $0\le x\in F$, there exists an upwards directed system $(x_{\tau })\subset \tilde{F}$ such that $0\le x_{\tau }\uparrow x$, and is said to be super order dense if this condition holds for increasing sequences. We say that F is order continuous if, for every $(x_{\tau })\subset F$ with $x_{\tau }\downarrow 0$, it follows that $\parallel x_{\tau }\parallel \downarrow 0$ and F is σ-order continuous if this is the behavior on sequences. We denote by $F_{an}$ the order continuous part of F, that is, the largest order continuous ideal in F. Similarly, the σ-order continuous part of F is the largest σ-order continuous ideal in F and is denoted by $F_a$. Of course $F_{an}\subset F_a$. We say that F has the Fatou property if, for every upwards directed system $0\le x_{\tau }\uparrow$ in F such that $sup\parallel x_{\tau }\parallel <\mathrm{\infty }$, it follows that there exists $x=sup{x}_{\tau }$ in F and, moreover, $\parallel x\parallel =sup\parallel x_{\tau }\parallel$. If this condition holds for increasing sequences, we say that F has the σ-Fatou property. Remark that under these conditions, $F_{an}=F_a$ (see, for instance, [[7], Theorems 113.1, 103.6]).

Let $1\le p<\mathrm{\infty }$. We say that F is p-convex if there exists a constant $M>0$ such that

$$\parallel {(\sum _{j=1}^n|x_j{|}^p)}^{\frac{1}{p}}\parallel \le M{\left(\sum _{j=1}^n{\parallel x_j\parallel }^p\right)}^{\frac{1}{p}}$$

for all n and $x_1,\dots ,x_n\in F$. The smallest constant satisfying the previous inequality is called the p-convexity constant of F and is denoted by ${\mathbf{M}}^{(p)}(F)$. Similarly, a linear operator $T:F\to E$, where F is a Banach lattice and E is an arbitrary Banach space, is said to be p-concave if there exists a constant $M<\mathrm{\infty }$ such that

$${\left(\sum _{j=1}^n{\parallel T(x_j)\parallel }^p\right)}^{\frac{1}{p}}\le M\parallel {(\sum _{j=1}^n|x_j{|}^p)}^{\frac{1}{p}}\parallel$$

for every choice of vectors ${(x_j)}_{j=1}^n$, $n\in \mathbb{N}$ in F. The smallest possible value of M is denoted by ${\mathbf{M}}_{(p)}(T)$.

Let F, $\tilde{F}$ be Banach lattices and let $T:F\to \tilde{F}$ be a linear operator. If $Tx\ge 0$ whenever $0\le x\in F$, the operator T is said to be positive. Every positive linear operator between Banach lattices is always continuous (see [[8], p.2] or [[9], Theorem 4.3]) and, in particular, every inclusion $F\subset \tilde{F}$ of Banach lattices with the same order is continuous. We say that T is an order isomorphism if it is one-to-one, onto and satisfies $T(x\wedge y)=Tx\wedge Ty$ for all $x,y\in F$. If, moreover, ${\parallel Tx\parallel }_{\tilde{F}}={\parallel x\parallel }_F$ for all $x\in F$, we will say that T is an order isometry. We say that F and $\tilde{F}$ are order isomorphic (order isometrics) if there is an order isomorphism (isometry) $T:F\to \tilde{F}$.

Let $(\mathrm{\Omega },\mathrm{\Sigma },\mu )$ be a measure space (without assumptions of finiteness on μ). As usual, a property holds μ-almost everywhere (briefly, μ-a.e.) if it holds except on a μ-null set. We denote by $L^0(\mu )$ the space of all measurable real functions on Ω, where functions which are equal μ-a.e. are identified. The space $L^0(\mu )$ is an Archimedean vector lattice when endowed with the μ-a.e. pointwise order. By a Banach function space (briefly, B.f.s.) related to μ, we mean a Banach space $E\subset L^0(\mu )$ satisfying that for every $f\in L^0(\mu )$, we have $f\in E$ whenever $|f|\le |g|$ with $g\in E$ and, moreover, ${\parallel f\parallel }_E\le {\parallel g\parallel }_E$. Every B.f.s. is a Banach lattice with the μ-a.e. pointwise order, in which convergence in norm of a sequence implies μ-a.e. convergence for some subsequence.

2.2 Integration with respect to vector measures on δ-rings

The spaces $L^1(\nu )$ and $L_w^1(\nu )$ of integrable and weakly integrable functions with respect to a vector measure defined on a σ-algebra and with values in a Banach space E have been studied in depth by many authors and their behavior is now well understood (see [10], [[11], Chapter 3] and the references therein). However, this setting is not rich enough for our analysis, since vector measures on σ-algebras can only be used for representing Banach lattices which have a weak unit, and our needs require to work in a more general context. In [12], there is an analysis of the space $L^1(\nu )$ with ν defined on a δ-ring and a detailed study of the lattice behavior of the corresponding space $L_w^1(\nu )$ can be found in [13]. The results in both papers give evidence of how large the difference can be between the δ-ring and σ-algebra cases and justify the use of the general framework of δ-rings in this paper. More information on the integration of vector measures on δ-rings and its applications can be found in [14–17] and [[18], pp.22-23].

For the p-convexification of these spaces - the spaces $L^p(\nu )$ and $L_w^p(\nu )$ of p-integrable functions - the fundamental results that are needed in this paper are also known. When the vector measure ν is defined on a σ-algebra, all the relevant (geometric, lattice, topological) properties of the spaces $L^p(\nu )$ of p-integrable functions and $L_w^p(\nu )$ of weakly p-integrable functions with $1\le p<\mathrm{\infty }$ can be found in [19] and [11, 19, 20]. For the δ-ring case, the study of the main lattice properties of the spaces $L^p(\nu )$ and $L_w^p(\nu )$ is developed in [21], where the general case $0<p<\mathrm{\infty }$ is also considered (although for $0<p<1$ these spaces are not necessarily Banach spaces, completeness is proved, but under a quasinorm, and the analogous definitions for Banach lattices are considered).

The theory of integration with respect to a vector measure defined on a δ-ring is due to Lewis [22] and Masani and Niemi [23, 24] (see also [12, 13] and [21]). This integration theory extends the classical one for vector measures defined on σ-algebras. Let ℛ be a δ-ring of subsets of an abstract set Ω, that is, a ring closed under countable intersections. We denote by ${\mathcal{R}}^{\mathrm{loc}}$ the σ-algebra given by the subsets $A\subset \mathrm{\Omega }$ such that $A\cap B\in \mathcal{R}$ for all $B\in \mathcal{R}$. Clearly, if ℛ is a σ-algebra, then ${\mathcal{R}}^{\mathrm{loc}}=\mathcal{R}$. We write $\mathcal{M}({\mathcal{R}}^{\mathrm{loc}})$ for the space of measurable real functions on $(\mathrm{\Omega },{\mathcal{R}}^{\mathrm{loc}})$ and $\mathcal{S}(\mathcal{R})$ for the space of simple functions with support in ℛ (or ℛ-simple functions).

Let $\lambda :\mathcal{R}\to \mathbb{R}$ be a countably additive measure, that is, for every sequence $(A_n)$ of pairwise disjoint sets in ℛ with $\bigcup A_n$ in ℛ, the sum $\sum \lambda (A_n)$ converges to $\lambda (\bigcup A_n)$. The variation of λ is the countably additive measure $|\lambda |:{\mathcal{R}}^{\mathrm{loc}}\to [0,\mathrm{\infty }]$ defined by

$$|\lambda |(A)=sup\{\sum |\lambda (A_i)|:(A_i)\text{ finite disjoint sequence in }\mathcal{R}\cap 2^A\}.$$

We have that $|\lambda |(A)<\mathrm{\infty }$ for every $A\in \mathcal{R}$. The space $L^1(\lambda )$ of integrable functions with respect to λ is defined as the space $L^1(|\lambda |)$ with the usual norm. Every ℛ-simple function $\phi ={\sum }_{i=1}^n{\alpha }_i{\chi }_{A_i}$ is in $L^1(\lambda )$, where the integral of φ with respect to λ is defined by $\int \phi d\lambda ={\sum }_{i=1}^n{\alpha }_i\lambda (A_i)$. Furthermore, the space $\mathcal{S}(\mathcal{R})$ is dense in $L^1(\lambda )$. For every $f\in L^1(\lambda )$, the integral of f with respect to λ is defined, as usual, as $\int fd\lambda =lim\int {\phi }_{n}d\lambda$ for any sequence $({\phi }_n)\subset \mathcal{S}(\mathcal{R})$ converging to f in $L^1(\lambda )$.

Let E be a Banach space and let $\nu :\mathcal{R}\to E$ be a vector measure, that is, for every sequence $(A_n)$ of pairwise disjoint sets in ℛ with $\bigcup A_n\in \mathcal{R}$, the sum $\sum \nu (A_n)$ converges to $\nu (\bigcup A_n)$ in E. The semivariation of ν is the map $\parallel \nu \parallel :{\mathcal{R}}^{\mathrm{loc}}\to [0,\mathrm{\infty }]$ given by $\parallel \nu \parallel (A)=sup\{|x^{\ast }\nu |(A):x^{\ast }\in B_{E^{\ast }}\}$ for all $A\in {\mathcal{R}}^{\mathrm{loc}}$, where $|x^{\ast }\nu |$ is the variation of the measure $x^{\ast }\nu :\mathcal{R}\to \mathbb{R}$ given by $x^{\ast }\nu (A)=〈\nu (A),x^{\ast }〉$, $E^{\ast }$ denotes the topological dual of E and $B_{E^{\ast }}$ the unit ball of $E^{\ast }$. The semivariation of ν is monotone increasing, countably subadditive, finite on ℛ and satisfies $\frac{1}{2}\parallel \nu \parallel (A)\le sup\{{\parallel \nu (B)\parallel }_X:B\in \mathcal{R}\cap 2^A\}\le \parallel \nu \parallel (A)$ for all $A\in {\mathcal{R}}^{\mathrm{loc}}$. Thus, the vector measure ν is bounded (i.e., its range is a bounded set in E) if and only if $\parallel \nu \parallel (\mathrm{\Omega })<\mathrm{\infty }$. A set $A\in {\mathcal{R}}^{\mathrm{loc}}$ is ν-null if $\parallel \nu \parallel (A)=0$, or equivalently, $\nu (B)=0$ for all $B\in \mathcal{R}\cap 2^A$ and a property holds ν-almost everywhere (briefly, ν-a.e.) if it holds as usual except on a ν-null set.

A function $f\in \mathcal{M}({\mathcal{R}}^{\mathrm{loc}})$ is said to be weakly integrable with respect to ν if $f\in L^1(x^{\ast }\nu )$ for all $x^{\ast }\in E^{\ast }$, or equivalently, if ${\parallel f\parallel }_{\nu }<\mathrm{\infty }$, where

$${\parallel f\parallel }_{\nu }=\underset{x^{\ast }\in B_{E^{\ast }}}{sup}\int |f|d\left|x^{\ast }\nu \right|.$$

We denote by $L_w^1(\nu )$ the space of all weakly integrable functions with respect to ν, where functions which are equal ν-a.e. are identified, which is a Banach space when endowed with the norm ${\parallel \cdot \parallel }_{\nu }$. A function $f\in L_w^1(\nu )$ is integrable with respect to ν if, for each $A\in {\mathcal{R}}^{\mathrm{loc}}$, there exists a vector denoted by ${\int }_{A}fd\nu \in E$, satisfying the barycentric formula $x^{\ast }({\int }_{A}fd\nu )={\int }_{A}fd{x}^{\ast }\nu$ for all $x^{\ast }\in E^{\ast }$. We write $\int fd\nu$ for ${\int }_{\mathrm{\Omega }}fd\nu$. We denote by $L^1(\nu )$ the space of all integrable functions with respect to ν. Then, since $L^1(\nu )$ is a closed subspace of $L_w^1(\nu )$, it is a Banach space with the norm ${\parallel \cdot \parallel }_{\nu }$. Moreover, $\mathcal{S}(\mathcal{R})$ is dense in $L^1(\nu )$, where for every ℛ-simple function $\phi ={\sum }_{i=1}^n{\alpha }_i{\chi }_{A_i}$, we have that $\int \phi d\nu ={\sum }_{i=1}^n{\alpha }_i\nu (A_i)$. The equality $L_w^1(\nu )=L^1(\nu )$ holds whenever the space E does not contain a copy of $c_0$ (see [[22], Theorem 5.1]).

We will identify $L^0(\nu )=L^0(\mu )$ and say B.f.s. related to ν for B.f.s. related to μ, for any measure $\mu :{\mathcal{R}}^{\mathrm{loc}}\to [0,\mathrm{\infty }]$ with the same null sets as ν (the existence of such a measure is guaranteed in [[25], Theorem 3.2]). Therefore, $L^1(\nu )$ and $L_w^1(\nu )$ are both B.f.s.’ related to ν. The space $L^1(\nu )$ is always order continuous and $L_w^1(\nu )$ have the σ-Fatou property. Furthermore, $L^1(\nu )$ is always order dense in $L_w^1(\nu )$ (actually, in $L^0(\nu )$) and ${(L_w^1(\nu ))}_a=L^1(\nu )$. We denote by ${[L^1(\nu )]}_{\sigma \text{-F}}$ the minimal B.f.s. related to ν, with the σ-Fatou property and containing $L^1(\nu )$. It can be described as

$${[L^1(\nu )]}_{\sigma \text{-F}}=\{f\in L_w^1(\nu ):supp(f)=(\bigcup A_n)\cup N,(A_n)\subset \mathcal{R},N\nu \text{-null}\}.$$

The integration operator $I_{\nu }:L^1(\nu )\to E$ given by $I_{\nu }(f)=\int fd\nu$ is linear and continuous with $\parallel I_{\nu }(f)\parallel \le {\parallel f\parallel }_{\nu }$. A vector measure $\nu :\mathcal{R}\to E$ with values in a Banach lattice E is positive if $\nu (A)\ge 0$ for all $A\in \mathcal{R}$.

Given $0<p<\mathrm{\infty }$, the p th power space of $L_w^1(\nu )$ is defined as $L_w^p(\nu )=\{f\in L^0(\nu ):{|f|}^p\in L_w^1(\nu )\}$ and a function in $L_w^p(\nu )$ will be called weakly p-integrable with respect to ν. Similarly, the p th power space of $L^1(\nu )$ is defined as $L^p(\nu )=\{f\in L^0(\nu ):{|f|}^p\in L^1(\nu )\}$, and a function in $L^p(\nu )$ will be called p-integrable with respect to ν. Both spaces are B.f.s.’ related to ν for $p\ge 1$ and q-B.f.s.’ for $p<1$ when the lattice (quasi)norm given by ${\parallel f\parallel }_{p,\nu }={\parallel {|f|}^p\parallel }_{\nu }^{\frac{1}{p}}$, $f\in L_w^p(\nu )$, is considered. The space $L^p(\nu )$ is order continuous and the space $L_w^p(\nu )$ has the σ-Fatou property. Moreover, $\mathcal{S}(\mathcal{R})$ is dense in $L^p(\nu )$; ${(L_w^p(\nu ))}_a=L^p(\nu )$; $L^p(\nu )$ is order dense in $L_w^p(\nu )$ (also in $L^0(\nu )$) and if $L_w^1(\nu )$ has the Fatou property, so does $L_w^p(\nu )$. Related to the convexity behavior of these spaces, both are p-convex with p-convexity constant ${\mathbf{M}}^{(p)}(L_w^p(\nu ))={\mathbf{M}}^{(p)}(L^p(\nu ))=1$.

3 Representing p-convex Banach lattices

Representation of Banach lattices as spaces of integrable functions with respect to a vector measure is nowadays a well-known useful technique. Depending on the fact that either the lattice contains a weak unit or not, either vector measures on σ-algebras or on δ-rings must be used. Curbera proved in [[26], Theorem 8] that an order continuous Banach lattice F with a weak unit is always order isometric to a space $L^1(\nu )$, where ν is defined on a σ-algebra. If the existence of a weak unit is not assumed, the result remains true but for ν defined on a δ-ring. This was first stated in [[18], pp.22-23] with an outlined proof and later in [[27], Theorem 5] with a full detailed proof. Thinking now about the space $L_w^1(\nu )$, Curbera and Ricker showed in [[28], Theorem 2.5] that every Banach lattice F with the σ-Fatou property, having a weak unit which belongs to the σ-order continuous part $F_a$ of F, is order isometric to a space $L_w^1(\nu )$ with ν defined on a σ-algebra. Again, the corresponding result in the case when F has not a weak unit can be established by using a vector measure defined on a δ-ring as Delgado and Juan proved in [[27], Theorem 10]. In this case, every Banach lattice F with the Fatou property, and such that its σ-order continuous part is an order dense subset in F, can be represented as a space $L_w^1(\nu )$ for some vector measure ν defined on a δ-ring. Furthermore, a representation theorem for the class of σ-Fatou Banach lattices F with the σ-order continuous part as a super order dense ideal in F, using again vector measures on δ-rings, is established in [[13], Proposition 6.1]. In this case, F is order isometric to the σ-Fatou completion of $L^1(\nu )$.

Similar results are known for representing Banach lattices with convexity properties, and in this case, the spaces of p-integrable functions with respect to vector measures play a fundamental role. For $1<p<\mathrm{\infty }$, if F is an order continuous p-convex Banach lattice, then F is order isomorphic to an $L^p$-space with ν defined on a δ-ring [[21], Theorem 10]. When there exists also a weak unit in F, the Banach lattice can be represented with an $L^p$-space but with ν defined on a σ-algebra (see [[20], Proposition 2.4]). On the other hand, if E is a p-convex Banach lattice with the σ-Fatou property and has a weak unit belonging to $E_a$, then E is order isomorphic to a space $L_w^p(\nu )$ with ν on a σ-algebra [29]. The aim of this section is to get a representation theorem for p-convex Banach lattices with the (σ-)Fatou property as general as possible by using vector measures defined on a δ-ring to complete the picture when the existence of a weak unit is not assumed. The starting point to prove this result is the corresponding representation theorem for the case $p=1$. In the proof of this theorem, the vector measure which allows to establish the order isometry has a special behavior (the so-called ℛ-decomposability), under which the space $L_w^1(\nu )$ has the Fatou property (see [[27], Proposition 8] and [[13], Theorem 5.8 and Section 6]). We recall here the corresponding definition as follows.

A vector measure ν is said to be ℛ-decomposable if we can write $\mathrm{\Omega }=({\bigcup }_{\alpha \in \mathrm{\Delta }}{\mathrm{\Omega }}_{\alpha })\cup N$, where $N\in {\mathcal{R}}^{\mathrm{loc}}$ is a ν-null set and $\{{\mathrm{\Omega }}_{\alpha }:\alpha \in \mathrm{\Delta }\}$ is a family of pairwise disjoint sets in ℛ satisfying that

• (i) if $A_{\alpha }\in \mathcal{R}\cap 2^{{\mathrm{\Omega }}_{\alpha }}$ for all $\alpha \in \mathrm{\Delta }$, then ${\bigcup }_{\alpha \in \mathrm{\Delta }}{A}_{\alpha }\in {\mathcal{R}}^{\mathrm{loc}}$, and

• (ii) for each $x^{\ast }\in X^{\ast }$, if $Z_{\alpha }\in \mathcal{R}\cap 2^{{\mathrm{\Omega }}_{\alpha }}$ is $|x^{\ast }\nu |$-null for all $\alpha \in \mathrm{\Delta }$, then ${\bigcup }_{\alpha \in \mathrm{\Delta }}{Z}_{\alpha }$ is $|x^{\ast }\nu |$-null.

(N can be taken to be disjoint with ${\bigcup }_{\alpha \in \mathrm{\Delta }}{\mathrm{\Omega }}_{\alpha }$).

Note that each p-convex Banach lattice F can be renormed equivalently in a way that F with the new norm and the same order is a p-convex Banach lattice with p-convexity constant equal to 1 (see [[8], Proposition 1.d.8]).

Theorem 1 Let $p>1$ and let F be a p-convex Banach lattice with p-convexity constant equal to 1, having the Fatou property and such that its σ-order continuous part $F_a$ is an order dense subset. Then there exists a vector measure ν on a δ-ring and with values in $F_a$ such that F and $L_w^p(\nu )$ are order isometric.

Proof The hypothesis on F gives an ℛ-decomposable vector measure ${\nu }_1$ on a δ-ring ℛ and an order isometry $\phi :F\to L_w^1({\nu }_1)$ (see Theorem 10 in [27] and Section 6 in [13]). Remark that $L_w^1({\nu }_1)$ is then p-convex with p-convexity constant equal to 1 and, consequently, the space $L_w^{1/p}({\nu }_1)$ is a B.f.s., that is, its quasi-norm is actually a norm (see [[13], Proposition 6]). Moreover, $L_w^{1/p}({\nu }_1)$ has the Fatou property and $L^{1/p}({\nu }_1)$ is order dense in $L_w^{1/p}({\nu }_1)$ (see the comments before Section 4 in [21]). Take now the vector measure ${\nu }_2:\mathcal{R}\to L^{1/p}({\nu }_1)$ defined by ${\nu }_2(A)={\chi }_A$, $A\in \mathcal{R}$ for which the integration operator $I_{{\nu }_2}:L^1({\nu }_2)\to L^{1/p}({\nu }_1)$ is the identity map and $L^1({\nu }_2)=L^{1/p}({\nu }_1)$ with equal norms (see the proof of Theorem 10 in [21]). It can be checked easily that ${\nu }_2$ is also ℛ-decomposable since ${\nu }_1$ is; in order to see this, note that the vector measures ${\nu }_1$ and ${\nu }_2$ have the same null sets, and follow the construction of ℛ in Section 3 in [27]. Hence, $L_w^1({\nu }_2)$ has the Fatou property (see [[13], Theorem 5.8]).

We claim now that $L_w^1({\nu }_2)=L_w^{1/p}({\nu }_1)$ with equal norms. For showing this, take $0\le f\in L_w^1({\nu }_2)$. Since $L^1({\nu }_2)$ is order dense in $L^0({\nu }_2)$ (see Remark 4.3 in [13]), there exists an upwards directed system ${(f_{\tau })}_{\tau }$ in $L^1({\nu }_2)$ such that $0\le f_{\tau }\uparrow f$ in $L^0({\nu }_2)$. Then $0\le f_{\tau }\uparrow$ in $L_w^{1/p}({\nu }_1)$ and $sup{\parallel f_{\tau }\parallel }_{\frac{1}{p},{\nu }_1}=sup{\parallel f_{\tau }\parallel }_{{\nu }_2}\le {\parallel f\parallel }_{{\nu }_2}$. Therefore, the Fatou property of $L_w^{1/p}({\nu }_1)$ gives $h\in L_w^{1/p}({\nu }_1)$ such that ${\parallel h\parallel }_{\frac{1}{p},{\nu }_1}={sup}_{\tau }{\parallel f_{\tau }\parallel }_{\frac{1}{p},{\nu }_1}$. Since for each τ we have that $f_{\tau }\le h$ ${\nu }_1$-a.e. or, equivalently, ${\nu }_2$-a.e., then $f\le h$ and so $f\in L_w^{1/p}({\nu }_1)$. On the other hand, $f_{\tau }\le f$ ${\nu }_2$-a.e. (i.e., ${\nu }_1$-a.e.) for all τ and thus $h\le f$. Therefore, ${\parallel f\parallel }_{\frac{1}{p},{\nu }_1}={\parallel h\parallel }_{\frac{1}{p},{\nu }_1}={sup}_{\tau }{\parallel f_{\tau }\parallel }_{\frac{1}{p},{\nu }_1}={sup}_{\tau }{\parallel f_{\tau }\parallel }_{{\nu }_2}$ due to the Fatou property of $L_w^1({\nu }_2)$ as $0\le f_{\tau }\uparrow f$ also in $L_w^1({\nu }_2)$. By taking positive and negative parts for a general $f\in L_w^1({\nu }_2)$, we have that $L_w^1({\nu }_2)\subset L_w^{1/p}({\nu }_1)$ with equal norms.

The converse inclusion can be proved by using the same arguments. Therefore, the equality $L_w^1({\nu }_2)=L_w^{1/p}({\nu }_1)$ holds with equal norms. Consequently, $L_w^p({\nu }_2)=L_w^1({\nu }_1)$ with equal norms, and hence E and $L_w^p({\nu }_2)$ are order isometric. □

Remark 2 A proof based on similar arguments to those in the previous theorem allows us to represent p-convex Banach lattices (with p-convexity constant equal to 1) having the σ-Fatou property and such that $E_a$ is super order dense in E. In this case, E is order isometric to ${[L^p(\nu )]}_{\sigma \text{-F}}$ for some vector measure ν defined on a δ-ring. This result generalizes [[29], Theorem 4] where E has a weak unit in $E_a$. Remark that our proof differs from the one given in [[29], Theorem 4].

4 The Maurey-Rosenthal theorem for abstract Banach lattices

In this section we prove the main result of this paper. As we said in the introduction, our aim is to explore the limits of the arguments that allow to prove the factorization theorem regarding the structure of the Banach lattice where the operator is defined.

We say that an operator $T:G\to E$ from a closed subspace G of a Banach lattice F with $F_{an}\subset G\subset F$ on a Banach space E is Fatou if it satisfies that for every upwards directed system $0\le x_{\tau }\uparrow x$, with $x_{\tau }\in F_{an}$ for every τ and $x\in G$, we have that ${lim}_{\tau }\parallel T(x_{\tau })\parallel =\parallel T(x)\parallel$. Continuous operators between two Banach lattices F and $\tilde{F}$, when restricted to $G=F_{an}$, are clearly Fatou. Also, positive order continuous operators from a Banach lattice F into a Fatou Banach lattice $\tilde{F}$, when restricted to a closed subspace G of F with $F_{an}\subset G\subset F$, are so (for the definition of order continuous operator, see, for instance, [9]). Obviously, there are examples of operators which are not Fatou, as we show in the next example.

Example 3 Consider ${\ell }^{\mathrm{\infty }}(\mathrm{\Gamma })$, where Γ is an uncountable set. Take its (σ)-order continuous part $c_0(\mathrm{\Gamma })$ and a continuous operator $S:c_0(\mathrm{\Gamma })\to {\ell }^{\mathrm{\infty }}(\mathrm{\Gamma })$ with $\parallel S\parallel =\frac{1}{2}$. Use the Hahn-Banach theorem to find a functional $\varphi \in {({\ell }^{\mathrm{\infty }}(\mathrm{\Gamma }))}^{\ast }$ such that $\varphi (x)=0$ for all $x\in c_0(\mathrm{\Gamma })$ and $\varphi ({\chi }_{\mathrm{\Gamma }})=1$, and define the operator $T:c_0(\mathrm{\Gamma })+span\{{\chi }_{\mathrm{\Gamma }}\}\to {\ell }^{\mathrm{\infty }}(\mathrm{\Gamma })$ given by $T(\cdot )=S(P_{c_0(\mathrm{\Gamma })}\cdot )+\varphi (\cdot ){\chi }_{\mathrm{\Gamma }}$, where $P_{c_0(\mathrm{\Gamma })}$ is the projection of every element of the (direct) sum $c_0(\mathrm{\Gamma })+span\{{\chi }_{\mathrm{\Gamma }}\}$ endowed with the max norm on $c_0(\mathrm{\Gamma })$. To see that T is not Fatou, just consider $x={\chi }_{\mathrm{\Gamma }}$, and for every finite set N of Γ, define $x_N$ as the characteristic function ${\chi }_N$. Take the increasing net $\{x_N:N\text{ finite},N\subset \mathrm{\Gamma }\}$ (order is given by inclusion of the indexes), and notice that for all N, $\parallel T(x_N)\parallel =\parallel S(x_N)\parallel \le \frac{1}{2}$ and $\parallel T(x)\parallel =\parallel {\chi }_{\mathrm{\Gamma }}\parallel =1$. We will come back to this example in Remark 7(2).

Theorem 4 Let $1\le p<\mathrm{\infty }$ and consider a positive vector measure $\nu :\mathcal{R}\to F$ on a δ-ring with values in a Banach lattice, and a closed subspace of measurable functions Y such that $L^p(\nu )\subset Y\subset L_w^p(\nu )$. Let $T:Y\to E$ be a Fatou operator, where E is a Banach space. Then the following statements are equivalent.

• (1) $T{|}_{L^p(\nu )}$ is p-concave.

• (2) There exists a measure $\eta :{\mathcal{R}}^{\mathrm{loc}}\to {\mathbb{R}}^{+}$ that is absolutely continuous with respect to ν and such that

  $$\parallel T(f)\parallel \le {(\int {|f|}^{p}d\eta )}^{1/p}<+\mathrm{\infty },f\in Y.$$

• (3) There are a scalar measure $\eta :{\mathcal{R}}^{\mathrm{loc}}\to {\mathbb{R}}^{+}$ and a continuous operator $S:E\to L^p(\eta )$ such that the following diagram commutes:

  

where $[i]$ is the inclusion/quotient map given by $[i](f)=[f]$ - the equivalence class of f with respect to η.

Proof Let us prove $\text{(1)}\to \text{(2)}$. Consider first the restriction $T_0$ of T to the space $L^p(\nu )$. A standard separation procedure gives the existence of a positive element ${\varphi }_0:=M_{(p)}(T){\varphi }_1$ of ${(L^1(\nu ))}^{\ast }$ (where ${\varphi }_1\in B_{L^1{(\nu )}^{\ast }}$) satisfying that

$$\parallel T_0(f)\parallel \le {〈{|f|}^p,{\varphi }_0〉}^{1/p},f\in L^p(\nu ).$$

To see this, since ${(L^p(\nu ))}^{\frac{1}{p}}=L^1(\nu )$, it is enough to apply Ky-Fan’s lemma to the concave family of convex continuous functions $\psi :(B_{L^1{(\nu )}^{\ast }},{\tau }_{w\ast })\to \mathbb{R}$ defined as

$$\psi \left(x^{\ast }\right):=\sum _{i=1}^n{\parallel T(f_i)\parallel }^p-{(M_{(p)}(T))}^p〈\sum _{i=1}^n{|f_i|}^p,x^{\ast }〉,x^{\ast }\in B_{{(L^1(\nu ))}^{\ast }},$$

for each finite set $f_1,\dots ,f_n\in L^p(\nu )$ (see, for instance, this technique in [1] - see Corollary 5 and the proof of Theorem 1 - or the proof of Theorem 4.1 in [3]).

Let us show now that we can identify ${\varphi }_0$ with a measure on the measurable space $(\mathrm{\Omega },{\mathcal{R}}^{\mathrm{loc}})$. Since the space $L^1(\nu )$ is order continuous and ν is positive, the inequalities

$${\varphi }_0({\chi }_A)\le \parallel {\varphi }_0\parallel \cdot {\parallel {\chi }_A\parallel }_{L^1(\nu )}=\parallel {\varphi }_0\parallel \cdot \parallel \nu \parallel (A)=\parallel {\varphi }_0\parallel \cdot {\parallel \nu (A)\parallel }_F,A\in \mathcal{R}$$

give easily that the set function $\eta :\mathcal{R}\to {\mathbb{R}}^{+}$ defined by $\eta (A)={\varphi }_0({\chi }_A)$ is countably additive, and so it defines a measure with the domain in the semi-ring ℛ. Using the Carathéodory extension procedure (see, for instance, Section 9.4 in [30]), we get that η can be extended to the σ-algebra of measurable sets with respect to the outer measure defined by ${\eta }^{\ast }$.

So, we only need to show the following claim: each set in ${\mathcal{R}}^{\mathrm{loc}}$ is η-measurable. To see that, we have to prove that for a set $B\in {\mathcal{R}}^{\mathrm{loc}}$, $\eta (A)={\eta }^{\ast }(A\cap B)+{\eta }^{\ast }(A\cap B^c)$ for each $A\in \mathcal{R}$ (see, for instance, Lemma 9.26 in [30]). Notice that fixed $A\in \mathcal{R}$, $A\cap B$ and $A\cap B^c$ are also in ℛ due to the definition of ${\mathcal{R}}^{\mathrm{loc}}$, so we really have to prove that ${\varphi }_0({\chi }_A)={\varphi }_0({\chi }_{A\cap B})+{\varphi }_0({\chi }_{A\cap B^c})$ for every $A\in \mathcal{R}$. Finally, since ${\chi }_A$, ${\chi }_{A\cap B}$ and ${\chi }_{A\cap B^c}$ belong to $L^1(\nu )$, the linearity of ${\varphi }_0$ proves the claim.

Remark also that η is absolutely continuous with respect to ν, that is, if $B\in {\mathcal{R}}^{\mathrm{loc}}$ is ν-null, then B is also η-null. To prove this fact, it suffices to fix $A\in \mathcal{R}$ with $A\subset B$ and check that $\eta (A)=0$, but $\eta (A)={\varphi }_0({\chi }_A)\le \parallel {\varphi }_0\parallel \cdot {\parallel {\chi }_A\parallel }_{L^1(\nu )}=\parallel {\varphi }_0\parallel \cdot \parallel \nu \parallel (A)=0$ since B is ν-null. Consequently, a (ν-a.e.) class in $L^0(\nu )$ represented by f can be considered then a (η-a.e.) class in $L^0(\eta )$ represented by the same f. We will call again η the restriction of ${\eta }^{\ast }$ to ${\mathcal{R}}^{\mathrm{loc}}$.

Each ℛ-simple function is of course η-integrable - recall that η comes from a functional of ${(L^1(\nu ))}^{\ast }$ - and then the density of this set in $L^p(\nu )$ gives that the inequality involving ${\varphi }_0$ that was proved using Ky Fan’s lemma can be rewritten as

$$\parallel T_0(f)\parallel \le {(\int {|f|}^{p}d\eta )}^{1/p},f\in L^p(\nu ),$$

since for such functions, $\int {|f|}^{p}d\eta =〈{|f|}^p,{\varphi }_0〉$. Notice also that for all $f\in L^p(\nu )$, we have that $\int {|f|}^{p}d\eta <+\mathrm{\infty }$. For this aim, take $0\le f\in L^p(\nu )$ and an increasing sequence $(f_n)$ of ℛ-simple functions such that $0\le f_n\uparrow f$ in the ν-a.e. order and in the norm of $L^p(\nu )$. Then $0\le f_n\uparrow$ in $L^p(\eta )$. Moreover, for every n,

$$\int {|f_n|}^{p}d\eta =〈{|f_n|}^p,{\varphi }_0〉\le \parallel f_n^p\parallel \cdot {\parallel {\varphi }_0\parallel }_{L^1{(\nu )}^{\ast }}\le {\parallel f^p\parallel }_{L^1(\nu )}\cdot {\parallel {\varphi }_0\parallel }_{L^1{(\nu )}^{\ast }},$$

so ${sup}_n{\parallel f_n\parallel }_{L^p(\eta )}<+\mathrm{\infty }$, and consequently $f\in L^p(\eta )$ with ${sup}_n{\parallel f_n\parallel }_{L^p(\eta )}={\parallel f\parallel }_{L^p(\eta )}$ due to the σ-Fatou property of the space $L^p(\eta )$. The same occurs for a general $f\in L^p(\eta )$ following a standard procedure with $f=f^{+}-f^{-}$. This allows to write a factorization of $T_0$ through the space $L^p(\eta )$.

Now we prove that this is enough for getting an extension of $T_0$ that coincides with T using the same construction that proves Proposition 2.7 in [31]. In the proof, the operator considered is the integration map. As this is not our case, this is the reason why we write here a detailed proof. Take an element $0\le f\in Y$. Then there is an upwards directed system $(f_{\tau })\subset L^p(\nu )$ with $0\le f_{\tau }\uparrow f$ ν-a.e. due to the order density of $L^p(\nu )$ in $L_w^p(\nu )$. Moreover, following the same arguments as above, $f_{\tau }\uparrow$ in $L^p(\eta )$ with ${sup}_{\tau }{\parallel f_{\tau }\parallel }_{L^p(\eta )}<+\mathrm{\infty }$. Finally, since the space $L^p(\eta )$ is order continuous and has the σ-Fatou property, Theorem 113.4 in [7] yields that $L^p(\eta )$ has the Fatou property, and so $f\in L^p(\eta )$. Now the Fatou property of the operator gives also that ${lim}_{\tau }\parallel T(f_{\tau })\parallel =\parallel T(f)\parallel$. Consequently, since for every τ,

$$\parallel T(f_{\tau })\parallel =\parallel T_0(f_{\tau })\parallel \le {\parallel f_{\tau }\parallel }_{L^p(\eta )},$$

we have that

$$\parallel T(f)\parallel =\underset{\tau }{lim}\parallel T_0(f_{\tau })\parallel \le \underset{\tau }{lim}{\parallel f_{\tau }\parallel }_{L^p(\eta )}=\underset{\tau }{sup}{\parallel f_{\tau }\parallel }_{L^p(\eta )}={\parallel f\parallel }_{L^p(\eta )},$$

the last equality due again to the Fatou property of $L^p(\eta )$. Therefore,

$$\parallel T(f)\parallel \le {(\int {|f|}^{p}d\eta )}^{1/p}$$

holds also for $0\le f\in Y$. Again, a standard argument - decomposing a general $f\in Y$ as $f^{+}-f^{-}$, $0\le f^{+},f^{-}$ - gives the result for all $f\in Y$.

For $\text{(2)}\to \text{(3)}$, consider the inclusion/quotient map $[i]:Y\to L^p(\eta )$, given by $[i](f):=[f]$, that is well defined by the absolute continuity of η with respect to ν. Notice that the ℛ-simple functions are dense in $L^p(\eta )$, and so the range $[i](Y)$ is obviously dense in $L^p(\eta )$, and we can define an operator $S:L^p(\eta )\to E$ by $S(f):=T(f)$ for each ℛ-simple function $f\in Y$ (note that $T(f)=T(f^{\prime })$ if $f=f^{\prime }$ η-a.e.), and then for all functions in $L^p(\eta )$ by density.

The implication $\text{(3)}\to \text{(1)}$ can be proved just by considering the following inequalities:

$$\begin{array}{rcl}{\left(\sum _{i=1}^n{\parallel T(f_i)\parallel }^p\right)}^{\frac{1}{p}}& =& {\left(\sum _{i=1}^n{\parallel S\circ [i](f_i)\parallel }^p\right)}^{\frac{1}{p}}\le \parallel S\parallel {\left(\sum _{i=1}^n{\parallel [i](f_i)\parallel }_{L^p(\eta )}^p\right)}^{\frac{1}{p}}\\ =& \parallel S\parallel \cdot {\parallel {\left(\sum _{i=1}^n{|f_i|}^p\right)}^{\frac{1}{p}}\parallel }_{L^p(\eta )}\le \parallel S\parallel \cdot {\parallel {\left(\sum _{i=1}^n{|f_i|}^p\right)}^{\frac{1}{p}}\parallel }_{L^p(\nu )},\end{array}$$

which hold for every finite family ${(f_i)}_{i=1}^n\subset Y$ and $n\in \mathbb{N}$, where we use the fact that $L^p(\eta )$ is a p-convex space with p-convexity constant equal to 1. □

Example 5 Consider $1\le p<q<\mathrm{\infty }$ and the Fatou operator $T:{\ell }^q(\mathrm{\Gamma })\to E$, where Γ is uncountable. Remark that ${\ell }^q(\mathrm{\Gamma })$ is clearly q-convex and so ${\ell }^q(\mathrm{\Gamma })$ is p-convex (see Proposition 1.d.5 in [8]). Since the space is order continuous, Theorem 10 in [21] gives the existence of a vector measure on a δ-ring $\nu :\mathcal{R}\to {\ell }^{\frac{q}{p}}(\mathrm{\Gamma })$ such that ${\ell }^q(\mathrm{\Gamma })$ is order isomorphic to $L^p(\nu )$. Furthermore, since ${\ell }^{\frac{q}{p}}(\mathrm{\Gamma })$ does not have a copy of $c_0$, $L^1(\nu )=L_w^1(\nu )$ and so $L^p(\nu )=L_w^p(\nu )$ also. Notice that then the operator T can be considered as a Fatou operator from $L_w^p(\nu )$ into E. Now, if T is p-concave, Theorem 4 assures that there is a factorization through a space $L^p(\eta )$. This natural and easy Maurey-Rosenthal type theorem, which is a direct consequence of Theorem 4, can only be proved using the abstract setting of the vector measure representation of p-convex Banach lattices that has been shown in the previous section. Remark that ${\ell }^q(\mathrm{\Gamma })$ cannot be written as an $L^p(\beta )$ for a vector measure β defined on a σ-algebra since the space has not a weak unit.

Corollary 6 Let $p\ge 1$, E be a Banach space and F be a p-convex Banach lattice with the Fatou property. Suppose that $F_a$ is order dense in F. Consider a closed subspace G such that $F_a\subset G\subset F$. Then the following statements are equivalent for a Fatou operator $T:G\to E$.

• (1) $T{|}_{F_a}$ is p-concave.

• (2) There exist a vector measure ν on a δ-ring $\mathcal{R}\to F_a$, a scalar measure $\eta :{\mathcal{R}}^{\mathrm{loc}}\to {\mathbb{R}}^{+}$ that is absolutely continuous with respect to ν and an order isomorphism on the range $\phi :F\to L_w^p(\nu )$ such that

  $$\parallel T(x)\parallel \le {(\int {|\phi (x)|}^{p}d\eta )}^{1/p}<+\mathrm{\infty },x\in G.$$

• (3) There are a vector measure on a δ-ring $\nu :\mathcal{R}\to F_a$, a scalar measure $\eta :{\mathcal{R}}^{\mathrm{loc}}\to {\mathbb{R}}^{+}$, an order isomorphism on the range $\phi :F\to L_w^p(\nu )$ and a continuous operator $S:L^p(\eta )\to E$ such that the following diagram commutes:

  

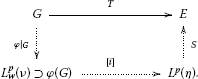
Proof First, remark that $F_a=F_{an}$ due to the Fatou property of F. Let us show $\text{(1)}\to \text{(2)}$. The existence of the vector measure on a δ-ring and the order isomorphism $\phi :F\to L_w^p(\nu )$ are direct consequences of Theorem 1. So, we can apply $\text{(1)}\to \text{(2)}$ in Theorem 4 to the subspace $\phi (G)$ that satisfies $L^p(\nu )\subset \phi (G)\subset L_w^p(\nu )$. Note that $T\circ {\phi }^{-1}{|}_{L^p(\nu )}$ is also p-concave. This gives the measure $\eta :\mathcal{R}\to {\mathbb{R}}^{+}$ satisfying that

$$\parallel (T\circ {\phi }^{-1})(f)\parallel \le {(\int {|f|}^{p}d\eta )}^{\frac{1}{p}}<+\mathrm{\infty },f\in \phi (G).$$

If $f=\phi (x)$ with $x\in G$, we obtain the inequality in (2).

The implication $\text{(2)}\to \text{(3)}$ is given by $\text{(2)}\to \text{(3)}$ in Theorem 4 composing also with φ. Finally, $\text{(3)}\to \text{(1)}$ is given directly by Theorem 4. □

Remark 7 To finish the paper, let us report that the main requirements in Theorem 4 - density of the σ-order continuous part together with T being a Fatou operator - are necessary, which means that in some sense this result is optimal.

• (1) A simple counterexample that proves that the order density of the σ-order continuous part is necessary is a functional $\varphi \ge 0$ in ${(L^{\mathrm{\infty }}[0,1])}^{\ast }$ not belonging to $L^1[0,1]$. The σ-order continuous part of $L^{\mathrm{\infty }}[0,1]$ is trivial, the operator ϕ is obviously p-concave and $L^{\mathrm{\infty }}[0,1]$ is p-convex for every $1\le p$. Since ${(L^{\mathrm{\infty }}[0,1])}_{[p]}=L^{\mathrm{\infty }}[0,1]$, the factorization would mean that $\varphi \in L^1[0,1]$ just using the domination by the measure and the Radon-Nikodým theorem, which gives a contradiction. Notice that ϕ is trivially a Fatou operator.

• (2) A bit more elaborated example is the following. Consider ${\ell }^{\mathrm{\infty }}(\mathrm{\Gamma })$, where Γ is an uncountable set, and let a functional $\varphi :{\ell }^{\mathrm{\infty }}(\mathrm{\Gamma })\to \mathbb{R}$ with ϕ not belonging to ${\ell }^1(\mathrm{\Gamma })={(c_0(\mathrm{\Gamma }))}^{\ast }=ca(\mathrm{\Gamma })$. Recall that ${({\ell }^{\mathrm{\infty }}(\mathrm{\Gamma }))}^{\ast }=ca(\mathrm{\Gamma })\oplus pa(\mathrm{\Gamma })$, where $ca(\mathrm{\Gamma })$ is the space of the countably additive measures and $pa(\mathrm{\Gamma })$ is the space of the purely finite additive measures (see, for example, Corollary 13.11, Section 9.10 and Section 9.11 in [30]). Let $P_1$ be the projection of ${({\ell }^{\mathrm{\infty }}(\mathrm{\Gamma }))}^{\ast }$ on $ca(\mathrm{\Gamma })$. We have that ${\varphi }_1:=\varphi -P_1(\varphi )\ne 0$. Since ${\varphi }_1$ is not countably additive, there is a sequence ${(A_i)}_{i=1}^{\mathrm{\infty }}$ of measurable sets such that ${\sum }_{i=1}^{\mathrm{\infty }}{\varphi }_1({\chi }_{A_i})\ne {\varphi }_1({\chi }_{{\bigcup }_{i=1}^{\mathrm{\infty }}{A}_i})$. Let us define now $T:c_0(\mathrm{\Gamma })+span\{{\chi }_{\mathrm{\Gamma }};{\chi }_{A_i},i\in \mathbb{N}\}\to \mathbb{R}$ given by $T(\cdot ):={\varphi }_1(\cdot )$. The operator T is clearly p-concave, but T is not Fatou, which can be proved using an argument similar to the one given in Example 3. Moreover, T cannot be bounded by an integral; otherwise, ${\varphi }_1$ would be countably additive.