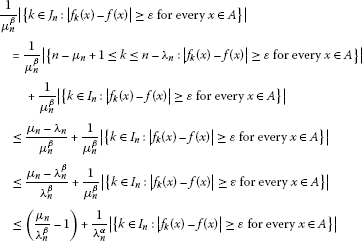- Research
- Open access
- Published:
On λ-statistical convergence of order α of sequences of function
Journal of Inequalities and Applications volume 2013, Article number: 204 (2013)
Abstract
In this study we introduce the concept of -statistical convergence of sequences of real valued functions. Also some relations between -statistical convergence and strong -summability are given.
MSC:40A05, 40C05, 46A45.
1 Introduction
The idea of statistical convergence was given by Zygmund [1] in the first edition of his monograph published in Warsaw in 1935. The concept of statistical convergence was introduced by Steinhaus [2] and Fast [3] and then reintroduced by Schoenberg [4] independently. Over the years and under different names, statistical convergence has been discussed in the theory of Fourier analysis, ergodic theory, number theory, measure theory, trigonometric series, turnpike theory and Banach spaces. Later on, it was further investigated from the sequence space point of view and linked with summability theory by Connor [5], Edely et al. [6], Et et al. [7–10], Fridy [11], Güngör et al. [12–14], Kolk [15], Orhan et al. [16, 17], Mursaleen [18], Kumar and Mursaleen [19], Rath and Tripathy [20], Salat [21], Savaş [22] and many others. In recent years, generalizations of statistical convergence have appeared in the study of strong integral summability and the structure of ideals of bounded continuous functions on locally compact spaces. Statistical convergence and its generalizations are also connected with subsets of the Stone-Čech compactification of the natural numbers. Moreover, statistical convergence is closely related to the concept of convergence in probability.
In the present paper, we introduce and examine the concepts of pointwise λ-statistical convergence of order α and pointwise -summability of order α of sequences of real valued functions. In Section 2, we give a brief overview about statistical convergence and strong p-Cesàro summability. In Section 3, we establish some inclusion relations between and and between and .
2 Definition and preliminaries
The definitions of statistical convergence and strong p-Cesàro convergence of a sequence of real numbers were introduced in the literature independently of one another and followed different lines of development since their first appearance. It turns out, however, that the two definitions can be simply related to one another in general and are equivalent for bounded sequences. The idea of statistical convergence depends on the density of subsets of the set ℕ of natural numbers. The density of a subset E of ℕ is defined by

where is the characteristic function of E. It is clear that any finite subset of ℕ has zero natural density and .
The α-density of a subset E of ℕ was defined by Çolak [23]. Let α be a real number such that . The α-density of a subset E of ℕ is defined by
where denotes the number of elements of E not exceeding n.
It is clear that any finite subset of ℕ has zero α density and does not hold for in general, the equality holds only if . Note that the α-density of any set reduces to the natural density of the set in case .
The order of statistical convergence of a sequence of numbers was given by Gadjiev and Orhan in [24] and after then statistical convergence of order α and strong p-Cesàro summability of order α studied by Çolak [23, 25] and generalized by Çolak and Asma [26].
Let be a nondecreasing sequence of positive real numbers tending to ∞ such that , . The generalized de la Vallée-Poussin mean is defined by , where for . A sequence is said to be -summable to a number ℓ if as [27]. If , then -summability is reduced to Cesàro summability. By Λ we denote the class of all nondecreasing sequence of positive real numbers tending to ∞ such that , .
Throughout the paper, unless stated otherwise, by ‘for all ’ we mean ‘for all except finite numbers of positive integers’ where for some .
Let A be any non empty set, by we denote the class of all bounded real valued functions defined on A.
3 Main results
In this section we give the main results of this paper. In Theorem 3.3, we give the inclusion relations between the sets of -statistically convergent sequences for different and . In Theorem 3.6, we give the relationship between the strong -summability and the strong -summability. In Theorem 3.9, we give the relationship between the strong -summability and -statistical convergence.
Definition 3.1 Let the sequence be as above and be any real number. A sequence of functions is said to be -statistical convergence (or pointwise λ-statistically convergent of order α) to the function f on a set A if, for every ,
where and denote the α th power of , that is . In this case, we write on A. means that for every and , there is an integer N such that
for all () and for each . The set of all pointwise λ-statistically convergent function sequences of order α will be denoted by . In this case, we write on A. For for all , we shall write instead of and in the special case , we shall write instead of .
The -statistical convergence is well defined for , but it is not well defined for in general. Let us define the sequence as follows:
then both
and
for , and so -statistically converges both to 2 and 0, i.e. and . But this is impossible.
Definition 3.2 Let the sequence be as above, be any real number and let p be a positive real number. A sequence of functions is said to be strongly -summable (or pointwise -summable of order α), if there is a function f such that
In this case, we write on A. The set of all strongly -summable sequences of function will be denoted by . For for all , we shall write instead of and in the special case , we shall write instead of .
Theorem 3.3 Let and be two sequences in Λ such that for all , and be a sequence of real valued functions defined on a set A.
-
(i)
If
then ;
-
(ii)
If
then .
Proof (i) Suppose that for all and let (1) be satisfied. Then and so that we may write
and so

for all , where . Now taking the limit as in the last inequality and using (1), we get .
-
(ii)
Let on A and (2) be satisfied. Since , for , we may write
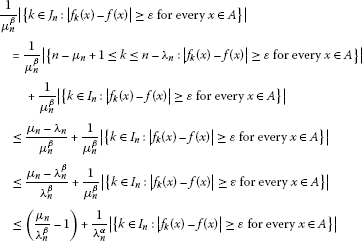
for all . Since by (2) the first term and since on A, the second term of right-hand side of above inequality tends to 0 as . (Note that for all .) This implies that . □
From Theorem 3.3, we have the following results.
Corollary 3.4 Let and be two sequences in Λ such that for all and be a sequence of real valued functions defined on a set A. If (1) holds then,
-
(i)
, for each and for all ;
-
(ii)
, for each and for all ;
-
(iii)
for all .
Corollary 3.5 Let and be two sequences in Λ such that for all and be a sequence of real valued functions defined on a set A. If (2) holds then,
-
(i)
for each and for all ;
-
(ii)
, for each and for all ;
-
(iii)
for all .
Theorem 3.6 Given for , suppose that for all , and be a sequence of real valued functions defined on a set A. Then
-
(i)
If (1) holds then for all ;
-
(ii)
If (2) holds and let , then for all .
Proof (i) Omitted.
-
(ii)
Let and suppose that (2) holds. Since , then there exists some such that for all and for all . Now, since and for all , we may write
for every . Therefore, . □
From Theorem 3.6, we have the following results.
Corollary 3.7 Let and be two sequences in Λ such that for all and be a sequence of real valued functions defined on a set A. If (1) holds then:
-
(i)
, for each and for all ;
-
(ii)
, for each and for all ;
-
(iii)
for all .
Corollary 3.8 Let and be two sequences in Λ such that for all and be a sequence of real valued functions defined on a set A. If (2) holds then:
-
(i)
, for each and for all ;
-
(ii)
, for each and for all ;
-
(iii)
for all .
Theorem 3.9 Let α and β be fixed real numbers such that , , for all and be a sequence of real valued functions defined on a set A. Then:
-
(i)
Let (1) holds, if a sequence of real valued functions defined on a set A is strongly -summable to f, then it is -statistically convergent to f;
-
(ii)
Let (2) holds, and be a sequence of bounded real valued functions defined on a set A, if a sequence is -statistically convergent to f then it is strongly -summable to f.
Proof (i) For any function sequence and , we have
and so that
Since (1) holds, it follows that if is strongly -summable to f, then it is -statistically convergent to f.
-
(ii)
Suppose that and . Then there exists some such that for all k, then for every we may write
for all . Using (2), we obtain that , whenever . □
From Theorem 3.9, we have the following results.
Corollary 3.10 Let and be two sequences in Λ such that for all and be any real number. If (1) holds, then:
-
(i)
If a sequence of real valued functions defined on a set A is strongly -summable to f, then it is -statistically convergent to f;
-
(ii)
If a sequence of real valued functions defined on a set A is strongly -summable to f, then it is -statistically convergent to f;
-
(iii)
If a sequence of real valued functions defined on a set A is strongly -summable to f, then it is -statistically convergent to f.
Corollary 3.11 Let and be two sequences in Λ such that for all , be any real number. If (2) holds, then:
-
(i)
If a sequence of bounded real valued functions defined on a set A is -statistically convergent to f, then it is strongly -summable to f;
-
(ii)
If a sequence of bounded real valued functions defined on a set is -statistically convergent to f, then it is strongly -summable to f;
-
(iii)
If a sequence of bounded real valued functions defined on a set A is -statistically convergent to f, then it is strongly -summable to f.
References
Zygmund A: Trigonometric Series. Cambridge University Press, Cambridge; 1979.
Steinhaus H: Sur la convergence ordinaire et la convergence asymptotique. Colloq. Math. 1951, 2: 73–74.
Fast H: Sur la convergence statistique. Colloq. Math. 1951, 2: 241–244.
Schoenberg IJ: The integrability of certain functions and related summability methods. Am. Math. Mon. 1959, 66: 361–375. 10.2307/2308747
Connor JS: The statistical and strong p -Cesàro convergence of sequences. Analysis 1988, 8: 47–63.
Edely OHH, Mohiuddine SA, Noman AK: Korovkin type approximation theorems obtained through generalized statistical convergence. Appl. Math. Lett. 2010, 23(11):1382–1387. 10.1016/j.aml.2010.07.004
Et M, Nuray F:-statistical convergence. Indian J. Pure Appl. Math. 2001, 32(6):961–969.
Et M: Strongly almost summable difference sequences of order m defined by a modulus. Studia Sci. Math. Hung. 2003, 40(4):463–476.
Et M: Spaces of Cesàro difference sequences of order r defined by a modulus function in a locally convex space. Taiwan. J. Math. 2006, 10(4):865–879.
Et M, Altin Y, Choudhary B, Tripathy BC: On some classes of sequences defined by sequences of Orlicz functions. Math. Inequal. Appl. 2006, 9(2):335–342.
Fridy J: On statistical convergence. Analysis 1985, 5: 301–313.
Gökhan A, Güngör M: On pointwise statistical convergence. Indian J. Pure Appl. Math. 2002, 33(9):1379–1384.
Güngör M, Et M, Altn Y:Strongly -summable sequences defined by Orlicz functions. Appl. Math. Comput. 2004, 157(2):561–571. 10.1016/j.amc.2003.08.051
Güngör M, Et M: -strongly almost summable sequences defined by Orlicz functions. Indian J. Pure Appl. Math. 2003, 34(8):1141–1151.
Kolk E: The statistical convergence in Banach spaces. Acta Comment. Univ. Tartu Math. 1991, 928: 41–52.
Duman O, Orhan C: μ -statistically convergent function sequences. Czechoslov. Math. J. 2004, 54(129)(2):413–422.
Miller HI, Orhan C: On almost convergent and statistically convergent subsequences. Acta Math. Hung. 2001, 93(1–2):135–151.
Mursaleen M: λ -statistical convergence. Math. Slovaca 2000, 50(1):111–115.
Kumar V, Mursaleen M: On -statistical convergence of double sequences on intuitionistic fuzzy normed spaces. Filomat 2011, 25(2):109–120. 10.2298/FIL1102109K
Rath D, Tripathy BC: On statistically convergent and statistically Cauchy sequences. Indian J. Pure Appl. Math. 1994, 25(4):381–386.
Šalát T: On statistically convergent sequences of real numbers. Math. Slovaca 1980, 30: 139–150.
Savaş E: Strong almost convergence and almost λ -statistical convergence. Hokkaido Math. J. 2000, 29(3):531–536.
Çolak R: Statistical Convergence of Order α. Modern Methods in Analysis and Its Applications. Anamaya Pub., New Delhi; 2010:121–129.
Gadjiev AD, Orhan C: Some approximation theorems via statistical convergence. Rocky Mt. J. Math. 2002, 32(1):129–138. 10.1216/rmjm/1030539612
Çolak R: On λ -statistical convergence. Conference on Summability and Applications 2011.
Çolak R, BektaşÇ A: λ -statistical convergence of order α . Acta Math. Sci. 2011, 31(3):953–959.
Leindler L: Über die la Vallee-Pousinsche Summierbarkeit Allgemeiner Orthogonalreihen. Acta Math. Acad. Sci. Hung. 1965, 16: 375–387. 10.1007/BF01904844
Acknowledgements
Dedicated to Professor Hari M Srivastava.
The authors would like to thank the Management Union of the Scientific Research Projects of Frat University for its financial support under a grant with number FUBAP . Also, the authors wish to thank the referees for their careful reading of the manuscript and valuable of the manuscript and valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
ME, MÇ and MK have contributed to all parts of the article.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Et, M., Çınar, M. & Karakaş, M. On λ-statistical convergence of order α of sequences of function. J Inequal Appl 2013, 204 (2013). https://doi.org/10.1186/1029-242X-2013-204
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-204