On periodic one-parameter groups of linear operators in a Banach space and applications

Abstract

Let D be the infinitesimal generator of a strongly continuous periodic one-parameter group of linear operators in a Banach space. Main results: An analog of the resolvent operator (= quasi-resolvent operator of D) is defined for points of the spectrum of D and its evident form is given. The theorem on integral for the operator D, theorems on the existence of periodic solutions of a linear differential equation of the n th order with constant coefficients and systems of linear differential equations with constant coefficients in Banach spaces are obtained. In the case of the existence of periodic solutions, evident forms of all periodic solutions of a linear differential equation of the n th order with constant coefficients and systems of linear differential equations with constant coefficients in Banach spaces are given in terms of resolvent and quasi-resolvent operators of D.

MSC:42A, 43, 47D.

1 Introduction

One-parameter groups of linear operators and periodic one-parameter groups of linear operators in topological vector spaces were investigated by Stone [1], Dunford [2], Gelfand [3] and others (see [4–20]).

Let T be the one-dimensional torus $\{e^{it}:-\pi \le t<\pi \}$. Further we consider T as the additive group $Q/2\pi Z\simeq \{t:-\pi \le t<\pi \}$ with its Euclidean topology, where Q is the field of real numbers. Let $\alpha (t)$ ($t\in T$) be a strongly continuous one-parameter group of bounded linear operators in a Banach space H, and let D be an infinitesimal generator of the group $\alpha (t)$. The evident form of the resolvent operator $R(\mu ,D)$ of D is known (see [7], Lemma 2.25)

$$R(\mu ,D)={(1-e^{-\mu t})}^{-1}{\int }_0^{2\pi }{e}^{-\mu t}\alpha (t)xdt,$$

where μ is an element of the resolvent set of D. For the element μ of the resolvent set of D and arbitrary element $a\in H$, the element $R(\mu ,D)a$ is the evident form of the unique solution of the equation $Dx-\mu x=a$.

In the present paper, we obtain conditions of the existence of a solution of the equation $Dx-\mu x=a$ for points of the spectrum of D. We define an analog of the resolvent operator (= quasi-resolvent operator) for points of the spectrum of D and, in the case of the existence of a solution, we give the evident form of all solutions by using a quasi-resolvent operator of D. We apply resolvent and quasi-resolvent operators to a solution of a linear differential equation $P(D)x=a$ of the n th order with constant coefficients and to a system of linear differential equations of the first order with constant coefficients in a Banach space H.

Contents of the present paper is the following. In Section 2 we give generalizations of Fejer’s theorem and Riemann-Lebesque’s lemma for a strongly continuous linear representation of T in a Banach space. These results are used in the next sections.

In Section 3 we give a definition of the infinitesimal generator D of a strongly continuous linear representation of T in a Banach space H and the domain $H(D)$ of the definition of D. For D and any $\lambda \in C$, we introduce the operator $R_{\lambda }:H\to H$ by formula (1) below for the point λ of the resolvent set of D and by (2) for the point of the spectrum of D. We show that the linear operator $R_{\lambda }$ is bounded and has properties (3) and (4) below.

In Section 4 we prove that $H(D)=R_{\lambda }(H)$ for all $\lambda \in C$, the spectrum $\sigma (D)$ of the operator D is a point spectrum and $\sigma (D)=\{im\in Spec(H)\}$, where $Spec(H)$ is the spectrum of the linear representation α. It is proved that $R_{\lambda }$ is equal to the resolvent operator of D for all points λ of the resolvent set of D. We obtain the theorem on an integral for D.

In Section 5 we give conditions of the existence of a periodic solution of a linear differential equation of the n th order with constant coefficients. In the case of existence, the evident form of all periodic solutions is given.

In Section 6 we give conditions of the existence of a periodic solution of a system of linear differential equations of the first order with constant coefficients. In the case of existence, the evident form of all periodic solutions is given.

For simplicity, we prove our main results for an isometric strongly continuous linear representation. But they are true for any strongly continuous linear representation.

2 Fejer’s theorem and Riemann-Lebesque’s lemma for a strongly continuous linear representation of T in a Banach space

Denote the group of all invertible bounded linear operators $A:H\to H$ of a complex Banach space H by $\mathit{GL}(H)$. The following Definitions 1-4 are known [21].

Definition 1 A homomorphism $\alpha :T\to \mathit{GL}(H)$ is called a linear representation of T on a Banach space H.

Definition 2 Linear representations $\alpha :T\to \mathit{GL}(H)$ and $\beta :T\to \mathit{GL}(V)$ are called equivalent if there exists a bounded invertible linear operator $B:H\to V$ such that $B\alpha (t)=\beta (t)B$ for all $t\in T$.

Definition 3 A linear representation α of T on a Banach space H is called isometric if $\parallel \alpha (t)x\parallel =\parallel x\parallel$ for all $t\in T$ and $x\in H$.

Definition 4 A linear representation α of T on a Banach space H is called strongly continuous if ${lim}_{t\to 0}\alpha (t)x=x$ for all $x\in H$.

It is known that every strongly continuous linear representation of T on a Banach space is equivalent to a strongly continuous isometric linear representation of T on a Banach space [21].

Let α be a strongly continuous linear representation of T on a Banach space H, and let Z be the ring of all integers and $n\in Z$. Put

$$H_n:=\{x\in H:\alpha (t)x=e^{int}x\mathrm{\forall }t\in T\}.$$

Let $x\in H$ and $n\in Z$. By the theorem in ([22], p.314), Riemann’s integral

$$F_n(x):=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{e}^{-int}\alpha (t)xdt$$

exists and $F_n(x)\in H_n$.

Proposition 1 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then

• 1.
  $$\alpha (t)F_n(x)=F_n(\alpha (t)x)=e^{int}{F}_n(x)$$

  for all $n\in Z$, $x\in H$ and $t\in T$;

• 2.
  $$F_n\cdot F_m=0$$

  and $F_n^2=F_n$ for all $m,n\in Z$, $m\ne n$;

• 3.
  $$\parallel F_n(x)\parallel \le \parallel x\parallel$$

  for all $n\in Z$ and $x\in H$.

Proof It is easy, so it is omitted. □

A series in the form ${\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}{x}_k$, $x_k\in H_k$, is called the Fourier series of an element $x\in H$, if $x_k=F_k(x)$ for all $k\in Z$. It is written in the form

$$x\sim \sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{x}_k\text{or}x\sim \sum _{k=-\mathrm{\infty }}^{k=\mathrm{\infty }}{F}_k(x).$$

For $x\in H$ and for an integer number $n\ge 0$, let us put

$$H_f$$

is a subspace of H.

In the present paper, we assume that $Spec(H)$ is infinite. The case of the finite $Spec(H)$ is investigated easy and it is omitted.

Theorem 1 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then ${lim}_{n\to \mathrm{\infty }}{\psi }_n(x)=x$ for every $x\in H$ and $\overline{H_f}=H$.

Proof

In a standard manner, we obtain the equality

$${\psi }_n(x)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{K}_n(t)\alpha (t)xdt.$$

Since ${lim}_{t\to 0}\alpha (t)x=x$, for every $\epsilon >0$, there exists $\delta >0$ such that $0<\delta$ $<\frac{\pi }{2}$ and $\parallel \alpha (t)x-x\parallel <\frac{\epsilon }{2}$ for all $t\in (-\delta ,\delta )$. We have

$$K_n(t)=\frac{1}{n+1}{\left(\frac{sin\frac{(n+1)}{2}t}{sin\frac{t}{2}}\right)}^2\le \frac{1}{(n+1){sin}^2\frac{\delta }{2}}$$

for all $t\in [\delta ,\pi ]$. Since α is a strongly continuous isometric linear representation, $K_n(t)=K_n(-t)$ for all $t\in [-\pi ,\pi ]$, $\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{K}_n(t)dt=1$ and $sin\frac{\delta }{2}\le sin\frac{t}{2}$ for all $t\in [\delta ,\pi )$, it follows that

$$\begin{array}{rcl}\parallel {\psi }_n(x)-x\parallel & =& \parallel \frac{1}{2\pi }{\int }_{-\pi }^{\pi }{K}_n(t)\alpha (t)xdt-\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{K}_n(t)xdt\parallel \\ \le & \frac{1}{2\pi }{\int }_{-\pi }^{-\delta }\parallel K_n(t)(\alpha (t)x-x)\parallel dt+\frac{1}{2\pi }{\int }_{-\delta }^{\delta }\parallel K_n(t)(\alpha (t)x-x)\parallel dt\\ +\frac{1}{2\pi }{\int }_{\delta }^{\pi }\parallel K_n(t)(\alpha (t)x-x)\parallel dt\\ \le & \frac{1}{\pi }{\int }_{\delta }^{\pi }\parallel K_n(t)\parallel \parallel \alpha (t)x-x\parallel dt+\frac{1}{2\pi }{\int }_{-\delta }^{\delta }\parallel K_n(t)\parallel \parallel \alpha (t)x-x\parallel dt\\ \le & \frac{1}{\pi (n+1){sin}^2\frac{\delta }{2}}{\int }_{\delta }^{\pi }\parallel \alpha (t)x-x\parallel dt+\frac{1}{2\pi }{\int }_{-\delta }^{\delta }{K}_n(t)\epsilon dt\\ \le & \frac{2\parallel x\parallel }{(n+1){sin}^2\frac{\delta }{2}}+\frac{\epsilon }{2\pi }.\end{array}$$

Hence ${lim}_{n\to \mathrm{\infty }}{\psi }_n(x)=x$. This, in view of ${\psi }_n(x)\in H_f$ for all n, implies that $\overline{H_f}=H$. □

Remark 1 Theorem 1 is known for the homogeneous Banach spaces on T ([6], p.87; [23], pp.14-15). For a strongly continuous linear representation of T in a locally convex space, it is obtained in [10].

Corollary 1 Let α be a strongly continuous isometric linear representation of T on a Banach space H and $x,y\in H$. If $F_n(x)=F_n(y)$ for each $n\in Z$, then $x=y$.

Proof Since $F_n(x)=F_n(y)$ for each $n\in Z$, it follows that ${\psi }_n(x)={\psi }_n(y)$ for each $n\in Z$. Hence Theorem 1 gives $x=y$. □

Theorem 2 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then ${lim}_{n\to \mathrm{\infty }}{F}_n(x)=0$ for each $x\in H$.

Proof Let $\epsilon >0$ be given. Since ${lim}_{t\to 0}\alpha (t)x=x$, there exists a natural number $N(\epsilon )$ such that $\parallel \alpha (-\frac{\pi }{n})x-x\parallel <\epsilon$ for all natural numbers $n\ge N(\epsilon )$. Since

$$F_n(x)=\frac{1}{2\pi }{\int }_{-\pi +\frac{\pi }{n}}^{\pi +\frac{\pi }{n}}{e}^{-int}\alpha (t)xdt=-\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{e}^{-int}\alpha (t+\frac{\pi }{n})xdt,$$

we have

$$F_n(x)=\frac{1}{4\pi }{\int }_{-\pi }^{\pi }{e}^{-int}\alpha (t+\frac{\pi }{n})(\alpha (-\frac{\pi }{n})x-x)dt.$$

So, $\parallel F_n(x)\parallel \le \parallel \alpha (-\frac{\pi }{n})(x)-x\parallel <\epsilon$ for all $n\ge N(\epsilon )$. □

Remark 2 This theorem is a generalization of Riemann-Lebesque’s lemma ([23], p.13).

3 The operator $R_{\lambda }$

Let α be a strongly continuous isometric linear representation of T on a Banach space H.

Definition 5 ([7], p.45)

A point $x\in H$ is called a differentiable point of α if there exists

$$Dx:=\underset{t\to 0}{lim}\frac{\alpha (t)x-x}{t}\text{in }H.$$

Denote the set of all differentiable points of α by $H(D)$. The set $Spec(H)$ is called the spectrum of D. The set $C\setminus Spec(H)$ is called the resolvent set of D.

Proposition 2 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then

• (i)
  $$H(D)$$

  is a linear subspace of H, $H_f\subset H(D)$ and $\overline{H(D)}=H$;

• (ii)
  $$H(D)$$

  is $\alpha (T)$-invariant and $\alpha (t)Dx=D\alpha (t)x$ for all $t\in T$, $x\in H(D)$;

• (iii)
  $$D{F}_n(x)=F_n(Dx)=in{F}_n(x)$$

  for all $n\in Z$ and $x\in H(D)$.

Proof (i) It is obvious that $H(D)$ is a linear subspace of H. Let $x\in H_f$. Then x can be expressed in the form ${\sum }_{\ell =-m}^m{F}_{\ell }(x)$ for some m. Since $F_{\ell }(x)\in H_{\ell }$, we get

$$\underset{t\to 0}{lim}\frac{\alpha (t)x-x}{t}=\underset{t\to 0}{lim}\sum _{\ell =-m}^m\left(\frac{e^{i\ell t}-1}{t}\right)F_{\ell }(x)=\sum _{\ell =-m}^{m}i\ell F_{\ell }(x).$$

Hence $x\in H(D)$ and $Dx={\sum }_{\ell =-m}^{m}i\ell F_{\ell }(x)$. Therefore $H_f\subset H(D)$. By Theorem 1 $\overline{H_f}=\overline{H(D)}=H$.

• (ii) Let $x\in H(D)$. Since $\alpha (t)$ is strongly continuous, we have

  $$\alpha (t)Dx=\alpha (t)\underset{s\to 0}{lim}\frac{\alpha (s)x-x}{s}=\underset{s\to 0}{lim}\frac{\alpha (s)\alpha (t)x-\alpha (t)x}{s}=D\alpha (t)x.$$

Hence $\alpha (t)x\in H(D)$ and $\alpha (t)Dx=D\alpha (t)x$.

• (iii) Let $n\in Z$ and $x\in H(D)$. Using the continuity of $F_n$ and Proposition 1, we get

  $$D{F}_n(x)=F_n(Dx)=\underset{t\to 0}{lim}\frac{e^{int}{F}_n(x)-F_n(x)}{t}=in{F}_n(x).$$

 □

Remark 3 It is easily seen that $H=H(D)$ if and only if $Spec(H)$ is finite.

Definition 6 The operator D is called an infinitesimal generator of a linear representation α (see [7], p.45).

Proposition 3 Let $x\in H(D)$. Then the function $G_x(t):=\alpha (t)x$ is differentiable on T and $G_x^{\prime }(t)=\alpha (t)G_x^{\prime }(0)=\alpha (t)Dx$.

Proof Since α is strongly continuous, we have

$$G_x^{\prime }(t)=\underset{s\to 0}{lim}\frac{\alpha (t+s)x-\alpha (t)x}{s}=\alpha (t)\underset{s\to 0}{lim}\frac{\alpha (s)x-x}{s}=\alpha (t)Dx.$$

 □

Let α be a strongly continuous isometric linear representation of T on a Banach space H. For any $x\in H$ and $\lambda \in C$, there exists the following vector-valued Riemann’s integral:

$${\int }_0^{2\pi }{e}^{\lambda t}({\int }_0^t{e}^{-\lambda s}\alpha (s)xds)dt.$$

We consider linear operators $R_{\lambda }$ on H defined by

$$R_{\lambda }(x)=\frac{\lambda }{1-e^{2\pi \lambda }}{\int }_0^{2\pi }{e}^{\lambda t}({\int }_0^t{e}^{-\lambda s}\alpha (s)xds)dt+\frac{1}{2\pi (1-e^{2\pi \lambda })}{\int }_0^{2\pi }\alpha (t)xdt$$

(1)

for all $\lambda \in C$ such that $\lambda \ne im$, $m\in Z$ and

$$R_{im}(x)=\frac{1+\pi }{2\pi }{\int }_0^{2\pi }{e}^{-imt}\alpha (t)xdt-\frac{1}{2\pi }{\int }_0^{2\pi }({\int }_0^t{e}^{-ims}\alpha (s)xds)dt$$

(2)

for all $m\in Z$. In Theorem 4(iv) below, we prove that $R_{\lambda }$ is equal to the resolvent operator of D for every point λ of the resolvent set of D. The operator $R_{im}(x)$ is called the quasi-resolvent operator of D for the point im of the spectrum of D. The operator $R_{\lambda }$ was introduced in [9, 13].

Theorem 3 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then

• (i) the operator $R_{\lambda }$, defined by (1) and (2), is bounded for all $\lambda \in C$;

• (ii)
  $$R_{\lambda }(F_n(x))=F_n(R_{\lambda }(x))=\frac{1}{in-\lambda }{F}_n(x)$$

  (3)

for all $\lambda \ne in$, $\lambda \in C$, $n\in Z$;

• (iii)
  $$R_{in}(F_n(x))=F_n(R_{in}(x))=F_n(x)$$

  (4)

for all $n\in Z$ and $x\in H$;

• (iv)
  $$R_{\lambda }{R}_{\mu }(x)=R_{\mu }{R}_{\lambda }(x)$$

  for all $x\in H$.

Proof (i) Let $L:={\int }_0^{2\pi }\parallel e^{\lambda t}\parallel ({\int }_0^t\parallel e^{-\lambda s}\parallel ds)dt$. Then it is obvious that

$$\parallel R_{\lambda }(x)\parallel \le \{\begin{array}{cc}\frac{(\parallel \lambda \parallel L+1)}{\parallel 1-e^{2\pi \lambda }\parallel }\parallel x\parallel \hfill & \text{if }\lambda \in C\text{ and }\lambda \ne im,m\in Z,\hfill \\ (1+2\pi )\parallel x\parallel \hfill & \text{if }\lambda =im,m\in Z.\hfill \end{array}$$

Therefore $R_{\lambda }$ is bounded in H for all $\lambda \in C$.

• (ii) Let $x\in H_f$, $\lambda \in C$ and $\lambda \ne im$ for all $m\in Z$. Then $x={\sum }_{\ell =-k}^k{F}_{\ell }(x)$ for some k. Since $F_{\ell }(x)\in H_{\ell }$, using Proposition 1, we get

  $$\begin{array}{rcl}{R}_{\lambda }(x)& =& \frac{\lambda }{1-e^{2\pi \lambda }}{\int }_0^{2\pi }{e}^{\lambda t}\left({\int }_0^t{e}^{-\lambda s}(\sum _{\ell =-k}^k\alpha (s)F_{\ell }(x))ds\right)dt\\ +\frac{1}{2\pi (1-e^{2\pi \lambda })}{\int }_0^{2\pi }(\sum _{\ell =-k}^k\alpha (t)F_{\ell }(x))dt\\ =& \frac{\lambda }{1-e^{2\pi \lambda }}{\int }_0^{2\pi }{e}^{\lambda t}(\sum _{\ell =-k}^k{\int }_0^t{e}^{(i\ell -\lambda )s}{F}_{\ell }(x)ds)dt\\ +\frac{1}{2\pi (1-e^{2\pi \lambda })}{\int }_0^{2\pi }\sum _{\ell =-k}^k{e}^{i\ell t}{F}_{\ell }(x)dt\\ =& \frac{\lambda }{1-e^{2\pi \lambda }}\sum _{\ell =-k}^k{\int }_0^{2\pi }\frac{e^{i\ell t}}{i\ell -\lambda }{F}_{\ell }(x)dt-\frac{\lambda }{1-e^{2\pi \lambda }}\sum _{\ell =-k}^k{\int }_0^{2\pi }\frac{e^{\lambda t}}{i\ell -\lambda }{F}_{\ell }(x)dt\\ +\frac{1}{2\pi (1-e^{2\pi \lambda })}\sum _{\ell =-k}^k{\int }_0^{2\pi }{e}^{i\ell t}{F}_{\ell }(x)dt\\ =& \frac{1}{e^{2\pi \lambda }-1}{F}_0(x)+\sum _{\ell =-k}^k\frac{1}{i\ell -\lambda }{F}_{\ell }(x)-\frac{1}{e^{2\pi \lambda }-1}{F}_0(x)=\sum _{\ell =-k}^k\frac{1}{i\ell -\lambda }{F}_{\ell }(x).\end{array}$$

Hence, using $F_m\circ F_l=0$ for $l\ne m$ (Proposition 1), we get $F_n(R_{\lambda }(x))=\frac{1}{in-\lambda }{F}_n(x)=R_{\lambda }(F_n(x))$.

Let x be an arbitrary element of H. By Theorem 1, ${lim}_{p\to \mathrm{\infty }}{\psi }_p(x)=x$. Since ${\psi }_p(x)\in H_f$, we have $F_n(R_{\lambda }({\psi }_p(x)))=\frac{1}{in-\lambda }{F}_n({\psi }_p(x))$ for all $n\in Z$ and $p\in N$. On the other hand, from ${lim}_{p\to \mathrm{\infty }}{\psi }_p(x)=x$, using the continuity of operators $F_n$ and $R_{\lambda }$, we get $F_n(R_{\lambda }(x))=\frac{1}{in-\lambda }{F}_n(x)=R_{\lambda }(F_n(x))$.

Now we prove equality (3) for $\lambda =im$, $m\in Z$, $n\ne m$. Let $x\in H_f$ and $F_m(x)=0$. Then $x={\sum }_{\ell \ne m,\ell =-k}^k{F}_{\ell }(x)$ for some $k\in N$ and $\alpha (t)x={\sum }_{\ell \ne m,\ell =-k}^k{e}^{i\ell t}{F}_{\ell }(x)$. Hence

$$\begin{array}{rcl}{R}_{im}(x)& =& \frac{1+\pi }{2\pi }\sum _{\ell \ne m,\ell =-k}^k{\int }_0^{2\pi }{e}^{i(\ell -m)t}{F}_{\ell }(x)dt-\frac{1}{2\pi }{\int }_0^{2\pi }(\sum _{\ell \ne m,\ell =-k}^k{\int }_0^t{e}^{i(\ell -m)s}{F}_{\ell }(x))ds\\ =& \sum _{\ell \ne m,\ell =1}^k\frac{1}{i\ell -im}{F}_{\ell }(x).\end{array}$$

It implies that

$$\begin{array}{rcl}{R}_{im}(F_n(x))& =& F_n(R_{im}(x))=\sum _{\ell \ne m,\ell =-k}^k\frac{1}{i\ell -im}{F}_n(F_{\ell }(x))\\ =& \{\begin{array}{cc}\frac{1}{in-im}{F}_n(x),\hfill & n\ne m,\parallel n\parallel \le k,\hfill \\ 0,\hfill & n=m\text{ or }n>k.\hfill \end{array}\end{array}$$

(5)

Let $F_m(x)\ne 0$. Then x= $F_m(x)+{\sum }_{\ell \ne m,\ell =-k}^k{F}_{\ell }(x)$ for some $k\in N$. Since $F_m(x-F_m(x))=0$, using equalities (5) and (2), we have

Hence

$$\begin{array}{rcl}\sum _{\ell \ne m,\ell =-k}^k\frac{1}{i\ell -im}{F}_{\ell }(x)+F_m(x)& =& (1+\pi )F_m(x)-\frac{1}{2\pi }{\int }_0^{2\pi }({\int }_0^t{e}^{-ims}\alpha (s)(x)ds)dt\\ =& R_{im}(x).\end{array}$$

This equality implies that

$$R_{im}(F_n(x))=F_n(R_{im}(x))=\frac{1}{in-im}{F}_n(x)$$

(6)

for all $n,m\in Z$, $n\ne m$, and $R_{im}(F_m(x))=F_m(R_{im}(x))=F_m(x)$ for all $m\in Z$, $x\in H_f$.

Let x be an arbitrary element of H. By Theorem 1, ${\psi }_p(x)\in H_f$ and equality (6), we obtain

$$\begin{array}{rcl}{R}_{im}(F_n(x))& =& F_n(R_{im}(x))=\underset{p\to \mathrm{\infty }}{lim}{F}_n\left(R_{im}({\psi }_p(x))\right)=\underset{p\to \mathrm{\infty }}{lim}\frac{1}{in-im}{F}_n({\psi }_p(x))\\ =& \frac{1}{in-im}{F}_n(x)\end{array}$$

for all $n,m\in Z$, $n\ne m$, $x\in H$.

• (iii) The proof of equality (4) is similar to the proof of equality (3).

• (iv) Using (3) and (4), we obtain $F_n{R}_{\lambda }{R}_{\mu }(x)=F_n{R}_{\mu }{R}_{\lambda }(x)$ for $x\in H$, $n\in Z$, $\lambda \in C$, $\mu \in C$. Hence, by Corollary 1, we have $R_{\lambda }{R}_{\mu }(x)=R_{\mu }{R}_{\lambda }(x)$ for all $x\in H$, $\lambda \in C$, $\mu \in C$. □

Corollary 2 Let $a\in H$, $im\in Spec(H)$ and $\lambda \in C$. Then $F_m{R}_{\lambda }(a)=0$ if and only if $F_m(a)=0$.

Proof It follows easily from Theorem 3. □

Proposition 4 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then

• (i)
  $$R_{\lambda }-R_0=\lambda (R_{\lambda }\circ R_0)-\frac{1}{\lambda }{F}_0$$

  for all $\lambda \in C$, $\lambda \ne im$, $m\in Z$;

• (ii)
  $$R_{im}-R_0=im(R_{im}\circ R_0)-\frac{1}{im}{F}_0-\frac{1}{im}{F}_m$$

  for all $m\in Z$, $m\ne 0$.

Proof (i) Let $x\in H$, $\lambda \in C$ and $\lambda \ne im$, $m\in Z$. For $n\ne 0$, using Theorem 4 and $F_n{F}_0=0$, we obtain

$$\begin{array}{rcl}{F}_n(\lambda R_{\lambda }\circ R_0(x)-\frac{1}{\lambda }{F}_0(x))& =& F_n(\lambda R_{\lambda }\circ R_0(x))-\frac{1}{\lambda }{F}_n(F_0(x))=\frac{\lambda }{in(in-\lambda )}{F}_n(x)\\ =& \frac{1}{in-\lambda }{F}_n(x)-\frac{1}{in}{F}_n(x)=F_n(R_{\lambda }(x)-R_0(x)).\end{array}$$

Similarly,

$$\begin{array}{rcl}{F}_0(R_{\lambda }(x)-R_0(x))& =& -\frac{1}{\lambda }{F}_0(x)-F_0(R_0(x))=-\frac{1}{\lambda }{F}_0(F_0(x))-F_0(R_0(x))\\ =& -\frac{1}{\lambda }{F}_0(F_0(x))+F_0(\lambda R_{\lambda }\circ R_0(x))\\ =& F_0(\lambda R_{\lambda }\circ R_0(x)-\frac{1}{\lambda }{F}_0(x)).\end{array}$$

Hence $F_n(R_{\lambda }(x)-R_0(x))=F_n(\lambda R_{\lambda }\circ R_0(x)-\frac{1}{\lambda }{F}_0(x))$ for every $n\in Z$. By Corollary 1 we have $R_{\lambda }(x)-R_0(x)=\lambda R_{\lambda }\circ R_0(x)-\frac{1}{\lambda }{F}_0(x)$ for all $x\in H$, $\lambda \in C$ and $\lambda \ne im$, $m\in Z$.

A proof of (ii) is similar. □

4 The theorem on resolvent and quasi-resolvent operators

Theorem 4 Let α be a strongly continuous isometric linear representation of T on a Banach space H. Then

• (i)
  $$H(D)=R_{\lambda }(H)$$

  for all $\lambda \in C$;

• (ii)
  $$R_{im}(D-im)x=x$$

  and $(D-im)R_{im}(y)=y$ for all $im\in Spec(H)$ and $x\in H(D)$, $y\in H$ such that $F_m(x)=F_m(y)=0$;

• (iii)
  $$R_{\lambda }(D-\lambda )x=x$$

  and $(D-\lambda )R_{\lambda }(y)=y$ for all $\lambda \in C\setminus Spec(H)$ and $x\in H(D)$, $y\in H$;

• (iv)
  $$R_{\lambda }(x)={(1-e^{-2\pi \lambda })}^{-1}{\int }_0^{2\pi }{e}^{-\lambda s}\alpha (s)xds$$

  for all $\lambda \in C\setminus Spec(H)$;

• (v) the spectrum $\sigma (D)$ of D is a point spectrum and $\sigma (D)=Spec(H)$.

Proof (i) We need the following two lemmas.

Lemma 1 $D{R}_0(x)=x-F_0(x)$ for all $x\in H_f$.

Proof An element $x\in H_f$ has the form $x={\sum }_{\ell =-k}^k{F}_{\ell }(x)$ for some k. Using Theorem 3 and Proposition 2, we obtain $F_n(D{R}_0(x))=F_n(x)$ for all $n\ne 0$ and $F_0(D{R}_0(x))=0$. Hence $D{R}_0(x)=x-F_0(x)$ for any $x\in H_f$. Lemma is proved. □

Lemma 2 Let $x\in H$ such that $F_0(x)=0$. Then

$$\alpha (t)R_0(x)={\int }_0^t\alpha (s)xds+R_0(x).$$

(7)

Proof Let us define the functions $f_n,f:[0,2\pi )\to H$ by $f_n(t):=\alpha (t)R_0({\psi }_n(x))$ and $f(t):=\alpha (t)R_0(x)$. Since α is a strongly continuous isometric linear representation, we have

$$\parallel \alpha (t)x-\alpha (t){\psi }_n(x)\parallel =\parallel x-{\psi }_n(x)\parallel$$

(8)

and

$$\parallel f(t)-f_n(t)\parallel =\parallel R_0(x)-R_0({\psi }_n(x))\parallel .$$

(9)

Equality (8) implies that

$$\parallel {\int }_0^t\alpha (s)xds-{\int }_0^t\alpha (s){\psi }_n(x)ds\parallel \le 2\pi \parallel x-{\psi }_n(x)\parallel .$$

(10)

Using $F_0(x)=0$, Proposition 3, Theorem 3, $R_0({\psi }_n(x))\in H_f$, $F_0({\psi }_n(x))=F_0(x)$ and Lemma 1, we get

$$f_n^{\mathrm{\prime }}(t)=(\alpha (t)R_0{({\psi }_n(x))}^{\mathrm{\prime }}=\alpha (t)D{R}_0({\psi }_n(x))=\alpha (t)({\psi }_n(x)-F_0(x))=\alpha (t){\psi }_n(x).$$

Hence

$$f_n(t)={\int }_0^t\alpha (s){\psi }_n(x)ds+C,$$

where $C_n\in H$. Putting $t=0$, we obtain $C_n=f_n(0)=\alpha (0)R_0({\psi }_n(x))=R_0({\psi }_n(x))$ and

$$f_n(t)={\int }_0^t\alpha (s){\psi }_n(x)ds+R_0({\psi }_n(x)).$$

(11)

Using equalities (8), (9), (11) and inequality (10), we obtain

$$\begin{array}{rcl}\parallel f(t)-({\int }_0^t\alpha (s)xds+R_0(x))\parallel & =& \parallel f(t)-f_n(t)+(f_n(t)-{\int }_0^t\alpha (s)xds-R_0(x))\parallel \\ \le & \parallel f(t)-f_n(t)\parallel +\parallel {\int }_0^t\alpha (s)({\psi }_n(x)-x)ds\parallel \\ +\parallel R_0({\psi }_n(x)-x)\parallel \le 2(\pi +\parallel R_0\parallel )\parallel {\psi }_n(x)-x\parallel \end{array}$$

for all $t\in T$. Since ${lim}_{n\to \mathrm{\infty }}{\psi }_n(x)=x$, it follows that

$$f(t)={\int }_0^t\alpha (s)xds+R_0(x)$$

and Lemma 2 is proved. □

We continue the proof of the theorem.

• (i) From equality (7) we obtain that the function $f(t)$ is differentiable and $f^{\prime }(t)=\alpha (t)x$. Using Proposition 3, we have

  $$\alpha (t)x=f^{\prime }(t)=\alpha (t)f^{\prime }(0)=\alpha (t)\underset{s\to 0}{lim}\frac{\alpha (s)R_0(x)-R_0(x)}{s}=\alpha (t)D(R_0(x)).$$

Hence $R_0(x)\in H(D)$ for all $x\in H$ such that $F_0(x)=0$. Now let $x\in H$ be an arbitrary element. Since $F_0(x-F_0(x))=0$, we have $R_0(x-F_0(x))\in H(D)$. On the other hand, by Theorem 3 and Proposition 2, $R_0{F}_0(x)=F_0(x)\in H_0\subset H(D)$. Since $x=(x-F_0(x))+F_0(x)$ and $H(D)$ is a linear subspace of H, we get $R_0(x)\in H(D)$. Hence $R_0(H)\subset H(D)$.

Conversely, let $x\in H(D)$. By Proposition 2 and Theorem 3, $Dx\sim {\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}in{F}_n(x)$ and $R_0(Dx)\sim {\sum }_{n\ne 0,n=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_n(x)$. Hence $R_0(Dx)+F_0(x)\sim {\sum }_{n=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_n(x)$. Using Corollary 1 and equality (4), we get $R_0(Dx)+F_0(x)=x$, $R_0(F_0(x))=F_0(x)$ and $R_0(Dx+F_0(x))=x$. Let us put $a:=Dx+F_0(x)$. Then $R_0(a)=x$. This means that $x\in R_0(H)$, that is, $H(D)\subset R_0(H)$; and consequently $H(D)=R_0(H)$.

Now we prove that $R_0(H)=R_{im}(H)$ for all $m\in Z$. By claim (ii) of Proposition 4 and claim (iv) of Theorem 3, $R_{im}(x)=R_0(x)+im{R}_0{R}_{im}(x)-\frac{1}{im}{F}_0(x)-\frac{1}{im}{F}_m(x)$. Since $F_0(x)\in H_0$, $F_m(x)\in H_m$ and $H_f\subset H(D)=R_0(H)$, we get $R_{im}(H)\subset R_0(H)$. By Theorem 3, $R_{im}(H_f)=H_f\subset R_{im}(H)$. Claim (ii) of Proposition 4 implies that $R_0(x)=R_{im}(x)-im{R}_{im}{R}_0(x)+\frac{1}{im}{F}_0(x)+\frac{1}{im}{F}_m(x)$. Hence $R_0(H)\subset R_{im}(H)$ and $H(D)=R_{im}(H)$. Similarly, using claims (i) and (ii) of Proposition 4, we obtain $H(D)=R_{\lambda }(H)$ for all $\lambda \in C$, $\lambda \ne im$, $m\in Z$. Thus $H(D)=R_{\lambda }(H)$ for all $\lambda \in C$.

• (ii) Let $x\in H(D)$, $F_m(x)=0$. By Proposition 2, $Dx\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}ik{F}_k(x)$. Hence $Dx-imx\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}(ik-im)F_k(x)$. Using $F_m(x)=0$ and Theorem 3, we get $R_{im}(D-im)x\sim {\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_k(x)$. By Corollary 1, $R_{im}(D-im)x=x$. Thus $R_{im}(D-im)x=x$ for all $x\in H(D)$ such that $F_m(x)=0$.

Let $x\in H$, $F_m(x)=0$. Since $x\sim {\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_k(x)$, we have $R_{im}(x)\sim {\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-im}{F}_k(x)$. According to the statement (i) of this theorem, $R_{im}(x)\in H(D)$. Using Proposition 2, we get $(D-im)R_{im}(x)\sim {\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_k(x)$, and hence $(D-im)R_{im}(x)=x$. Thus $(D-im)R_{im}(x)=x$ for all $x\in H$ such that $F_m(x)=0$.

• (iii) The proof of claim (iii) is similar to the one of (ii).

• (iv) Equalities (iii) mean that $R_{\lambda }$ is the resolvent operator for all $\lambda \in C\setminus Spec(H)$. Hence equality (iv) follows from the form of the resolvent operator in ([7], Lemma 2.25).

• (v) follows from (ii) and (iii). The proof of the theorem is completed.  □

Remark 4 Equality (iv) means that for points λ of the resolvent set of D, $R_{\lambda }$ is the other form of the resolvent operator of D.

Theorem 5 Let α be a strongly continuous isometric linear representation of T on a Banach space H, $a\in H$ and $m\in Z$. Then the equation $Dx-imx=a$ has a solution if and only if $F_m(a)=0$. In the case $F_m(a)=0$, a general solution of the equation $Dx-imx=a$ has the form $x=R_{im}(a)+c$, where c is an arbitrary element of $H_m$.

Proof Suppose that the equation $Dx-imx=a$ has a solution x. By Proposition 2 we have $Dx\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}ik{F}_k(x)$ and $Dx-imx\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}(ik-im)F_k(x)$. Hence $F_m(a)=F_m(Dx-imx)=0$.

For the converse, we assume that $F_m(a)=0$. By Theorem 4 we have $(D-im)R_{im}(a)=a$. Therefore $x=R_{im}(a)$ is a solution of the equation $Dx-imx=a$. Let $y\in H$ be a solution of the equation $Dy-imy=0$. Then $Dy-imy\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}(ik-im)F_k(y)={\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}(ik-im)F_k(y)=0$. Hence $F_k(y)=0$ for all $k\ne m$, that is, $y=F_m(y)\in H_m$. On the other hand, $Dy-imy=0$ for all $y\in H_m$. Thus a general solution of the equation $Dx-imx=a$ has the form $x=R_{im}(a)+c$, where c is an arbitrary element of $H_m$. □

Remark 5 This theorem is the theorem on integral for periodic one-parameter groups of operators.

The following theorem is known (see [7], Theorem 2.26)

Theorem 6 Let α be a strongly continuous isometric linear representation of T on a Banach space H and $a\in H(D)$. Then the Fourier series of the element a is convergent to a in H.

Proof

In a standard manner, we have the equality

$$s_n(a)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{D}_n(t)\alpha (t)adt,\text{where }{D}_n(t):=\frac{sin(n+\frac{1}{2})t}{sin\frac{1}{2}t}.$$

Using $\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{D}_n(t)dt=1$, we obtain $s_n(a)-a=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{D}_n(t)(\alpha (t)a-a)dt$. Let us consider the function

$$g(t):=\frac{1}{2tg\frac{t}{2}}-\frac{1}{t}.$$

Since ${lim}_{t\to 0}g(t)=0$, defining $g(0)=0$, we obtain that $g(t)$ is a continuous function on $[-\pi ,\pi ]$. Using the equality

$$D_n(t)=\frac{sinnt}{t}+g(t)sinnt+\frac{1}{2}cosnt,$$

we get

$$\begin{array}{rcl}{s}_n(a)-a& =& \frac{1}{2\pi }{\int }_{-\pi }^{\pi }\psi (t)sinntdt+\frac{1}{2\pi }{\int }_{-\pi }^{\pi }g(t)sinnt(\alpha (t)a-a)dt\\ +\frac{1}{4\pi }{\int }_{-\pi }^{\pi }cosnt(\alpha (t)a-a)dt,\end{array}$$

(12)

where $\psi (t):=\frac{\alpha (t)a-a}{t}$ for $t\ne 0$ and $\psi (0):=D(a)$. Functions $\psi (t)$, $\alpha (t)a-a$ and $g(t)(\alpha (t)a-a)$ are continuous vector-valued functions on T. So, using Theorem 2 and equality (12), we obtain ${lim}_{n\to \mathrm{\infty }}{s}_n=a$. □

Remark 6 Our proof of this theorem differs from that in ([7], Theorem 2.26).

Corollary 3 Let α be a strongly continuous isometric linear representation of T on a Banach space H, x be an arbitrary element of H and $x\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}{x}_k$. Then the series ${\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-\lambda }{x}_k$ is convergent to $R_{\lambda }(x)$ in Hfor all $\lambda \in C\setminus Spec(H)$ and the series $x_m+{\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-m}{x}_k$ is convergent to $R_{im}(x)$ in H for all $im\in Spec(H)$.

Proof Let $\lambda \in C\setminus Spec(H)$. According to Theorem 4, we have $R_{\lambda }(x)\in H(D)$. By Theorem 6 and $R_{\lambda }(x)\sim {\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-\lambda }{x}_k$, the series ${\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-\lambda }{x}_k$ is convergent to $R_{\lambda }(x)$ in H. The proof of the second statement is similar. □

Corollary 4 Let α be a strongly continuous isometric linear representation of T in a Banach space H and $x\in H$.

• (i) Let $\lambda \in C\setminus Spec(H)$. Then $x\in H(D)$ if and only if there exists $y\in H$ such that $x={\sum }_{k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-\lambda }{F}_k(y)$;

• (ii) Let $\lambda \in Spec(H)$. Then $x\in H(D)$ if and only if there exists $y\in H$ such that $x=y_m+{\sum }_{k\ne m,k=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{ik-im}{F}_k(y)$.

The proof follows from Theorem 4, Corollary 2 and Proposition 2. □

5 Periodic solutions of the linear differential equation $P(D)x=a$of the n th order with constant coefficients

Let $\alpha (t)$ be a strongly continuous linear representation of T in a Banach space H and D be the infinitesimal generator of α. For $a\in H$, we consider a solution of the linear differential equation

$$P(D)x=a$$

(13)

in H, where

$$P(D)=c_{0}I+c_{1}D+\cdots +c_{n-1}{D}^{n-1}+D^n,$$

(14)

$$c_i\in C$$

, $i=0,\dots ,n-1$, I is the unit operator in H.

Theorem 7 Let $P(D)$ be a linear differential operator (14), $a\in H$, let ${\lambda }_1,\dots ,{\lambda }_k$ be the roots of the polynomial $P(z)$, and let $m_i$ be the multiplicity of ${\lambda }_i$, $m_1+\cdots +m_k=n$. Then

• (i) In the case ${\lambda }_1,\dots ,{\lambda }_n\notin Spec(H)$, for any $a\in H$, there exists the unique solution of equation (13) in H, and it is $x=R_{{\lambda }_1}^{m_1}\cdots R_{{\lambda }_n}^{m_k}(a)$.

• (ii) In the case ${\lambda }_1,\dots ,{\lambda }_r\in Spec(H)$ ($r>0$) and ${\lambda }_{r+1},\dots ,{\lambda }_k\notin Spec(H)$, a solution of equation (13) exists if and only if

  $$F_{i{\lambda }_1}(a)=\cdots =F_{i{\lambda }_r}(a)=0.$$

  (15)

For $a\in H$, satisfying condition (15), a general solution of equation (13) has the form

$$x=R_{{\lambda }_1}^{m_1}\cdots R_{{\lambda }_r}^{m_r}{R}_{{\lambda }_{r+1}}^{m_{r+1}}\cdots R_{{\lambda }_n}^{m_k}+b_1+\cdots +b_r,$$

(16)

where $b_i$ is an arbitrary element of $H_{i{\lambda }_i}$, $i=1,\dots ,r$.

Proof (i) $P(D)$ may be written in the form $P(D)=(D-{\lambda }_{1}I)\cdots (D-{\lambda }_{n}I)$.

Then equation (13) has the form

$$(D-{\lambda }_{1}I)\cdots (D-{\lambda }_{n}I)x=a.$$

(17)

By Theorem 4(iii),

$$R_{\lambda }(D-\lambda I)x=x$$

(18)

for all $x\in H(D)$ and $\lambda \notin Spec(H)$. Using equality (18) to equation (17), we obtain $x=R_{{\lambda }_1}\cdots R_{{\lambda }_n}a$.

• (ii) Let ${\lambda }_1,\dots ,{\lambda }_r\in Spec(H)$ ($r>0$) and ${\lambda }_{r+1},\dots ,{\lambda }_n\notin Spec(H)$. Using $R_{{\lambda }_{r+1}},\dots ,R_{{\lambda }_n}$ to (17), we obtain

  $$(D-{\lambda }_{1}I)\cdots (D-{\lambda }_{r}I)x=R_{{\lambda }_{r+1}}\cdots R_{{\lambda }_n}a.$$

  (19)

This equation we can be written in the form

$${(D-{\lambda }_{1}I)}^{m_1}\cdots {(D-{\lambda }_{k}I)}^{m_k}x=R_{{\lambda }_{r+1}}\cdots R_{{\lambda }_n}a,$$

(20)

where ${\lambda }_i\ne {\lambda }_j$ for $i\ne j$.

Lemma 3 Let $a\in H$, $\lambda \in Spec(H)$ and $m>1$. Then the equation

$${(D-\lambda I)}^{m}x=a$$

(21)

has a solution if and only if $F_{i\lambda }(a)=0$. In the case $F_{i\lambda }(a)=0$, a general solution of this equation is $x=R_{\lambda }^m(a)+b$, where b is an arbitrary element of $H_{i\lambda }$.

Proof Put $y={(D-\lambda I)}^{m-1}x$. Then equation (21) has the form $(D-\lambda I)y=a$. By Theorem 5 this equation has a solution if and only if $F_{i\lambda }(a)=0$. In the case $F_{i\lambda }(a)=0$, a general solution is $y=R_{\lambda }(a)+b_1$, where $b_1$ is an arbitrary element of $H_{i\lambda }$. Let $F_{i\lambda }(a)=0$. Then equation (21) reduces to the equation

$${(D-\lambda I)}^{m-1}x=R_{\lambda }(a)+b_1.$$

(22)

Put $z={(D-\lambda I)}^{m-2}x$. Then this equation has the form

$$(D-\lambda I)z=R_{\lambda }(a)+b_1.$$

(23)

By Theorem 5, this equation is solvable if and only if $F_{i\lambda }(R_{\lambda }(a)+b_1)=F_{i\lambda }(R_{\lambda }(a))+F_{i\lambda }(b_1)=F_{i\lambda }(a)+F_{i\lambda }(b_1)=F_{i\lambda }(b_1)=0$. Therefore a general solution of equation (23) has the form $z=R_{\lambda }^2(a)+b_2$, where $b_2$ is an arbitrary element of $H_{i\lambda }$. By induction, we obtain that a general solution of equation (21) has the form $x=R_{\lambda }^m(a)+b$, where b is an arbitrary element of $H_{i\lambda }$. The lemma is proved. □

By this lemma, a solution of equation (20) reduces to a solution of the equation

$${(D-{\lambda }_{2}I)}^{m_2}\cdots {(D-{\lambda }_{k}I)}^{m_k}x=R_{{\lambda }_1}^{m_1}{R}_{{\lambda }_{r+1}}\cdots R_{{\lambda }_n}a+b_1,$$

(24)

where $b_1$ is an arbitrary element of $H_{i{\lambda }_1}$. Using Lemma 3, by induction we obtain that a general solution of equation (20) has the form (16).  □

6 Periodic solutions of the system of linear differential equations with constant coefficients

Let $(a_1,\dots ,a_n)$ be a vector-line, where $a_i\in H$, $i=1,\dots ,n$. Denote by ⊤ the operator of transposition of a matrix. The ${(a_1,\dots ,a_n)}^{\mathrm{\top }}$ denotes a vector-column of $a_i\in H$, $i=1,\dots ,n$. Denote by $H^{\mathrm{\top }n}$ the set of all vectors ${(a_1,\dots ,a_n)}^{\mathrm{\top }}$, where $a_i\in H$, $i=1,\dots ,n$. For $a={(a_1,\dots ,a_n)}^{\mathrm{\top }}\in H^{\mathrm{\top }n}$ put $Da={(D{a}_1,\dots ,D{a}_n)}^{\mathrm{\top }}$.

We consider the following system of linear differential equations:

$$Dx=Ax+a,$$

(25)

where $a\in H^{\mathrm{\top }n}$, $x={(x_1,\dots ,x_n)}^{\mathrm{\top }}$ and A is a complex $n\times n$ matrix.

Definition 7 Systems $Dx=Ax+a$ and $Dy=By+b$, where A, B are complex $n\times n$-matrices, $a,b\in H^{\mathrm{\top }n}$ are called equivalent, if there exists a complex $n\times n$-matrix K such that $detK\ne 0$, $A=K^{-1}BK$ and $a=K^{-1}b$.

In this case $y=Kx$.

Proposition 5 Every system (25) is equivalent to the system of the form $Dy=By+b$, where the matrix B has the Jordan form.

Proof For A there exists a complex $n\times n$-matrix K such that $A=K^{-1}BK$, where B is the Jordan normal form of A. From $Dx=Ax+a$, we obtain $Dy=By+b$, where $y=Kx$ and $b=Ka$. □

By this proposition, a solution of system (25) reduces to a solution of the system of the form (25), where B has the Jordan normal form. Let B have the form

$$\left(\begin{array}{cccc}{B}_1& 0& \dots & 0\\ 0& B_2& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& ⋮& B_m\end{array}\right),$$

(26)

where $B_j$ is a Jordan block of the $n_j$th order, $n_1+\cdots +n_m=n$. Then a solution of system (25), where B has the form (26), reduces to a solution of the following system of equations:

$$\{\begin{array}{c}D{u}_1=B_1{u}_1+b_1;\hfill \\ D{u}_2=B_2{u}_2+b_2;\hfill \\ ⋮\hfill \\ D{u}_m=B_m{u}_m+b_m,\hfill \end{array}$$

(27)

where $B_j$ is a Jordan block of the $n_j$th order, $b_j\in H^{\mathrm{\top }{n}_j}$, $u_j\in H^{\mathrm{\top }{n}_j}$ and $x={(u_1,u_2,\dots ,u_m)}^{\mathrm{\top }}$. Therefore a solution of system (27) reduces to a solution of the equation of the form

$$Dx=Gx+b,$$

(28)

where B is a Jordan block of the q th order with eigenvalue λ: $g_i^i=\lambda$, $i=1,\dots ,q$; $g_{i+1}^i=1$, $i=1,\dots ,q-1$; $g_j^i=0$, $j-i<0$ and $j-i>1$.

Theorem 8 Let $Dx=Gx+b$ be a system of the form (28), where G is a Jordan block of the qth order with eigenvalue λ and $b={(b_1,\dots ,b_q)}^{\mathrm{\top }}\in H^{\mathrm{\top }q}$. Then

• (i) for the case $\lambda \in C\setminus Spec(H)$, the system has the unique solution $x={(x_1,\dots ,x_q)}^{\mathrm{\top }}\in H^{\mathrm{\top }q}$, where:

  

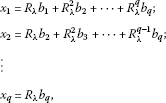
• (ii) for the case $\lambda \in Spec(H)$, $\lambda =ip$, $p\in Z$, the system has a solution if and only if $F_p{b}_q=0$,

• (iii) for the case $\lambda \in Spec(H)$, $\lambda =ip$, $p\in Z$ and $F_p{b}_q=0$, a general solution $x={(x_1,\dots ,x_q)}^{\mathrm{\top }}\in H^{\mathrm{\top }q}$ of the system has the form

  $$\{\begin{array}{c}{x}_1={\sum }_{k=1}^{q-1}{R}_{ip}^k(b_k-F_p{b}_k)+R_{ip}^q(b_q)+c;\hfill \\ x_{q-r}={\sum }_{k=1}^r{R}_{ip}^k(b_{q-r-1+k}-F_p{b}_{q-r-1+k})+R_{ip}^{r+1}(b_q-F_p{b}_{q-r-1}),\hfill \\ r=1,\dots ,q-2;\hfill \\ x_q=R_{ip}{b}_q-F_p{b}_{q-1},\hfill \end{array}$$

  (29)

where c is an arbitrary element of $H_p$.

Proof System (28) has the form

$$\{\begin{array}{c}D{x}_1-\lambda x_1=x_2+b_1;\hfill \\ D{x}_2-\lambda x_2=x_3+b_2;\hfill \\ ⋮\hfill \\ D{x}_{q-1}-\lambda x_{q-1}=x_q+b_{q-1};\hfill \\ D{x}_q-\lambda x_q=b_q.\hfill \end{array}$$

(30)

Let $\lambda \in C\setminus Spec(H)$. From (30), using the operator $R_{\lambda }$, we obtain

$$x_q=R_{\lambda }{b}_q,x_{q-1}=R_{\lambda }{b}_{q-1}+R_{\lambda }^2{b}_q,\dots ,x_1=\sum _{k=1}^q{R}_{\lambda }^k{b}_k.$$

Let $\lambda \in Spec(H)$. Then $\lambda =ip$ for some $p\in Z$. By Theorem 5, the equation

$$D{x}_q-ip{x}_q=b_q,$$

(31)

is solvable if and only if $F_p{b}_q=0$.

Let $F_p{b}_q=0$. By Theorem 5, a general solution of (31) has the form $x_q=R_{ip}{b}_q+c_q$, where $c_q$ is an arbitrary element of $H_{ip}$. In this case, the equation $D{x}_{q-1}-ip{x}_{q-1}=x_q+b_{q-1}$ has the form

$$D{x}_{q-1}-ip{x}_{q-1}=R_{ip}{b}_q+c_q+b_{q-1}.$$

(32)

By Theorem 5, this equation has a solution if and only if

$$F_{ip}(R_{ip}{b}_q+c_q+b_{q-1})=0.$$

(33)

By $F_{ip}(b_q)=0$ and Theorem 3(ii), (iii), we have $F_{ip}{R}_{ip}{b}_q=R_{ip}{F}_{ip}{b}_q=0$. Hence (33) is equivalent to $F_{ip}(c_q+b_{q-1})=0$. Then $F_{ip}{c}_q=-F_{ip{b}_{q-1}}$. By $c_q\in H_{ip}$, we obtain $c_q=F_{ip}{c}_q=-F_{ip}{b}_{q-1}$. Thus equation (33) is solvable if and only if $c_q=-F_{ip}{b}_{q-1}$. Then equation (32) has the form $D{x}_{q-1}-ip{x}_{q-1}=(b_{q-1}-F_{ip}{b}_{q-1})+R_{ip}{b}_q$. By Theorem 5, a general solution of this equation is $x_{q-1}=R_{ip}(b_{q-1}-F_{ip}{b}_{q-1})+R_{ip}^2{b}_q+c_{q-1}$, where $c_{q-1}$ is an arbitrary element of $H_{ip}$. Then the equation $D{x}_{q-2}-ip{x}_{q-2}=x_{q-1}+b_{q-2}$ has the form $D{x}_{q-2}-ip{x}_{q-2}=(b_{q-2}+c_{q-1})+R_{ip}(b_{q-1}-F_{ip}{b}_{q-1})+R_{ip}^2{b}_q$. As above, this equation is solvable if and only if $c_{q-1}=-F_{ip}{b}_{q-2}$. Similarly, by induction, we obtain a solution of system (30) in the form (29). □