- Research
- Open access
- Published:
On a relation between Schur, Hardy-Littlewood-Pólya and Karamata’s theorem and an inequality of some products of derived from the Furuta inequality
Journal of Inequalities and Applications volume 2013, Article number: 137 (2013)
Abstract
We show a functional inequality of some products of as an application of an operator inequality. Furthermore, we will show it can be deduced from a classical theorem on majorization and convex functions.
MSC:26D07, 26A09, 26A51, 39B62, 47A63.
1 Introduction
It is easy to see the inequalities
or
for arbitrary if they are provided as the matter to be proved. However, if we would like to estimate functions of the form
by simpler ones, how can we guess what forms and coefficients are possible?
Example The following inequality does not hold on an interval contained in .
In Section 2, we prove a certain functional inequality as mentioned above, although the efficiency and possible applications to other branches of mathematics are still to be clarified.
In Section 3, we show that the functional inequality derived in Section 2 can be easily deduced from Schur, Hardy-Littlewood-Pólya and Karamata’s theorem on majorization and convex functions. Although the proof presented in Section 2 looks like a detour, one should note that it naturally arises as a byproduct of the Furuta inequality, which is an epochmaking extension of the celebrated Löwner-Heinz inequality [1, 2]. It seems worthy to compare various ways to derive fundamental functional inequalities, for it might contribute to clarify relations between their background theories and to suggest further developments.
2 An inequality of some products of
The proof of the following theorem is based on an operator inequality by Furuta [3] and an argument related to the best possibility of that by Tanahashi [4]. The main feature of the argument is applying an order-preserving operator inequality to matrices which contain variables as their entries. It might be a new method to obtain functional inequalities systematically.
Theorem 2.1 [5]
Let , and with . If , then
Proposition 2.2 Let , . Then, for arbitrary ,
Proof Put . Since , we have , and hence Proposition 2.2 immediately follows from Theorem 2.1. □
Theorem 2.3 Let , , and . Then, for arbitrary ,
Proof For a moment, we add and to the assumption. Apply Proposition 2.2 with , , then the inequality (1) implies
In general, note that . Dividing by , we have
By the first part of the proof,
for arbitrary . By substituting to x in the above inequality, it is immediate to see the inequality (2). □
Definition 2.4 For a finite sequence of real numbers, we denote its decreasing rearrangement by .
For two vectors and , p is said to be majorized by q and denoted by if the following inequalities are satisfied:

Theorem 2.5 Let n be a natural number. Suppose , and . Then, for arbitrary ,
If n is even, the inequality (3) holds for arbitrary . If n is odd, the reverse inequality of (3) holds for arbitrary .
Proof The case is exactly Theorem 2.3. Suppose that the case n is valid. We may assume , and
There exists a number k such that and
Take a real number which is determined by . Then
By the case ,
Since
we have
and
Note that

by the assumption of the induction.
If , then the n-tuples and satisfy the assumption of the case n, so we may assume by using the inequality (4).
Equality (5) and yield
If , then the n-tuples and satisfy the assumption of the case n, so we may assume . For , we have
and hence
Similarly, we have

Therefore, n-tuples , satisfy the assumption of the case n, and so we can obtain
for arbitrary .
From (4) and (6), it is immediate to see that
for .
The last assertion of the theorem can be easily seen by substituting for and multiplying to both sides.
This completes the proof. □
Remark 2.6 Each following example of the case does not satisfy one of the conditions for parameters in the assumption of Theorem 2.5, and the inequality does not hold for all .
-
(i)
-
(ii)
-
(iii)
-
(iv)
Remark 2.7 There exists an example of the case such that , but the inequality holds for .
Indeed,

3 A proof by Schur, Hardy-Littlewood-Pólya and Karamata’s theorem
Theorem 2.5 is a special case of a more general theorem on majorization and convex functions.
Theorem 3.1 (C.1. Proposition in [6], Theorem 108 in [7], Karamata [8])
Let n be a natural number and , be real numbers from an interval . If , then
for every real-valued convex function f on .
Proposition 3.2 Let be a fixed real number. Then
is convex on the interval .
Although it is definitely elementary to prove this proposition, we will give it for the sake of completeness.
Proof One can calculate the derivatives of f with respect to t,

The signature of is the same as g, where
It is easy to see
The signature of is the same as , where
It is also easy to see
The signature of is the same as , where
Now we have
Therefore, is increasing on and so that (), and hence ().
Again, therefore, is increasing on and so that (), and hence ().
Once again, therefore, g is increasing on and so that (), and hence (), namely, f is convex on the interval . This completes the proof of Proposition 3.2. □
The completion of the proof of Theorem 2.5 by using Schur, Hardy-Littlewood-Pólya and Karamata’s theorem.
For arbitrary , is a convex function on the interval , so we can apply Theorem 3.1 to obtain
and hence we have
The rest is identical to the proof of Theorem 2.5. This completes the proof.
References
Löwner K: Über monotone Matrixfunktionen. Math. Z. 1934, 38: 177–216. 10.1007/BF01170633
Heinz E: Beiträge zur Störungstheorie der Spektralzerlegung. Math. Ann. 1951, 123: 415–438. 10.1007/BF02054965
Furuta T:
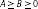 assures
assures 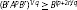 for
for  ,
,  ,
, 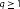 with
with 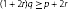 . Proc. Am. Math. Soc. 1987, 101(1):85–88.
. Proc. Am. Math. Soc. 1987, 101(1):85–88.Tanahashi K: Best possibility of the Furuta inequality. Proc. Am. Math. Soc. 1996, 124: 141–146. 10.1090/S0002-9939-96-03055-9
Watanabe K: An application of matrix inequalities to certain functional inequalities involving fractional powers. J. Inequal. Appl. 2012., 2012: Article ID 221. doi:10.1186/1029–242X-2012–221
Marshall AW, Olkin I, Arnold BC: Inequalities: Theory of Majorization and Its Applications. 2nd edition. Springer, Berlin; 2011.
Hardy GH, Littlewood JE, Pólya G: Inequalities. 2nd edition. Cambridge University Press, Cambridge; 1952.
Karamata J: Sur une inegalite relative aux fonctions convexes. Publ. Math. Univ. (Belgr.) 1932, 1: 145–148.
Acknowledgements
The author is grateful to the referee, for the careful reading of the paper and for the helpful suggestions and comments. The author was supported in part by Grants-in-Aid for Scientific Research, Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that he has no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Watanabe, K. On a relation between Schur, Hardy-Littlewood-Pólya and Karamata’s theorem and an inequality of some products of derived from the Furuta inequality. J Inequal Appl 2013, 137 (2013). https://doi.org/10.1186/1029-242X-2013-137
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-137
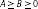 assures
assures 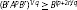 for
for  ,
,  ,
, 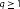 with
with 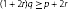 . Proc. Am. Math. Soc. 1987, 101(1):85–88.
. Proc. Am. Math. Soc. 1987, 101(1):85–88.