Strong convergence theorems for modifying Halpern iterations for a totally quasi-ϕ-asymptotically nonexpansive multi-valued mapping in reflexive Banach spaces

Abstract

In this paper, we discuss an iterative sequence for a totally quasi-ϕ-asymptotically nonexpansive multi-valued mapping for modifying Halpern’s iterations and establish some strong convergence theorems under certain conditions. We utilize the theorems to study a modified Halpern iterative algorithm for a system of equilibrium problems. The results improve and extend the corresponding results of Chang et al. (Appl. Math. Comput. 218:6489-6497, 2012).

MSC:47J05, 47H09, 49J25.

1 Introduction

Throughout this paper, we denote by N and R the sets of positive integers and real numbers, respectively. Let D be a nonempty closed subset of a real Banach space X. A mapping $T:D\to D$ is said to be nonexpansive if $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$ for all $x,y\in D$. Let $N(D)$ and $CB(D)$ denote the family of nonempty subsets and nonempty bounded closed subsets of D, respectively. The Hausdorff metric on $CB(D)$ is defined by

$$H(A_1,A_2)=max\{\underset{x\in A_1}{sup}d(x,A_2),\underset{y\in A_2}{sup}d(y,A_1)\}$$

for $A_1,A_2\in CB(D)$, where $d(x,A_2)=inf\{\parallel x-y\parallel ,y\in A_2\}$. The multi-valued mapping $T:D\to CB(D)$ is called nonexpansive if $H(Tx,Ty)\le \parallel x-y\parallel$ for all $x,y\in D$. An element $p\in D$ is called a fixed point of $T:D\to CB(D)$ if $p\in T(p)$. The set of fixed points of T is represented by $F(T)$.

In the sequel, denote $S(X)=\{x\in X:\parallel x\parallel =1\}$. A Banach space X is said to be strictly convex if $\parallel \frac{x+y}{2}\parallel \le 1$ for all $x,y\in S(X)$ and $x\ne y$. A Banach space is said to be uniformly convex if ${lim}_{n\to \mathrm{\infty }}\parallel x_n-y_n\parallel =0$ for any two sequences $\{x_n\},\{y_n\}\subset S(X)$ and ${lim}_{n\to \mathrm{\infty }}\parallel \frac{x_n+y_n}{2}\parallel =0$. The norm of the Banach space X is said to be Gâteaux differentiable if for each $x,y\in S(X)$, the limit

$$\underset{t\to 0}{lim}\frac{\parallel x+ty\parallel -\parallel x\parallel }{t}$$

(1.1)

exists. In this case, X is said to be smooth. The norm of the Banach space X is said to be Fréchet differentiable if for each $x\in S(X)$, the limit (1.1) is attained uniformly for $y\in S(x)$, and the norm is uniformly Fréchet differentiable if the limit (1.1) is attained uniformly for $x,y\in S(X)$. In this case, X is said to be uniformly smooth.

Let X be a real Banach space with dual $X^{\ast }$. We denote by J the normalized duality mapping from X to $2^{X^{\ast }}$ which is defined by

$$J(x)=\{x^{\ast }\in X^{\ast }:〈x,x^{\ast }〉={\parallel x\parallel }^2={\parallel x^{\ast }\parallel }^2\},x\in X,$$

where $〈\cdot ,\cdot 〉$ denotes the generalized duality pairing.

Remark 1.1 The following basic properties for the Banach space X and for the normalized duality mapping J can be found in Cioranescu [1].

• (1) X ($X^{\ast }$, resp.) is uniformly convex if and only if $X^{\ast }$ (X, resp.) is uniformly smooth.

• (2) If X is smooth, then J is single-valued and norm-to-weak^∗ continuous.

• (3) If X is reflexive, then J is onto.

• (4) If X is strictly convex, then $Jx\cap Jy\ne \mathrm{\Phi }$ for all $x,y\in X$.

• (5) If X has a Fréchet differentiable norm, then J is norm-to-norm continuous.

• (6) If X is uniformly smooth, then J is uniformly norm-to-norm continuous on each bounded subset of X.

• (7) Each uniformly convex Banach space X has the Kadec-Klee property, i.e., for any sequence $\{x_n\}\subset X$, if $x_n\rightharpoonup x\in X$ and $\parallel x_n\parallel \to \parallel x\parallel$, then $x_n\to x\in X$.

Next we assume that X is a smooth, strictly convex, and reflexive Banach space and D is a nonempty closed convex subset of X. In the sequel, we always use $\varphi :X\times X\to R^{+}$ to denote the Lyapunov bifunction defined by

$$\varphi (x,y)={\parallel x\parallel }^2-2〈x,Jy〉+{\parallel y\parallel }^2,x,y\in X.$$

(1.2)

It is obvious from the definition of the function ϕ that

(1.3)

(1.4)

and

$$\varphi (x,J^{-1}(\alpha Jy+(1-\alpha )Jz))\le \alpha \varphi (x,y)+(1-\alpha )\varphi (x,z)$$

(1.5)

for all $\alpha \in [0,1]$ and $x,y,z\in X$.

Following Alber [2], the generalized projection ${\mathrm{\Pi }}_D:X\to D$ is defined by

$${\mathrm{\Pi }}_D(x)=arg\underset{y\in D}{inf}\varphi (y,x),\mathrm{\forall }x\in X.$$

Many problems in nonlinear analysis can be reformulated as a problem of finding a fixed point of a nonexpansive mapping.

Remark 1.2 (see [3])

Let ${\mathrm{\Pi }}_D$ be the generalized projection from a smooth, reflexive and strictly convex Banach space X onto a nonempty closed convex subset D of X, then ${\mathrm{\Pi }}_D$ is a closed and quasi-ϕ-nonexpansive from X onto D.

In 1953, Mann [4] introduced the following iterative sequence $\{x_n\}$:

$$x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,$$

where the initial guess $x_1\in D$ is arbitrary and $\{{\alpha }_n\}$ is a real sequence in $[0,1]$. It is known that under appropriate settings the sequence $\{x_n\}$ converges weakly to a fixed point of T. However, even in a Hilbert space, the Mann iteration may fail to converge strongly [5]. Some attempts to construct an iteration method guaranteeing the strong convergence have been made. For example, Halpern [6] proposed the following so-called Halpern iteration:

$$x_{n+1}={\alpha }_{n}u+(1-{\alpha }_n)T{x}_n,$$

where $u,x_1\in D$ are arbitrarily given and $\{{\alpha }_n\}$ is a real sequence in $[0,1]$. Another approach was proposed by Nakajo and Takahashi [7]. They generated a sequence as follows:

$$\{\begin{array}{c}{x}_1\in X\text{is arbitrary};\hfill \\ y_n={\alpha }_{n}u+(1-{\alpha }_n)T{x}_n,\hfill \\ C_n=\{z\in D:\parallel y_n-z\parallel \le \parallel x_n-z\parallel \},\hfill \\ Q_n=\{z\in D:〈x_n-z,x_1-x_n〉\ge 0\},\hfill \\ x_{n+1}=P_{C_n\cap Q_n}{x}_1(n=1,2,\dots ),\hfill \end{array}$$

(1.6)

where $\{{\alpha }_n\}$ is a real sequence in $[0,1]$ and $P_K$ denotes the metric projection from a Hilbert space H onto a closed convex subset K of H. It should be noted here that the iteration above works only in the Hilbert space setting. To extend this iteration to a Banach space, the concept of relatively nonexpansive mappings and quasi-ϕ-nonexpansive mappings have been introduced by Aoyama et al. [8], Chang et al. [9, 10], Chidume et al. [11], Matsushita et al. [12–14], Qin et al. [15], Song et al. [16], Wang et al. [17] and others.

Inspired by the work of Matsushita and Takahashi, in this paper, we introduce modifying Halpern-Mann iterations sequence for finding a fixed point of a multi-valued mapping $T:D\to CB(D)$ and prove some strong convergence theorems. The results presented in the paper improve and extend the corresponding results in [9].

2 Preliminaries

In the sequel, we denote the strong convergence and weak convergence of the sequence $\{x_n\}$ by $x_n\to x$ and $x_n\rightharpoonup x$, respectively.

Lemma 2.1 (see [2])

Let X be a smooth, strictly convex and reflexive Banach space, and let D be a nonempty closed convex subset of X. Then the following conclusions hold:

• (a)
  $$\varphi (x,y)=0$$

  if and only if $x=y$.

• (b)
  $$\varphi (x,{\mathrm{\Pi }}_{D}y)+\varphi ({\mathrm{\Pi }}_{D}y,y)\le \varphi (x,y)$$

  , $\mathrm{\forall }x,y\in D$.

• (c) If $x\in X$ and $z\in D$, then $z={\mathrm{\Pi }}_{D}x$ if and only if $〈z-y,Jx-Jz〉\ge 0$, $\mathrm{\forall }y\in D$.

Lemma 2.2 (see [9])

Let X be a real uniformly smooth and strictly convex Banach space with the Kadec-Klee property, and let D be a nonempty closed convex subset of X. Let $\{x_n\}$ and $\{y_n\}$ be two sequences in D such that $x_n\to p$ and $\varphi (x_n,y_n)\to 0$, where ϕ is the function defined by (1.2), then $y_n\to p$.

Definition 2.1 A point $p\in D$ is said to be an asymptotic fixed point of a multi-valued mapping $T:D\to CB(D)$ if there exists a sequence $\{x_n\}\subset D$ such that $x_n\rightharpoonup x\in X$ and $d(x_n,T(x_n))\to 0$. Denote the set of all asymptotic fixed points of T by $\hat{F}(T)$.

Definition 2.2

• (1) A multi-valued mapping $T:D\to CB(D)$ is said to be relatively nonexpansive if $F(T)\ne \mathrm{\Phi }$, $\hat{F}(T)=F(T)$ and $\varphi (p,z)\le \varphi (p,x)$, $\mathrm{\forall }x\in D$, $p\in F(T)$, $z\in T(x)$.

• (2) A multi-valued mapping $T:D\to CB(D)$ is said to be closed if for any sequence $\{x_n\}\subset D$ with $x_n\to x\in X$ and $d(y,T(x_n))\to 0$, then $d(y,T(x))=0$.

Remark 2.1 If H is a real Hilbert space, then $\varphi (x,y)={\parallel x-y\parallel }^2$ and ${\mathrm{\Pi }}_D$ is the metric projection $P_D$ of H onto D.

Next, we present an example of a relatively nonexpansive multi-valued mapping.

Example 2.1 (see [18])

Let X be a smooth, strictly convex and reflexive Banach space, let D be a nonempty closed and convex subset of X, and let $f:D\times D\to R$ be a bifunction satisfying the conditions: (A1) $f(x,x)=0$, $\mathrm{\forall }x\in D$; (A2) $f(x,y)+f(y,x)\le 0$, $\mathrm{\forall }x,y\in D$; (A3) for each $x,y,z\in D$, ${lim}_{t\to 0}f(tz+(1-t)x,y)\le f(x,y)$; (A4) for each given $x\in D$, the function $y\mapsto f(x,y)$ is convex and lower semicontinuous. The so-called equilibrium problem for f is to find an $x^{\ast }\in D$ such that $f(x^{\ast },y)\ge 0$, $\mathrm{\forall }y\in D$. The set of its solutions is denoted by $EP(f)$.

Let $r>0$, $x\in D$ and define a multi-valued mapping $T_r:D\to N(D)$ as follows:

$$T_r(x)=\{z\in D,f(z,y)+\frac{1}{r}〈y-z,Jz-Jx〉\ge 0,\mathrm{\forall }y\in D\},\mathrm{\forall }x\in D,$$

(2.1)

then (1) $T_r$ is single-valued, and so $\{z\}=T_r(x)$; (2) $T_r$ is a relatively nonexpansive mapping, therefore, it is a closed quasi-ϕ-nonexpansive mapping; (3) $F(T_r)=EP(f)$.

Definition 2.3

• (1) A multi-valued mapping $T:D\to CB(D)$ is said to be quasi-ϕ-nonexpansive if $F(T)\ne \mathrm{\Phi }$ and $\varphi (p,z)\le \varphi (p,x)$, $\mathrm{\forall }x\in D$, $p\in F(T)$, $z\in Tx$.

• (2) A multi-valued mapping $T:D\to CB(D)$ is said to be quasi-ϕ-asymptotically nonexpansive if $F(T)\ne \mathrm{\Phi }$ and there exists a real sequence $k_n\subset [1,+\mathrm{\infty })$, $k_n\to 1$, such that

  $$\varphi (p,z_n)\le k_n\varphi (p,x),\mathrm{\forall }x\in D,p\in F(T),z_n\in T^{n}x.$$

  (2.2)

• (3) A multi-valued mapping $T:D\to CB(D)$ is said to be totally quasi-ϕ-asymptotically nonexpansive if $F(T)\ne \mathrm{\Phi }$ and there exist nonnegative real sequences $\{v_n\}$, $\{{\mu }_n\}$ with $v_n,{\mu }_n\to 0$ (as $n\to \mathrm{\infty }$) and a strictly increasing continuous function $\zeta :R^{+}\to R^{+}$ with $\zeta (0)=0$ such that

  

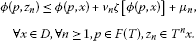  (2.3)

Remark 2.2 From the definitions, it is obvious that a relatively nonexpansive multi-valued mapping is a quasi-ϕ-nonexpansive multi-valued mapping, and a quasi-ϕ-nonexpansive multi-valued mapping is a quasi-ϕ-asymptotically nonexpansive multi-valued mapping, and a quasi-ϕ-asymptotically nonexpansive multi-valued mapping is a total quasi-ϕ-asymptotically nonexpansive multi-valued mapping, but the converse is not true.

Lemma 2.3 Let X and D be as in Lemma 2.2. Let $T:D\to CB(D)$ be a closed and totally quasi-ϕ-asymptotically nonexpansive multi-valued mapping with nonnegative real sequences $\{v_n\}$, $\{{\mu }_n\}$ and a strictly increasing continuous function $\zeta :R^{+}\to R^{+}$ with $\zeta (0)=0$. If $v_n,{\mu }_n\to 0$ (as $n\to \mathrm{\infty }$) and ${\mu }_1=0$, then $F(T)$ is a closed and convex subset of D.

Proof Let $\{x_n\}$ be a sequence in $F(T)$ such that $x_n\to x^{\ast }$. Since T is a totally quasi-ϕ-asymptotically nonexpansive multi-valued mapping, we have

$$\varphi (x_n,z)\le \varphi (x_n,x^{\ast })+v_1\zeta \left[\varphi (x_n,x^{\ast })\right]$$

for all $z\in T{x}^{\ast }$ and for all $n\in N$. Therefore,

$$\varphi (x^{\ast },z)=\underset{n\to \mathrm{\infty }}{lim}\varphi (x_n,z)\le \underset{n\to \mathrm{\infty }}{lim}\{\varphi (x_n,x^{\ast })+v_1\zeta \left[\varphi (x_n,x^{\ast })\right]\}=\varphi (x^{\ast },x^{\ast })=0.$$

By Lemma 2.1(a), we obtain $z=x^{\ast }$. Hence, $T{x}^{\ast }=\{x^{\ast }\}$. So, we have $x^{\ast }\in F(T)$. This implies $F(T)$ is closed.

Let $p,q\in F(T)$ and $t\in (0,1)$, and put $w=tp+(1-t)q$. Next we prove that $w\in F(T)$. Indeed, in view of the definition of ϕ, letting $z_n\in T^{n}w$, we have

$$\begin{array}{rcl}\varphi (w,z_n)& =& {\parallel w\parallel }^2-2〈w,J{z}_n〉+{\parallel z_n\parallel }^2\\ =& {\parallel w\parallel }^2-2〈tp+(1-t)q,J{z}_n〉+{\parallel z_n\parallel }^2\\ =& {\parallel w\parallel }^2+t\varphi (p,z_n)+(1-t)\varphi (q,z_n)-t{\parallel p\parallel }^2-(1-t){\parallel q\parallel }^2.\end{array}$$

(2.4)

Since

(2.5)

Substituting (2.4) into (2.5) and simplifying it, we have

$$\varphi (w,z_n)\le t{v}_n\zeta [\varphi (p,w)]+(1-t)v_n\zeta [\varphi (q,w)]+{\mu }_n\to 0(\text{as }n\to \mathrm{\infty }).$$

By Lemma 2.2, we have $z_n\to w$. This implies that $z_{n+1}(\in T{T}^{n}w)\to w$. Since T is closed, we have $Tw=\{w\}$, i.e., $w\in F(T)$. This completes the proof of Lemma 2.3. □

Definition 2.4 A mapping $T:D\to CB(D)$ is said to be uniformly L-Lipschitz continuous if there exists a constant $L>0$ such that $\parallel x_n-y_n\parallel \le L\parallel x-y\parallel$, where $x,y\in D$, $x_n\in T^{n}x$, $y_n\in T^{n}y$.

3 Main results

Theorem 3.1 Let X be a real uniformly smooth and strictly convex Banach space with the Kadec-Klee property, let D be a nonempty closed convex subset of X, and let $T:D\to CB(D)$ be a closed and uniformly L-Lipschitz continuous totally quasi-ϕ-asymptotically nonexpansive multi-valued mapping with nonnegative real sequences $\{v_n\}$, $\{{\mu }_n\}$, $v_n,{\mu }_n\to 0$ (as $n\to \mathrm{\infty }$) and a strictly increasing continuous function $\zeta :R^{+}\to R^{+}$ with $\zeta (0)=0$ satisfying condition (2.3). Let $\{{\alpha }_n\}$ be a sequence in $[0,1]$ such that ${\alpha }_n\to 0$. If $\{x_n\}$ is the sequence generated by

$$\{\begin{array}{c}{x}_1\in X\mathit{\text{is arbitrary}};D_1=D,\hfill \\ y_n=J^{-1}[{\alpha }_{n}J{x}_1+(1-{\alpha }_n)J{z}_n],z_n\in T^n{x}_n,\hfill \\ D_{n+1}=\{z\in D_n:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)+{\xi }_n\},\hfill \\ x_{n+1}={\mathrm{\Pi }}_{D_{n+1}}{x}_1(n=1,2,\dots ),\hfill \end{array}$$

(3.1)

where ${\xi }_n=v_n{sup}_{p\in F(T)}\zeta [\varphi (p,x_n)]+{\mu }_n$, $F(T)$ is the fixed point set of T, and ${\mathrm{\Pi }}_{D_{n+1}}$ is the generalized projection of X onto $D_{n+1}$. If $F(T)$ is nonempty and ${\mu }_1=0$, then ${lim}_{n\to \mathrm{\infty }}{x}_n={\mathrm{\Pi }}_{F(T)}{x}_1$.

Proof (I) First, we prove that $D_n$ is a closed and convex subset in D.

By the assumption, $D_1=D$ is closed and convex. Suppose that $D_n$ is closed and convex for some $n\ge 1$. In view of the definition of ϕ, we have

$$\begin{array}{rcl}{D}_{n+1}& =& \{z\in D_n:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)+{\xi }_n\}\\ =& \{z\in D:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)+{\xi }_n\}\cap D_n\\ =& \{z\in D:2{\alpha }_n〈z,J{x}_1〉+2(1-{\alpha }_n)〈z,J{x}_n〉-2〈z,J{y}_n〉\\ \le {\alpha }_n{\parallel x_1\parallel }^2+(1-{\alpha }_n){\parallel x_n\parallel }^2-{\parallel y_n\parallel }^2\}\cap D_n.\end{array}$$

This shows that $D_{n+1}$ is closed and convex. The conclusions are proved.

• (II) Next, we prove that $F(T)\subset D_n$ for all $n\ge 1$.

In fact, it is obvious that $F(T)\subset D_1$. Suppose that $F(T)\subset D_n$. Hence, for any $u\in F(T)\subset D_n$, by (1.5), we have

$$\begin{array}{rcl}\varphi (u,y_n)& =& \varphi (u,J^{-1}({\alpha }_{n}J{x}_1+(1-{\alpha }_n)J{z}_n))\\ \le & {\alpha }_n\varphi (u,x_1)+(1-{\alpha }_n)\varphi (u,z_n)\\ \le & {\alpha }_n\varphi (u,x_1)+(1-{\alpha }_n)\{\varphi (u,x_n)+v_n\zeta [\varphi (u,x_n)]+{\mu }_n\}\\ \le & {\alpha }_n\varphi (u,x_1)+(1-{\alpha }_n)\{\varphi (u,x_n)+v_n\underset{p\in F(T)}{sup}\zeta [\varphi (p,x_n)]+{\mu }_n\}\\ =& {\alpha }_n\varphi (u,x_1)+(1-{\alpha }_n)\varphi (u,x_n)+{\xi }_n.\end{array}$$

(3.2)

This shows that $u\in F(T)\subset D_{n+1}$, and so $F(T)\subset D_n$.

• (III) Now we prove that $\{x_n\}$ converges strongly to some point $p^{\ast }$.

In fact, since $x_n={\mathrm{\Pi }}_{D_n}{x}_1$, from Lemma 2.1(c), we have

$$〈x_n-y,J{x}_1-J{x}_n〉\ge 0,\mathrm{\forall }y\in D_n.$$

Again since $F(T)\subset D_n$, we have

$$〈x_n-u,J{x}_1-J{x}_n〉\ge 0,\mathrm{\forall }u\in F(T).$$

It follows from Lemma 2.1(b) that for each $u\in F(T)$ and for each $n\ge 1$,

$$\varphi (x_n,x_1)=\varphi ({\mathrm{\Pi }}_{D_n}{x}_1,x_1)\le \varphi (u,x_1)-\varphi (u,x_n)\le \varphi (u,x_1).$$

(3.3)

Therefore, $\{\varphi (x_n,x_1)\}$ is bounded and so is $\{x_n\}$. Since $x_n={\mathrm{\Pi }}_{D_n}{x}_1$ and $x_{n+1}={\mathrm{\Pi }}_{D_{n+1}}{x}_1\in D_{n+1}\subset D_n$, we have $\varphi (x_n,x_1)\le \varphi (x_{n+1},x_1)$. This implies that $\{\varphi (x_n,x_1)\}$ is nondecreasing. Hence ${lim}_{n\to \mathrm{\infty }}\varphi (x_n,x_1)$ exists. Since X is reflexive, there exists a subsequence $\{x_{n_i}\}\subset \{x_n\}$ such that $x_{n_i}\rightharpoonup p^{\ast }$ (some point in $D=D_1$). Since $D_n$ is closed and convex and $D_{n+1}\subset D_n$. This implies that $D_n$ is weakly closed and $p^{\ast }\in D_n$ for each $n\ge 1$. In view of $x_{n_i}={\mathrm{\Pi }}_{D_{n_i}}{x}_1$, we have

$$\varphi (x_{n_i},x_1)\le \varphi (p^{\ast },x_1),\mathrm{\forall }{n}_i\ge 1.$$

Since the norm $\parallel \cdot \parallel$ is weakly lower semi-continuous, we have

$$\begin{array}{rcl}\underset{n_i\to \mathrm{\infty }}{lim}inf\varphi (x_n,x_1)& =& \underset{n_i\to \mathrm{\infty }}{lim}inf({\parallel x_{n_i}\parallel }^2-2〈x_{n_i},J{x}_1〉+{\parallel x_1\parallel }^2)\\ \ge & {\parallel p^{\ast }\parallel }^2-2〈p^{\ast },J{x}_1〉+{\parallel x_1\parallel }^2\\ =& \varphi (p^{\ast },x_1),\end{array}$$

and so

$$\begin{array}{rcl}\varphi (p^{\ast },x_1)& \le & \underset{n_i\to \mathrm{\infty }}{lim}inf\varphi (x_n,x_1)\\ \le & \underset{n_i\to \mathrm{\infty }}{lim}sup\varphi (x_n,x_1)=\varphi (p^{\ast },x_1).\end{array}$$

This shows that ${lim}_{n_i\to \mathrm{\infty }}\varphi (x_{n_i},x_1)=\varphi (p^{\ast },x_1)$, and we have $\parallel x_{n_i}\parallel \to \parallel p^{\ast }\parallel$. Since $x_{n_i}\rightharpoonup p^{\ast }$, by virtue of the Kadec-Klee property of X, we obtain that $x_{n_i}\to p^{\ast }$. Since $\{\varphi (x_n,x_1)\}$ is convergent, this together with ${lim}_{n_i\to \mathrm{\infty }}\varphi (x_{n_i},x_1)=\varphi (p^{\ast },x_1)$ shows that ${lim}_{n_i\to \mathrm{\infty }}\varphi (x_n,x_1)=\varphi (p^{\ast },x_1)$. If there exists some subsequence $\{x_{n_j}\}\subset \{x_n\}$ such that $x_{n_j}\to q$, then from Lemma 2.1 we have

$$\begin{array}{rcl}\varphi (p^{\ast },q)& =& \underset{n_i,n_j\to \mathrm{\infty }}{lim}\varphi (x_{n_i},x_{n_j})=\underset{n_i,n_j\to \mathrm{\infty }}{lim}\varphi (x_{n_i},{\mathrm{\Pi }}_{D_{n_j}}{x}_1)\\ \le & \underset{n_i,n_j\to \mathrm{\infty }}{lim}[\varphi (x_{n_i},x_1)-\varphi ({\mathrm{\Pi }}_{D_{n_j}}{x}_1,x_1)]=\underset{n_i,n_j\to \mathrm{\infty }}{lim}[\varphi (x_{n_i},x_1)-\varphi (x_{n_j},x_1)]\\ =& \varphi (p^{\ast },x_1)-\varphi (p^{\ast },x_1)=0,\end{array}$$

i.e., $p^{\ast }=q$, and hence

$$x_n\to p^{\ast }.$$

(3.4)

By the way, from (3.4), it is easy to see that

$${\xi }_n=v_n\underset{p\in F(T)}{sup}\zeta [\varphi (p,x_n)]+{\mu }_n\to 0.$$

(3.5)

• (IV) Now we prove that $p^{\ast }\in F(T)$.

In fact, since $x_{n+1}\in D_{n+1}$, from (3.1), (3.4) and (3.5), we have

$$\varphi (x_{n+1},y_n)\le {\alpha }_n\varphi (x_{n+1},x_1)+(1-{\alpha }_n)\varphi (x_{n+1},x_n)+{\xi }_n\to 0.$$

(3.6)

Since $x_n\to p^{\ast }$, it follows from (3.6) and Lemma 2.2 that

$$y_n\to p^{\ast }.$$

(3.7)

Since $\{x_n\}$ is bounded and T is a totally quasi-ϕ-asymptotically nonexpansive multi-valued mapping, $T^n{x}_n$ is bounded. In view of ${\alpha }_n\to 0$, from (3.1), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel J{y}_n-J{z}_n\parallel =\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n\parallel J{x}_1-J{z}_n\parallel =0.$$

(3.8)

Since $J{y}_n\to J{p}^{\ast }$, this implies $J{z}_n\to J{p}^{\ast }$. From Remark 1.1, it yields that

$$z_n\rightharpoonup p^{\ast }.$$

(3.9)

Again, since

$$\parallel z_n\parallel -\parallel p^{\ast }\parallel =\parallel J{z}_n\parallel -\parallel J{p}^{\ast }\parallel \le \parallel J{z}_n-J{p}^{\ast }\parallel \to 0,$$

(3.10)

this together with (3.9) and the Kadec-Klee-property of X shows that

$$z_n\to p^{\ast }.$$

(3.11)

On the other hand, by the assumption that T is L-Lipschitz continuous, we have

$$\begin{array}{rcl}d(T{z}_n,z_n)& \le & d(T{z}_n,z_{n+1})+\parallel z_{n+1}-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel +\parallel x_n-z_n\parallel \\ \le & (L+1)\parallel x_{n+1}-x_n\parallel +\parallel z_{n+1}-x_{n+1}\parallel +\parallel x_n-z_n\parallel .\end{array}$$

(3.12)

From (3.11) and $x_n\to p^{\ast }$, we have that $d(T{z}_n,z_n)\to 0$. In view of the closedness of T, it yields that $T(p^{\ast })=\{p^{\ast }\}$, which implies that $p^{\ast }\in F(T)$.

• (V) Finally, we prove that $p^{\ast }={\mathrm{\Pi }}_{F(T)}{x}_1$ and so $x_n\to {\mathrm{\Pi }}_{F(T)}{x}_1$.

Let $w={\mathrm{\Pi }}_{F(T)}{x}_1$. Since $w\in F(T)\subset D_n$, we have $\varphi (p^{\ast },x_1)\le \varphi (w,x_1)$. This implies that

$$\varphi (p^{\ast },x_1)=\underset{n\to \mathrm{\infty }}{lim}\varphi (x_n,x_1)\le \varphi (w,x_1),$$

(3.13)

which yields that $p^{\ast }=w={\mathrm{\Pi }}_{F(T)}{x}_1$. Therefore, $x_n\to {\mathrm{\Pi }}_{F(T)}{x}_1$. The proof of Theorem 3.1 is completed. □

By Remark 2.2, the following corollaries are obtained.

Corollary 3.1 Let X and D be as in Theorem 3.1, and let $T:D\to CB(D)$ be a closed and uniformly L-Lipschitz continuous relatively nonexpansive multi-valued mapping. Let $\{{\alpha }_n\}$ in $(0,1)$ with ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$. Let $\{x_n\}$ be the sequence generated by

$$\{\begin{array}{c}{x}_1\in X\mathit{\text{is arbitrary}};D_1=D,\hfill \\ y_n=J^{-1}[{\alpha }_{n}J{x}_1+(1-{\alpha }_n)J{z}_n],z_n\in T{x}_n,\hfill \\ D_{n+1}=\{z\in D_n:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)\},\hfill \\ x_{n+1}={\mathrm{\Pi }}_{D_{n+1}}{x}_1(n=1,2,\dots ),\hfill \end{array}$$

(3.14)

where $F(T)$ is the set of fixed points of T, and ${\mathrm{\Pi }}_{D_{n+1}}$ is the generalized projection of X onto $D_{n+1}$, then $\{x_n\}$ converges strongly to ${\mathrm{\Pi }}_{F(T)}{x}_1$.

Corollary 3.2 Let X and D be as in Theorem 3.1, and $T:D\to CB(D)$ be a closed and uniformly L-Lipschitz continuous quasi-ϕ-nonexpansive multi-valued mapping. Let $\{{\alpha }_n\}$ be a sequence of real numbers such that ${\alpha }_n\in (0,1)$ for all $n\in N$ and satisfy ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$. Let $\{x_n\}$ be the sequence generated by (3.14). Then $\{x_n\}$ converges strongly to ${\mathrm{\Pi }}_{F(T)}{x}_1$.

Corollary 3.3 Let X be a real uniformly smooth and strictly convex Banach space with the Kadec-Klee property, let D be a nonempty closed convex subset of X, and let $T:D\to CB(D)$ be a closed and uniformly L-Lipschitz continuous quasi-ϕ-asymptotically nonexpansive multi-valued mapping with nonnegative real sequences $\{k_n\}\subset [1,+\mathrm{\infty })$ and $k_n\to 1$ satisfying condition (2.2). Let $\{{\alpha }_n\}$ be a sequence in $(0,1)$ and satisfy ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$. If $\{x_n\}$ is the sequence generated by

$$\{\begin{array}{c}{x}_1\in X\mathit{\text{is arbitrary}};D_1=D,\hfill \\ y_n=J^{-1}[{\alpha }_{n}J{x}_1+(1-{\alpha }_n)J{z}_n],z_n\in T^n{x}_n,\hfill \\ D_{n+1}=\{z\in D_n:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)+{\xi }_n\},\hfill \\ x_{n+1}={\mathrm{\Pi }}_{D_{n+1}}{x}_1(n=1,2,\dots ),\hfill \end{array}$$

(3.15)

where ${\xi }_n=(k_n-1){sup}_{p\in F(T)}\varphi (p,x_n)$, $F(T)$ is the fixed point set of T, and ${\mathrm{\Pi }}_{D_{n+1}}$ is the generalized projection of X onto $D_{n+1}$, if $F(T)$ is nonempty, then $\{x_n\}$ converges strongly to ${\mathrm{\Pi }}_{F(T)}{x}_1$.

4 Application

We utilize Corollary 3.2 to study a modified Halpern iterative algorithm for a system of equilibrium problems.

Theorem 4.1 Let D, X and $\{{\alpha }_n\}$ be the same as in Theorem 3.1. Let $f:D\times D\to R$ be a bifunction satisfying conditions (A1)-(A4) as given in Example 2.1. Let $T_r:X\to D$ be a mapping defined by (2.1), i.e.,

$$T_r(x)=\{x\in D,f(z,y)+\frac{1}{r}〈y-z,Jz-Jx〉\ge 0,\mathrm{\forall }y\in D\},\mathrm{\forall }x\in X.$$

Let $\{x_n\}$ be the sequence generated by

$$\{\begin{array}{c}{x}_1\in X\mathit{\text{is arbitrary}};D_1=D,\hfill \\ f(u_n,y)+\frac{1}{r}〈y-u_n,J{u}_n-J{x}_n〉\ge 0,\mathrm{\forall }y\in D,r>0,u_n\in T_r{x}_n,\hfill \\ y_n=J^{-1}[{\alpha }_{n}J{x}_1+(1-{\alpha }_n)J{u}_n],\hfill \\ D_{n+1}=\{z\in D_n:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)\},\hfill \\ x_{n+1}={\prod }_{D_{n+1}}{x}_1(n=1,2,\dots ).\hfill \end{array}$$

(4.1)

If $F(T_r)\ne \mathrm{\Phi }$, then $\{x_n\}$ converges strongly to ${\prod }_{F(T)}{x}_1$, which is a common solution of the system of equilibrium problems for f.

Proof In Example 2.1, we have pointed out that $u_n=T_r(x_n)$, $F(T_r)=EP(f)$ and $T_r$ is a closed quasi-ϕ-nonexpansive mapping. Hence (4.1) can be rewritten as follows:

$$\{\begin{array}{c}{x}_1\in X\text{is arbitrary};D_1=D,\hfill \\ y_n=J^{-1}[{\alpha }_{n}J{x}_1+(1-{\alpha }_n)J{u}_n],u_n\in T_r{x}_n,\hfill \\ D_{n+1}=\{z\in D_n:\varphi (z,y_n)\le {\alpha }_n\varphi (z,x_1)+(1-{\alpha }_n)\varphi (z,x_n)\},\hfill \\ x_{n+1}={\prod }_{D_{n+1}}{x}_1(n=1,2,\dots ).\hfill \end{array}$$

(4.2)

Therefore the conclusion of Theorem 4.1 can be obtained from Corollary 3.2. □