A new graph based on the semi-direct product of some monoids

Abstract

In this paper, firstly, we define a new graph based on the semi-direct product of a free abelian monoid of rank n by a finite cyclic monoid, and then discuss some graph properties on this new graph, namely diameter, maximum and minimum degrees, girth, degree sequence and irregularity index, domination number, chromatic number, clique number of $\mathrm{\Gamma }({\mathcal{P}}_M)$. Since graph theoretical studies (including such above graph parameters) consist of some fixed point techniques, they have been applied in fields such as chemistry (in the meaning of atoms, molecules, energy etc.) and engineering (in the meaning of signal processing etc.), game theory and physics.

MSC:05C10, 05C12, 05C25, 20E22, 20M05.

1 Introduction and preliminaries

In this paper, we mainly investigate the interplay between the semi-direct product over monoids and the graph-theoretic properties of the semi-direct product in terms of its relations. In detailed, let us consider a free abelian monoid $F_n$ of rank n and also consider a finite cyclic monoid C. Then, by [1], we can define the semi-direct product of $F_n$ by C. Moreover, one can also define a new graph associated with this semi-direct product (see Section 1.1 below). Thus the idea in here is to present the interplay between the algebraic semigroup and graph-theoretic properties of this new graph. In fact, by the graph-theoretic properties, we will be interested in the diameter, maximum and minimum degrees, girth, chromatic number, clique number, domination number, degree sequence and irregularity index of the corresponding new graph. In the literature, there are some important graph varieties and works that are related to algebraic and topological structures, namely, Cayley graphs [2–4] or zero-divisor graphs [5–7]. But the graph constructed in here is different from those in the previous studies and is also interesting in terms of using algebraic semi-direct products during the construction of the vertex and edge sets. So, this kind of graph not only provides the classification of algebras (monoids, semigroups), but also solves the problems of normal forms of elements, word problem, rewriting system, embedding theorems, extensions of groups and algebras, growth function, Hilbert series, etc. As is well known, these problems are really important in fixed point results since they have a direct connection to nature sciences.

First of all, let us recall the semi-direct product of any two monoids and its presentation. Thus, let us take two arbitrary monoids A and K with associated presentations ${\mathcal{P}}_A=[X;\mathbf{r}]$ and ${\mathcal{P}}_K=[Y;\mathbf{s}]$, respectively. Also, let $M=K{⋊}_{\theta }A$ be the corresponding semi-direct product of these two monoids, where θ is a monoid homomorphism from A to $End(K)$. We note that the reader can find some examples of monoid endomorphisms in [8]. The elements of M can be regarded as ordered pairs $(a,k)$, where $a\in A$, $k\in K$ with multiplication given by $(a,k)(a^{\mathrm{\prime }},k^{\mathrm{\prime }})=(a{a}^{\mathrm{\prime }},(k{\theta }_{a^{\mathrm{\prime }}})k^{\mathrm{\prime }})$. The monoids A and K are identified with the submonoids of M having elements $(a,1)$ and $(1,k)$, respectively. Furthermore, one can define a standard presentation for M as follows: For every $x\in X$ and $y\in Y$, choose a word, which we denote by $y{\theta }_x$, on Y such that $[y{\theta }_x]=[y]{\theta }_{[x]}$ as an element of K. To establish notation, let us denote the relation $yx=x(y{\theta }_x)$ on $X\cup Y$ by $T_{yx}$ and write t for the set of relations $T_{yx}$. Then

$${\mathcal{P}}_M=[Y,X;\mathbf{s},\mathbf{r},\mathbf{t}]$$

is a standard monoid presentation for the semi-direct product M. We may refer to [9, 10] for more detailed knowledge about the definition and a standard presentation for the semi-direct product of two monoids.

Let $F_n$ and C be a free abelian monoid of rank n and a finite cyclic monoid with the presentations

$${\mathcal{P}}_{F_n}=〈y_1,y_2,\dots ,y_n;y_i{y}_j=y_j{y}_i(1\le i<j\le n)〉$$

and

$${\mathcal{P}}_C=〈x;x^k=x^l(1\le l<k)〉,$$

respectively. By [1], if one considers the matrix

$$\mathcal{M}=\left[\begin{array}{cccc}{\alpha }_{11}& {\alpha }_{12}& \cdots & {\alpha }_{1n}\\ {\alpha }_{21}& {\alpha }_{22}& \cdots & {\alpha }_{2n}\\ ⋮& \ddots & ⋮\\ {\alpha }_{n1}& {\alpha }_{n2}& \cdots & {\alpha }_{nn}\end{array}\right]$$

and assumes ${\mathcal{M}}^k\equiv {\mathcal{M}}^l$ (modd), where $d\mid (k-l)$, then there exits a semi-direct product $M=F_n{⋊}_{\theta }C$ with the presentation

$$\begin{array}{rcl}{\mathcal{P}}_M& =& 〈y_1,y_2,\dots ,y_n,x;y_i{y}_j=y_j{y}_i(1\le i<j\le n),x^k=x^l,\\ y_{1}x=x{y}_1^{{\alpha }_{11}}{y}_2^{{\alpha }_{12}}\cdots y_n^{{\alpha }_{1n}},y_{2}x=x{y}_1^{{\alpha }_{21}}{y}_2^{{\alpha }_{22}}\cdots y_n^{{\alpha }_{2n}},\dots ,\\ y_{n}x=x{y}_1^{{\alpha }_{n1}}{y}_2^{{\alpha }_{n2}}\cdots y_n^{{\alpha }_{nn}}〉.\end{array}$$

(1)

1.1 A new graph based on semi-direct products

In the following, we define an undirected graph $\mathrm{\Gamma }({\mathcal{P}}_M)=(V,E)$ associated with ${\mathcal{P}}_M$ given in (1). Actually, all the results presented in this paper are based on this graph.

The vertex set V consists of the following:

• all generators $y_i$ ($1\le i\le n$) and x of ${\mathcal{P}}_M$,

• words of the form $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ ($1\le i\le n$) in the presentation (1),

• words of the form $y_i{y}_{i+1}$ ($1\le i\le n-1$) in (1). (Here, we omitted the words of the remaining format. In other words, we do not take $y_i{y}_{i+2}$, $y_i{y}_{i+3}$, etc. as a vertex in our set),

• word of the form $x^k$ if $l\ne 1$ in the presentation (1). Otherwise, i.e., if $l=1$ then we have a relator $x^k=x$; in that case, since x is in the vertex set, there is no need to take $x^k$ as a vertex.

The edge E consists of the following:

• connect each vertex $y_i$ to single x for all $1\le i\le n$,

• connect each of the adjacent vertices $y_i$ and $y_{i+1}$ for all $1\le i\le n-1$,

• connect each vertex $y_i$ to the related vertices $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ for all $1\le i\le n$,

• connect each of the vertices $y_i$ and $y_{i+1}$ to the vertex $y_i{y}_{i+1}$ from both sides for all $1\le i\le n-1$,

• connect the unique vertex x to each vertex of the form $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ for all $1\le i\le n$.

Remark 1

• (a) In the construction of the semi-direct product, we assume that all rows of the matrix ℳ are different from each other. This affects our matching in the graph as all vertices $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$’s are distinct.

• (b) To simplify, let us label the vertex

  

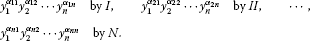
• (c) As seen in Figure 1, the number of vertex and edge sets depends on the number of generators of the free abelian monoid of rank n. Thus we have

  

Figure 1

The graph $\mathbf{\Gamma }\mathbf{(}{\mathcal{P}}_{\mathit{M}}\mathbf{)}$ .

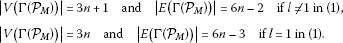
Thus we obtain the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$ as drawn in Figure 1.

2 Graph theoretical results over $\mathrm{\Gamma }({\mathcal{P}}_M)$

In this section, by considering the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$ drawn in Figure 1, we mainly deal with some graph properties, namely diameter, maximum and minimum degrees, girth, degree sequence, irregularity index, domination number, chromatic number and clique number of $\mathrm{\Gamma }({\mathcal{P}}_M)$.

We first recall that for any simple graph Γ, the distance (length of the shortest path) between two vertices u, v of Γ is denoted by $d_{\mathrm{\Gamma }}(u,v)$. If no such path exists, we set $d(x,y):=\mathrm{\infty }$. Actually, the diameter of Γ is defined by

$$diam(\mathrm{\Gamma })=sup\{d_{\mathrm{\Gamma }}(x,y):x\text{ and }y\text{ are vertices of }\mathrm{\Gamma }\}.$$

We thus get the following result.

Theorem 1 The diameter of the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$ is 3.

Proof By Figure 1, it is clearly seen that the vertex $x^k$ (if $l\ne 1$ then it exists in the graph) of $\mathrm{\Gamma }({\mathcal{P}}_M)$ is pendant and so the diameter can be figured out by considering the distance $d_{\mathrm{\Gamma }({\mathcal{P}}_M)}(x^k,y)$, where y is one of the other vertices. If $l=1$ in the presentation (1), then the vertex x is pendant of the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$. By Figure 1, we also see that the vertex x is connected with all the vertices except the vertices of the form $y_i{y}_{i+1}$ ($1\le i\le n-1$) in the vertex set. Thus we can reach these vertices by only one edge from the vertices $y_i$ ($1\le i\le n$). So, we get $diam(\mathrm{\Gamma }({\mathcal{P}}_M))=3$. □

The degree ${deg}_{\mathrm{\Gamma }}(v)$ of a vertex v of Γ is the number of vertices adjacent to v. Among all degrees, the maximum degree $\mathrm{\Delta }(\mathrm{\Gamma })$ (or the minimum degree $\delta (\mathrm{\Gamma })$) of Γ is the number of the largest (or the smallest) degrees in Γ (see [11]). In our graph, maximum and minimum degrees are obtained as follows.

Theorem 2 The maximum and minimum degrees of the graphs $\mathrm{\Gamma }({\mathcal{P}}_M)$ are

$$\mathrm{\Delta }(\mathrm{\Gamma }({\mathcal{P}}_M))=\{\begin{array}{cc}2n+1;\hfill & \mathit{\text{if}}l\ne 1\mathit{\text{in}}\text{ (1)},\hfill \\ 2n;\hfill & \mathit{\text{if}}l=1\mathit{\text{in}}\text{ (1)}\hfill \end{array}\mathit{\text{and}}\delta (\mathrm{\Gamma }({\mathcal{P}}_M))=\{\begin{array}{cc}1;\hfill & \mathit{\text{if}}l\ne 1\mathit{\text{in}}\text{ (1)},\hfill \\ 2;\hfill & \mathit{\text{if}}l=1\mathit{\text{in}}\text{ (1),}\hfill \end{array}$$

respectively.

Proof By Figure 1, it is seen that the vertex x is connected with all vertices of the form $y_i$ ($1\le i\le n$), $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ ($1\le i\le n$) and the vertex $x^k$ if $l\ne 1$ in the presentation (1). So, $\mathrm{\Delta }(\mathrm{\Gamma }({\mathcal{P}}_M))=n+n+1=2n+1$. In the case $l=1$ in the presentation (1), since there is no vertex labeled by $x^k$, we get $\mathrm{\Delta }(\mathrm{\Gamma }({\mathcal{P}}_M))=n+n=2n$.

On the other hand, if $l\ne 1$ in the presentation (1), then there is only one edge from the vertex $x^k$ to the vertex x. Thus $\delta (\mathrm{\Gamma }({\mathcal{P}}_M))=1$. Otherwise, since the vertices which are of the form $y_i{y}_{i+1}$ ($1\le i\le n-1$) are connected to the vertices $y_i$ and $y_{i+1}$, we get $\delta (\mathrm{\Gamma }({\mathcal{P}}_M))=2$, as required. □

It is known that the girth of a simple graph Γ is the length of the shortest cycle contained in Γ. However, if the graph does not contain any cycle, then the girth of it is assumed to be infinity. Hence the other result of this section is the following.

Theorem 3 The girth of the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$ is 3.

Proof By the edge definition of $\mathrm{\Gamma }({\mathcal{P}}_M)$, the vertex x is connected to the vertices of the form $y_i$ ($1\le i\le n$) and $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ ($1\le i\le n$). There also exists an edge between vertices $y_i$ and $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$. So, the length of the shortest cycle contained in the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$ is 3. □

There also exists the term degree sequence $DS(\mathrm{\Gamma })$, which is a sequence of degrees of vertices of the graph Γ. Recently, in [12], a new parameter for graphs, namely the irregularity index of Γ, has been defined and denoted by $\mathit{MWB}(\mathrm{\Gamma })$. In fact $\mathit{MWB}(\mathrm{\Gamma })$ is the number of distinct terms in the set $DS(\mathrm{\Gamma })$.

Theorem 4 The degree sequence and irregularity index of $\mathrm{\Gamma }({\mathcal{P}}_M)$ are given by

$$DS(\mathrm{\Gamma }({\mathcal{P}}_M))=\{\begin{array}{cc}(1,\underset{2n-1\mathit{times}}{\underbrace{2,2,\dots ,2}},4,4,\underset{n-2\mathit{times}}{\underbrace{6,6,\dots ,6}},2n);\hfill & \mathit{\text{if}}l\ne 1,\hfill \\ (\underset{2n-1\mathit{times}}{\underbrace{2,2,\dots ,2}},4,4,\underset{n-2\mathit{times}}{\underbrace{6,6,\dots ,6}},2n);\hfill & \mathit{\text{if}}l=1\hfill \end{array}$$

and

$$\mathit{MWB}(\mathrm{\Gamma }({\mathcal{P}}_M))=\{\begin{array}{cc}3;\hfill & \mathit{\text{if}}l\ne 1\mathit{\text{and}}n=2,\hfill \\ 4;\hfill & \mathit{\text{if}}l\ne 1\mathit{\text{and}}n\ge 3,\hfill \\ 2;\hfill & \mathit{\text{if}}l=1\mathit{\text{and}}n=2,\hfill \\ 3;\hfill & \mathit{\text{if}}l=1\mathit{\text{and}}n=3,\hfill \\ 4;\hfill & \mathit{\text{if}}l=1\mathit{\text{and}}n\ge 4,\hfill \end{array}$$

respectively.

Proof Let us consider the case $l\ne 1$ in the presentation (1). In this case, since the vertex $x^k$ is connected with only the vertex x, then we clearly obtain that the degree of $x^k$ is 1. Now we consider the vertices of the form $y_i{y}_{i+1}$ ($1\le i\le n-1$) and $y_1^{{\alpha }_{j1}}{y}_2^{{\alpha }_{j2}}\cdots y_n^{{\alpha }_{jn}}$ ($1\le j\le n$). Since these vertices are connected with the vertices $y_i$, $y_{i+1}$ ($1\le i\le n-1$) and $y_j$ ($1\le j\le n$), x, the degree of them is 2. Thus we have $2n-1$ vertices which have degree 2. By Figure 1, we see that the vertices $y_1$ and $y_n$ are connected to $y_1{y}_2$, $y_2$, $y_1^{{\alpha }_{11}}{y}_2^{{\alpha }_{12}}\cdots y_n^{{\alpha }_{1n}}$, x and $y_{n-1}{y}_n$, $y_{n-1}$, $y_1^{{\alpha }_{n1}}{y}_2^{{\alpha }_{n2}}\cdots y_n^{{\alpha }_{nn}}$, x, respectively. So, the degree of $y_1$ and $y_n$ is 4. The remaining vertices $y_i$ ($2\le i\le n-1$) are connected to the vertices $y_i$, $y_{i-1}{y}_i$, $y_i{y}_{i+1}$, $y_{i+1}$, $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ and x. So, the degree of them is 6. Since the reminded vertex x is connected with $y_i$, $y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}$ ($1\le i\le n$) and $x^k$ the degree of it is $2n+1$. Now, let us consider the case $l=1$ in the presentation (1). In this case, since the vertex $x^k$ does not exist, we get the degree sequence $DS(\mathrm{\Gamma }({\mathcal{P}}_M))$ as depicted in the theorem.

For $\mathit{MWB}(\mathrm{\Gamma }({\mathcal{P}}_M))$, we need to consider the number n in the presentation (1). The number of distinct terms in the set $DS(\mathrm{\Gamma }({\mathcal{P}}_M))$ depends on the number n. By considering the number n, we can easily obtain the irregularity index $\mathit{MWB}(\mathrm{\Gamma }({\mathcal{P}}_M))$, as required. □

A subset D of the vertex set $V(\mathrm{\Gamma })$ of a graph Γ is called a dominating set if every vertex $V(\mathrm{\Gamma })\mathrm{\setminus }D$ is joined to at least one vertex of D by an edge. Additionally, the domination number $\gamma (\mathrm{\Gamma })$ is the number of vertices in the smallest dominating set for the graph Γ (see [11]).

Theorem 5 The domination number of $\mathrm{\Gamma }({\mathcal{P}}_M)$ is given by

$$\gamma (\mathrm{\Gamma }({\mathcal{P}}_M))=\{\begin{array}{cc}\frac{n+2}{2};\hfill & n\mathit{\text{is even}},\hfill \\ \frac{n+1}{2};\hfill & n\mathit{\text{is odd}}.\hfill \end{array}$$

Proof By considering Figure 1, the vertex x is adjacent to all the vertices except the vertex of the form $y_i{y}_{i+1}$ ($1\le i\le n-1$). Thus, in the domination set, there must be some vertices of the form $y_i$ adjacent to the vertices of the form $y_i{y}_{i+1}$. These vertices depend on the number of n in the presentation (1). If n is even, then there are $\frac{n}{2}+1$ vertices ($y_2,y_4,\dots ,y_n,x$) in the smallest dominating set for $\mathrm{\Gamma }({\mathcal{P}}_M)$. Otherwise, there are $\frac{n-1}{2}+1$ vertices. Hence the result. □

Basically, the coloring of a graph Γ is to be an assignment of colors (elements of some set) to the vertices of Γ, one color to each vertex, so that adjacent vertices are assigned distinct colors. If n colors are used, then the coloring is referred to as n-coloring. If there exists an n-coloring of Γ, then Γ is called n-colorable. The minimum number n for which Γ is n-colorable is called the chromatic number of Γ and is denoted by $\chi (\mathrm{\Gamma })$. There exists another graph parameter, namely the clique of a graph Γ. In fact, depending on the vertices, each of the maximal complete subgraphs of Γ is called a clique. Moreover, the largest number of vertices in any clique of Γ is called the clique number and is denoted by $\omega (\mathrm{\Gamma })$. In general, it is well known that $\chi (\mathrm{\Gamma })\ge \omega (\mathrm{\Gamma })$ for any graph Γ (for instance [11]).

Theorem 6 The chromatic number $\chi (\mathrm{\Gamma }({\mathcal{P}}_M))$ is equal to 3.

Proof Let us consider the vertex x in the graph $\mathrm{\Gamma }({\mathcal{P}}_M)$ drawn in Figure 1. It is easy to see that x is adjacent to all the other vertices except the vertices of the form $y_i{y}_{i+1}$ ($1\le i\le n-1$). That means the color used for the vertex x can be used for the vertices $y_i{y}_{i+1}$. Thus let us suppose that the color for x and $y_i{y}_{i+1}$ is labeled by ${\mathcal{C}}_1$. Next, let us consider the vertices $y_i$ ($1\le i\le n$) in Figure 1. Since these vertices are connected with each other doubly, we have two different colors labeled by ${\mathcal{C}}_2$ and ${\mathcal{C}}_3$. In other words, if we label the vertex $y_1$ by ${\mathcal{C}}_2$, then we label the vertex $y_2$ by ${\mathcal{C}}_3$, $y_3$ by ${\mathcal{C}}_2$ and so on. Now we take account of vertices $I,II,\dots ,N$. Since these vertices are adjacent to the vertices $y_1,y_2,\dots ,y_n$, respectively, they can be labeled by ${\mathcal{C}}_3$ and ${\mathcal{C}}_2$, respectively. Since the remaining vertex $x^k$ is just connected with the vertex x, it can be labeled by ${\mathcal{C}}_2$. Hence the result. □

We note that the chromatic number of $\mathrm{\Gamma }({\mathcal{P}}_M)$ does not depend on the number of generators of the free abelian monoid of rank n.

Theorem 7 The clique number $\omega (\mathrm{\Gamma }({\mathcal{P}}_M))$ is equal to 3.

Proof By Figure 1, we have three types of maximal complete subgraphs of $\mathrm{\Gamma }({\mathcal{P}}_M)$. These types consist of the following edges which have three vertices: $y_i-y_{i+1}-y_i{y}_{i+1}-y_i$, $y_i-y_{i+1}-x-y_i$ and $y_i-y_1^{{\alpha }_{i1}}{y}_2^{{\alpha }_{i2}}\cdots y_n^{{\alpha }_{in}}-x-y_i$. Hence the result. □

Example 1 Let us consider a free abelian monoid of rank 3, $F_3$, and a finite cyclic monoid C with the presentations

$${\mathcal{P}}_{F_3}=〈y_1,y_2,y_3;y_1{y}_2=y_2{y}_1,y_2{y}_3=y_3{y}_2,y_1{y}_3=y_3{y}_1〉$$

and ${\mathcal{P}}_C=〈x;x^4=x^2〉$, respectively. By taking the matrix

$$\mathcal{M}=\left[\begin{array}{ccc}1& 2& 3\\ 2& 3& 1\\ 3& 1& 2\end{array}\right]$$

and the homomorphism $\theta :C\to End(F_3)$, we can get a semi-direct product $F_3{⋊}_{\theta }C$ with the presentation

$$\begin{array}{rcl}{\mathcal{P}}_{F_3{⋊}_{\theta }C}& =& 〈y_1,y_2,y_3,x;y_1{y}_2=y_2{y}_1,y_2{y}_3=y_3{y}_2,y_1{y}_3=y_3{y}_1,x^4=x^2,\\ y_{1}x=x{y}_1{y}_2^2{y}_3^3,y_{2}x=x{y}_1^2{y}_2^3{y}_3,y_{3}x=x{y}_1^3{y}_2{y}_3^2〉.\end{array}$$

(2)

By considering the presentation in (2) and Figure 2, we have the following:

• $$V(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=\{y_1,y_2,y_3,x,x^4,y_1{y}_2,y_2{y}_3,y_1{y}_2^2{y}_3^3,y_1^2{y}_2^3{y}_3,y_1^3{y}_2{y}_3^2\}$$

  and so $|V(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))|=3.3+1=10$.

• $$E(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=\{e_i(1\le i\le 16),\text{ in Figure 2}\}$$

  and so $|E(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))|=6.3-2=16$.

Figure 2

The graph defined in Example 1.

• $$diam(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=3$$

  .

• $$\mathrm{\Delta }(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=2.3+1=7$$

  and $\delta (\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=1$.

• $$girth(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=3$$

  .

• $$DS(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=(1,2,2,2,2,2,4,4,6)$$

  and so $\mathit{MWB}(\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=4$.

• $$\gamma (\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=\frac{3+1}{2}=2$$

  .

• $$\chi (\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=\omega (\mathrm{\Gamma }({\mathcal{P}}_{F_3{⋊}_{\theta }C}))=3$$

  .