Coupled coincidence point theorems in (intuitionistic) fuzzy normed spaces

Abstract

In this paper, we prove some coupled coincidence point theorems in fuzzy normed spaces. Our results improve and restate the proof lines of the main results given in the papers (Eshaghi Gordji et al. in Math. Comput. Model. 54:1897-1906, 2011) and (Sintunavarat et al. in Fixed Point Theory Appl. 2011:81, 2011).

MSC:47H10, 54H25, 34B15.

1 Introduction

Recently, many authors have shown the existence of coupled fixed points and common fixed points for some contractions in cone metric spaces, partially ordered metric spaces, fuzzy metric spaces, fuzzy normed spaces, intuitionistic fuzzy normed spaces and others ([1–11]).

Especially in [11], Sintunavarat et al. proved some coupled fixed point theorems for contractive mappings in partially complete intuitionistic fuzzy normed spaces, which extended and improved coupled coincidence point theorems in Gordji et al. [5]. But the authors found some mistakes in the proof lines of the main result (Theorem 2.5) of [5] and the same mistakes in [11].

In Section 2 of this paper, we restate some definitions and the main results in [11]. In Section 3, we give some comments about the incorrect proof lines of the main results given in [5] and [11] and explain why the lines of the proofs are wrong. Finally, in Section 4, we extend and improve some coupled fixed point theorems.

2 Preliminaries

A t-norm (resp., a t-conorm) is a mapping $\ast :{[0,1]}^2\to [0,1]$ (resp., $\diamond :{[0,1]}^2\to [0,1]$) that is associative, commutative and non-decreasing in both arguments and has 1 (resp., 0) as identity.

Definition 2.1 [9]

A fuzzy normed space (in brief, FNS) is a triple $(X,\mu ,\ast )$, where X is a vector space, ∗ is a continuous t-norm and $\mu :X\times (0,\mathrm{\infty })\to [0,1]$ is a fuzzy set such that, for all $x,y\in X$ and $t,s>0$,

(F1) $\mu (x,t)>0$;

(F2) $\mu (x,t)=1$ for all $t>0$ if and only if $x=0$;

(F3) $\mu (\alpha x,t)=\mu (x,\frac{t}{|\alpha |})$ for all $\alpha \ne 0$;

(F4) $\mu (x,t)\ast \mu (y,s)\le \mu (x+y,t+s)$;

(F5) $\mu (x,\cdot ):(0,\mathrm{\infty })\to [0,1]$ is continuous;

(F6) ${lim}_{t\to \mathrm{\infty }}\mu (x,t)=1$ and ${lim}_{t\to 0}\mu (x,t)=0$.

Using the continuous t-norms and t-conorms, Saadati and Park [12] introduced the concept of an intuitionistic fuzzy normed space.

Definition 2.2 An intuitionistic fuzzy normed space (in brief, IFNS) is a 5-tuple $(X,\mu ,\nu ,\ast ,\diamond )$ where X is a vector space, ∗ is a continuous t-norm, ⋄ is a continuous t-conorm and $\mu ,\nu :X\times (0,\mathrm{\infty })\to [0,1]$ are fuzzy sets such that, for all $x,y\in X$ and $t,s>0$,

(IF1) $\mu (x,t)+\nu (x,t)\le 1$;

(IF2) $\mu (x,t)>0$ and $\nu (x,t)<1$;

(IF3) $\mu (x,t)=1$ for all $t>0$ if and only if $x=0$ if and only if $\nu (x,t)=0$ for all $t>0$;

(IF4) $\mu (\alpha x,t)=\mu (x,\frac{t}{|\alpha |})$ and $\nu (\alpha x,t)=\nu (x,\frac{t}{|\alpha |})$ for all $\alpha \ne 0$;

(IF5) $\mu (x,t)\ast \mu (y,s)\le \mu (x+y,t+s)$ and $\nu (x,t)\diamond \nu (y,s)\ge \nu (x+y,t+s)$;

(IF6) $\mu (x,\cdot ),\nu (x,\cdot ):(0,\mathrm{\infty })\to [0,1]$ are continuous;

(IF7) ${lim}_{t\to \mathrm{\infty }}\mu (x,t)=1={lim}_{t\to 0}\nu (x,t)$ and ${lim}_{t\to 0}\mu (x,t)=0={lim}_{t\to \mathrm{\infty }}\nu (x,t)$.

Obviously, if $(X,\mu ,\nu ,\ast ,\diamond )$ is an IFNS, then $(X,\mu ,\ast )$ is an FNS. We refer to this space as its support.

Lemma 2.1 $\mu (x,\cdot )$ is a non-decreasing function on $(0,\mathrm{\infty })$ and $\nu (x,\cdot )$ is a non-increasing function on $(0,\mathrm{\infty })$.

Some properties and examples of IFNS and the concepts of convergence and a Cauchy sequence in IFNS are given in [12].

Definition 2.3 [12]

Let $(X,\mu ,\nu ,\ast ,\diamond )$ be an IFNS.

• (1) A sequence $\{x_n\}\subset X$ is called a Cauchy sequence if, for any $ϵ>0$ and $t>0$, there exists $n_0\in \mathbb{N}$ such that $\mu (x_n-x_m,t)>1-ϵ$ and $\nu (x_n-x_m,t)<ϵ$ for all $n,m\ge n_0$.

• (2) A sequence $\{x_n\}\subset X$ is said to be convergent to a point $x\in X$ denoted by $x_n\to x$ or by ${lim}_{n\to \mathrm{\infty }}{x}_n=x$ if, for any $ϵ>0$ and $t>0$, there exists $n_0\in \mathbb{N}$ such that $\mu (x_n-x,t)>1-ϵ$ and $\nu (x_n-x,t)<ϵ$ for all $n\ge n_0$.

• (3) An IFNS in which every Cauchy sequence is convergent is said to be complete.

Most of the following definitions were introduced in [8].

Definition 2.4 Let $F:X\times X\to X$ and $g:X\to X$ be two mappings.

• (1) F and g are said to be commuting if $gF(x,y)=F(gx,gy)$ for all $x,y\in X$.

• (2) A point $(x,y)\in X\times X$ is called a coupled coincidence point of the mappings F and g if $F(x,y)=gx$ and $F(y,x)=gy$. If g is the identity, $(x,y)$ is called a coupled fixed point of F.

• (3) If $(X,⊑)$ is a partially ordered set, then F is said to have the mixed g-monotone property if it verifies the following properties:

  

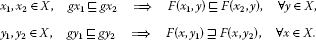
If g is the identity mapping, then F is said to have the mixed monotone property.

• (4) If $(X,⊑)$ is a partially ordered set, then X is said to have the sequential g-monotone property if it verifies the following properties:

(B1) If $\{x_n\}$ is a non-decreasing sequence and ${lim}_{n\to \mathrm{\infty }}{x}_n=x$, then $g{x}_n⊑gx$ for all $n\in \mathbb{N}$.

(B2) If $\{x_n\}$ is a non-increasing sequence and ${lim}_{n\to \mathrm{\infty }}{y}_n=y$, then $g{y}_n⊒gy$ for all $n\in \mathbb{N}$.

If g is the identity mapping, then X is said to have the sequential monotone property.

Definition 2.5 Let X and Y be two IFNS. A function $f:X\to Y$ is said to be continuous at a point $x_0\in X$ if, for any sequence $\{x_n\}$ in X converging to $x_0$, the sequence $\{f(x_n)\}$ in Y converges to $f(x_0)$. If f is continuous at each $x\in X$, then f is said to be continuous on X.

Definition 2.6 [5]

Let $(X,\mu ,\nu ,\ast ,\diamond )$ be an IFNS. The pair $(\mu ,\nu )$ is said to satisfy the n-property on $X\times (0,\mathrm{\infty })$ if ${lim}_{n\to \mathrm{\infty }}{[\mu (x,k^{n}t)]}^{n^p}=1$ and ${lim}_{n\to \mathrm{\infty }}{[\nu (x,k^{n}t)]}^{n^p}=0$ whenever $x\in X$, $k>1$ and $p>0$.

The following lemma proved by Haghi et al. [7] is useful for our main results.

Lemma 2.2 Let X be a nonempty set and $g:X\to X$ be a mapping. Then there exists a subset $E\subset X$ such that $g(E)=g(X)$ and $g:E\to X$ is one-to-one.

In order to state our results, we give the main results given in [5] and [11].

Lemma 2.3 [[5], Lemma 2.1]

Let $(X,\mu ,\nu ,\ast ,\diamond )$ be an IFNS. Let $a\ast b\ge ab$, $a\diamond b\le ab$ for all $a,b\in [0,1]$ and $(\mu ,\nu )$ satisfy the n-property. Suppose that $\{x_n\}$ is a sequence in X such that

$$\mu (x_{n+1}-x_n,kt)\ge \mu (x_n-x_{n-1},t),\nu (x_{n+1}-x_n,kt)\le \nu (x_n-x_{n-1},t)$$

for all $t>0$ and $n\in \mathbb{N}$, where $0<k<1$. Then the sequence $\{x_n\}$ is a Cauchy sequence in X.

Theorem 2.4 ([[5], Theorem 2.5], [[11], Theorem 3.1])

Let $(X,⊑)$ be a partially ordered set and suppose that $a\diamond b\le ab\le a\ast b$ for all $a,b\in [0,1]$. Let $(X,\mu ,\nu ,\ast ,\diamond )$ be a complete IFNS such that $(\mu ,\nu )$ has the n-property. Let $F:X\times X\to X$ and $g:X\to X$ be two mappings such that F has the mixed g-monotone property and

for which $gx⊑gu$ and $gy⊒gv$, where $0<k<1$, $F(X\times X)\subseteq g(X)$ and g is continuous. Suppose either

• (a) F is continuous or

• (b) X has the sequential g-monotone property.

If there exist $x_0,y_0\in X$ such that $g{x}_0⊑F(x_0,y_0)$ and $g{y}_0⊒F(y_0,x_0)$, then there exist $x,y\in X$ such that $gx=F(x,y)$ and $gy=F(y,x)$.

3 Comments and suggestions

In this section, we show that the conditions of the above Lemma 2.3 and Theorem 2.4 in [5] are inadequate and, furthermore, the proof lines of Theorem 2.4 are not correct. We also would like to point out that the results in [5] can be corrected under the appropriate conditions on the t-norm and the FNS.

First of all, in the conditions of Lemma 2.3 and Theorem 2.4, we have a t-conorm ⋄ such that $a\diamond b\le ab$ for all $a,b\in [0,1]$. If we take $b=0$, then $a=a\diamond 0\le 0$ for all $a\in [0,1]$. It is obviously impossible. Moreover, it is well known and easy to see that if ∗ is a t-norm and ⋄ is a t-conorm, then $a\ast b\le a\diamond b$ for all $a,b\in [0,1]$. In this sense, Lemma 2.3 and Theorem 2.4 have to be corrected.

Secondly, from the property (IF1), it follows that a sequence $\{x_n\}\subset X$ is a Cauchy sequence if, for any $ϵ>0$ and $t>0$, there exists $n_0\in \mathbb{N}$ such that $\mu (x_n-x_m,t)>1-ϵ$ for all $n,m\ge n_0$. That is, the sequence $\{x_n\}\subset X$ is a Cauchy sequence on the IFNS $(X,\mu ,\nu ,\ast ,\diamond )$ if it also is on the FNS $(X,\mu ,\ast )$. A similar comment is valid for the convergence.

Furthermore, the completeness of an IFNS is equivalent to the completeness of its support FNS and so we can deduce any fixed point theorem for IFNS (when the conditions on μ and ν are splitting) as an immediate consequence of its associated fixed point theorem for FNS. In particular, it is sufficient to prove Theorem 2.4 just for FNS. Therefore, we only develop Theorem 4.2 for FNS.

Also, some proof lines of Lemma 2.3 are not correct (see p.1900, lines 9-23):

$$\begin{array}{rcl}\mu (x_n-x_m,t)& \ge & {\left[\mu (x_0-x_1,(1-k)\frac{t}{k^n})\right]}^m\\ \ge & {\left[\mu (x_0-x_1,(1-k)\frac{t}{k^n})\right]}^{n^q}\to 1,\end{array}$$

where $q>0$ such that $m<n^q$, and

$$\begin{array}{rcl}\nu (x_n-x_m,t)& \le & {\left[\nu (x_0-x_1,(1-k)\frac{t}{k^n})\right]}^m\\ \le & {\left[\nu (x_0-x_1,(1-k)\frac{t}{k^n})\right]}^{n^p}\to 0,\end{array}$$

where $p>0$ such that $m<n^p$. Hence the sequence $\{x_n\}$ is a Cauchy sequence. This is not correct since the same q (or p) would not be valid for all positive integers $m>n\ge n_0$. For instance, let $(X,\parallel \cdot \parallel )$ be an ordinary normed space, define $\mu (x,t)=\frac{t}{t+\parallel x\parallel }$ for any $x\in X$ and $t>0$ and $a\ast b=ab$ for all $a,b\in [0,1]$. Then $(X,\mu ,1-\mu ,\ast ,{\ast }^{\mathrm{\prime }})$ is an IFNS. If $k=1/2$ and $m=2^n$, we have

$${\left[\mu (x_0-x_1,(1-k)\frac{t}{k^n})\right]}^m={\left[\frac{2^{n-1}t}{2^{n-1}t+\parallel x_0-x_1\parallel }\right]}^{2^n}\to e^{-\frac{2\parallel x_0-x_1\parallel }{t}}<1.$$

Also, the proof lines of Theorem 2.4 that are not correct are the following ones (see p.1902, lines 22-32):

where $q>0$ such that $m<n^q$. In general, we cannot obtain $\mu (x_n-x_m,t)\to 1$ as $n,m\to \mathrm{\infty }$. It is not shown that $\{x_n\}$ is a Cauchy sequence. Moreover, a similar conclusion can be obtained for $\nu (x_n-x_m,t)\to 0$. Thus, from the hypothesis of Theorem 2.4, the conclusion cannot be guaranteed.

4 The modification in FNS

In this section, by replacing the hypothesis that μ satisfies the n-property with the one that the t-norm is of H-type, we state and prove a coupled fixed point theorem as a modification.

Definition 4.1 [13]

For any $a\in [0,1]$, let the sequence ${\{{\ast }^{n}a\}}_{n=1}^{\mathrm{\infty }}$ be defined by ${\ast }^{1}a=a$ and ${\ast }^{n}a=({\ast }^{n-1}a)\ast a$. Then a t-norm ∗ is said to be of H-type if the sequence ${\{{\ast }^{n}a\}}_{n=1}^{\mathrm{\infty }}$ is equicontinuos at $a=1$.

Theorem 4.1 Let $(X,⊑)$ be a partially ordered set and $(X,\mu ,\ast )$ be a complete FNS such that ∗ is of H-type and $a\ast b\ge ab$ for all $a,b\in [0,1]$. Let $k\in (0,1)$ be a number and $F:X\times X\to X$ be a mapping such that F has the mixed monotone property and

$$\mu (F(x,y)-F(u,v),kt)\ge {[\mu (x-u,t)]}^{1/2}\ast {[\mu (y-v,t)]}^{1/2},$$

(4.1)

for which $x⊑u$ and $y⊒v$. Suppose that either

• (a) F is continuous or

• (b) X has the sequential monotone property.

If there exist $x_0,y_0\in X$ such that $x_0⊑F(x_0,y_0)$ and $y_0⊒F(y_0,x_0)$, then F has a coupled fixed point. Furthermore, if $x_0$ and $y_0$ are comparable, then $x=y$, that is, $x=F(x,x)$.

Proof Let $x_0,y_0\in X$ be such that $x_0⊑F(x_0,y_0)$ and $y_0⊒F(y_0,x_0)$. Since $F(X\times X)\subseteq X$, we can choose $x_1,y_1\in X$ such that $x_1=F(x_0,y_0)$ and $y_1=F(y_0,x_0)$. Again, from $F(X\times X)\subseteq X$, we can choose $x_2,y_2\in X$ such that $x_2=F(x_1,y_1)$ and $y_2=F(y_1,x_1)$. Continuing this process, we can construct two sequences $\{x_n\}$ and $\{y_n\}$ in X such that, for each $n\ge 0$,

$$x_{n+1}=F(x_n,y_n),y_{n+1}=F(y_n,x_n).$$

(4.2)

The proof is divided into two steps.

Step 1. Prove that $\{x_n\}$ and $\{y_n\}$ are Cauchy sequences. Firstly, we show by induction that, for each $n\ge 0$,

$$x_n⊑x_{n+1},y_n⊒y_{n+1}.$$

(4.3)

For $n=0$, (4.3) holds trivially. Suppose that, for some fixed $n\ge 0$, (4.3) holds. Since $x_n⊑x_{n+1}$ and $x_n⊒x_{n+1}$ and F has the mixed monotone property, it follows from (4.2) that

$$x_{n+1}=F(x_n,y_n)⊑F(x_{n+1},y_n),y_{n+1}=F(y_n,x_n)⊒F(y_{n+1},x_n).$$

(4.4)

Similarly, we have

$$x_{n+2}=F(x_{n+1},y_{n+1})⊒F(x_{n+1},y_n),y_{n+2}=F(y_{n+1},x_{n+1})⊑F(y_{n+1},x_n).$$

(4.5)

Thus, combining (4.4) and (4.5), (4.3) holds.

Let ${\delta }_n(t)={[\mu (x_n-x_{n+1},t)]}^{1/2}\ast {[\mu (y_n-y_{n+1},t)]}^{1/2}$ for all $n\ge 0$. Then it follows from (4.1), (4.3) and (F3) that

$$\begin{array}{rcl}\mu (x_n-x_{n+1},kt)& =& \mu (F(x_{n-1},y_{n-1})-F(x_n,y_n),kt)\\ \ge & {[\mu (x_{n-1}-x_n,t)]}^{1/2}\ast {[\mu (y_{n-1}-y_n,t)]}^{1/2}\\ =& {\delta }_{n-1}(t)\end{array}$$

(4.6)

and

$$\begin{array}{rcl}\mu (y_n-y_{n+1},kt)& =& \mu (F(y_n,x_n)-F(y_{n-1},x_{n-1}),kt)\\ \ge & {[\mu (y_n-y_{n-1},t)]}^{1/2}\ast {[\mu (x_n-x_{n-1},t)]}^{1/2}\\ =& {\delta }_{n-1}(t).\end{array}$$

(4.7)

Then it follows from the t-norm and $a\ast b\ge ab$ that ${\delta }_n(kt)\ge {\delta }_{n-1}(t)$ for all $n\ge 1$. This implies that

$$1\ge {\delta }_n(t)\ge {\delta }_{n-1}\left(\frac{t}{k}\right)\ge {\delta }_{n-2}\left(\frac{t}{k^2}\right)\ge \cdots \ge {\delta }_0\left(\frac{t}{k^n}\right).$$

(4.8)

Since ${lim}_{n\to \mathrm{\infty }}{\delta }_0(\frac{t}{k^n})=1$ for all $t>0$, we have ${lim}_{n\to \mathrm{\infty }}{\delta }_n(t)=1$ for all $t>0$.

Now, we claim that, for any $p\ge 1$,

$$\mu (x_n-x_{n+p},t)\ge {\ast }^p{\delta }_{n-1}(t-kt),\mu (y_n-y_{n+p},t)\ge {\ast }^p{\delta }_{n-1}(t-kt),\mathrm{\forall }n\ge 1.$$

(4.9)

In fact, it is obvious for $p=1$ by (4.6), (4.7) and Lemma 2.1 since $t/k\ge t-kt$ and ${\delta }_{n-1}^1$ is non-decreasing. Assume that (4.9) holds for some $p\ge 1$. By (4.7), we have

$$\mu (x_n-x_{n+1},t)\ge \mu (x_n-x_{n+1},kt)\ge {\delta }_{n-1}(t)$$

and so

$$\mu (x_n-x_{n+1},t-kt)\ge {\delta }_{n-1}(t-kt).$$

Thus, from (4.1), (4.9) and $a\ast b\ge ab$, we have

$$\mu (x_{n+1}-x_{n+p+1},kt)\ge {[\mu (x_n-x_{n+p},t)]}^{1/2}\ast {[\mu (y_n-y_{n+p},t)]}^{1/2}\ge {\ast }^p{\delta }_{n-1}(t-kt).$$

Hence, by the monotonicity of the t-norm ∗, we have

$$\begin{array}{rcl}\mu (x_n-x_{n+p+1},t)& =& \mu (x_n-x_{n+p+1},t-kt+kt)\\ \ge & \mu (x_n-x_{n+1},t-kt)\ast \mu (x_{n+1}-x_{n+p+1},kt)\\ \ge & {\delta }_{n-1}(t-kt)\ast ({\ast }^p{\delta }_{n-1}(t-kt))={\ast }^{p+1}{\delta }_{n-1}(t-kt).\end{array}$$

Similarly, we have

$$\mu (y_{n+1}-y_{n+p+1},kt)\ge {\ast }^{p+1}{\delta }_{n-1}(t-kt).$$

Therefore, by induction, (4.9) holds for all $p\ge 1$. Suppose that $t>0$ and $ϵ\in (0,1]$ are given. By hypothesis, since ∗ is a t-norm of H-type, there exists $0<\eta <1$ such that ${\ast }^p(a)>1-ϵ$ for all $a\in (1-\eta ,1]$ and $p\ge 1$. Since ${lim}_{n\to \mathrm{\infty }}{\delta }_n(t)=1$, there exists $n_0$ such that ${\delta }_n(t-kt)>1-\eta$ for all $n\ge n_0$. Hence, from (4.9), we get

$$\mu (x_n-x_{n+p},t)>1-ϵ,\mu (y_n-y_{n+p},t)>1-ϵ,\mathrm{\forall }n\ge n_0.$$

Therefore, $\{x_n\}$ and $\{y_n\}$ are Cauchy sequences.

Step 2. We prove that F has a coupled fixed point. Since X is complete, there exist $x,y\in X$ such that ${lim}_{n\to \mathrm{\infty }}{x}_n=x$ and ${lim}_{n\to \mathrm{\infty }}{y}_n=y$. Suppose that the assumption (a) holds. By the continuity of F, we get

$$x=\underset{n\to \mathrm{\infty }}{lim}{x}_{n+1}=\underset{n\to \mathrm{\infty }}{lim}F(x_n,y_n)=F(\underset{n\to \mathrm{\infty }}{lim}{x}_n,\underset{n\to \mathrm{\infty }}{lim}{y}_n)=F(x,y).$$

Similarly, we can show that $F(y,x)=y$.

Suppose now that (b) holds. Since $\{x_n\}$ is a non-decreasing sequence with $x_n\to x$ and $\{y_n\}$ is a non-increasing sequence with $x_y\to y$, from (B1) and (B2), we have $x_n⊑x$ and $y_n⊒y$ for all $n\ge 1$. Then, by (4.1), we obtain

$$\mu (x_{n+1}-F(x,y),kt)\ge \mu (F(x_n,y_n)-F(x,y),kt)\ge {[\mu (x_n-x,t)]}^{1/2}\ast {[\mu (y_n-y,t)]}^{1/2}.$$

Letting $n\to \mathrm{\infty }$, we have ${lim}_{n\to \mathrm{\infty }}{x}_n=F(x,y)$. Hence $F(x,y)=x$.

Similarly, we can show that $F(y,x)=y$.

Suppose that $x_0⊑y_0$. By induction and the mixed monotone property of F, it follows that $x_n=F(x_{n-1},y_{n-1})⊑F(y_{n-1},x_{n-1})=y_n$. From (4.1), it follows that

$$\begin{array}{rcl}\mu (x_{n+1}-y_{n+1},kt)& =& \mu (F(x_n,y_n)-F(y_n,x_n,kt)\\ \ge & {[\mu (x_n-y_n,t)]}^{1/2}\ast {[\mu (y_n-x_n,t)]}^{1/2}\\ =& \mu (x_n-y_n,t).\end{array}$$

By the iterative procedure, we have

$$\mu (x_n-y_n,kt)\ge \mu (x_{n-1}-y_{n-1},t)\ge \mu (x_{n-2}-y_{n-2},\frac{t}{k})\ge \cdots \ge \mu (x_0-y_0,\frac{t}{k^{n-1}}).$$

Taking $n\to \mathrm{\infty }$, since ${lim}_{n\to \mathrm{\infty }}\mu (x_0-y_0,\frac{t}{k^{n-1}})=1$ for all $t>0$, we conclude that $\mu (x-y,t)\ge 1$ for all $t>0$, i.e., $x=y$. This completes the proof. □

Next, we prove the existence of a coupled coincidence point theorem, where we do not require that F and g are commuting.

Theorem 4.2 Let $(X,⊑)$ be a partially ordered set and let $(X,\mu ,\ast )$ be a complete FNS such that ∗ is of H-type and $a\ast b\ge ab$ for all $a,b\in [0,1]$. Let $k\in (0,1)$ be a number and $F:X\times X\to X$ and $g:X\to X$ be two mappings such that F has the mixed g-monotone property and

$$\mu (F(x,y)-F(u,v),kt)\ge {[\mu (gx-gu,t)]}^{1/2}\ast {[\mu (gy-gv,t)]}^{1/2},$$

(4.10)

for which $gx⊑gu$ and $gy⊒gv$. Suppose that $F(X\times X)\subseteq g(X)$, g is continuous and either

• (a) F is continuous or

• (b) X has the sequential g-monotone property.

If there exist $x_0,y_0\in X$ such that $g{x}_0⊑F(x_0,y_0)$ and $g{y}_0⊒F(y_0,x_0)$, then there exist $x,y\in X$ such that $gx=F(x,y)$ and $gy=F(y,x)$, that is, F and g have a coupled coincidence point.

Proof Using Lemma 2.2, there exists $E\subset X$ such that $g(E)=g(X)$ and $g:E\to X$ is one-to-one. We define a mapping $\mathcal{A}:g(E)\times g(E)\to X$ by $\mathcal{A}(gx,gy)=F(x,y)$. Since g is one-to-one on $g(E)$, $\mathcal{A}$ is well defined. Thus it follows from (4.10) that

$$\mu (\mathcal{A}(gx,gy)-\mathcal{A}(gu,gv),kt)\ge {[\mu (gx-gu,t)]}^{1/2}\ast {[\mu (gy-gv,t)]}^{1/2},$$

(4.11)

for which $gx⊑gu$ and $gy⊒gv$. Since F has the mixed g-monotone property, we have

which implies that $\mathcal{A}$ has the mixed monotone property.

Suppose that the assumption (a) or (b) holds. Using Theorem 4.1 with the mapping $\mathcal{A}$, it follows that $\mathcal{A}$ has a coupled fixed point $(u,v)\in g(X)\times g(X)$, i.e., $u=\mathcal{A}(u,v)$ and $v=\mathcal{A}(v,u)$. Since $(u,v)\in g(X)\times g(X)$, there exists $(\tilde{u},\tilde{v})\in X\times X$ such that $g\tilde{u}=u$ and $g\tilde{v}=v$. Thus $g\tilde{u}=u=\mathcal{A}(u,v)=\mathcal{A}(g\tilde{u},g\tilde{v})$. Similarly, $g\tilde{v}=\mathcal{A}(g\tilde{v},g\tilde{u})$. This completes the proof. □

Now, we show the existence and uniqueness of coupled coincidence points. Note that if $(S,⊑)$ is a partially ordered set, then we endow the product $S\times S$ with the following partial order:

$$(x,y)⊑(u,v)⟺x⊑u,y⊒v,\mathrm{\forall }x,y,u,v\in S.$$

We say that $(x,y)$ and $(u,v)$ are comparable if $(x,y)⊑(u,v)$ or $(x,y)⊒(u,v)$.

Theorem 4.3 In addition to the hypotheses of Theorem  4.2, suppose that, for any pair of coupled coincidence points $(x,y),(x^{\ast },y^{\ast })\in X\times X$, there exists a point $(u,v)\in X\times X$ such that $(gu,gv)$ is comparable to $(gx,gy)$ and $(g{x}^{\ast },g{y}^{\ast })$. Then F and g have a unique coupled coincidence point, that is, there exists a unique $(x,y)\in X\times X$ such that $x=gx=F(x,y)$ and $y=gy=F(y,x)$.

Proof From Theorem 4.2, the set of coupled coincidences is nonempty. Now, we show that if $(x,y)$ and $(x^{\ast },y^{\ast })$ are coupled coincidence points, that is, $gx=F(x,y)$, $gy=F(y,x)$ and $g{x}^{\ast }=F(x^{\ast },y^{\ast })$, $g{y}^{\ast }=F(y^{\ast },x^{\ast })$, then

$$gx=g{x}^{\ast },gy=g{y}^{\ast }.$$

(4.12)

Put $u_0=u$ and $v_0=v$ and choose $u_1,v_1\in X$ such that $g{u}_1=F(u_0,v_0)$ and $g{v}_1=F(v_0,u_0)$. Then, as in the proof of Theorem 4.2, we can inductively define the sequences $\{u_n\}$ and $\{v_n\}$ such that

$$g{u}_{n+1}=F(u_n,v_n),g{v}_{n+1}=F(v_n,u_n).$$

(4.13)

Since $(F(x,y),F(y,x))=(gx,gy)$ and $(F(u,v),F(v,u))=(g{u}_1,g{v}_1)$ are comparable, we can suppose that $gx⊑g{u}_1$ and $gy⊒g{v}_1$. It is easy to show, by induction and g-monotonicity, that $gx⊑g{u}_n$ and $gy⊒g{v}_n$ for all $n\ge 1$. From (4.1), we obtain

$$\begin{array}{rcl}\mu (gx-g{u}_n,kt)& =& \mu (F(x,y)-F(u_{n-1},v_{n-1}),kt)\\ \ge & {[\mu (gx-g{u}_{n-1},t)]}^{1/2}\ast {[\mu (gy-g{v}_{n-1},t)]}^{1/2}\end{array}$$

(4.14)

and

$$\begin{array}{rcl}\mu (g{v}_n-gy,kt)& =& \mu (F(v_{n-1},u_{n-1})-F(y,x),kt)\\ \ge & {[\mu (g{v}_{n-1}-gy,t)]}^{1/2}\ast {[\mu (g{u}_{n-1}-gx,t)]}^{1/2}.\end{array}$$

(4.15)

Now, let ${\beta }_n(t)={[\mu (gx-g{u}_n,t)]}^{1/2}\ast {[\mu (gy-g{v}_n,t)]}^{1/2}$. By (4.14) and (4.15), we have

$${\beta }_n(t)\ge {\beta }_{n-1}\left(\frac{t}{k}\right)\ge \cdots \ge {\beta }_0\left(\frac{t}{k^n}\right)$$

and

$$\mu (gx-g{u}_n,kt)\ge {\beta }_0\left(\frac{t}{k^n}\right),\mu (gy-g{v}_n,kt)\ge {\beta }_0\left(\frac{t}{k^n}\right).$$

Since ${lim}_{n\to \mathrm{\infty }}{\beta }_0(\frac{t}{k^n})=1$, we conclude that ${lim}_{n\to \mathrm{\infty }}g{u}_n=gx$ and ${lim}_{n\to \mathrm{\infty }}g{v}_n=gy$.

Similarly, ${lim}_{n\to \mathrm{\infty }}g{u}_n=g{x}^{\ast }$ and ${lim}_{n\to \mathrm{\infty }}g{v}_n=g{y}^{\ast }$. Hence $gx=g{x}^{\ast }$ and $gy=g{y}^{\ast }$ and so (4.12) is proved.

Since $gx=F(x,y)$ and $gy=F(y,x)$, if $z=gx$ and $w=gy$, by the commutativity of F and g, we have

$$gz=ggx=gF(x,y)=F(gx,gy)=F(z,w)$$

and

$$gw=ggy=gF(y,x)=F(gy,gx)=F(w,z),$$

i.e., $(z,w)$ is a coupled coincidence point. In particular, from (4.12), we have $z=gx=gz$ and $w=gy=gw$. Therefore, $(z,w)$ is a coupled common fixed point of F and g.

To prove the uniqueness of the coupled common fixed point of F and g, assume that $(p,q)$ is another coupled common fixed point. Then, by (4.12), we have $p=gp=gz=z$ and $q=gq=gw=w$. This completes the proof. □

Finally, we present an intuitionistic version of Theorem 4.2 with the dual conditions on t-conorms. The proof is just reduced to apply Theorem 4.2 to the support FNS.

Corollary 4.4 Let $(X,⊑)$ be a partially ordered set and suppose that $a\ast b\ge ab$ and $(1-a)\diamond (1-b)\le 1-ab$ for all $a,b\in [0,1]$. Let $(X,\mu ,\nu ,\ast ,\diamond )$ be a complete IFNS such that ∗ and ⋄ are of H-type. Let $F:X\times X\to X$ and $g:X\to X$ be two mappings such that F has the mixed g-monotone property,

$$\mu (F(x,y)-F(u,v),kt)\ge {[\mu (gx-gu,t)]}^{1/2}\ast {[\mu (gy-gv,t)]}^{1/2}$$

and

(4.16)

for which $g(x)⊑g(u)$ and $g(y)⊒g(v)$, where $0<k<1$, $F(X\times X)\subseteq g(X)$ and g is continuous. Suppose that either

• (a) F is continuous or

• (b) X has the sequential g-monotone property.

If there exist $x_0,y_0\in X$ such that $g(x_0)⊑F(x_0,y_0)$ and $g(y_0)⊒F(y_0,x_0)$, then there exist $x,y\in X$ such that $g(x)=F(x,y)$ and $g(y)=F(y,x)$, that is, F and g have a coupled coincidence point.