- Research
- Open access
- Published:
Generalized weyl's theorem for algebraically quasi-paranormal operators
Journal of Inequalities and Applications volume 2012, Article number: 89 (2012)
Abstract
Let T or T* be an algebraically quasi-paranormal operator acting on a Hilbert space. We prove: (i) generalized Weyl's theorem holds for f(T) for every f ∈ H(σ (T)); (ii) generalized a-Browder's theorem holds for f(S) for every S ≺ T and f ∈ H(σ(S)); (iii) the spectral mapping theorem holds for the B-Weyl spectrum of T. Moreover, we show that if T is an algebraically quasi-paranormal operator, then T + F satisfies generalized Weyl's theorem for every algebraic operator F which commutes with T.
Mathematics Subject Classification (2010): Primary 47A10, 47A53; Secondary 47B20.
1. Introduction
Throughout this article, we assume that  is an infinite dimensional separable Hilbert space. Let and denote, respectively, the algebra of bounded linear operators and the ideal of compact operators acting on
is an infinite dimensional separable Hilbert space. Let and denote, respectively, the algebra of bounded linear operators and the ideal of compact operators acting on  . If we shall write N(T) and R(T) for the null space and range of T. Also, let α(T): = dimN(T), β(T): = dimN(T*), and let σ(T), σ
a
(T), σ
p
(T), π(T), E(T) denote the spectrum, approximate point spectrum, point spectrum of T, the set of poles of the resolvent of T, the set of all eigenvalues of T which are isolated in σ(T), respectively. An operator is called upper semi-Fredholm if it has closed range and finite dimensional null space and is called lower semi-Fredholm if it has closed range and its range has finite co-dimension. If is either upper or lower semi-Fredholm, then T is called semi-Fredholm, and index of a semi-Fredholm operator is defined by
. If we shall write N(T) and R(T) for the null space and range of T. Also, let α(T): = dimN(T), β(T): = dimN(T*), and let σ(T), σ
a
(T), σ
p
(T), π(T), E(T) denote the spectrum, approximate point spectrum, point spectrum of T, the set of poles of the resolvent of T, the set of all eigenvalues of T which are isolated in σ(T), respectively. An operator is called upper semi-Fredholm if it has closed range and finite dimensional null space and is called lower semi-Fredholm if it has closed range and its range has finite co-dimension. If is either upper or lower semi-Fredholm, then T is called semi-Fredholm, and index of a semi-Fredholm operator is defined by
If both α(T) and β(T) are finite, then T is called Fredholm. is called Weyl if it is Fredholm of index zero. For and a nonnegative integer n define T
n
to be the restriction of T to R(Tn) viewed as a map from R(Tn ) into R(Tn ) (in particular T0 = T). If for some integer n the range R(Tn ) is closed and T
n
is upper (resp. lower) semi-Fredholm, then T is called upper (resp. lower) semi-B-Fredholm. Moreover, if T
n
is Fredholm, then T is called B-Fredholm. T is called semi-B-Fredholm if it is upper or lower semi-B-Fredholm. Let T be semi-B-Fredholm and let d be the degree of stable iteration of T. It follows from [1, Proposition 2.1] that T
m
is semi-Fredholm and i(T
m
) = i(T
d
) for each m ≥ d. This enables us to define the index of semi-B-Fredholm T as the index of semi-Fredholm T
d
. Let be the class of all B-Fredholm operators. In [2], they studied this class of operators and they proved [2, Theorem 2.7] that an operator is B-Fredholm if and only if T = T1 ⊕ T2, where T1 is Fredholm and T2 is nilpotent. It appears that the concept of Drazin invertibility plays an important role for the class of B-Fredholm operators. Let  be a unital algebra. We say that an element is Drazin invertible of degree k if there exists an element such that
be a unital algebra. We say that an element is Drazin invertible of degree k if there exists an element such that
Let . Then the Drazin spectrum is defined by
For , the smallest nonnegative integer p such that N (Tp ) = N(Tp+1) is called the ascent of T and denoted by p(T). If no such integer exists, we set p(T) = ∞. The smallest nonnegative integer q such that R(Tq ) = R(Tq+1) is called the descent of T and denoted by q(T). If no such integer exists, we set q(T) = ∞. It is well known that T is Drazin invertible if and only if it has finite ascent and descent, which is also equivalent to the fact that
An operator is called B-Weyl if it is B-Fredholm of index 0. The B-Fredholm spectrum σ BF (T) and B-Weyl spectrum σ BW (T) of T are defined by
Now, we consider the following sets:
By definition,
is the upper semi-B-essential approximate point spectrum and
is the left Drazin spectrum. It is well known that
where we write acc K for the accumulation points of . If we write iso K: = K \ acc K then we let
We say that an operator T has the single valued extension property at λ (abbreviated SVEP at λ) if for every open set U containing λ the only analytic function which satisfies the equation
is the constant function f ≡ 0 on U. T has SVEP if T has SVEP at every point .
Definition 1.1. Let .
-
(1)
Generalized Weyl's theorem holds for T (in symbols, ) if
-
(2)
Generalized Browder's theorem holds for T (in symbols, ) if
-
(3)
Generalized a-Weyl's theorem holds for T (in symbols, ) if
-
(4)
Generalized a-Browder's theorem holds for T (in symbols, ) if
It is known ([3]) that the following set inclusions hold:
Recently, Han and Na introduced a new operator class which contains the classes of paranormal operators and quasi-class A operators [4]. In [5], it was shown that generalized Weyl's theorem holds for algebraically paranormal operators. In this article, we extend this result to algebraically quasi-paranormal operators using the local spectral theory
2. Generalized Weyl's theorem for algebraically quasi-paranormal operators
Definition 2.1. (1) An operator is said to be class A if
-
(2)
T is called a quasi-class A operator if
-
(3)
An operator is said to be paranormal if
Recently, we introduced a new operator class which is a common generalization of paranormal operators and quasi-class A operators [4].
Definition 2.2. An operator is called quasi-paranormal if
We say that is an algebraically quasi-paranormal operator if there exists a non-constant complex polynomial h such that h(T) is quasi-paranormal.
In general, the following implications hold:
class A ⇒ quasi-class A ⇒ quasi-paranormal;
paranormal ⇒ quasi-paranormal ⇒ algebraically quasi-paranormal.
In [4], it was observed that there are examples which are quasi-paranormal but not paranormal, as well as quasi-paranormal but not quasi-class A. We give a more simple example which is quasi-paranormal but not quasi-class A. To construct this example we recall the following lemma in [4].
Lemma 2.3. An operator is quasi-paranormal if and only if
Example 2.4. . Then it is quasi-paranormal but not quasi-class
A.
Proof. Since
Therefore
On the other hand, since
. Hence T is not quasi-class A.
However, since
we have
for all λ > 0. Therefore T is quasi-paranormal. □
The following example provides an operator which is algebraically quasi-paranormal but not quasi-paranormal.
Example 2.5 Let . Then it is algebraically quasi-paranormal but not quasi-paranormal.
Proof. Since , we have
Therefore
Since (2λ2 - 10λ + 10)I is not a positive operator for λ = 2, for λ > 0. Therefore T is not quasi-paranormal. On the other hand, consider the complex polynomial h(z) = (z - 1)2. Then h(T) = 0, and hence T is algebraically quasi-paranormal.
□
The following facts follow from the above definition and some well known facts about quasi-paranormal operators [4]:
-
(i)
If is algebraically quasi-paranormal, then so is T-λ for each .
-
(ii)
If is algebraically quasi-paranormal and
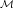 is a closed T-invariant subspace
is a closed T-invariant subspace
of  , then is algebraically quasi-paranormal.
, then is algebraically quasi-paranormal.
-
(iii)
If T is algebraically quasi-paranormal, then T has SVEP.
-
(iv)
Suppose T does not have dense range. Then we have:
T is quasi-paranormal on ,
where is paranormal.
An operator is called isoloid if iso σ(T) ⊆ σ p (T) and an operator is called polaroid if iso σ(T) ⊆ π(T).
In general, the following implications hold:
However, each converse is not true. Consider the following example: let be defined by
Then T is a compact quasinilpotent operator with α(T) = 1, and so T is isoloid. However, since q(T) = ∞, T is not polaroid.
An important subspace in local spectral theory is the quasi-nilpotent part of T defined by
If , then the analytic core K(T) is the set of all such that there exists a constant c > 0 and a sequence of elements such that x0 = x, Tx n = x n -1, and ║x n ║≤ cn║x║ for all , see [6] for information on K(T).
Let denotes the class of all operators for which there exists for which
and denotes the class of all operators for which there exists for which
Evidently, . Now we give a characterization of .
Theorem 2.6. if and only if π(T) = E(T).
Proof. Suppose and let λ ∈ E(T). Then there exists such that H0(T- λ) = N(T - λ)p. Since λ is an isolated point of σ(T), it follows from [6, Theorem 3.74] that
Therefore, we have
and hence , which implies, by [6, Theorem 3.6], that p(T - λ) = q(T - λ) ≤ p. But α(T - λ) > 0, hence λ ∈ π(T). Therefore E(T) ⊆ π(T). Since the opposite inclusion holds for every operator T, we then conclude that π(T) = E(T). Conversely, suppose π(T) = E(T). Let λ ∈ E(T). Then p : = p(T - λ) = q(T - λ) < ∞. By [6, Theorem 3.74], H0(T - λ) = N(T - λ)p. Therefore . □
From Theorem 2.6, we can give a simple example which belongs to but not . Let U be the unilateral shift on and let T = U*. Then T does not have SVEP at 0, and so H0(T) is not closed. Therefore . However, since , where  is an open unit disk in
is an open unit disk in  . Hence by Theorem 2.6.
. Hence by Theorem 2.6.
Before we state our main theorem (Theorem 2.9) in this section, we need some preliminary results.
Lemma 2.7. Let be a quasinilpotent algebraically quasi-paranormal operator. Then T is nilpotent.
Proof. We first assume that T is quasi-paranormal. We consider two cases:
Case I: Suppose T has dense range. Then clearly, it is paranormal. Therefore T is nilpotent by [7, Lemma 2.2].
Case II: Suppose T does not have dense range. Then we can represent T as the upper triangular matrix
where is an paranormal operator. Since T is quasinilpotent, σ(T) = {0}. But σ(T) = σ(A) ∪ {0}, hence σ(A) = {0}. Since A is paranormal, A = 0 and therefore T is nilpotent. Thus if T is a quasinilpotent quasi-paranormal operator, then it is nilpotent. Now, we suppose T is algebraically quasi-paranormal. Then there exists a nonconstant polynomial p such that p(T) is quasi-paranormal. If p(T) has dense range, then p(T) is paranormal. So T is algebraically paranormal, and hence T is nilpotent by [7, Lemma 2.2]. If p(T) does not have dense range, we can represent p(T) as the upper triangular matrix
where is paranormal. Since T is quasinilpotent, σ(p(T)) = p(σ(T)) = {p(0)}. But σ(p(T)) = σ(C)∪{0} by [8, Corollary 8], hence σ(C)∪{0} = {p(0)}. So p(0) = 0, and hence p(T) is quasinilpotent. Since p(T) is quasi-paranormal, by the previous argument p(T) is nilpotent. On the other hand, since p(0) = 0, p(z) = czm (z - λ1)(z - λ2) ... (z - λ n ) for some natural number m. Therefore p(T) = cTm (T - λ1)(T - λ2) ... (T - λ n ). Since p(T) is nilpotent and T - λ i is invertible for every λ i ≠ 0, T is nilpotent. This completes the proof. □
Theorem 2.8. Let be algebraically quasi-paranormal. Then .
Proof. Suppose T is algebraically quasi-paranormal. Then h(T) is a quasi-paranormal operator for some nonconstant complex polynomial h. Let λ ∈ E(T). Then λ is an isolated point of σ(T) and α(T - λ) > 0. Using the spectral projection , where D is a closed disk of center λ which contains no other points of σ(T), we can represent T as the direct sum
Since T1 is algebraically quasi-paranormal, so is T1 - λ. But σ(T1 - λ) = {0}, it follows from Lemma 2.7 that T1 - λ is nilpotent. Therefore T1 - λ has finite ascent and descent. On the other hand, since T2 - λ is invertible, clearly it has finite ascent and descent. Therefore λ is a pole of the resolvent of T, and hence λ ∈ π(T). Hence E(T) ⊆ π(T). Since π(T) ⊆ E(T) holds for any operator T, we have π(T) = E(T). It follows from Theorem 2.6 that . □
We now show that generalized Weyl's theorem holds for algebraically quasi-paranormal operators. In the following theorem, recall that H(σ(T)) is the space of functions analytic in an open neighborhood of σ(T).
Theorem 2.9. Suppose that T or T* is an algebraically quasi-paranormal operator. Then for each f ∈ H(σ(T)).
Proof. Suppose T is algebraically quasi-paranormal. We first show that . Suppose that λ ∈ σ(T)\σ BW (T). Then T - λ is B-Weyl but not invertible. It follows from [9, Lemma 4.1] that we can represent T - λ as the direct sum
Since T is algebraically quasi-paranormal, it has SVEP. So T1 and T2 have both finite ascent. But T1 is Weyl, hence T1 has finite descent. Therefore T-λ has finite ascent and descent, and so λ ∈ E(T). Conversely, suppose that λ ∈ E(T). Since T is algebraically quasi-paranormal, it follows from Theorem 2.8 that . Since π(T) = E(T) by Theorem 2.6, λ ∈ E(T). Therefore T - λ has finite ascent and descent, and so we can represent T - λ as the direct sum
Therefore T - λ is B-Weyl, and so λ ∈ σ(T) \ σ BW (T). Thus σ(T) \ σ BW (T) = E(T), and hence .
Next, we claim that σ BW (f(T)) = f(σ BW (T)) for each f ∈ H(σ(T)). Since . It follows from [5, Theorem 2.1] that σ BW (T) = σ D (T). Since T is algebraically quasi-paranormal, f(T) has SVEP for each f ∈ H(σ(T)). Hence by [5, Theorem 2.9], and so σ BW (f(T)) = σ D (f(T)). Therefore we have
Since T is algebraically quasi-paranormal, it follows from the proof of Theorem 2.8 that it is isoloid. Hence for any f ∈ H(σ(T)) we have
Since , we have
which implies that .
Now suppose that T* is algebraically quasi-paranormal. We first show that . Let λ ∈ σ(T) \ σ BW (T). Observe that and . So , and so because . Since T* is algebraically quasi-paranormal, it follows from Theorem 2.8 that . Hence T - λ has finite ascent and descent, and so λ ∈ E(T). Conversely, suppose λ ∈ E(T). Then λ is an isolated point of σ(T) and α(T - λ) > 0. Since is an isolated point of σ(T*). Since T* is isoloid, . But E(T*) = π(T*) by Theorem 2.8, hence we have T - λ has finite ascent and descent. Therefore we can represent T - λ as the direct sum
Therefore T - λ is B-Weyl, and so λ ∈ σ(T) \ σ BW (T). Thus σ(T) \ σ BW (T) = E(T), and hence . If T* is algebraically quasi-paranormal then T is isoloid. It follows from the first part of the proof that . This completes the proof. □
From the proof of Theorem 2.9 and [10, Theorem 3.4], we obtain the following useful consequence.
Corollary 2.10. Suppose T or T* is algebraically quasi-paranormal. Then
An operator is called a quasiaffinity if it has trivial kernel and dense range. is said to be a quasiaffine transform of (notation: S ≺ T) if there is a quasiaffinity such that XS = TX. If both S ≺ T and T ≺ S, then we say that S and T are quasisimilar.
Corollary 2.11. Suppose T is algebraically quasi-paranormal and S ≺ T. Then for each f ∈ H(σ(S)).
Proof. Suppose T is algebraically quasi-paranormal. Then T has SVEP. Since S ≺ T, f(S) has SVEP by [7, Lemma 3.1]. It follows from [11, Theorem 3.3.6] that f(S) has SVEP. Therefore by [12, Corollary 2.5]. □
3. Generalized Weyl's theorem for perturbations of algebraically quasi-paranormal operators
An operator T is said to be algebraic if there exists a nontrivial polynomial h such that h(T) = 0. From the spectral mapping theorem it easily follows that the spectrum of an algebraic operator is a finite set. It is known that generalized Weyl's theorem is not generally transmitted to perturbation of operators satisfying generalized Weyl's theorem. In [13], they proved that if T is paranormal and F is an algebraic operator commuting with T, then Weyl's theorem holds for T + F. We now extend this result to generalized Weyl's theorem for algebraically quasi-paranormal operators. We begin with the following lemma.
Lemma 3.1. Let . Then the following statements are equivalent:
-
(1)
;
-
(2)
T has SVEP at every and π(T) = E(T).
Proof. Observe that if and only if σ BW (T) = σ D (T). So if and only if T has SVEP at every . Therefore we obtain the desired conclusion. □
From this lemma, we obtain the following corollary
Corollary 3.2. Let . Suppose T has SVEP. Then
Proof. Since T has SVEP, by Lemma 3.1. So σ(T) \ σ BW (T) = π(T). Therefore if and only if by Theorem 2.6. □
Lemma 3.3. Suppose and N is nilpotent such that TN = NT. Then if and only if .
Proof. Suppose Np = 0 for some . Observe that without any assumption on T we have
Suppose now that , or equivalently π(T) = E(T). We show first E(T) = E(T+N). Let λ ∈ E(T). Without loss of generality, we may assume that λ = 0. From σ(T+N) = σ(T), we see that 0 is an isolated point of σ(T+N). Since 0 ∈ E(T), α(T) > 0 and hence by the first inclusion in (3.3.1) we have α(T+N)p> 0. Therefore α(T+N) > 0, and hence 0 ∈ E(T+N). Thus the inclusion E(T) ⊆ E(T + N) is proved. To show the opposite inclusion, assume that 0 ∈ E(T + N). Then 0 is an isolated point of σ(T) because σ(T + N) = σ(T). Since α(T + N) > 0, the second inclusion in (3.3.1) entails that α(Tp ) > 0. Therefore α(T) > 0, and hence 0 ∈ E(T). So the equality E(T) = E(T + N) is proved. Suppose . Then π(T) = E(T) by Theorem 2.6, and so π(T + N) = π(T) = E(T) = E(T + N). Therefore . Conversely, if by symmetry we have π(T) = π(T + N) = E(T + N) = E((T + N)-N) = E(T), so the proof is complete. □
The following theorem is a generalization of [13, Theorem 2.5]. The proof of the following theorem is strongly inspired to that of it.
Theorem 3.4. Suppose T is algebraically quasi-paranormal. If F is algebraic with TF = FT, then .
Proof. Since F is algebraic, σ(F) is finite. Let σ(F) = {μ1,μ2,...,μ n }. Denote by P i the spectral projection associated with F and the spectral set {μ i }. Let Y i : = R(P i ) and Z i : = N(P i ). Then H = Y i ⊕ Z i and the closed subspaces Y i and Z i are invariant under T and F. Moreover, σ(F|Y i ) = {μ i }. Define F i : = F|Y i and Ti : = T|Y i . Then clearly, the restrictions T i and F i commute for every i = 1, 2,...,n and
Let h be a nontrivial complex polynomial such that h(F) = 0. Then h(F i ) = h(F|Y i ) = h(F)|Y i = 0, and from {0} = σ(h(F i )) = h(σ(F i )) = h({μ i }), we obtain that h(μ i ) = 0. Write h(μ) = (μ - μ i )mg(μ) with g(μ i ) = 0. Then 0 = h(F i ) = (F - μ i )mg(F i ), where g(F i ) is invertible. Hence N i : = F i - μ i are nilpotent for all i = 1, 2,...,n. Observe that
Since T i + μ i is algebraically quasi-paranormal for all i = 1, 2,...,n, T i + μ i has SVEP. Moreover, since N i is nilpotent with T i N i = N i T i , it follows from [6, Corollary 2.12] that T i + N i + μ i has SVEP, and hence T i + F i has SVEP. From [6, Theorem 2.9] we obtain that
Now, we show that . Since T i + μ i is algebraically quasi-paranormal, by Theorem 2.8. By Lemma 3.3 and (3.4.1), for every i = 1, 2,...,n. Now assume that λ0 ∈ E(T + F). Fix such that 1 ≤ i ≤ n. Since the equality T i + N i - λ0 + μ i = T i + F i - λ0 holds, we consider two cases:
Case I: Suppose that T i - λ0 + μ i is invertible. Since N i is quasi-nilpotent commuting with T i - λ0 + μ i , it is clear that T i + F i - λ0 is also invertible. Hence H0(T i + F i - λ0) = N(T i + F i - λ0) = {0}.
Case II: Suppose that T i - λ0 + μ i is not invertible. Then λ0 - μ i ∈ σ(T i ). We claim that λ0 ∈ E(T i + F i ). Note that λ0 ∈ σ(T i + μ i ) = σ(T i + F i ). Since σ(T i + F i ) ∈ σ(T + F) and λ0 ∈ iso σ(T + F), λ0 ∈ iso σ(T i + N i + μ i ). Therefore λ0 -μ i ∈ iso σ(T i + N i ) = iso σ(T i ). Since T i - λ0 + μ i is algebraically quasi-paranormal, λ0 - μ i ∈ π(T i ). Since π(T i ) = E(T i ) by Theorem 2.6 and by Theorem 2.9, λ0 - μ i ∈ E(T i ) = σ(T i ) \ σ BW (T i ). But N i is nilpotent with T i N i = N i T i , hence σ D (T i ) = σ D (T i + N i ) and . Therefore we have σ BW (T i + N i ) = σ D (T i + N i ). Hence
Hence T i + F i - λ0 is B-Weyl. Assume to the contrary that T i + F i - λ0 is injective. Then β(T i + F i - λ0) = α(T i + F i - λ0) = 0. Therefore T i + F i - λ0 is invertible, and so λ0 ∉ σ(T i +F i ). This is a contradiction. Hence λ0 ∈ E(T i + F i ). Since by Theorem 2.6, there exists a positive integer m i such that H 0 (T i + F i - λ0) = N(T i + F i - λ0) mi .
From Cases I and II we have
where m : = max{m1,m2,...,m n }. Since the last equality holds for every λ0 ∈ E(T + F), . Therefore by Corollary 3.2. □
It is well known that if for an operator there exists a natural number n for which Fn is finite-dimensional, then F is algebraic.
Corollary 3.5. Suppose is algebraically quasi-paranormal and F is an operator commuting with T such that Fn is a finite-dimensional operator for some . Then .
References
Berkani M, Sarih M: On semi B-Fredholm operators. Glasgow Math J 2001, 43: 457–465.
Berkani M: On a class of quasi-Fredholm operators. Int Equ Oper Theory 1999, 34: 244–249. 10.1007/BF01236475
Berkani M, Koliha JJ: Weyl type theorems for bounded linear operators. Acta Sci Math (Szeged) 2003, 69: 359–376.
Han YM, Na WH: A note on quasi-paranormal operator. Mediterr J Math, in press.
Curto RE, Han YM: Generalized Browder's and Weyl's theorems for Banach space operators. J Math Anal Appl 2007, 336: 1424–1442. 10.1016/j.jmaa.2007.03.060
Aiena P: Fredholm and Local Spectral Theory, with Applications to Multipliers. Kluwer Academic Publishers, Dordrecht; 2004.
Curto RE, Han YM: Weyl's theorem holds for algebraically paranormal operators. Int Equ Oper Theory 2003, 47: 307–314. 10.1007/s00020-002-1164-1
Han JK, Lee HY, Lee WY, et al.: Invertible completions of 2 × 2 upper triangular operator matrices. Proc Am Math Soc 2000, 128: 119–123. 10.1090/S0002-9939-99-04965-5
Berkani M: Index of B -Fredholm operators and generalization of a Weyl theorem. Proc Am Math Soc 2002, 130: 1717–1723. 10.1090/S0002-9939-01-06291-8
Aiena P, Garcia O: Generalized Browder's theorem and SVEP. Mediterr J Math 2007, 4: 215–228. 10.1007/s00009-007-0113-2
Laursen KB, Neumann MM: An Introduction to Local Spectral Theory. London Mathematical Society Monographs New Series 20, Clarendon Press, Oxford; 2000.
Aiena P, Miller TL: On generalized a -Browder's theorem. Studia Math 2007, 180: 285–300. 10.4064/sm180-3-7
Aiena P, Guillen JR: Weyl's theorem for perturbations of paranormal operators. Proc Am Math Soc 2007, 135: 2443–2451. 10.1090/S0002-9939-07-08582-6
Acknowledgements
The authors would like to express their thanks to the referee for several extremely valuable suggestions concerning the article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All authors contributed equally to the writing of the present article. And they also read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
An, I.J., Han, Y.M. Generalized weyl's theorem for algebraically quasi-paranormal operators. J Inequal Appl 2012, 89 (2012). https://doi.org/10.1186/1029-242X-2012-89
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-89
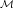 is a closed T-invariant subspace
is a closed T-invariant subspace