- Research
- Open access
- Published:
Some new fractional q-integral Grüss-type inequalities and other inequalities
Journal of Inequalities and Applications volume 2012, Article number: 299 (2012)
Abstract
In this paper, we employ a fractional q-integral on the specific time scale, , where and , to establish some new fractional q-integral Grüss-type inequalities by using one or two fractional parameters. Furthermore, other fractional q-integral inequalities are also obtained.
MSC:26D10, 26A33.
1 Introduction
In the past several years, by using the Riemann-Liouville fractional integrals, the fractional integral inequalities and applications have been addressed extensively by several researchers. For example, we refer the reader to [1–6] and the references cited therein. Dahmani et al. [7] gave the following fractional integral inequalities by using the Riemann-Liouville fractional integrals. Let f and g be two integrable functions on satisfying the following conditions:
For all , and , then
and

To the best of authors’ knowledge, only some fractional q-integral inequalities have been established in recent years. That is, only Öğünmez and Özkan [8], Bohner and Ferreira [9] and Yang [10] obtained some fractional q-integral inequalities. With motivation from the papers [7, 11, 12], the main purpose of this article is to establish some new fractional q-integral inequalities. First of all, by using one or two fractional parameters, we establish some new fractional q-integral Grüss-type inequalities on the specific time scale , where and . In general, a time scale is an arbitrary nonempty closed subset of real numbers [13]. Furthermore, other fractional q-integral inequalities are also obtained.
2 Description of fractional q-calculus
In this section, we introduce the basic definitions on fractional q-calculus. More results concerning fractional q-calculus can be found in [14–17].
Let and define , . For a function , the nabla q-derivative of f
for all . The q-integral of f is
The q-factorial function is defined in the following way: if n is a positive integer, then
If n is not a positive integer, then
The q-derivative of the q-factorial function with respect to t is
and the q-derivative of the q-factorial function with respect to s is
The q-exponential function is defined as
Define the q-gamma function by
Note that
where . The fractional q-integral is defined as
Note that
3 Fractional q-integral Grüss-type inequalities
To state the main results in this paper, we employ the following lemmas. For the sake of convenience, we use the following assumption (A) in this section:
Lemma 1 Let and f be a function defined on . Then, for all and , we have
Proof Let and f be a function defined on . For any and , we have

Multiplying both sides of (2) by and integrating the resulting identity with respect to τ from 0 to t, we get

Multiplying both sides of (3) by and integrating the resulting identity with respect to ρ from 0 to t, we obtain

which implies (1). □
Lemma 2 Let f and g be two functions defined on . Then, for all , and , we have

Proof In order to prove Lemma 2, we firstly prove that the following inequality (i.e., Cauchy-Schwarz inequality for double q-integrals) holds. Let , and be three functions defined on with . Then we have

According to the definition of q-integral, it is easy to obtain that double q-integral is

Due to discrete Cauchy-Schwarz inequality with weight coefficient, we have

Next, we prove that Lemma 2 holds. Let be defined by
Multiplying both sides of (5) by and integrating the resulting identity with respect to τ and ρ from 0 to t, then applying the Cauchy-Schwarz inequality for double q-integrals, we obtain (4). □
Lemma 3 Let and f be a function defined on . Then, for all and , we have

Proof Multiplying both sides of (3) by and integrating the resulting identity with respect to ρ from 0 to t, we obtain

which implies (6). □
Theorem 1 Let f and g be two functions defined on satisfying (A). Then, for all and , we have
Proof Let f and g be two functions defined on satisfying (A). Multiplying both sides of (6) by and integrating the resulting identity with respect to τ and ρ from 0 to t, we can state that

Applying the Cauchy-Schwarz inequality for double q-integrals, we have

Since and , we have

Thus,
Combining (9) and (10), from Lemma 1, we deduce that

Now by using the elementary inequality , , we can state that
From (11) and (12), we obtain (7). □
Theorem 2 Let f and g be two functions defined on satisfying (A). Then, for all , and , we have

Proof Since and , then we can write
Applying Lemma 3 to f and g, then by using Lemma 2 and the formula (13), we obtain Theorem 2. □
4 The other fractional q-integral inequalities
For the sake of simplicity, we always assume that denotes and all of fractional q-integrals are finite in this section.
Theorem 3 Let f and g be two functions defined on and satisfying . Then the following inequalities hold:
-
(a)
.
-
(b)
.
-
(c)
.
-
(d)
.
Proof According to the well-known Young inequality,
Putting and , , we have
Multiplying both sides of (6) by , we obtain

Integrating the preceding identity with respect to τ and ρ from 0 to t, we can state that
which implies (a). The rest of inequalities can be proved in the same manner by the next choice of the parameters in the Young inequality:
-
(b)
, .
-
(c)
, , ().
-
(d)
, , ().
Repeating the foregoing arguments, we obtain (b)-(d). □
Theorem 4 Let f and g be two functions defined on and satisfying . Then the following inequalities hold:
-
(a)
.
-
(b)
.
-
(c)
.
Proof As a previous one, the proof is based on the Young inequality with the following appropriate choice of parameters:
-
(a)
, .
-
(b)
, , .
-
(c)
, , .
□
Theorem 5 Let f and g be two positive functions defined on such that for all ,
Then the following inequalities hold:
-
(a)
.
-
(b)
.
-
(c)
.
Proof It follows from (15) and
Multiplying both sides of (15) by and integrating the resulting identity with respect to τ from 0 to t, we can get
On the other hand, it follows from and that
According to (17) and (18), we have
which implies (a). By a few transformations of (a), similarly, we obtain (b) and (c). □
Corollary 1 Under the conditions of Theorem 5, if , , then it follows from the arithmetric-geometric mean inequality that
which implies that
Theorem 6 Let f and g be two positive functions on and
Then the following inequalities hold:
-
(a)
.
-
(b)
.
-
(c)
.
Proof Under the conditions satisfied by the functions f and g, we have
Applying Theorem 6, we get the inequality (a) and using it, we have (b) and (c). □
Corollary 2 Let f be a positive function on satisfying (19). Then the following inequality holds:
Theorem 7 Let f and g be two positive functions on and
and be a real number, then the following inequality holds:
for , or reverse for . Especially, for , we have
Proof The inequality is based on the Lah-Ribaric inequality [[18], p.9] and [[19], p.123]. □
Theorem 8 Let f and g be two positive functions on and be a real number. Then the following inequality holds:
for , or reverse for .
Proof The above inequality is obtained via the Jensen inequality for the convex functions. □
Corollary 3 Let f be a positive function on and be a real number. Then the following inequality holds:
for , or reverse for .
Theorem 9 Let p, f and g be three positive functions on satisfying (19). If , , then the following inequalities hold:


Proof Since on , we have
Multiplying both sides of (23) by , we get
From (24) and arithmetric-geometric mean inequality, we obtain

which implies (21).
Replacing p and f by and in (25), respectively, and , we get

which implies (22). □
Corollary 4 Let p, f and g be three positive functions on satisfying (20). If , , then the following inequality holds:
Proof Replacing , and by m, M and in (24), and multiplying both sides by and integrating the resulting identity with respect to τ from 0 to t, we get (25). □
Theorem 10 Let p, f and g be three functions on with .
-
(a)
If there exist four constants such that for all , then
(27)
Moreover, if , then


-
(b)
If there exist four constants such that for all , then
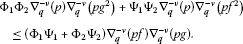 (30)
(30) -
(c)
If and , then
(31) -
(d)
If and , then
(32)
Proof Case (a). It follows from the assumption that
for all , which implies that
Multiplying both sides of (33) by and integrating the resulting identity with respect to τ from 0 to t, we obtain the left-hand side of (27). Furthermore, by Cauchy’s inequality, we get the right-hand side of (27).
Multiplying both sides of the inequality
by , we get (28).
On the other hand, it follows from and that
According to (27) and (34), we have
which implies (29).
Case (b). It follows from the assumption that
for all , which implies that

Multiplying both sides of (35) by and integrating the resulting identity with respect to τ and ρ from 0 to t, respectively, we obtain (30).
Case (c) and (d). It follows from Cauchy’s inequality that
Combining (a), (b) and the preceding two inequalities, we see that
which implies (31). Furthermore,
which implies (32). □
Theorem 11 Let p, f and g be three positive functions on with . Then we have
Moreover, under the assumptions of (a) and (b) in Theorem 10, the following inequality holds:

Proof First of all, we give the proof of (36). By Cauchy’s inequality and the element inequality , for all , we have

which implies (36).
Next, we prove that (37) holds. It follows from (a) and (b) in Theorem 10 that
Combining the preceding two inequalities and the element inequality , we see that

which implies (37). □
References
Anastassiou GA: Opial type inequalities involving fractional derivatives of two functions and applications. Comput. Math. Appl. 2004, 48: 1701–1731. 10.1016/j.camwa.2003.08.013
Anastassiou GA: Multivariate fractional Ostrowski type inequalities. Comput. Math. Appl. 2007, 54: 434–447. 10.1016/j.camwa.2007.01.024
Anastassiou GA: Hilbert-Pachpatte type fractional integral inequalities. Math. Comput. Model. 2009, 49: 1539–1550. 10.1016/j.mcm.2008.05.059
Anastassiou GA: Opial type inequalities involving Riemann-Liouville fractional derivatives of two functions with applications. Math. Comput. Model. 2008, 48: 344–374. 10.1016/j.mcm.2007.09.017
Denton Z, Vatsala AS: Fractional integral inequalities and applications. Comput. Math. Appl. 2010, 59: 1087–1094. 10.1016/j.camwa.2009.05.012
Belarbi S, Dahmani Z: On some new fractional integral inequalities. J. Inequal. Pure Appl. Math. 2009., 10: Article ID 86
Dahmani Z, Tabharit L, Taf S: New generalisations of Grüss inequality using Riemann-Liouville fractional integrals. Bull. Math. Anal. Appl. 2010, 2: 93–99.
Öğünmez H, Özkan U: Fractional quantum integral inequalities. J. Inequal. Appl. 2011., 2011: Article ID 787939
Bohner M, Ferreira RAC: Some discrete fractional inequalities of Chebyshev type. Afr. Diaspora J. Math. (N.S.) 2011, 11(2):132–137.
Yang W: Some new fractional quantum integral inequalities. Appl. Math. Lett. 2012, 25: 963–969. 10.1016/j.aml.2011.11.005
Marinković S, Rajković P, Stanković M: The inequalities for some types of q -integrals. Comput. Math. Appl. 2008, 56: 2490–2498. 10.1016/j.camwa.2008.05.035
Yeh C, et al.: Some complements of Cauchy’s inequality on time scales. J. Inequal. Appl. 2006., 2006: Article ID 97430
Bohner M, Peterson A: Dynamic Equations on Time Scales. Birkhäuser, Boston; 2001.
Atici F, Eloe P: Fractional q -calculus on a time scale. J. Nonlinear Math. Phys. 2007, 14: 341–352. 10.2991/jnmp.2007.14.3.4
Rajković P, Marinković S, Stanković M: A generalization of the concept of q -fractional integrals. Acta Math. Sin. Engl. Ser. 2009, 25: 1635–1646. 10.1007/s10114-009-8253-x
Al-Salam WA: Some fractional q -integrals and q -derivatives. Proc. Edinb. Math. Soc. 1966/1967, 15(2):135–140. 10.1017/S0013091500011469
Agarwal RP: Certain fractional q -integrals and q -derivatives. Proc. Camb. Philos. Soc. 1969, 66: 365–370. 10.1017/S0305004100045060
Mitrinović DS, Pečarić JE, Fink AM: Classical and New Inequalities in Analysis. Kluwer Academic, Dordrecht; 1993.
Dragomir SS: A survey on Cauchy-Bunyakovsky-Schwarz type discrete inequalities. J. Inequal. Pure Appl. Math. 2003., 4(3): Article ID 63
Acknowledgements
The authors sincerely thank the editor and reviewers for their valuable suggestions and useful comments that have led to the present improved version of the original manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, C., Yang, W. & Zhao, Q. Some new fractional q-integral Grüss-type inequalities and other inequalities. J Inequal Appl 2012, 299 (2012). https://doi.org/10.1186/1029-242X-2012-299
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-299