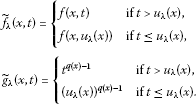On the sub-supersolution method for $p(x)$-Kirchhoff type equations

Abstract

This paper deals with the sub-supersolution method for the $p(x)$-Kirchhoff type equations. A sub-supersolution principle for the Dirichlet problems involving $p(x)$-Kirchhoff is established. A strong comparison theorem for the $p(x)$-Kirchhoff type equations is presented. We also give some applications of the abstract theorems obtained in this paper to the eigenvalue problems for the $p(x)$-Kirchhoff type equation.

MSC:35D05, 35D10, 35J60.

1 Introduction

In this paper, we study the following problem:

$$\{\begin{array}{c}-M(t)div({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u)=f(x,u)\text{in }\mathrm{\Omega },\hfill \\ u=0\text{on }\partial \mathrm{\Omega },\hfill \end{array}$$

(1.1)

where Ω is a bounded smooth domain in ${\mathbb{R}}^N$ with $N\ge 1$, $p=p(x)\in C(\overline{\mathrm{\Omega }})$ with $1<p^{-}:={inf}_{\mathrm{\Omega }}p(x)\le p^{+}:={sup}_{\mathrm{\Omega }}p(x)<+\mathrm{\infty }$, $f\in C(\overline{\mathrm{\Omega }}\times \mathbb{R},\mathbb{R})$, $M(t)$ is a continuous function with $t:={\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx$ and satisfies the following condition:

($M_0$) $M:[0,+\mathrm{\infty })\to (m_0,+\mathrm{\infty })$ is a continuous and increasing function with $m_0>0$.

The operator $-div({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u)$ is said to be $p(x)$-Laplacian. The study of various mathematical problems with the variable exponent growth condition has received considerable attention in recent years. These problems are interesting in applications and raise many difficult mathematical problems. We refer the reader to [1] for an overview of and references on this subject.

The solvability of the problem (1.1) can be studied by several approaches; for example, the variational method (see, e.g., [2]). It is well known that, compared with other methods, the sub-supersolution method, or the order method, when it is applicable, has some distinctive advantages. For example, it usually gives some order properties of the solutions. For the applications of the sub-supersolution method to semilinear and quasilinear elliptic problems, we refer to [3, 4] and the references therein. In [3], Fan established a sub-supersolution principle for Dirichlet problems involving $p(x)$-Laplacian and a strong comparison theorem for $p(x)$-Laplacian equations. The goal of this paper is to study the sub-supersolution method for (1.1), which is a new research topic.

The problem (1.1) is related to the stationary problem of a model introduced by Kirchhoff [5]. We refer the reader to [6] for an overview of and references on this subject.

In [3], the sub-supersolution principle for $p(x)$-Laplacian equations established by Fan is based on the properties of $p(x)$-Laplace, the regularity results and the comparison principle. The aim of the present paper is to establish a sub-supersolution principle for $p(x)$-Kirchhoff equations.

The rest of this paper is organized as follows. In Section 2, we establish a general principle of the sub-supersolution method for the problem (1.1) based on the regularity results and the comparison principle. In Section 3, we give a special strong comparison principle for the $p(x)$-Kirchhoff. In Section 4, we give an application of our abstract theorems.

2 Sub-supersolution principle

In this section, we give a general principle of sub-supersolution method for the problem (1.1) based on the regularity results and the comparison principle. We would like to point out that the comparison principle in this section (see Theorem 2.2) is a generalization of Proposition 2.3 of [3]. In addition to the principle of sub-supersolution, we shall establish also a generalization of Theorem 2.1 of [3]. For simplicity, we write $X=W_0^{1,p(x)}(\mathrm{\Omega })$.

Definition 2.1 (1) We say that $u\in X$ is a weak solution of (1.1) if

$$M\left({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx\right){\int }_{\mathrm{\Omega }}{|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u\mathrm{\nabla }\phi dx={\int }_{\mathrm{\Omega }}f(x,u)\phi dx$$

for any $\phi \in X$.

• (2) $u\in W^{1,p(x)}$ is called a subsolution (respectively a supersolution) of (1.1) if $u\le (\text{respectively }\ge )0$ on ∂ Ω and, for all $\phi \in X$ with $\phi \ge 0$,

  $$M\left({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx\right){\int }_{\mathrm{\Omega }}{|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u\mathrm{\nabla }\phi dx\le (\text{respectively }\ge ){\int }_{\mathrm{\Omega }}f(x,u)\phi dx.$$

Regularity results and comparison principles are the basis of the sub-supersolution method. For the regularity results in the variable exponent case, see [7–9]. More precisely, for the $L^{\mathrm{\infty }}$ and $C^{0,\alpha }$ regularity, see [8]; for the local $C^{1,\alpha }$ regularity of the minimizers of the corresponding integral functional, see [7]; for the global $C^{1,\alpha }$ regularity, see [9].

If f is independent of u, we have

Theorem 2.1 If ($M_0$) holds and $f(x,u)=f(x)$, $f\in L^{\frac{q(x)}{q(x)-1}}(\mathrm{\Omega })$, then (1.1) has a unique weak solution.

Proof Clearly, $(f,v):={\int }_{\mathrm{\Omega }}f(x)vdx$ (for any $v\in X$) defines a continuous linear functional on X. According to Theorem 4.1 of [10], ${\mathrm{\Phi }}^{\prime }$ is a homeomorphism. So, (1.1) has a unique solution, where $\mathrm{\Phi }(u)=\hat{M}({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx)$. □

From Theorem 2.1 we know that, for a given $h\in L^{\frac{q(x)}{q(x)-1}}(\mathrm{\Omega })$, where $q\in C_{+}(\overline{\mathrm{\Omega }})$ and

$$1<q(x)<p^{\ast }(x),\mathrm{\forall }x\in \overline{\mathrm{\Omega }},$$

(2.1)

the problem

$$\{\begin{array}{c}-M(t)div({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u)=h(x)\text{in }\mathrm{\Omega },\hfill \\ u=0\text{on }\partial \mathrm{\Omega }\hfill \end{array}$$

(2.2)

has a unique solution $u\in X$ under the condition ($M_0$). We denote by $K(h):=u$ the unique solution. K is called a solution operator for (2.2).

From the regularity results and the embedding theorems, we can obtain the properties of the solution operator K as follows.

Proposition 2.1 (1) If ($M_0$) holds, the mapping $K:L^{\frac{q(x)}{q(x)-1}}(\mathrm{\Omega })\to X$ is continuous and bounded. Moreover, the mapping $K:L^{\frac{q(x)}{q(x)-1}}(\mathrm{\Omega })\hookrightarrow L^{q(x)}(\mathrm{\Omega })$ is completely continuous since the embedding $X\hookrightarrow L^{q(x)}(\mathrm{\Omega })$ is compact.

• (2) If ($M_0$) holds and p is log-Hölder continuous on $\overline{\mathrm{\Omega }}$, then the mapping $K:L^{\mathrm{\infty }}(\mathrm{\Omega })\to C^{0,\alpha }(\overline{\mathrm{\Omega }})$ is bounded, and hence the mapping $K:L^{\mathrm{\infty }}(\mathrm{\Omega })\to C(\overline{\mathrm{\Omega }})$ is completely continuous.

• (3) If ($M_0$) holds and p is Hölder continuous on $\overline{\mathrm{\Omega }}$, then the mapping $K:L^{\mathrm{\infty }}(\mathrm{\Omega })\to C^{1,\alpha }(\overline{\mathrm{\Omega }})$ is bounded, and hence the mapping $K:L^{\mathrm{\infty }}(\mathrm{\Omega })\to C^1(\overline{\mathrm{\Omega }})$ is completely continuous.

Definition 2.2 Let $u,v\in W^{1,p(x)}(\mathrm{\Omega })$. We say that $-M(I_0(u)){\mathrm{\Delta }}_{p(x)}(u)\le -M(I_0(v)){\mathrm{\Delta }}_{p(x)}(v)$ if for all $\phi \in X$ with $\phi \ge 0$,

$$M(I_0(u)){\int }_{\mathrm{\Omega }}{|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u\mathrm{\nabla }\phi dx\le M(I_0(v)){\int }_{\mathrm{\Omega }}{|\mathrm{\nabla }v|}^{p(x)-2}\mathrm{\nabla }v\mathrm{\nabla }\phi dx,$$

(2.3)

where $I_0(u)={\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx$.

Now we give the comparison principle as follows.

Theorem 2.2 (1) Let $u,v\in W^{1,p(x)}(\mathrm{\Omega })$ and ($M_0$) hold. If $-M(I_0(u)){\mathrm{\Delta }}_{p(x)}(u)\le -M(I_0(v))\times {\mathrm{\Delta }}_{p(x)}(v)$ and ${(u-v)}^{+}\in W_0^{1,p(x)}(\mathrm{\Omega })$, then $u\le v$ in Ω.

• (2) Under the conditions of (1) above, let in addition $u,v\in C(\overline{\mathrm{\Omega }})$ and denote $S=\{x\in \mathrm{\Omega }:u(x)=v(x)\}$. If S is a compact subset of Ω, then $S=\mathrm{\varnothing }$.

Proof (1) Taking $\lambda =0$ in the proof of Theorem 3.2 of [11], we can get the conclusion.

• (2) Suppose that S is a compact subset of Ω and $S\ne \mathrm{\varnothing }$. Then there is an open subset ${\mathrm{\Omega }}_3$ of Ω such that $S\subset {\mathrm{\Omega }}_3\subset {\overline{\mathrm{\Omega }}}_3\subset \mathrm{\Omega }$. Thus $u<v$ on $\partial {\mathrm{\Omega }}_3$ and consequently there is an $\epsilon >0$ such that $u<v-\epsilon$ on $\partial {\mathrm{\Omega }}_3$. Noting that $\mathrm{\nabla }(v-\epsilon )=\mathrm{\nabla }v$ and applying the conclusion (1) to u and $v-\epsilon$ on ${\mathrm{\Omega }}_3$, we obtain $u\le v-\epsilon$ in ${\mathrm{\Omega }}_3$, which contradicts $u=v$ on S. □

It follows from Theorem 2.2(1) that the solution operator K is increasing under the condition ($M_0$), that is, $K(u)\le K(v)$ if $u\le v$. We define $T(u)=K(f(x,u))$. It is easy to see that if u is a subsolution (respectively a supersolution) of (1.1), then $u\le T(u)$ (respectively $u\ge T(u)$), and u is a solution of (1.1) if and only if $u=T(u)$, i.e., u is a fixed point of T.

The basic principle of the sub-supersolution method for (1.1) is the following result.

Theorem 2.3 Let ($M_0$) hold and suppose that f satisfies the sub-critical growth condition

$$|f(x,t)|\le c_1+c_2{|t|}^{q(x)-1},\mathrm{\forall }x\in \mathrm{\Omega },\mathrm{\forall }t\in \mathbb{R},$$

and the function $f(x,t)$ is nondecreasing in $t\in \mathbb{R}$. If there exist a subsolution $u_0\in W^{1,p(x)}(\mathrm{\Omega })$ and a supersolution $v_0\in W^{1,p(x)}(\mathrm{\Omega })$ of (1.1) such that $u_0\le v^0$, then (1.1) has a minimal solution $u_{\ast }$ and a maximal solution $v^{\ast }$ in the order interval $[u_0,v^0]$, i.e., $u_0\le u_{\ast }\le v^{\ast }\le v^0$ and if u is any solution of (1.1) such that $u_0\le u\le v^0$, then $u_{\ast }\le u\le v^{\ast }$.

Proof Define $T(u)=K(f(x,u))$. Then, under the assumptions of Theorem 2.3, $T:L^{q(x)}(\mathrm{\Omega })\to L^{q(x)}(\mathrm{\Omega })$ is completely continuous and increasing, $u_0\le v^0$, $u_0,v^0\in L^{q(x)}(\mathrm{\Omega })$, $u_0\le T(u_0)$, $v^0\ge T(v^0)$, and consequently $T:[u_0,v^0]\to [u_0,v^0]$. It is clear that the cone of all nonnegative functions in $L^{q(x)}(\mathrm{\Omega })$ is normal. Noting the minimal (maximal) fixed point (see [4]) of T is the minimal (maximal) solution of (1.1), so our Theorem 2.3 now follows by applying the well-known fixed point theorem for the increasing operator on the order interval (see, e.g., [4]). □

In the practical problems, it is often known that the subsolution $u_0$ and the supersolution $v^0$ are of class $L^{\mathrm{\infty }}(\mathrm{\Omega })$, so the restriction on the growth condition of f is needless. Hence, the following theorem is more suitable.

Theorem 2.4 Let ($M_0$) hold and suppose that $u_0,v^0\in W^{1,p(x)}(\mathrm{\Omega })\cap L^{\mathrm{\infty }}(\mathrm{\Omega })$, $u_0$ and $v^0$ are a subsolution and a supersolution of (1.1) respectively, and $u_0\le v^0$. If $f\in C(\overline{\mathrm{\Omega }}\times \mathbb{R},\mathbb{R})$ satisfies the condition

$$(F_1)f(x,t)\mathit{\text{is nondecreasing in}}t\in [inf{u}_0(x),sup{v}^0(x)],$$

then the conclusion of Theorem  2.3 is valid.

The above results show that the general principle of the sub-supersolution method for $p(x)$-Kirchhoff type equations (1.1) is of the same type as in the case of $p(x)$-Laplacian type equations. An essential prerequisite for the sub-supersolution method is to find a subsolution $u_0$ and a supersolution $v^0$ such that $u_0\le v^0$. It is well known that the homogeneity of the p-Laplacian operator and the positivity of the first eigenvalue of p-Laplacian Dirichlet problem play an important role in finding sub- and supersolutions of the p-Laplacian equation [12]. Unlike the p-Laplacian, when $p(x)$ is not identical with a constant, the $p(x)$-Laplacian operator is inhomogeneous and usually the infimum of its eigenvalues is 0. It is obvious that the eigenvalues of (1.1) are ${\mu }_j=M({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }{\phi }_j|}^{p(x)}dx){\lambda }_j$, where ${\lambda }_j$ and ${\phi }_j$ are, respectively, the eigenvalues and eigenfunctions of $-{\mathrm{\Delta }}_{p(x)}$ in X. Thus, usually, the infimum of ${\mu }_j$ is also 0. Therefore, it is often difficult to find a subsolution $u_0$ and a supersolution $v^0$ of (1.1) with $u_0\le v^0$.

At the end of this section, we give a lemma which is useful to find a supersolution of (1.1). We denote by $C_0$ the best embedding constant of $W_0^{1,1}(\mathrm{\Omega })\subset L^{\frac{N}{N-1}}(\mathrm{\Omega })$.

Lemma 2.1 Let ($M_0$) hold, $\mathcal{M}>0$ and let u be the unique solution of the problem

$$\{\begin{array}{c}-M(t)div({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u)=\mathcal{M}\mathit{\text{in}}\mathrm{\Omega },\hfill \\ u=0\mathit{\text{on}}\partial \mathrm{\Omega }.\hfill \end{array}$$

(2.4)

Set $h=\frac{m_0{p}^{-}}{2{|\mathrm{\Omega }|}^{1/N}{C}_0}$. Then, when $\mathcal{M}\ge h$, ${|u|}_{\mathrm{\infty }}\le C^{\ast }{\mathcal{M}}^{1/(p^{-}-1)}$, and when $\mathcal{M}<h$, ${|u|}_{\mathrm{\infty }}\le C^{\ast }{\mathcal{M}}^{1/(p^{+}-1)}$, where $C^{\ast }$ and $C_{\ast }$ are positive constants depending on $p^{+}$, $p^{-}$, N, $|\mathrm{\Omega }|$, $C_0$ and $m_0$.

Proof Let u be the solution of (2.4), Theorem 2.2 implies $u\ge 0$. For $k\ge 0$, set $A_k=\{x\in \mathrm{\Omega }:u(x)>k\}$. Taking ${(u-k)}^{+}$ as a test function in (2.4) and using the Young inequality, we have

$$\begin{array}{rcl}{\int }_{A_k}{|\mathrm{\nabla }u|}^{p(x)}dx& =& \frac{\mathcal{M}}{M(t)}{\int }_{A_k}(u-k)dx\\ \le & \frac{\mathcal{M}{|\mathrm{\Omega }|}^{1/N}{C}_0}{m_0{p}^{-}}{\int }_{A_k}{\epsilon }^{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx+\frac{\mathcal{M}{|A_k|}^{1/N}{C}_0}{m_0{(p^{+})}^{\prime }}{\int }_{A_k}{\epsilon }^{-p^{\prime }(x)}dx.\end{array}$$

(2.5)

When $\mathcal{M}\ge h$, taking

$$\epsilon ={\left(\frac{m_0{p}^{-}}{2\mathcal{M}{|\mathrm{\Omega }|}^{1/N}{C}_0}\right)}^{1/p^{-}}={\left(\frac{h}{\mathcal{M}}\right)}^{1/p^{-}},$$

then $\epsilon \le 1$ and

$$\frac{\mathcal{M}{|\mathrm{\Omega }|}^{1/N}{C}_0}{m_0{p}^{-}}{\int }_{A_k}{\epsilon }^{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx\le \frac{\mathcal{M}{|\mathrm{\Omega }|}^{1/N}{C}_0}{m_0{p}^{-}}{\epsilon }^{p^{-}}{\int }_{A_k}{|\mathrm{\nabla }u|}^{p(x)}dx=\frac{1}{2}{\int }_{A_k}{|\mathrm{\nabla }u|}^{p(x)}dx.$$

Consequently, from this and (2.5), it follows that

$${\int }_{A_k}{|\mathrm{\nabla }u|}^{p(x)}dx\le \frac{2\mathcal{M}{|A_k|}^{1/N}{C}_0}{m_0{(p^{+})}^{\prime }}{\int }_{A_k}{\epsilon }^{-p^{\prime }(x)}dx\le \frac{2\mathcal{M}{C}_0{\epsilon }^{-{(p^{-})}^{\prime }}}{m_0{(p^{+})}^{\prime }}{|A_k|}^{1+1/N}.$$

(2.6)

From (2.5) and (2.6), we have

$$\begin{array}{rcl}{\int }_{A_k}(u-k)dx& =& \frac{M(t)}{\mathcal{M}}{\int }_{A_k}{|\mathrm{\nabla }u|}^{p(x)}dx\\ \le & M\left(\frac{2\mathcal{M}{C}_0{\epsilon }^{-{(p^{-})}^{\prime }}}{p^{-}{m}_0{(p^{+})}^{\prime }}{|\mathrm{\Omega }|}^{1+1/N}\right)\frac{2C_0{\epsilon }^{-{(p^{-})}^{\prime }}}{m_0{(p^{+})}^{\prime }}{|A_k|}^{1+1/N}.\end{array}$$

(2.7)

By Lemma 5.1 in [[13], Chapter 2], (2.7) implies that

$${|u|}_{\mathrm{\infty }}\le \gamma (N+1){|\mathrm{\Omega }|}^{1/N},$$

(2.8)

where $\gamma =M(\frac{2\mathcal{M}{C}_0{\epsilon }^{-{(p^{-})}^{\prime }}}{p^{-}{m}_0{(p^{+})}^{\prime }}{|\mathrm{\Omega }|}^{1+1/N})\frac{2C_0{\epsilon }^{-{(p^{-})}^{\prime }}}{m_0{(p^{+})}^{\prime }}$. From (2.7) and (2.8), we obtain

$${|u|}_{\mathrm{\infty }}\le C^{\ast }{\mathcal{M}}^{1/(p^{-}-1)},$$

where

$$C^{\ast }=\frac{(N+1){(2C_0)}^{{(p^{-})}^{\prime }}}{{(p^{+})}^{\prime }{m}_0^{{(p^{-})}^{\prime }}{(p^{-})}^{{(p^{-})}^{\prime }/p^{-}}}{|\mathrm{\Omega }|}^{{(p^{-})}^{\prime }/N}M\left(\frac{{(2\mathcal{M}{C}_0)}^{{(p^{-})}^{\prime }}}{p^{-}{(p^{+})}^{\prime }{m}_0^{{(p^{-})}^{\prime }}{(p^{-})}^{{(p^{-})}^{\prime }/p^{-}}}{|\mathrm{\Omega }|}^{{(p^{-})}^{\prime }/N}\right).$$

When $\mathcal{M}<h$, taking

$$\epsilon ={\left(\frac{m_0{p}^{-}}{2\mathcal{M}{|\mathrm{\Omega }|}^{1/N}{C}_0}\right)}^{1/p^{+}}={\left(\frac{h}{\mathcal{M}}\right)}^{1/p^{+}}$$

(noting that in this case $\epsilon >1$) and using arguments similar to those above, we can obtain

$${|u|}_{\mathrm{\infty }}\le C^{\ast }{\mathcal{M}}^{1/(p^{+}-1)},$$

where

$$C^{\ast }=\frac{(N+1){(2C_0)}^{{(p^{+})}^{\prime }}}{{(p^{+})}^{\prime }{m}_0^{{(p^{+})}^{\prime }}{(p^{-})}^{{(p^{+})}^{\prime }/p^{+}}}{|\mathrm{\Omega }|}^{{(p^{+})}^{\prime }/N}M\left(\frac{{(2\mathcal{M}{C}_0)}^{{(p^{+})}^{\prime }}}{p^{-}{(p^{+})}^{\prime }{m}_0^{{(p^{+})}^{\prime }}{(p^{-})}^{{(p^{+})}^{\prime }/p^{+}}}{|\mathrm{\Omega }|}^{{(p^{+})}^{\prime }/N}\right).$$

The proof is complete. □

Remark 2.1 We would like to point out that the fact that a solution of (2.4) is bounded in $L^{\mathrm{\infty }}(\mathrm{\Omega })$ is useful for finding a supersolution of (1.1). Indeed, the fact can be used to estimate the relation of nonlinearity and ℳ (for details, see the proof of Theorem 4.1).

3 A strong comparison principle for $p(x)$-Kirchhoff problem

The energy functional associated with the problem (1.1) is

$$J(u)=\hat{M}(I_0(u))-{\int }_{\mathrm{\Omega }}F(x,u)dx,$$

where $\hat{M}(t)={\int }_0^{t}M(\tau )d\tau$ and $F(x,u)={\int }_0^{u}f(x,t)dt$. In this section, we give a special strong comparison principle for the $p(x)$-Kirchhoff, which is suitable for finding a positive $C^1$ local minimizer of the integral functional J in the $C^1$ topology. In [14], Fan established a Brezis-Nirenberg type theorem (Theorem 1.1 of [14]), which asserts that every local minimizer of J in the $C^1(\mathrm{\Omega })$ topology is also a local minimizer of J in the $W_0^{1,p(x)}(\mathrm{\Omega })$ topology. Applying this theorem, we have the following special form.

Theorem 3.1 Let ($M_0$), (2.1) hold and let $u_0\in X$ be a local minimizer (resp. a strictly local minimizer) of J in the $C^1(\mathrm{\Omega })$ topology. Then $u_0$ is a local minimizer (resp. a strictly local minimizer) of J in the X topology.

Applying Theorem 1.1 of [15], we can easily get the following strong maximum principle.

Theorem 3.2 Suppose that $p(x)\in C_{+}(\overline{\mathrm{\Omega }})\cap C^1(\overline{\mathrm{\Omega }})$, $u\in X$, $u\ge 0$ and $u\not\equiv 0$ in Ω. If

$$-M(t)(div\left({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u\right)-d(x){|u|}^{q(x)-2}u)\ge 0,$$

where $t={\int }_{\mathrm{\Omega }}(\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}+\frac{1}{q(x)}d(x){|u|}^{q(x)})dx$, $M(t)\ge m_0>0$, $0\le d(x)\in L^{\mathrm{\infty }}(\mathrm{\Omega })$, $q(x)\in C(\overline{\mathrm{\Omega }})$ with $p(x)\le q(x)\le p^{\ast }(x)$, then $u>0$ in Ω.

Now we give a special strong comparison principle for the $p(x)$-Kirchhoff.

Theorem 3.3 Let ($M_0$) hold and suppose that $u,v\in C^1(\overline{\mathrm{\Omega }})$, $u\ge v$ in Ω, $g,h\in L^{\mathrm{\infty }}(\mathrm{\Omega })$,

$$-M(I_0(u)){\mathrm{\Delta }}_{p(x)}u=g(x)\ge h(x)=-M(I_0(v)){\mathrm{\Delta }}_{p(x)}v\mathit{\text{in}}\mathrm{\Omega },$$

(3.1)

and $g(x)\not\equiv h(x)$ in Ω. If

$$\frac{\partial u}{\partial \mathbf{n}}>0,\frac{\partial v}{\partial \mathbf{n}}>0\mathit{\text{on}}\partial \mathrm{\Omega },$$

where n is the inward unit normal on ∂ Ω, then $u>v$ in Ω and there is a positive constant ε such that

$$\frac{\partial (u-v)}{\partial \mathbf{n}}\ge \epsilon \mathit{\text{on}}\partial \mathrm{\Omega }.$$

(3.2)

Proof We denote by ${\mathbf{n}}_y$ the inward unit normal at $y\in \partial \mathrm{\Omega }$. For $\delta >0$, set ${\mathrm{\Omega }}_{\delta }=\{x\in \mathrm{\Omega }:dist(x,\partial \mathrm{\Omega })<\delta \}$. Denoting $A(x,\eta )=M(I_0(\eta )){|\eta |}^{p(x)-2}\eta$, as in the proof of [3], we have

$$u-v\ge 0\text{in }{\mathrm{\Omega }}_{\delta }.$$

We claim that $u-v\not\equiv 0$ in ${\mathrm{\Omega }}_{\delta }$. Indeed, if $u\equiv v$ in ${\mathrm{\Omega }}_{\delta }$, then $g\equiv h$ in ${\mathrm{\Omega }}_{\delta }$, and consequently $g(x)\not\equiv h(x)$ in $\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }$. Take $\phi \in X$ such that $\phi >0$ in Ω, $\phi =1$ on $\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }$. By (3.1) and the property of φ, we have

$$\begin{array}{rcl}{\int }_{\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }}g(x)\phi (x)dx& =& M\left({\int }_{\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx\right){\int }_{\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }}{|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u\mathrm{\nabla }\phi dx=0\\ =& M\left({\int }_{\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }}\frac{1}{p(x)}{|\mathrm{\nabla }v|}^{p(x)}dx\right){\int }_{\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }}{|\mathrm{\nabla }v|}^{p(x)-2}\mathrm{\nabla }v\mathrm{\nabla }\phi dx\\ =& {\int }_{\mathrm{\Omega }\setminus {\mathrm{\Omega }}_{\delta }}h(x)\phi (x)dx,\end{array}$$

which contradicts ${\int }_{\mathrm{\Omega }}g(x)\phi (x)dx>{\int }_{\mathrm{\Omega }}h(x)\phi (x)dx$. Hence the claim is true. So, by the well-known strong maximum principle for linear elliptic equations, $u>v$ in ${\mathrm{\Omega }}_{\delta }$ and (3.2) holds. Setting $S=\{x\in \mathrm{\Omega }:u(x)=v(x)\}$, then S is a compact subset of Ω. By Theorem 2.2(2), $S=\mathrm{\varnothing }$, hence $u>v$ in Ω and the proof is complete. □

The following theorem provides a method to find a positive $C^1$ local minimizer of the integral functional J in the $C^1$ topology.

Theorem 3.4 Let ($M_0$) hold and suppose that $u_0,v^0\in X$ are a subsolution and a supersolution of (1.1) respectively, $-M(I(u_0)){\mathrm{\Delta }}_{p(x)}{u}_0=g(x)$, $-M(I(v^0)){\mathrm{\Delta }}_{p(x)}{v}^0=h(x)$, $g,h\in L^{\mathrm{\infty }}(\mathrm{\Omega })$, $0\le g\le h$, $g(x)\not\equiv h(x)$ and $0\le u_0\le v^0$ in Ω. Suppose that $p\in C^1(\overline{\mathrm{\Omega }})$, $f\in C(\overline{\mathrm{\Omega }}\times \mathbb{R},\mathbb{R})$ satisfies the condition of Theorem  2.3. If neither $u_0$ nor $v^0$ is a solution of (1.1), or neither $u_0$ nor $v^0$ is a minimizer of J on $[u_0,v^0]\cap X$ in the case of being a solution of (1.1), then there exists $u_{\ast }\in [u_0,v^0]\cap C^{1,\alpha }(\overline{\mathrm{\Omega }})$ such that $J(u_{\ast })=inf\{J(u):u\in [u_0,v^0]\cap X\}$, $u_{\ast }$ is a solution of (1.1) and $u_{\ast }$ is a local minimizer of J in the $C^1$ topology.

Proof The proof is similar to the proof of [3], we omit it here (for details, see the proof of Theorem 3.3 in [3]). □

4 Applications

As an application of the above abstract theorems, let us consider the following eigenvalue problem:

$$\{\begin{array}{c}-M({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx)div({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u)=\lambda f(x,u)+\mu {|u|}^{q(x)-2}u\text{in }\mathrm{\Omega },\hfill \\ u>0\text{in }\mathrm{\Omega },u=0\text{on }\partial \mathrm{\Omega },\hfill \end{array}$$

(4.1)

where Ω is a bounded smooth domain in ${\mathbb{R}}^N$, $p\in C^1(\overline{\mathrm{\Omega }})$, $q\in C(\overline{\mathrm{\Omega }})$, $q^{-}>p^{+}$, $f\in C(\overline{\mathrm{\Omega }}\times \mathbb{R},\mathbb{R})$, $f(x,t)\ge 0$ for $x\in \mathrm{\Omega }$ and $t\ge 0$, $f(x,t)$ is nondecreasing in $t\ge 0$, $\mu \ge 0$ is fixed. The energy functional associated with the problem (4.1) is

$$J_{\lambda }(u)=\hat{M}\left({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx\right)-\lambda {\int }_{\mathrm{\Omega }}F(x,u)dx-\mu {\int }_{\mathrm{\Omega }}\frac{{|u|}^{q(x)}}{q(x)}dx,\mathrm{\forall }u\in X,$$

where $F(x,t)={\int }_0^{t}f(x,s)ds$.

Firstly, we recall the (PS) _c condition and the mountain pass lemma which we shall use later.

Definition 4.1 Let X be a Banach space. We say that I satisfies the (PS) _c condition in X if any sequence $\{u_n\}\subset X$, such that $|I(u_n)|\le c$ and $I^{\prime }(u_n)\to 0$ as $n\to +\mathrm{\infty }$, has a convergent subsequence, where (PS) means Palais-Smale.

Lemma 4.1 (see [16])

Let X be a Banach space, $\phi \in C^1(X,\mathbb{R})$, $e\in X$ and $r>0$ be such that $\parallel e\parallel >r$ and

$$b:=\underset{\parallel u\parallel =r}{inf}\phi (u)>\phi (0)\ge \phi (e).$$

If φ satisfies the (PS) _c condition with

then c is a critical value of φ.

The main results are the following.

Theorem 4.1 Suppose that f satisfies the condition either

• (i) $f(x,0)\not\equiv 0$ in Ω, or

• (ii) $f(x,0)\equiv 0$ and there are an open set $U\subset \mathrm{\Omega }$, a closed ball $\overline{B}(x_0,\rho )\subset U$, some positive constants $r_0>1$ and $c_3$ such that $f(x,t)\ge c_3{t}^{r_0-1}$ for $x\in \overline{B}(x_0,\rho )$ and $t\in [0,1]$, and $r_0<p(x)$ for $x\in \partial U$.

Then we have the following assertions:

• (1) For sufficiently small $\lambda >0$, (4.1) has a solution $u_{\lambda }$ which is a local minimizer of $J_{\lambda }$ in the $C^1$ topology. Moreover, ${\parallel u_{\lambda }\parallel }_{C^1(\overline{\mathrm{\Omega }})}\to 0$ as $\lambda \to 0$.

• (2) Define ${\mathrm{\Lambda }}_0=\{\lambda >0:\text{ (4.1) }\mathit{\text{has a solution}}{u}_{\lambda }\mathit{\text{which is a local minimizer of}}{J}_{\lambda }\mathit{\text{in}}\mathit{\text{the}}{C}^1\mathit{\text{topology}}\}$ and $\mathrm{\Lambda }=\{\lambda >0:\text{ (4.1) }\mathit{\text{has a solution}}{u}_{\lambda }\}$. Then ${\mathrm{\Lambda }}_0$ and Λ are both intervals, $inf{\mathrm{\Lambda }}_0=inf\mathrm{\Lambda }=0$ and ${\mathrm{\Lambda }}_0\supset int\mathrm{\Lambda }$.

• (3) In addition, suppose that $\mu >0$, $q(x)<p^{\ast }(x)$ for $x\in \overline{\mathrm{\Omega }}$ and

  $$|f(x,t)|\le c(1+{|t|}^{r(x)})\mathit{\text{for}}x\in \mathrm{\Omega }\mathit{\text{and}}t\in \mathbb{R},$$

where $r(x)<p^{\ast }(x)$ for $x\in \overline{\mathrm{\Omega }}$ and $r^{+}<q^{-}$. Then for each $\lambda \in int\mathrm{\Lambda }$, (4.1) has at least two solutions $u_{\lambda }$ and $v_{\lambda }$ such that $u_{\lambda }<v_{\lambda }$ and $u_{\lambda }$ is a local minimizer of $J_{\lambda }$ in the $W^{1,p(x)}$ topology.

Proof (1) Take $0<\mathcal{M}<h$, where h is as in Lemma 2.1, and let $v=v_{\mathcal{M}}$ be the unique positive solution of (2.4). Then by Lemma 2.1, ${|v|}_{\mathrm{\infty }}\le C_{\ast }{\mathcal{M}}^{1/(p^{+}-1)}$. Because $q^{-}>p+$, we can choose ℳ small enough such that $\mu {(C_{\ast }{M}^{1/(p^{+}-1)})}^{q^{-}-1}<\frac{\mathcal{M}}{2}$, which implies that $\mu v^{q(x)-1}<\frac{\mathcal{M}}{2}$. Let $\lambda >0$ be sufficiently small such that $\lambda f(x,v)<\frac{\mathcal{M}}{2}$. Then for such λ,

$$-M(I(v)){\mathrm{\Delta }}_{p(x)}v=\mathcal{M}>\lambda f(x,v)+\mu {|v|}^{q(x)-2}v,$$

which shows that v is a supersolution of (4.1) and is not a solution of (4.1). By Theorem 3.2, $v>0$ in Ω and $\frac{\partial v}{\partial \mathbf{n}}>0$ on ∂ Ω.

In the case when f satisfies the condition (i), 0 is a subsolution of (4.1) and 0 does not satisfy the equation in (4.1). Moreover, by Theorem 3.4, (4.1) has a solution $u_{\lambda }\in [0,v]\cap C^1(\overline{\mathrm{\Omega }})$, which is a local minimizer of $J_{\lambda }$ in the $C^1$ topology.

In the case when f satisfies the condition (ii), 0 satisfies the equation in (4.1). We claim that 0 is not a minimizer of $J_{\lambda }$ on $[0,v]\cap X$. To see this, noting $J_{\lambda }(0)=0$, it is sufficient to show that ${inf}_{[0,v]\cap X}{J}_{\lambda }(u)<0$. For $\delta >0$, denote $U_{\delta }=\{x\in U:dist(x,\partial U)<\delta \}$. By the condition (ii), we can find sufficiently small positive constants ρ such that $\overline{B}(x_0,\rho )\subset U\setminus U_{\delta }$, $r_0<p^{-}(U_{\delta }):=inf\{p(x):x\in U_{\delta }\}$. Define a function $w\in C_0^{\mathrm{\infty }}(U)$ such that $0\le w\le 1$ and $w=1$ on $U\setminus U_{\delta }$. Then for sufficiently small $1>t>0$, we have that $tw\in [0,v]$ and

$$\begin{array}{rcl}{J}_{\lambda }(tw)& \le & \hat{M}\left({\int }_{U_{\delta }}\frac{t^{p(x)}}{p(x)}{|\mathrm{\nabla }w|}^{p(x)}dx\right)-\lambda {\int }_{U\setminus U_{\delta }}F(x,tw)dx\\ \le & M\left({\int }_{U_{\delta }}\frac{t^{p(x)}}{p(x)}{|\mathrm{\nabla }w|}^{p(x)}dx\right){\int }_{U_{\delta }}\frac{t^{p(x)}}{p(x)}{|\mathrm{\nabla }w|}^{p(x)}dx-\lambda {\int }_{U\setminus U_{\delta }}F(x,tw)dx\\ \le & t^{p^{-}(U_{\delta })}M\left({\int }_{U_{\delta }}\frac{1}{p(x)}{|\mathrm{\nabla }w|}^{p(x)}dx\right){\int }_{U_{\delta }}\frac{1}{p(x)}{|\mathrm{\nabla }w|}^{p(x)}dx-c_1\lambda t^{r_0}{\int }_{U\setminus U_{\delta }}{w}^{r_0}dx\\ <& 0,\end{array}$$

which shows that the claim is true. By Theorem 3.4, there exists $u_{\lambda }\in [0,v]\cap C^{1,\alpha }(\overline{\mathrm{\Omega }})$ such that $J_{\lambda }(u_{\lambda })={inf}_{[0,v]\cap X}{J}_{\lambda }(u)$, $u_{\lambda }$ is a solution of (4.1) and $u_{\lambda }$ is a local minimizer of $J_{\lambda }$ in the $C^1$ topology.

When $\lambda \to 0$, we can take $\mathcal{M}\to 0$, consequently ${|v_{\mathcal{M}}|}_{\mathrm{\infty }}\to 0$ and ${|u_{\lambda }|}_{\mathrm{\infty }}\to 0$. Furthermore, ${\parallel v_{\mathcal{M}}\parallel }_X\to 0$ and ${\parallel v_{\mathcal{M}}\parallel }_{C^1(\overline{\mathrm{\Omega }})}\to 0$. Assertion (1) is proved.

(2) The proof is similar to the proof of [3], we omit it here (for details, see the proof of Theorem 4.1 in [3]).

• (3) Note that, under additional assumptions, it is easy to verify that $J_{\lambda }\in C^1(X,\mathbb{R})$ and $J_{\lambda }$ satisfies the (PS) _c condition for all λ. Now let $\lambda \in int\mathrm{\Lambda }\subset {\mathrm{\Lambda }}_0$ be given arbitrarily. Take ${\lambda }_1,{\lambda }_2\in {\mathrm{\Lambda }}_0$ with ${\lambda }_2<\lambda <{\lambda }_1$, and let $u_{{\lambda }_1}$, $u_{\lambda }$ and $u_{{\lambda }_2}$ be the solutions of (4.1), (4.1 _λ ) and (4.1) respectively, $u_{{\lambda }_2}\le u_{\lambda }\le u_{{\lambda }_1}$, and let $u_{\lambda }$ be a local minimizer of $J_{\lambda }$ in the $C^1$ topology. Then by Theorem 3.1, $u_{\lambda }$ is also a local minimizer of $J_{\lambda }$ in the $W^{1,p(x)}$ topology. Define

  

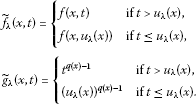
Consider the problem

$$\{\begin{array}{c}-M({\int }_{\mathrm{\Omega }}\frac{1}{p(x)}{|\mathrm{\nabla }u|}^{p(x)}dx)div({|\mathrm{\nabla }u|}^{p(x)-2}\mathrm{\nabla }u)=\lambda {\tilde{f}}_{\lambda }(x,u)+\mu {\tilde{g}}_{\lambda }(x,u)\text{in }\mathrm{\Omega },\hfill \\ u>0\text{in }\mathrm{\Omega },u=0\text{on }\partial \mathrm{\Omega },\hfill \end{array}$$

(4.2)

and denote the associated functional to (4.2) by ${\tilde{J}}_{\lambda }$. It is easy to see that $u_{{\lambda }_2}$ and $u_{{\lambda }_1}$ are a subsolution and a supersolution of (4.2), respectively. By Theorem 3.4, there exists $u_{\lambda }^{\ast }\in [u_{{\lambda }_2},u_{{\lambda }_1}]\cap C^1(\overline{\mathrm{\Omega }})$ such that $u_{\lambda }^{\ast }$ is a solution of (4.2) and is a local minimizer of ${\tilde{J}}_{\lambda }$ in the $C^1$ topology. By Theorem 2.2(1), we can see that $u_{\lambda }^{\ast }\ge u_{\lambda }$ and consequently $u_{\lambda }^{\ast }$ is also a solution of (4.1 _λ ). If $u_{\lambda }^{\ast }\ne u_{\lambda }$, then assertion (3) already holds, hence we can assume that $u_{\lambda }^{\ast }=u_{\lambda }$. Now $u_{\lambda }$ is a local minimizer of ${\tilde{J}}_{\lambda }$ in the $C^1$ topology, and so also in the $W^{1,p(x)}$ topology. We can assume that $u_{\lambda }$ is a strictly local minimizer of ${\tilde{J}}_{\lambda }$ in the $W^{1,p(x)}$ topology, otherwise we have obtained assertion (3). It is easy to verify that, under the additional assumptions in the statement (3), ${\tilde{J}}_{\lambda }\in C^1(X,\mathbb{R})$ and ${\tilde{J}}_{\lambda }$ satisfies the (PS) _c condition. From $q^{-}>p^{+}$, ($M_0$) and $\mu >0$, it follows that $inf\{{\tilde{J}}_{\lambda }(u):u\in X\}=-\mathrm{\infty }$. Using Lemma 4.1, we know that (4.2) has a solution $v_{\lambda }$ such that $v_{\lambda }\ne u_{\lambda }$, as a solution of (4.2), $v_{\lambda }$ must satisfy $v_{\lambda }\ge u_{\lambda }$, and consequently, by Theorem 3.2 and Theorem 3.3, $v_{\lambda }>u_{\lambda }$. Noting that $v_{\lambda }$ is also a solution of (4.1 _λ ) since $v_{\lambda }\ge u_{\lambda }$, thus the proof of assertion (3) is complete. □

Note that in the case of Theorem 4.1(1) and (2), the variational method cannot be used directly because we do not suppose that $q(x)\le p^{\ast }(x)$ and do not restrict the growth rate of f.