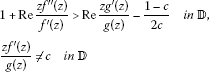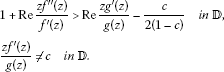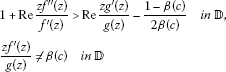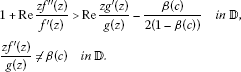Some properties concerning close-to-convexity of certain analytic functions

Abstract

Let $f(z)$ be an analytic function in the open unit disk $\mathbb{D}$ normalized with $f(0)=0$ and $f^{\prime }(0)=1$. With the help of subordinations, for convex functions $f(z)$ in $\mathbb{D}$, the order of close-to-convexity for $f(z)$ is discussed with some example.

MSC:30C45.

1 Introduction

Let $\mathcal{A}$ be the class of functions $f(z)$ of the form

$$f(z)=z+\sum _{n=2}^{\mathrm{\infty }}{a}_n{z}^n$$

which are analytic in the open unit disk $\mathbb{D}=\{z\in \mathbb{C}||z|<1\}$. A function $f(z)\in \mathcal{A}$ is said to be convex of order α if it satisfies

$$1+Re\frac{z{f}^{″}(z)}{f^{\prime }(z)}>\alpha \text{in }\mathbb{D}$$

for some real α ($0\leqq \alpha <1$). This family of functions was introduced by Robertson [1] and we denote it by $\mathcal{K}(\alpha )$.

A function $f(z)\in \mathcal{A}$ is called starlike of order α in $\mathbb{D}$ if it satisfies

$$Re\frac{z{f}^{\prime }(z)}{f(z)}>\alpha \text{in }\mathbb{D}$$

for some real α ($0\leqq \alpha <1$).

This class was also introduced by Robertson [1] and we denote it by ${\mathcal{S}}^{\ast }(\alpha )$. By the definitions for the classes $\mathcal{K}(\alpha )$ and ${\mathcal{S}}^{\ast }(\alpha )$, we know that $f(z)\in \mathcal{K}(\alpha )$ if and only if $z{f}^{\prime }(z)\in {\mathcal{S}}^{\ast }(\alpha )$.

Marx [2] and Strohhäcker [3] showed that $f(z)\in \mathcal{K}(0)$ implies $f(z)\in {\mathcal{S}}^{\ast }(\frac{1}{2})$.

This estimate is sharp for an extremal function

$$f(z)=\frac{z}{1-z}.$$

Jack [4] posed a more general problem: What is the largest number $\beta =\beta (\alpha )$ so that

$$\mathcal{K}(\alpha )\subset {\mathcal{S}}^{\ast }(\beta (\alpha )).$$

MacGregor [5] determined the exact value of $\beta (\alpha )$ for each α ($0\leqq \alpha <1$) as the infimum over the disc $\mathbb{D}$ of the real part of a specific analytic function. It has been conjectured that this infimum is attained on the boundary of $\mathbb{D}$ at $z=-1$.

Wilken and Feng [6] asserted MacGregor’s conjecture: If $0\leqq \alpha <1$ and $f(z)\in \mathcal{K}(\alpha )$, then $f(z)\in {\mathcal{S}}^{\ast }(\beta (\alpha ))$, where

$$\beta (\alpha )=\{\begin{array}{cc}\frac{1-2\alpha }{2^{2(1-\alpha )}-2}\hfill & \text{if }\alpha \ne \frac{1}{2},\hfill \\ \frac{1}{2log2}\hfill & \text{if }\alpha =\frac{1}{2}.\hfill \end{array}$$

(1)

Ozaki [7] and Kaplan [8] investigated the following functions: If $f(z)\in \mathcal{A}$ satisfies

$$Re\frac{f^{\prime }(z)}{g^{\prime }(z)}>0\text{in }\mathbb{D}$$

for some convex function $g(z)$, then $f(z)$ is univalent in $\mathbb{D}$. In view of Kaplan [8], we say that $f(z)$ satisfying the above inequality is close-to-convex in $\mathbb{D}$.

It is well known that the above definition concerning close-to-convex functions is equivalent to the following condition:

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>0\text{in }\mathbb{D}$$

for some starlike function $g(z)\in \mathcal{A}$.

Let us define a function $f(z)\in \mathcal{A}$ which satisfies

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>\alpha \text{in }\mathbb{D}$$

for some real α ($0\leqq \alpha <1$) and for some starlike function $g(z)$ in $\mathbb{D}$.

Then we call $f(z)$ close-to-convex of order α in $\mathbb{D}$ with respect to $g(z)$.

It is the purpose of the present paper to investigate the order of close-to-convexity of the functions which satisfy $f(z)\in \mathcal{K}(\alpha )$ and $0\leqq \alpha <1$.

2 Preliminary

To discuss our problems, we have to give here the following lemmas.

Lemma 1 Let $p(z)=1+{\sum }_{n=1}^{\mathrm{\infty }}{c}_n{z}^n$ be analytic in $\mathbb{D}$ and suppose that

$$p(z)\prec \frac{1-\alpha z}{1+\beta z}\mathit{\text{in}}\mathbb{D},$$

where ≺ means the subordination, $0<\alpha <1$ and $0<\beta <1$.

Then we have

$$\frac{1-\alpha }{1+\beta }<Rep(z)<\frac{1+\alpha }{1-\beta }.$$

This shows that

$$Rep(z)>0\mathit{\text{in}}\mathbb{D}.$$

A proof is very easily obtained.

Lemma 2 Let $p(z)=1+{\sum }_{n=1}^{\mathrm{\infty }}{c}_n{z}^n$ be analytic in $\mathbb{D}$, and suppose that there exists a point $z_0\in \mathbb{D}$ such that

$$Rep(z)>c\mathit{\text{for}}|z|<|z_0|$$

and

$$Rep(z_0)=c,p(z_0)\ne c$$

for some real c ($0<c<1$). Then we have

$$Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}\leqq \{\begin{array}{cc}-\frac{1-c}{2c}\hfill & \mathit{\text{when}}\frac{1}{2}\leqq c<1,\hfill \\ -\frac{c}{2(1-c)}\hfill & \mathit{\text{when}}0<c<\frac{1}{2}.\hfill \end{array}$$

Proof Let us put

$$q(z)=\frac{p(z)-c}{1-c},q(0)=1.$$

Then $q(z)$ is analytic in $\mathbb{D}$ and

$$Req(z)>0\text{for }|z|<|z_0|$$

and

$$Req(z_0)=0,q(z_0)\ne 0.$$

Then, from [[9], Theorem 1], we have

$$\frac{z_0{q}^{\prime }(z_0)}{q(z_0)}=i\ell ,$$

where

$$\ell \geqq \frac{1}{2}(a+\frac{1}{a})\geqq 1\text{when }argq(z_0)=\frac{\pi }{2}$$

and

$$\ell \leqq -\frac{1}{2}(a+\frac{1}{a})\leqq -1\text{when}argq(z_0)=-\frac{\pi }{2},$$

where $q(z_0)=\pm ia$ and $a>0$.

For the case $argq(z_0)=\frac{\pi }{2}$, we have

$$\frac{z_0{q}^{\prime }(z_0)}{q(z_0)}=\frac{z_0{p}^{\prime }(z_0)}{p(z_0)-c}=i\ell$$

and so

If we put

$$h(x)=\frac{1+x^2}{c^2+{(1-c)}^2{x}^2}(x>0),$$

then it is easy to see that

$$\frac{1}{c^2}<h(x)<\frac{1}{{(1-c)}^2}\text{when }\frac{1}{2}\leqq c<1$$

and

$$\frac{1}{{(1-c)}^2}<h(x)<\frac{1}{c^2}\text{when }0<c<\frac{1}{2}.$$

This shows that

$$Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}\leqq \{\begin{array}{cc}-\frac{1-c}{2c}\hfill & \text{when }\frac{1}{2}\leqq c<1,\hfill \\ -\frac{c}{2(1-c)}\hfill & \text{when }0<c<\frac{1}{2}.\hfill \end{array}$$

For the case $argq(z_0)=-\frac{\pi }{2}$, applying the same method as above, we have the same conclusion

$$Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}\leqq \{\begin{array}{cc}-\frac{1-c}{2c}\hfill & \text{when }\frac{1}{2}\leqq c<1,\hfill \\ -\frac{c}{2(1-c)}\hfill & \text{when }0<c<\frac{1}{2}.\hfill \end{array}$$

This completes the proof of the lemma. □

Our next lemma is

Lemma 3 Let $p(z)=1+{\sum }_{n=1}^{\mathrm{\infty }}{c}_n{z}^n$ be analytic in $\mathbb{D}$ and suppose that there exists a point $z_0\in \mathbb{D}$ such that

$$Rep(z)>c\mathit{\text{for}}|z|<|z_0|$$

and

$$Rep(z_0)=c,p(z_0)\ne c$$

for some real c ($c<0$).

Then we have

$$Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}>-\frac{c}{2(1-c)}>0.$$

(2)

Proof Let us put

$$q(z)=\frac{p(z)-c}{1-c},q(0)=1.$$

Then $q(z)$ is analytic in $\mathbb{D}$. If $p(z)$ satisfies the hypothesis of the lemma, then there exists a point $z_0\in \mathbb{D}$ such that

$$Req(z)>0\text{for }|z|<|z_0|$$

and

$$Req(z_0)=0\text{and}q(z_0)\ne 0,$$

then $p(z)$ satisfies the conditions of the lemma.

For the case $argq(z_0)=\frac{\pi }{2}$, applying the same method as in the proof of Lemma 2, we have

$$Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}=-\frac{(1-c)ca\ell }{c^2+{(1-c)}^2{a}^2}\geqq -\frac{c(1-c)}{2}\left(\frac{1+a^2}{c^2+{(1-c)}^2{a}^2}\right).$$

Putting

$$h(x)=\frac{1+x^2}{c^2+{(1-c)}^2{x}^2}(x>0),$$

it follows that

$$h^{\prime }(x)=\frac{(2c-1)x}{{(c^2+{(1-c)}^2{x}^2)}^2}<0(x>0).$$

(3)

Therefore, from (3) we obtain (2) .

For the case $argq(z_0)=-\frac{\pi }{2}$, applying the same method as above, we have the same conclusion as in the case $argq(z_0)=\frac{\pi }{2}$. □

3 The order of close-to-convexity

Now, we discuss the close-to-convexity of $f(z)$ with the help of lemmas.

Theorem 1 Let $f(z)\in \mathcal{A}$, and suppose that there exists a starlike function $g(z)$ such that

• (i) for the case $\frac{1}{2}\leqq c<1$,

  

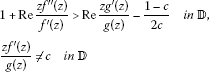
and

• (ii) for the case $0<c<\frac{1}{2}$,

  

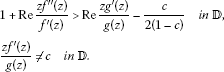
Then we have

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>c\mathit{\text{in}}\mathbb{D}.$$

This means that $f(z)$ is close-to-convex of order c in $\mathbb{D}$.

Proof Let us put

$$p(z)=\frac{z{f}^{\prime }(z)}{g(z)},p(0)=1.$$

Then it follows that

$$1+\frac{z{f}^{″}(z)}{f^{\prime }(z)}=\frac{z{g}^{\prime }(z)}{g(z)}+\frac{z{p}^{\prime }(z)}{p(z)}.$$

• (i) For the case $\frac{1}{2}\leqq c<1$, if there exists a point $z_0\in \mathbb{D}$ such that

  $$Rep(z)>c\text{for }|z|<|z_0|$$

and

$$Rep(z_0)=c,$$

then, applying Lemma 2 and the hypothesis of Theorem 1, we have

$$p(z_0)\ne c$$

and

$$Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}\leqq -\frac{1-c}{2c}.$$

Thus, it follows that

$$\begin{array}{rcl}1+Re\frac{z_0{f}^{″}(z_0)}{f^{\prime }(z_0)}& =& Re\frac{z_0{g}^{\prime }(z_0)}{g(z_0)}+Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}\\ \leqq & Re\frac{z_0{g}^{\prime }(z_0)}{g(z_0)}-\frac{1-c}{2c},\end{array}$$

which contradicts the hypothesis of Theorem 1. (ii) For the case $0<c<\frac{1}{2}$, applying the same method as above, we also have that

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>c\text{in }\mathbb{D}.$$

This completes the proof of the theorem. □

Applying Theorem 1, we have the following corollary.

Corollary 1 Let $f(z)\in \mathcal{A}$ be convex of order α ($0<\alpha <1$), and suppose that there exists a starlike function $g(z)$ such that

• (i) for the case $\frac{1}{2}\leqq \alpha <c$,

  

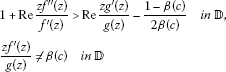
and

• (ii) for the case $0<\alpha <c\leqq \frac{1}{2}$,

  

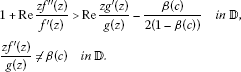
Then we have

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>\beta (c)>\beta (\alpha )>\alpha \mathit{\text{in}}\mathbb{D}.$$

Remark 1 For the case $0<\alpha <c<1$, it is trivial that

$$\alpha <\beta (\alpha )<\beta (c)<1.$$

Example 1 Let $f(z)\in \mathcal{A}$ satisfy

$$1+Re\frac{z{f}^{″}(z)}{f^{\prime }(z)}>Re\frac{1-Az}{1+Az}-\frac{1-\beta (\frac{1}{2})}{2\beta (\frac{1}{2})}>-\frac{1}{10}\text{in }\mathbb{D},$$

(4)

where

$$A=\frac{32\beta (\frac{1}{2})-10}{8\beta (\frac{1}{2})+10}\fallingdotseq 0.29605$$

and $\beta (\frac{1}{2})=\frac{1}{2log2}$. If we consider the starlike function $g(z)$ given by

$$g(z)=\frac{z}{{(1+Az)}^2},$$

then we have

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>\beta \left(\frac{1}{2}\right)\fallingdotseq 0.7213,$$

which means that $f(z)$ is close-to-convex of order $\beta (\frac{1}{2})$ in $\mathbb{D}$.

Next we show

Theorem 2 Let $f(z)\in \mathcal{A}$ and $g(z)\in \mathcal{A}$ be given by

$$g(z)=\{\begin{array}{cc}\frac{z}{{(1+\beta z)}^{\frac{\alpha +\beta }{\beta }}}\hfill & (\beta \ne 0),\hfill \\ z{e}^{-\alpha z}\hfill & (\beta =0)\hfill \end{array}$$

for some α ($0\leqq \alpha <1$) and some β ($0\leqq \beta <1$). Further suppose that for arbitrary r ($0<r<1$),

$$\underset{|z|=r}{min}(Re\frac{z{f}^{\prime }(z)}{g(z)})={(Re\frac{z_0{f}^{\prime }(z_0)}{g(z_0)})}_{|z_0|=r}\ne \frac{z_0{f}^{\prime }(z_0)}{g(z_0)}$$

and

$$1+Re\frac{z{f}^{″}(z)}{f^{\prime }(z)}\leqq -\frac{c}{2(1-c)}+\frac{1-\alpha }{1+\beta }$$

for $c<0$. Then we have

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>c\mathit{\text{in}}\mathbb{D}.$$

Proof Let us define the function $p(z)$ by

$$p(z)=\frac{z{f}^{\prime }(z)}{g(z)},p(0)=1$$

for $c<0$. If there exists a point $z_0\in \mathbb{D}$ such that

$$Rep(z)>c\text{for }|z|<|z_0|$$

and

$$Rep(z_0)=c$$

for $c<0$, then from the hypothesis of Theorem 2, we have

$$Rep(z_0)\ne p(z_0).$$

Therefore, applying Lemma 1 and Lemma 3, we have

$$\begin{array}{rcl}1+Re\frac{z_0{f}^{″}(z_0)}{f^{\prime }(z_0)}& =& Re\frac{z_0{p}^{\prime }(z_0)}{p(z_0)}+Re\frac{z_0{g}^{\prime }(z_0)}{g(z_0)}\\ >& -\frac{c}{2(1-c)}+\frac{1-\alpha }{1+\beta }.\end{array}$$

This is a contradiction, and therefore we have

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>c\text{in }\mathbb{D}.$$

 □

Remark 2 In view of the definition for close-to-convex functions, if $f(z)$ satisfies

$$Re\frac{z{f}^{\prime }(z)}{g(z)}>0\text{in }\mathbb{D},$$

then we can say that $f(z)$ is close-to-convex in $\mathbb{D}$. But c should be a negative real number in Theorem 2. Therefore, we cannot say that $f(z)$ is close-to-convex in $\mathbb{D}$ in Theorem 2.