- Research
- Open access
- Published:
On finite groups with their character tables having at most zeros in each column
Journal of Inequalities and Applications volume 2012, Article number: 152 (2012)
Abstract
In the present paper, the authors classify finite solvable groups whose character tables have at most zeros in each column, where p is the minimal prime divisor of their orders.
MSC:20C15.
1 Introduction
The distribution of zeros in the character table of a group is a classical problem with an extensive literature that goes back to the well-known theorem of Burnside stating that any non-linear irreducible character of a finite group vanishes at some element of the group. Hence it is interesting to investigate the properties of a finite group with ‘many’ zeros or without zeros at some special places in its character table. There are many results about the number of zeros in the rows of a character table (see [2, 3, 6, 17] and [7], etc.).
On the other hand, we find that it is also interesting to study the distribution of zeros in terms of a column. Isaacs et al. [5] investigated the property of an element x of odd order such that every irreducible character does not take zero on x, and proved that such element x was contained in the Fitting subgroup. Hence the number of zeros in the columns of a character table will have effect on the group structure. Xu et al. [13] classified finite groups of odd order with their character tables having at most p zeros on each column, where p is the smallest prime divisor of the group order. In this paper, we classify finite solvable groups with their character tables having at most zeros in each column, where p is the minimal prime divisor of their orders.
Definition 1.1 A group is called -group if its character table has at most k zeros in each column.
Definition 1.2 Let be a character, and A be a subset of G. For , if , we say θ vanishes at x. If for any , we say that θ vanishes on A.
All further unexplained symbols and notation are standard and can be found, for instance, in [4]. In particular, denotes an elementary abelian group of order .
In this paper, we study solvable -groups, where p is a minimal prime divisor of . Hence there are two cases that need to be considered: and .
For , we have the following theorem.
Theorem A Let G be solvable such that. Then G is a-group if and only if one of the following holds:
-
(1)
G has exactly one non-linear irreducible character;
-
(2)
G has exactly two non-linear irreducible characters;
-
(3)
G has exactly three non-linear irreducible characters;
-
(4)
G has a normal series, where, , , and;
-
(5)
, whereis a Frobenius group;
-
(6)
, whereis a Frobenius group, and the action of G on the setis non-trivial;
-
(7)
, where;
-
(8)
, whereis a Frobenius group;
-
(9)
G is abelian.
For, then G is an odd order by the minimality of p, and G must be solvable. And we get:
Theorem B Let G be a finite group and p be the minimal odd prime divisor of its order. Then G is a-group if and only if one of the following holds:
-
(i)
G is abelian;
-
(ii)
G is an extra-special p-group;
-
(iii)
is a Frobenius group with an elementary abelian kerneland a cyclic complement L, and.
2 Preliminaries
In this section, we give some results which will be applied to our further investigations.
Lemma 2.1 ([12], Theorem 1])
Let G be a solvable finite group. Then the character table of G has at most one zero in each column if and only if one of the following holds:
-
(1)
G is abelian;
-
(2)
G has exactly one non-linear irreducible character, and one of the following holds:
(2.1) G is an extra-special 2-group;
(2.2) is a Frobenius group with a kernel N and a complement H, where H is an abelian group and N is an elementary abelian p-group such that.
Lemma 2.2 ([1], Theorem B])
Let x be an element in a p-group P with. Then there exist at leastnon-linear irreducible characters vanishing at x.
Lemma 2.3 ([8], Proposition 3.2.2])
Let G be a solvable group. Assume that G has at most two irreducible characters of degree m (≠1). If, then one of the following occurs:
-
(1)
;
-
(2)
is a Frobenius group with a kerneland a complement;
-
(3)
.
If, G is π-nilpotent and a normal π-complement of G is non-abelian, where, then one of the following occurs:
-
(i)
is a Frobenius group with a kernel K of order 25 and a complement H, where K is an elementary abelian group and H is a dihedral group;
-
(ii)
is a Frobenius group with an elementary abelian kernel K of order 81 and a complement A, whereand;
-
(iii)
, where A is a cyclic subgroup of order 4 and B is an extra-special group of order 27;
-
(iv)
G is the normalizer of a Sylow 2-group of the simple group.
Lemma 2.4 ([14])
Let G be a finite group and. Then G is a Frobenius group with a kernel N if and only ifis irreducible for anyand.
Lemma 2.5 ([10])
A finite solvable group G has exactly one non-linear irreducible character if and only if one of the following holds:
-
(1)
G is an extra-special 2-group;
-
(2)
is a Frobenius group with an elementary abelian kernel N and an abelian complement H such that.
Lemma 2.6 ([15], Theorem 2])
A finite solvable group G has exactly two non-linear irreducible characters if and only if one of the following holds:
-
(1)
G is an extra-special 3-group;
-
(2)
is a Frobenius group with an elementary abelian kernel N and an abelian complement H such that;
-
(3)
is a Frobenius group with a Frobenius complement;
-
(4)
G is an 2-group of class 3, and G has a normal seriessatisfying the conditions: is an extra special 2-group, and;
-
(5)
G is an 2-group of class 2, and G has a normal seriessatisfying the conditions: is an elementary abelian group, and;
-
(6)
is a Frobenius group with an elementary abelian kernel N and an abelian complement H such that. Furthermore, and.
Lemma 2.7 ([9], Corollary 1])
Let G be a non-abelian group of odd order and p be the minimal prime divisor of. Then G has at most 2p irreducible characters of degree m whereif and only if one of the following occurs:
-
(1)
G is an extra-special p-group;
-
(2)
is a Frobenius group with an elementary abelian kernel K and a cyclic complement H. Moreover, .
Lemma 2.8 ([16], Theorem 2.3])
Let G be non-nilpotent and, where q is a prime number. Thenif and only if one of the following assertions holds:
-
(1)
is abelian, , p is a prime divisor of
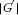 , is a prime number;
, is a prime number; -
(2)
, is an abelian p-group and A is cyclic, (q is a prime number), is a Frobenius group with a Frobenius kernel isomorphic toand a cyclic Frobenius complement of order;
-
(3)
, whereis a Frobenius group with an elementary abelian kernel N and a cyclic complement H such that. Moreover, , where q is a prime number;
-
(4)
G is a Frobenius group with an elementary abelian kernel N and a cyclic complement H such that, where q is a prime number.
3 Proof of Theorem A
To make the proof clear, we give the following lemma:
Lemma 3.1 Let G be a-group, andbe the inertia group of φ. There exists a subgroupsuch that. Moreover, for eachsuch that, there exists a unique, lying over ϕ and vanishing on. Hence there are at leastirreducible characters of G, lying over φ and vanishing on.
Proof By [11], Lemma 2.2], there exists such that φ is extendible to and ϕ and φ are fully ramified with respect to .
Note for . Applying Clifford theory, we see that there exists a unique such that and χ vanishes on .
Suppose ϕ vanishes at x. So is λϕ for each . Note that φ is also extendible to . Since G is a -group, . □
In practice, we always choose as big as possible.
Proof of Theorem A Obviously, we need only to show the necessity.
Since an abelian group is obviously a -group, so we may assume that G is a non-abelian solvable group. We divide the proof into 3 cases by the order of .
Case 1. If , we claim that G is one of the groups in (1), (2) and (3).
Let φ be a non-linear irreducible character of . If φ is extendible to an irreducible character , then the irreducible characters of the form λχ for are distinct irreducible characters of G by [4], Theorem 6.17], which vanish at the elements as φ. Hence , a contradiction. For each non-principle character , by Lemma 3.1, there exists such that . Now we consider the action of G on the set of by for and .
Subcase 1.1. The action of G on has at least four orbits.
Let () be non-principal irreducible characters of from four different orbits. By Lemma 3.1, there exists such that . Then vanishes on , , which implies . Since , . If , then , where . By Lemma 3.1, for each i, there are exactly three irreducible characters , and of G, lying over and vanishing on . Since is proper in G, for . Let . Then there are six irreducible characters of G vanishing at x, which is a contradiction. Similarly, we also get a contradiction if .
Subcase 1.2. The action of G on has exactly three orbits.
Let () be non-principal irreducible characters from different orbits. If satisfies , then, by Lemma 3.1, there are at least four irreducible characters of G, lying over , or and vanishing on , which implies for G is a -group. Since , there are at least two of these irreducible characters , satisfying . By Lemma 3.1, there are at least four irreducible characters of G, vanishing at an element, a contradiction. Hence for , which implies that G has exactly 3 non-linear irreducible characters.
Subcase 1.3. The action of G on has exactly two orbits.
We can choose two irreducible characters of , say and , from two different orbits respectively. If one of and , for example, satisfies , then there are at least four irreducible characters of G lying over and and vanishing on . Since G is a -group, it follows that . Hence, , which is clearly impossible since . If and satisfy , where , then there are at least four non-linear irreducible characters of G lying over and and vanishing on , which implies . Hence, , a contradiction. Therefore, there is at most one of the two irreducible characters and satisfying , which implies that G has at most 3 non-linear irreducible characters. Hence, G can only be isomorphic to one of the groups listed in (1), (2) or (3) by Lemma 2.5.
Subcase 1.4. The action of G on has exactly one orbit.
Since , G has at most three non-linear irreducible characters. By Lemma 2.5, it is easy to see that G is isomorphic to one of the groups listed in (1), (2) or (3).
Case 2. . Then G is one of the groups listed in conclusion (1)-(6).
Let χ be a non-principle irreducible character of G and θ an irreducible constituent of . In this case, we have that or . If , then χ vanishes on , which implies that G has at most three non-linear irreducible characters induced by those of .
Subcase 2.1. G has exactly one irreducible character, say β, induced from an irreducible characters of , say λ.
We have seen that . There are exactly three linear characters in . Using Lemma 3.1, there exists at most one zero in each column of the character table of . By Lemma 2.1, is abelian or has exactly one non-linear irreducible character. If is a non-abelian group, let φ be the unique non-linear irreducible character of and , where . Then G has exactly three non-linear irreducible characters χ, ξχ and , where . Clearly, . If , then , and , contrary to G is non-abelian. Therefore, . By Lemma 2.3, , and G is in (3). If is abelian, then . Hence and , and G is in (1).
Subcase 2.2. G has exactly two irreducible characters induced from irreducible characters of . Let β, α be the two irreducible characters such that and , where and .
Subsubcase 2.2.1. If λ and μ are linear, then G is a group as in the conclusion (2).
In the case has five linear characters (), and all non-linear irreducible characters of are extendible to G. By the same arguments as above, one has that there is at most one zero in each column of the character table of . By Lemma 2.1, we have that either is abelian or has exactly one non-linear irreducible character.
If is abelian, then G has exactly two non-linear irreducible characters. Hence, G is isomorphic to the group listed in (2) by Lemma 2.5.
If is a non-abelian group, let φ be the unique non-linear irreducible character of and , where . Then G has exactly four non-linear irreducible characters χ, ξχ, and , where . Since , it follows that . If , then . Hence, , which implies that is abelian, a contradiction. Therefore, , . So G satisfies the assumptions of Lemma 2.3. But it is easy to check by Lemma 2.3 that no such group exists.
Subsubcase 2.2.2. If either λ or μ is non-linear, then G is one of the groups in (2) and (4).
Without loss of generality, let and . In this case, one has that and =2, and so . Now, we assert that has at most two non-linear irreducible characters except μ and for each . Otherwise, we can choose three such irreducible characters of , say , and . We first assume that one of the three irreducible characters is extended by an irreducible character of . Let where . Since is extendible to G, we have that does not vanish for any element while vanishes if , which implies that μ, and are the three extensions of β, but and can not be extended by an irreducible character of . Let such that and . Then both and vanish on , a contradiction. In this case, the above assertion holds. Next, we assume that , and are not extended by an irreducible character of . Then each of them is induced by an irreducible character of , which implies that the irreducible characters , and vanish on , a contradiction.
Now, we have that has at most four non-linear irreducible characters. If has exactly two non-linear irreducible characters, then G has exactly two non-linear irreducible characters and , which concludes (2) in this case. Suppose has exactly three non-linear irreducible characters, say μ, and . By the same arguments as above, we have that either the irreducible characters μ, and can be extended by an irreducible character of or induced by an irreducible characters of . If μ, and are three extensions of an irreducible character of , then , which is impossible by Lemma 2.8. In the latter case, one has that is a Frobenius group with a kernel by Lemma 2.4. Furthermore, since and has exactly three non-linear irreducible characters, we get that is an abelian group. Hence , a contradiction to . Now, we have that has four irreducible characters, denoted by μ, , and . By the same argument as before, one has that μ, and are three extensions of an irreducible character of and , where . Since each linear character of is not extendible to , , which implies that has exactly four linear characters and one non-linear irreducible character. By Lemma 2.5, we have that , and so G has normal series , where , , , . Thus G is a group as in the conclusion (4).
Subcase 2.3. G has exactly three irreducible characters induced from irreducible characters of . Let , and be the three irreducible characters such that , and , where and .
Subsubcase 2.3.1. If λ, μ and η are linear characters, then G is one of the groups in (3) and (5).
In this case, one has that has seven linear characters () and all non-linear irreducible characters of are extendible to G. By the same arguments as before, we have that there are at most one zero in each column of the character table of . By Lemma 2.1, we have that either is abelian or has exactly one non-linear irreducible character.
If is abelian, then G has exactly three non-linear irreducible characters. In such case, (3) follows by Lemma 2.5.
If is non-abelian, then , where K is an elementary abelian group of order 8 and . Therefore, , and so (5) holds.
Subsubcase 2.3.2. If one of λ, μ or η is non-linear, then G is one of groups in (3) and (6).
Without loss of generality, let and . So . Take . If ξ is extendible to , then the irreducible characters of the form ρδ for any are all of the irreducible constituents of . Hence, one has that there are at least three irreducible characters of the set extendible to G, and the extensions have common zeros, a contradiction. Therefore, for every . Since vanish on , we have that has at most three non-linear irreducible characters. Otherwise, we can take four non-linear irreducible characters μ, , φ and ψ of , where . Clearly, φ and ψ are extendible to G. Moreover, we have four irreducible characters of G, two lying over φ and other two lying over ψ, vanishing on , a contradiction. By Lemma 2.4, is a Frobenius group with an abelian kernel . We know that and is an elementary abelian subgroup of order 16 or a cyclic subgroup of order 11. If , then G has exactly three irreducible characters , and . Hence (3) follows. If , then , where is a Frobenius group with an elementary abelian kernel of order 16 and a cyclic complement K of order 5; and the action of G on is non-trivial. In such case, (6) follows.
Subcase 2.3.3. If two of λ, μ and η are non-linear, then we claim that no such group exists.
Without loss of generality, let , and . In this case, . Let . Then either ξ is extendible to or . Moreover, we can get that any two irreducible characters of which are not μ, , η and for some have no common zeros. According to the properties of the distribution of zeros of G, we have that the non-linear irreducible characters of can only be one of the following two cases:
-
(a)
has 7 irreducible characters, μ, , η, , δ, θ and χ, where and such that and . On the other hand, μ, , η, are the four extensions of and while where and .
-
(b)
has 5 or 6 irreducible characters μ, , η, , δ and θ (maybe there exists no such θ), where such that , and . If there exists such an irreducible character θ of , then , where .
In the former case (a), one has that has only two non-linear irreducible characters with no common zeros, which is impossible by Lemma 2.1.
In the latter case (b), if , then , which implies that . Since ζ is a conjugate to ε in G, it follows that the quotient group isomorphic to a subgroup of or , a contradiction to . Hence, , and so . By Clifford theorem, it is easy to see that vanishes on . Let ω be an irreducible character of . Then . If , then ωξ is a conjugate to μ or η, and so ξ vanishes on some elements in , which implies that , and the two extensions of δ to G have common zeros in , a contradiction.
Case 3. . Then G is one of the groups in (1), (3) and (7).
Let χ be a non-principle irreducible character of G and θ be an irreducible constituent of . In this case, we have that or . If , then χ vanishes on , which implies that G has at most three irreducible characters induced from irreducible characters of .
Subcase 3.1. If G has exactly one irreducible character induced from irreducible characters of , then G is isomorphic to the group listed in (7) or , the alternating group of degree 4.
By the same arguments as in Subcase 2.1, one has that there exists at most one zero in each column of the character table of . By Lemma 2.1, is abelian or has exactly one non-linear irreducible character.
If is a non-abelian group, has exactly one irreducible non-linear character. Then and . By Lemma 2.5, . Moreover, we can get that . Hence, (7) holds.
If is an abelian group, then , and so . Hence, , (1) holds.
Subcase 3.2. G has exactly two irreducible characters induced from irreducible characters of . Let and be the two irreducible characters, where and .
Subsubcase 3.2.1. If λ and μ are linear characters, then G is one of the groups in (2) and (8).
In this case, we know that has seven linear characters since and all the non-linear irreducible characters of are extendible to G. By the same arguments as above, one has that there is at most one zero in each column of the character table of . By Lemma 2.1, we get that either is abelian or has exactly one non-linear irreducible character.
If is an abelian group, then G has exactly two non-linear irreducible characters. In the case (2) follows by Lemma 2.5.
If is a non-abelian group, then is a Frobenius group with an elementary abelian kernel of order 8 and a complement H of order 7. Thus , and so (8) holds.
Subsubcase 3.2.2. If one of λ and μ is non-linear, then there is no such group G.
Without loss of generality, let and . In this case, we have that and =3. Thus . We assert that has exactly three non-linear irreducible characters μ, and , where . Assume the contrary; let δ be an irreducible character of such that . According to the properties of the distribution of zeros of , it is easy to know that μ vanishes on and δ has zeros in . Hence, all of the three irreducible characters lying over δ and have common zeros, a contradiction. Therefore, G has exactly two non-linear irreducible characters and . Moreover, . But no such groups exist by Lemma 2.6, a contradiction.
Subcase 3.3. G has exactly three irreducible characters induced from irreducible characters of . Let , and be the three irreducible characters, where and .
Subsubcase 3.3.1. λ, μ and η are linear characters.
In this case, and , which is obviously impossible.
Subsubcase 3.3.2. One of λ, μ and η is non-linear.
Without loss of generality, let and . In this case, one has that . By the same arguments as in Subsubcase 2.3.2, for every , it follows that there necessarily exists an irreducible character such that . Hence, has exactly three non-linear irreducible characters μ, and , where . Then is a Frobenius group with an abelian kernel of order 22. But , which implies that is abelian, a contradiction.
Subsubcase 3.3.3. Two of λ, μ and η are non-linear.
Without loss of generality, let , and . In this case, we have that . By the same arguments as in Subsubcase 3.2.2, has exactly six non-linear irreducible characters μ, , , η, and , where . It follows that G has exactly three non-linear irreducible characters, and so (3) holds. This completes the proof of Theorem A. □
4 Proof of Theorem B
Let G be a -groups, where p is the minimal odd prime divisor of its order. Obviously, G is a solvable group since G is a group of odd order. In this section, we give the proof of Theorem B.
Proof of Theorem B If G is an abelian group, obviously G is a -group, and so we may assume that G is a non-abelian group. We divide the proof into two cases up to the order .
Case 1. .
Let φ be a non-linear irreducible character of . If φ is extendible to an irreducible character , then there are distinct irreducible characters of the form λχ of . Obviously, λχ vanishes at which φ vanishes. Hence . Since p is the minimal prime divisor , , a contradiction. Therefore, only the principal character of is extendible to an irreducible character of G.
For a non-principal character , by Lemma 3.1, exists and or p by the minimality of p. Now, consider the action of G on by for and .
Subcase 1.1. This action has at least orbits.
In this case, we can take irreducible characters of , say , from different orbits respectively. So can give rise to at least distinct irreducible characters of G and all of them vanish on , which implies . Since , . Hence, , where r is a prime and . If , then G has at least subgroups satisfying the equality , where . It follows that there are exactly p irreducible characters of G lying over and vanishing on for each i. Since , we have that the intersection is not empty for . Let x be an element of . Then there are 2p irreducible characters of G lying over , and vanishing at x, which leads to a contradiction. Now, we consider the case that . In this case, , where , and so the irreducible characters vanish on , an obvious contradiction. Therefore, there are at most orbits of the action of G on .
Subcase 1.2. This action has k orbits, where .
We can choose k irreducible characters of , say , lying in each of k different orbits respectively. If one of the k irreducible characters, for example, satisfies , then there are at least irreducible characters of G lying over and vanishing on , which forces . Hence , and then . But p is the minimal divisor of , a contradiction to . Therefore, we have that where , and hence G has at most non-linear irreducible characters. By Lemma 2.7, one has that either G is an extra special p-group or a Frobenius group with an elementary abelian kernel.
Let and . Since , we have that . It follows that , where . Hence, for each is divided by every prime divisor of . By [4], Theorem 12.2], G has a normal q-complement, and so G has a normal -complement. Let denote the normal q-complement of G, where q is a prime divisor of .
Subsubcase 1.2.1. If , then either G is an abelian group or an extra special p group. In the case that the desired conclusion (i) or (ii) holds.
Subsubcase 1.2.2. Suppose that and G is not nilpotent. In the following, we will show that is abelian for every prime divisor q of .
We first prove that if , then is an abelian group. Suppose is non-abelian. By Lemma 2.7, is an extra special group. So has non-linear irreducible characters, which implies that . Hence, one has that the action of on the set has at most 2 orbits. If is non-abelian, then the action of on the set has exactly one orbit. Thus, , which implies that is an even number, a contradiction. Hence, is an abelian group. Next, we assert that is the minimal normal subgroup of G. Assume the contrary. Let  and . Obviously, the action of G on the set has exactly one orbit. By the same reasoning as above, one has that is an even number, a contradiction; and so the assertion holds. Assume that is an elementary abelian q-group (). Till now, we get that G is a Frobenius group with a kernel and an extra-special complement of order . However, it is easy to check that no such group G exists, which leads to a contradiction.
and . Obviously, the action of G on the set has exactly one orbit. By the same reasoning as above, one has that is an even number, a contradiction; and so the assertion holds. Assume that is an elementary abelian q-group (). Till now, we get that G is a Frobenius group with a kernel and an extra-special complement of order . However, it is easy to check that no such group G exists, which leads to a contradiction.
Next, we prove that is an abelian group for . If is non-abelian, then has at least non-linear irreducible characters by Lemma 2.2. But G has at most non-linear irreducible characters, which implies that , a contradiction.
Set . Then K is a normal -complement of G and . Since G is solvable, we have that has a Hall- subgroup H. Obviously, H is a Hall- subgroup of G. In this case, one has that , and hence . Set and . Since , one has that λ is extendible to μ. Furthermore, λ is fully-ramified with respect to , which implies that . By Lemma 2.4, G is a Frobenius group with a kernel and a cyclic complement L. Since G has at most non-linear irreducible characters, one has that , where . Hence, (iii) holds.
Subcase 1.3. This action has at most two orbits.
If the action of G on has exactly one orbit, then is an even number, a contradiction. Now, we have that the action of G on the set has exactly two orbits. By the same reasoning as above, one has that is an abelian and a minimal normal subgroup of G. We can take two irreducible characters of , say and , from the two different orbits respectively. If both and satisfy , then there are 2p irreducible characters of G lying over and and vanishing on , which implies . But this is impossible since . If one of and , for example satisfies , then G has exactly non-linear irreducible characters. Moreover, we have is a Frobenius group with an elementary abelian kernel K and a cyclic complement H. Since is abelian, one has that . On the other hand, we know that , which implies that . Thus , a contradiction. Therefore, we have that , where . In the case that G has exactly two non-linear irreducible characters. By Lemma 2.6, one has that G is an extra special p-group, as desired.
Case 2. .
Let χ be a non-principle irreducible character of G and θ an irreducible constituent of . In this case, we have that or . If , then χ vanishes on , which implies that G has at most irreducible characters induced from irreducible characters of .
Since the non-principle linear irreducible characters of are not extendible to G, one has that , where . One the other hand, since p is the minimal prime divisor of , we get that . Let β be a non-principle irreducible character of and φ an irreducible character of such that . Then or .
Subcase 2.1. If is an abelian group, then G is isomorphic to the group listed in (iii).
Since is abelian, it follows by Lemma 2.1 that G is a Frobenius group with a kernel and a cyclic complement L of order p, where is a cyclic group of order and , as desired.
Subcase 2.2. If is not abelian, then there is no such group. In order to prove this, we write the proof into two subsubcases.
Subsubcase 2.2.1. Suppose there exists an irreducible character such that δ is extendible to G.
We first prove that is reducible and δ is the unique character of which is extendible to G. Let such that . Suppose is irreducible, then . Let be the set of all extensions of φ. If one of the elements in , say λδ, is extendible to G, then G has 2p non-linear irreducible characters lying over δ and λδ, and the 2p non-linear irreducible characters vanish at the elements where φ vanishes, contrary to G is a group. Therefore, all the elements of are not extendible to G. It is easy to check that for each , where . So vanishes at the elements where φ vanishes. Hence, G has exactly p irreducible characters lying over δ and k irreducible characters lying over other characters in L, and the irreducible characters vanish on the elements where φ vanishes, contrary to . Thus is reducible. If is extendible to G, by the same arguments as above, one has that γ is reducible, which implies that both δ and γ vanish at . Moreover, G has 2p non-linear irreducible characters lying over δ and γ, and the 2p characters vanish on the elements of , which leads to a contradiction since G is a group. Hence, δ is the unique character of which is extendible to G.
Let such that η is reducible. If for some , then . Since , we have that , which implies that is reducible for any . On the other hand, if is irreducible, by the same reason as above, one has that is irreducible for any . It is easy to check that if two of the characters are extensions of μ for some and , then all the characters are extensions of μ. Hence, we can get that or . If , then is abelian and which is an even number, a contradiction. So . Let and where . If and , then , which is an even number, a contradiction. Also, if and , then , a contradiction. Hence, , so is abelian and (co-prime to ), , , , and so . Therefore, G has a normal -complement H. Moreover, we have that and , and so is abelian, a contradiction.
Subsubcase 2.2.2. Suppose all the non-linear irreducible characters of are not extendible to G.
By Lemma 2.3, G is a Frobenius group with a kernel and a cyclic complement L of order p. Furthermore, we have that G has at most non-linear irreducible characters. It follows by Lemma 2.6 that is an elementary q-group and , where . But G is a non-solvable group, an obvious contradiction.
Conversely, it is easy to check that all these groups listed in Theorem B are obvious -groups. This completes the proof of Theorem B. □
References
Moretó A, Sangroniz J: On the number of zeros in the columns of the character table of a group. J. Algebra 2004, 279: 726–736. 10.1016/j.jalgebra.2004.01.016
Chillag D: On zeros of characters of finite groups. Proc. Am. Math. Soc. 1999, 127: 977–983. 10.1090/S0002-9939-99-04790-5
Gagola SM: Characters vanishing on all but two conjugacy classes. Pac. J. Math. 1983, 109: 363–385.
Isaacs IM: Character Theory of Finite Groups. Academic Press, New York; 1976.
Isaacs IM, Navarro G: Finite group elements where no irreducible character vanishes. J. Algebra 1999, 222: 413–423. 10.1006/jabr.1999.8007
Qian G: Finite groups in which each irreducible character has at most two zeros. Adv. Math. (China) 2002, 32(1):77–78.
Qian G: Bounding the fitting height of a solvable group by the number of zeros in a character table. Proc. Am. Math. Soc. 2002, 130: 3171–3176. 10.1090/S0002-9939-02-06452-3
Qian, G: Arithmetical conditions of characters and the structures of finite group. PhD thesis, Wuhan University (2002)
Qian G: Multiplicity of character degrees and the structure of solvable groups. Acta Math. Sin. 2004, 47(1):125–130.
Seitz G: Finite groups having only one irreducible representation of degree greater than one. Proc. Am. Math. Soc. 1968, 19: 459–461. 10.1090/S0002-9939-1968-0222160-X
Wolf TR: Character correspondences in solvable groups. Ill. J. Math. 1978, 22: 327–340.
Xu HJ, Zhang GX: The distribution of zeros in the character tables and the structure of finite groups. J. Southwest China Norm. Univ. 2006, 31(2):13–15. in Chinese
Xu HJ, Zhang GX, Chen GY: Finite groups of odd order which have at most p zeros in every column of the character table. Chin. Ann. Math., Ser. A 2009, 30: 291–296.
Yang CF: A characterization of Frobenius groups with characters. J. Southwest China Norm. Univ. 2001, 26(2):129–131.
Zhang GX: The finite groups who have only two non-linear irreducible character degrees. Chin. Ann. Math., Ser. A 1996, 17(2):227–232.
Zhu LR, Zeng JW: The finite groups with the same degree and the prime number of non-linear irreducible characters. Adv. Math. 2008, 38(2):199–203.
Zhmud EM: On finite groups having an irreducible complex character with one class of zeros. Sov. Math. Dokl. 1979, 20: 795–797.
Acknowledgements
Supported by Natural Science Foundation of China (Grant No.11171364); by ‘the Fundamental Research Funds for the Central Universities’ (Grant No. XDJK2012D004; XDJK2009C074) and Natural Science Foundation Project of CQ CSTC (Grant No. cstc2011jjA00020; cstc2012jjA0038); by Graduate-Innovation Funds of Science of SWU (ky2009013).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
YY carried out the study of the zeros in the character table of group of odd order. HX and GC carried out the study of the zeros in the character table of group of even order. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yan, Y., Xu, H. & Chen, G. On finite groups with their character tables having at most zeros in each column. J Inequal Appl 2012, 152 (2012). https://doi.org/10.1186/1029-242X-2012-152
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-152
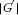 , is a prime number;
, is a prime number;