- Research
- Open access
- Published:
Existence and uniqueness of maximizers of a class of functionals under constraints: optimal conditions
Journal of Inequalities and Applications volume 2012, Article number: 151 (2012)
Abstract
In this article, we establish optimal assumptions under which general Hardy-Littlewood and Riesz-type functionals are maximized by balls. We also determine additional hypotheses such that balls are the unique maximizers. In both cases, we prove that our assumptions are optimal.
1 Introduction
Functional optimization under constraints plays a crucial role in many important areas like economics [1], physics, and engineering [3]. In many relevant cases, one needs very precise informations about maximizers or minimizers, especially in economics where the integrand represents the cost function, see [1] and references therein for a more detailed account. In this article, we will discuss such a case and a variational problem for steady axisymmetric vortex-rings in which kinetic energy is maximized subject to a prescribed impulse involving Riesz-type functionals under constraints [2, 3]. Burton [2] proved the existence of maximizers in a natural constraint set, and then showed that optimizers are unique (up to translations). In [3], we have extended his result to general Riesz-type functionals, which enabled us to treat a much larger class of functionals.
In this article, we develop an innovative approach based on a powerful result in mass transportation theory [4], Theorem 1], which turns out to be very fruitful for our purpose. We are convinced that our method applies to other optimization problems. This approach is also very efficient to give some estimates [5]. First, we have established suitable conditions to prove that balls are maximizers of the Hardy-Littlewood-type functionals (Part 1, Theorem 1). Note that this result improves [6], Proposition 3.1], in which Draghici and Hajaiej [7] needed the superfluous supermodularity of the integrand. It also improves a result of [7] in which the author used a mass transportation technique. We have then focused our attention to prove the optimality of our hypotheses. We also prove the optimality of these results. Characterization and uniqueness of optimizers of Riesz-type functionals were established in [3], our new approach also allows us to weaken (Ψ3) of [3]; thanks to a subtle reduction of the Riesz-type functionals to the Hardy-Littlewood ones (Theorem 2). This reduction is always possible; we will then give detailed proofs for Hardy-Littlewood functionals, and results concerning Riesz-type functionals are immediate consequences.
2 Notations and preliminaries
-
For , μ is Lebesgue measure in .
-
For a Lebesgue measurable set A in , denotes its measure.
-
is the ball centered in the origin with radius 1.
-
For , .
-
is the set of measurable functions in .
From now on: is a Borel measurable function,
-
For :
(1)
is the Hardy-Littlewood type functional and
is the Riesz type functional.
-
For :
-
is the ball centered in the origin such that .
-
is the ball centered in the origin such that .
-
.
-
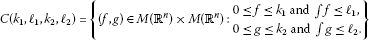 .
. -
A function is Schwarz-symmetric if it is radial and radially decreasing. We say that it is strictly Schwarz-symmetric if it is radial and strictly radially decreasing.
In this article, we are interested in the following maximization problems:
For u Schwarz symmetric, ;
and
3 Main results
In Theorem 1, we will suppose without loss of generality that for .
Theorem 1 Part 1 (Balls are maximizers of the Hardy-Littlewood type functionals)
The following assertions are equivalent:
H1 For any, u Schwarz symmetric, (I1) admits the functionas a maximizer.
H2 The function F satisfies the monotonicity properties:


Part 2 (Balls are the unique maximizers of the Hardy-Littlewood type functionals) (A) = For every, u Schwarz symmetric, if (I1) admitsas a unique maximizer, then; (B) = , . , ..Conversely, if(B′) = , . , . u is strictly Schwarz symmetric, then; (A′) = for any, u, is the unique maximizer of (I1)..
4 Proof
Part 1:
First note that is well-defined for any [6], Proposition 3.1]. Let us prove that (H2) implies (H1). Let , since , we have that .
Hence . Thus it suffices to prove the inequality:
Decomposing the left-hand side of the above inequality into integrals over and , we can rewrite it as:
But , and .
Therefore, it remains to verify that:
which holds true since .
Let us now prove that (H1) implies (H2).
:
Let us assume that for any and , we want to prove (3) and (4).
Let with fixed. Since , we can chose such that . Let us set , , , . Choose such that .
Therefore .
But
implying that
and (3) follows immediately.
Now we would like to prove (4).
For any and fixed, define , . Select such that . Therefore, . Set , and by our assumption .
But:
from which we deduce that
We now turn to the proof of Part 2 of our result: .
We are assuming that for every Schwarz symmetric function u and , . Then (8) and (6) hold true with strict sign, it follows that (3) and (4) are strict.
:
Here all inequalities in the proof of Part 1, become strict inequalities which permit us to conclude.
Remark 1 Note that cannot be done if u is strictly Schwarz symmetric since in our construction, we need u to be constant on some domains. However for any u Schwarz symmetric function the condition for with is necessary for the uniqueness of the maximizer. More precisely consider . For any where , f is a maximizer of (I1) independently of the choice of u since .
Theorem 2 Part 1 (Balls are maximizers of the Riesz-type functionals)
Suppose thatsatisfies:
(F1)
-
(i)
, ,
-
(ii)
, ,
(F2) , .
(j1) is non-increasing, then for any:
Part 2 Uniqueness of the maximizers (up to translations)
If in addition (F 1), (F 2), and (j 1) hold true with strict sign then for any
whereandare translates by the same vector ofand (respectively).
Proof First note that (F2) together with the fact that imply that F is non-decreasing with respect to each variable, and consequently it is non-negative. Let . (F2) together with (j1) imply that: ( denotes the Schwarz symmetrization of f) by [8], Theorem 1]. Thanks to (F1)(i):
where .
By Theorem 1,

Similarly, using (F1)(ii), we deduce that .
In conclusion, for any , we obtain
Using equality cases established in [8], Theorem 1] and Part 2 of Theorem 1, we can easily prove Part 2 of Theorem 2. □
References
Brenier Y: Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Math. 1991, 44(4):375–471. 10.1002/cpa.3160440402
Carlier G: On a class of multidimensional optimal transportation problems. J. Convex Anal. 2003, 10(2):517–529.
Burton GR: Vortex-rings of prescribed impulse. Math. Proc. Camb. Philos. Soc. 2003, 134(3):515–528. 10.1017/S0305004102006631
Hajaiej H: Balls are maximizers of the Riesz-type functionals with supermodular integrands. Ann. Mat. Pura Appl. 2010, 189: 395–401. 10.1007/s10231-009-0114-9
Hjaiej, H: The quantitative deficit in the Hardy-Littlewood inequality under constraint. J. Nonlinear Convex Anal. (in press)
Draghici C, Hajaiej H: Uniqueness and characterization of maximizers of integral functionals with constraints. Adv. Nonlinear Stud. 2009, 9: 215–226.
Hajaiej, H: Characterization of maximizers under constraints via mass transportation techniques. Preprint
Burchard A, Hajaiej H: Rearrangement inequalities for functionals with monotone integrands. J. Funct. Anal. 2006, 233(2):561–582. 10.1016/j.jfa.2005.08.010
Acknowledgements
The author extend his appreciation to the Deanship of Scientific Research at King Saud University for funding the work through the research group project No RGP-VPP-124.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hajaiej, H. Existence and uniqueness of maximizers of a class of functionals under constraints: optimal conditions. J Inequal Appl 2012, 151 (2012). https://doi.org/10.1186/1029-242X-2012-151
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-151
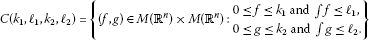 .
.