- Research
- Open Access
- Published:
A note on the Königs domain of compact composition operators on the Bloch space
Journal of Inequalities and Applications volume 2011, Article number: 31 (2011)
Abstract
Let 
be the unit disk in the complex plane. We define 
to be the little Bloch space of functions f analytic in which satisfy lim|z|→1(1 - |z|2)|f'(z)| = 0. If 
is analytic then the composition operator C
φ
: f ↦ f ∘ φ is a continuous operator that maps into itself. In this paper, we show that the compactness of C
φ
, as an operator on , can be modelled geometrically by its principal eigenfunction. In particular, under certain necessary conditions, we relate the compactness of C
φ
to the geometry of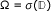 
, where σ satisfies Schöder's functional equation σ ∘ φ = φ'(0)σ.
2000 Mathematics Subject Classification: Primary 30D05; 47B33 Secondary 30D45.
1 Introduction
Let 
be the unit disk in the complex plane and 
its boundary. We define the Bloch space 
to be the Banach space of functions, f, analytic in with
This space has many important applications in complex function theory, see [1] for an overview of many of them. We denote by the little Bloch space of functions in that satisfy lim|z|→1(1 - |z|2)|f '(z)| = 0. This space coincides with the closure of the polynomials in .
Suppose now that is analytic, then we may define the operator, C
φ
, acting on as f ↦ f ∘ φ. It was shown in [2] that every such operator maps continuously into itself. Moreover, it was proved that C
φ
is compact on if and only if φ satisfies
Recall that the hyperbolic geometry on is defined by the distance
where the infimum is taken over all sufficiently smooth arcs that have endpoints z and w.
Here, 
is the Poincaré density of . The hyperbolic derivative of φ is given by φ'(z)/(1 - |φ(z)|2) and functions that satisfy (1) are called little hyperbolic Bloch functions or written 
.
The Schröder functional equation is the equation
Note that this is just the eigenfunction equation for C φ . Kœnigs' theorem states that if φ has fixed point at the origin then (2) has a unique solution for γ = φ'(0) which we call the Kœnigs function and denote by σ from here on. In the study of the geometric properties of φ in relation to the operator theoretic properties of C φ , it has become evident that the Kœnigs function is much more fruitful to study than φ itself. In particular, see [3] for a discussion of the Kœnigs function in relation to compact composition operators on the Hardy spaces.
If we let 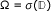be the Kœnigs domain of φ, then (2) may be interpreted as implying that the action of φ on is equivalent to multiplication by γ on Ω. It is due to this that the pair (Ω, γ ) is often called the geometric model for φ.
In this paper, we study the geometry of Ω when . In order to do this, we will use the hyperbolic geometry of Ω. If 
is a universal covering map and Ω is a hyperbolic domain in ℂ, then the Poincaré density on Ω is derived from the equation
which is independent of the choice of f. Since this equation, in terms of differentials, is 
(for w = f (z)), we see that the hyperbolic distance on defined above carries over to a hyperbolic distance on Ω. For a more thorough treatment of the hyperbolic metric, see [4].
In [5], the Königs domain of a compact composition operator on the Hardy space was studied and the following result was proved.
Theorem A. Let φ be a univalent self-map ofwith a fixed point in. Suppose that for some positive integer n0there are at most finitely many points ofat which
has an angular derivative. Then the following are equivalent.
-
1.
Some power of C φ is compact on the Hardy space H2;
-
2.
σ lies in Hp for every p < ∞;
-
3.
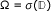does not contain a twisted sector.
Here, Ω is said to contain a twisted sector if there is an unbounded curve Γ ∈ Ω with
for some ε > 0 and all w ∈ Γ, where δΩ is the distance from w to the boundary of Ω as defined below. The purpose of this paper is to provide a similar result to this in the context of the Bloch space.
2 Simply connected domains
Throughout this section, we assume that Ω is an unbounded simply connected domain in ℂ with 0 ∈ Ω. As in the previous section, σ represents the Riemann mapping of onto Ω with σ(0) = 0 and σ'(0) > 0. We will also define φ via the Schröder functional equation. Throughout we let
so that δΩ(w) is the Euclidean distance from w to the boundary of Ω.
Theorem 1. Let φ be a univalent function mappinginto, φ(0) = 0. Suppose that the closure of
intersectsonly at finitely many fixed points and is contained in a Stolz angle of opening no greater than απ there.
If |φ'(0)| > 16 tan(απ/ 2) then the following are equivalent
1. C
φ
is compact on;
2. 
;
3. For every n > 0, 
.
Remark: It has recently been shown by Smith [6] that compactness of C
φ
on is equivalent to compactness of C
φ
on , BMOA and VMOA when φ is univalent and so in the above theorem, the first condition could read: C
φ
is compact on , , BMOA and VMOA Before proceeding, we prove the following lemma.
Lemma 1. Under the hypotheses of the theorem, w and γw tend to the same prime end at ∞, and ∂γ Ω ⊂ Ω.
Proof. The first assertion follows from the fact that the closure of touches only at fixed points. Suppose now that the second assertion is false and there are distinct prime ends ρ1 and ρ2 with ρ1 = γρ2. Then under the boundary correspondence given by σ there are distinct points η, 
with
It follows that 
and therefore ζ is a fixed point of φ. Hence, we have the contradiction ρ1 = ρ2. □
Proof. We first prove that 1 is equivalent to 2.
By the results of Madigan and Matheson [2], and Smith [6] cited above C
φ
is compact on if and only if
However, by Schröder's equation
Since Ω is simply connected, λΩ (w) ≍ 1/δΩ (w) and so C
φ
is compact on if and only if
Since γ Ω ⊂ Ω, γw → ∂Ω implies that w → ∂Ω. Therefore, (3) holds if and only if
By the Lemma, we see that γw → ∂Ω means w → ∞ and w ∈ γ Ω, and we have shown that 1 and 2 are equivalent.
Suppose that 2 holds and let ε > 0 be given. Then we can find a R > 0 so that δΩ (w) <εδΩ (γw) for all |w| > R, since there are only a finite number of prime ends at ∞. Choose w ∈ Ω arbitrarily with modulus greater than R and let n satisfy |γ|-nR < |w| ≤ |γ |-n -1R.
Then we have that δΩ (w) < εnδΩ (γn w) and hence
Now as w → ∞ in γ Ω, γnw lies in a closed set properly contained in Ω and therefore δΩ (γn w) is bounded below by a constant independent of w. We thus have that
and since ε was arbitrary, the left-hand side of the above inequality must tend to ∞. Hence, we have shown that limw→∞|w| β δΩ (w) = 0 for every β > 0.
Now may be interpreted geometrically as limw→∂Ωn|w| n-1δΩ (w) = 0 and this follows from the above argument. Therefore, 2 implies 3.
To show that 3 implies 2, we need to show that if
then 2 holds.
To complete the proof, we require the following lemma whose proof we merely sketch.
Lemma 2. Under the hypotheses of the theorem,
Sketch of Proof. First note that
Now if lies in a non-tangential angle of opening απ at ζ, then a short calculation shows that
and the assertion follows. □
Now with f defined above, we have
for large enough w. Hence,
as w → ∞ and so 2 holds. □
It is of interest to consider the growth of σ since condition 3 would imply that it has very slow growth. The following corollary follows from 3 and the fact that functions in grow at most of order log 1/(1 - |z|).
Corollary 1. Suppose that φ satisfies the hypotheses of the Theorem and that any of the equivalent conditions holds, then for r = |z|.
We also provide the following restatement of the hypotheses of Theorem 1 to illustrate the main properties of the Königs domain.
Corollary 2. Let Ω be an unbounded domain in ℂ with γ Ω ⊂ Ω and 0 ∈ Ω. Suppose that has Ω only finitely many prime ends at ∞ and
In addition, suppose that ∂γ Ω ⊂ Ω. If
, σ(0) = 0, σ'(0) > 0, and φ is defined by Schröder's equation, then the following are equivalent.
1. C
φ
is compact on;
2. ;
3. For every n > 0, .
The hypothesis on the boundary of Ω is vital. If we do not assume that ∂γ Ω ⊂ Ω, then we deduce from the proof of the Theorem that is equivalent to
In this situation, the finite part of the boundary of Ω plays a complicated role in the behaviour of φ. We conclude this section by constructing a domain that displays very bad boundary properties. This answers a question of Madigan and Matheson in [2].
In [2] it was shown that if ∂φ(D) touches 
in a cusp, then . However, it is not sufficient that ∂φ(D) touches at an angle greater that 0. The question was raised of whether or not it is possible that 
can be infinite.
With the hypothesis that ∂γ Ω ⊂ Ω the prime ends at ∞ correspond to points of 
that touch . Therefore, 
is at most countable. A natural question to ask is whether or not 
can ever be positive, where Λ represents linear measure.
This example is well known in the setting of the unit disk, see [7, Corollary 5.3]. We describe here the construction in terms of the Königs domain.
Theorem 2. There is a univalent functionsuch that
.
Proof. We construct the domain Ω so that it satisfies (4). Let 0 < γ < 1 be given. We will define a nested sequence 
, n = 1, 2, ... so that
where Θ n ⊂ Θn+1for all n = 1, 2, ....
First let N > 2 be chosen arbitrarily and let Θ1 = {2πk/N : k = 0, ..., N - 1}.
Suppose now that Θ n has been defined, then let Θn+1be such that Θ n ⊂ Θn+1and whenever θ ∈ Θ n is isolated, we define a sequence θ k ∈ Θn+1, k = 1, 2, ..., so that θ k → θ as k → ∞ and for each k there is a j so that θ - θ k = θ j -θ . Moreover, assume that
In this way, we define the sequence of sets Θ
n
, n = 1, 2, .... We will, furthermore, assume that for each 
, there is a sequence θ
n
∈ Θ
n
, n = 1, 2, ...., such that θ
n
→ θ.
We claim that this gives the desired domain Ω with boundary defined by (5).
To see this, let γw ∈ Ω be arbitrary, then by construction, we may find a ζ ∈ ∂Ω so that δΩ (γw) = |ζ - γw|. It is readily seen that for such ζ, there is an n so that ζ ∈ {reiθ: r ≥ γ-n} for some θ ∈ Θ n and moreover, θ is isolated in Θ n .
If we now consider w, we may find a sequence θ
k
→ θ as k → ∞ so that 
for all k hence we may fix a k so that δΩ (w) = |w - n| for 
.
By estimating the line segment [w, η] by the arc of 
joining w to η, we see that δΩ (w) ≍ |w|| α - θ
k
| where w = reiα.Therefore, we have the estimate δΩ (w) ≤ |w||θk+1- θ
k
|. By a similar argument, we deduce the estimate δΩ (γw) ≍ |γw||θ - θ
k
| and so
by (6) and so the construction is complete.
We claim that if is defined as usual and φ is given by Schröder's equation, then 
.
In fact, if θ ∈ Θ
n
is isolated, then the ray R = {reiθ: r ≥ γ-n-1} is contained in a single prime end of Ω. Therefore, to each such ray, there exists a point that corresponds to R under σ. Since γR ⊂ ∂Ω, we thus have that ζ corresponds to a prime end p under φ with 
.
On the other hand, if θ ∈ Θ
n
is isolated, then R' = {reiθ: γ-n≤ r < γ-n-1} satisfies γR'∩ ∂Ω = ∅, and so there is an arc 
such that σ (ρ
θ
) = R' and ρ
θ
has an end-point in .
Hence, each 
is contained in a prime end of and
The result follows. □
3 Multiply connected domains
The geometric arguments of the previous section potentially lend themselves to multiply connected domains in the following way. Suppose that Ω is a domain in ℂ with 0 ∈ Ω and γ Ω ⊂ Ω for some 
. Let σ be a universal covering map of onto Ω with σ(0) = 0. Then σ'(0) ≠ 0 and we may define φ via (2). Now we have
However, if Ω is not simply connected, then σ is an infinitely sheeted covering of Ω and therefore the equation σ (z) = 0 has infinitely many distinct solutions, z n , n = 0, 1, ....
Now, since
for all n ≥ 0, we see that 
. Thus, we have proved the following result.
Proposition 1. Suppose that Ω ⊂ ℂ is a domain satisfying 0 ∈ Ω and γ Ω ⊂ Ω, and letbe a universal covering map with σ(0) = 0.
If φ, as defined by (2) is in
then Ω is simply connected.
References
- 1.
Anderson JM: Bloch Functions: The Basic Theory. Operators and Function Theory. D Reidel 1985, 1–17.
- 2.
Madigan K, Matheson A: Compact Composition Operators on the Bloch Space. Trans Am Math Soc 1995, 347: 2679–2687. 10.2307/2154848
- 3.
Shapiro JH: Composition Operators and Classical Function Theory. Springer 1993.
- 4.
Ahlfors LV: Conformal Invariants, Topics in Geometric Function Theory. McGraw-Hill 1973.
- 5.
JH Shapiro, W Smith, A Stegenga: Geometric models and compactness of composition operators. J Funct Anal 1995, 127: 21–62. 10.1006/jfan.1995.1002
- 6.
Smith W: Compactness of composition operators on BMOA. Proc Am Math Soc 1999, 127: 2715–2725. 10.1090/S0002-9939-99-04856-X
- 7.
Bourdon P, Cima J, Matheson A: Compact composition operators on BMOA. Trans Am Math Soc 1999, 351: 2183–2196. 10.1090/S0002-9947-99-02387-9
Author information
Affiliations
Corresponding author
Additional information
4 Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jones, M.M. A note on the Königs domain of compact composition operators on the Bloch space. J Inequal Appl 2011, 31 (2011). https://doi.org/10.1186/1029-242X-2011-31
Received:
Accepted:
Published:
Keywords
- Unit Disk
- Hardy Space
- Composition Operator
- Connected Domain
- Hyperbolic Geometry
