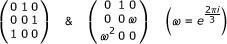Generalized ulam-hyers stability of C*-Ternary algebra n-Homomorphisms for a functional equation

Abstract

In this article, we investigate the Ulam-Hyers stability of C*-ternary algebra n-homomorphisms for the functional equation:

in C*-ternary algebras.

2000 Mathematics Subject Classification: Primary 39B82; 46B03; 47Jxx.

1. Introduction and preliminaries

Ternary algebraic operations were considered in the nineteenth century by several mathematicians, such as Cayley [1] who introduced the notion of cubic matrix, which, in turn, was generalized by Kapranov et al. [2]. The simplest example of such nontrivial ternary operation is given by the following composition rule:

Ternary structures and their generalization, the so-called n-array structures, raise certain hopes in view of their applications in physics. Some significant physical applications are as follows (see [3]):

• (1) The algebra of nonions generated by two matrices

  

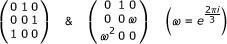
was introduced by Sylvester as a ternary analog of Hamilton's quaternions [4].

• (2) The quark model inspired a particular brand of ternary algebraic systems. The so-called Nambu mechnics is based on such structures [5].

There are also some applications, although still hypothetical, in the fractional quantum Hall effect, the non-standard statistics, supersymmetric theory, and Yang-Baxter equation [4, 6].

A C*-ternary algebra is a complex Banach space A, equipped with a ternary product (x, y, z) α [x, y, z] of A³ into A, which is ℂ-linear in the outer variables, conjugate ℂ-linear in the middle variable, and associative in the sense that [x, y, [z, w, v]] = [x, [w, z, y], v] = [[x, y, z], w, v], and satisfies ||[x, y, z]|| ≤ ||x|| · ||y|| · ||z|| and ||[x, x, x]|| = ||x||³ (see [7, 8]). Every left Hilbert C*-module is a C*-ternary algebra via the ternary product [x, y, z] := 〈x, y〉 z.

If a C*-ternary algebra (A,[·, ·, ·]) has an identity, i.e., an element e ∈ A such that x = [x, e, e] = [e, e, x] for all x ∈ A, then it is customary to verify that A, endowed with x ∘ y := [x, e, y] and x* := [e, x, e], is a unital C*-algebra. Conversely, if (A, ∘) is a unital C*-algebra, then [x, y, z] := x ∘ y* ∘ z makes A into a C*-ternary algebra.

Let A and B be C*-ternary algebras. A ℂ-linear mapping H : A → B is called a C*-ternary algebra homomorphism if

for all x, y, z ∈ A.

Definition. Let A and B be C*-ternary algebras. A multilinear mapping H : Aⁿ → B over ℂ is called a C*-ternary algebra n-homomorphism if it satisfies

for all x₁, y₁, z₁, · · ·, x _n , y _n , z _n ∈ A.

In 1940, Ulam [9] gave a talk before the Mathematics Club of the University of Wisconsin in which he discussed a number of unsolved problems. Among these was the following question concerning the stability of homomorphisms:

We are given a group G and a metric group G' with metric ρ(·, ·). Given ε > 0, does there exist a δ > 0 such that if f : G → G' satisffies ρ(f(xy), f(x) f(y)) < δ for all x, y ∈ G, then a homomorphism h : G → G' exists with ρ(f(x), h(x)) < ε for all x ∈ G ?

In 1941, Hyers [10] gave the first partial solution to Ulam's question for the case of approximate additive mappings under the assumption that G₁ and G₂ are Banach spaces. Then, Aoki [11] and Bourgin [12] considered the stability problem with unbounded Cauchy differences. In 1978, Rassias [13] generalized the theorem of Hyers [10] by considering the stability problem with unbounded Cauchy differences. In 1991, Gajda [14], following the same approach as that by Rassias [13], gave an affirmative solution to this question for p > 1. It was shown by Gajda [14] as well as by Rassias and Šemrl [15], that one cannot prove a Rassias-type theorem when p = 1. Găvruta [16] obtained the generalized result of Rassias's theorem which allows the Cauchy difference to be controlled by a general unbounded function. During the last two decades, a number of articles and research monographs have been published on various generalizations and applications of the generalized Hyers-Ulam stability to a number of functional equations and mappings, for example, Cauchy-Jensen mappings, k-additive mappings, invariant means, multiplicative mappings, bounded n th differences, convex functions, generalized orthogonality mappings, Euler-Lagrange functional equations, differential equations, and Navier-Stokes equations. The instability of characteristic flows of solutions of partial differential equations is related to the Ulam's stability of functional equations [17]-[24]. On the other hand, the authors [25], Park [20] and Kim [26] have contributed studies in respect of the stability problem of ternary homomorphisms and ternary derivations.

2. Solution and stability

Let X and Y be real or complex vector spaces and n ≥ 2 an integer. For a mapping f : Xⁿ → Y, consider the functional equation:

(2.1)

The above functional equation is rewritten as

(2.2)

where

We solve the general problem in vector spaces for the n-additive mappings satisfying (2.1).

Theorem 2.1. A mapping f : Xⁿ → Y satisffies the equation (2.1) if and only if the mapping f is n-additive.

Proof. Assume that f satisfies (2.1). Letting x₁ = y₁ = · · · = x _n = y _n = 0 in (2.2), we get f(0, · · ·, 0) = 0. Letting y₁ = x₂ = y₂ = · · · = x _n = y _n = 0 in (2.2), we have

for all x₁ ∈ X. Similarly, we get

for all x₂, · · ·, x _n ∈ X. Setting y₁ = y₂ = 0 and x₃ = y₃ = · · · = x _n = y _n = 0 in (2.2), we have

for all x₁, x₂ ∈ X. Similarly, we get f(x₁, 0, x₃, 0, · · ·, 0) = · · · = f(0, · · ·, 0, x_n-1, x _n ) = 0 for all x₁, · · ·, x _n ∈ X.

Continuing this process, we obtain that f(x₁, · · ·, x _n ) = 0 for all x₁, · · ·, x _n ∈ X with x _i = 0 for some i = 1, · · ·, n. Letting y₂ = · · · = y _n = 0 in (2.2), we get the additivity in the first variable. Similarly, the additivities in the remaining variables hold.

The converse is obvious. □

We investigate the generalized Ulam's stability in C*-ternary algebras for the n-additive mappings satisfying (2.1).

Lemma 2.2. Let X and Y be complex vector spaces and let f : Xⁿ → Y be a n-additive mapping such that

for alland all x₁, · · ·, x _n ∈ X, then f is n-linear over ℂ.

Proof. Since f is n-additive, we get for all x₁, · · ·, x _n ∈ X. Now let and M be an integer greater than 2(|σ₁| + · · · + |σ _n |). Since , there is such that . Now

for some . Thus, we have

for all x₁, · · ·, x _n ∈ X. Hence, the mapping f : Xⁿ → Y is n-linear over ℂ. □

Using the above lemma, one can obtain the following result.

Theorem 2.3. Let X and Y be complex vector spaces and let f : Xⁿ → Y be a mapping such that

(2.3)

for alland all x_1,1, x_2,1, · · ·, x_1,n, x_2,n∈ X. Then, f is n-linear over ℂ.

Proof. Letting λ₁ = · · · = λ _n = 1, by Theorem 1.1, f is n-additive. Letting x_2,1 = · · · = x_2,n= 0 in (2.3), we get f(λ₁x₁, · · ·, λ _n x _n ) = λ₁ · · · λ _n f(x₁, · · ·, x _n ) for all and all x₁, · · ·, x _n ∈ X. Hence, by Lemma 2.2, the mapping f is n-linear over ℂ. □

From now on, assume that A is a C*-ternary algebra with norm || · || _A and that B is a C*-ternary algebra with norm || · || _B .

For a given mapping f : Aⁿ → B, we define

for all and all x_1,1, x_2,1, · · ·, x_1,n, x_2,n∈ A.

We prove the generalized Ulam-Hyers stability of homomorphisms in C*-ternary algebras for the functional equation

Theorem 2.4. Let p₁, ···, p _n ∈ (0, ∞) withand θ ∈ (0, ∞), and let f : Aⁿ → B be a mapping such that

(2.4)

and

(2.5)

for alland all x₁, y₁, z₁, · · ·, x _n , y _n , z _n ∈ A. Then, there exists a unique C*-ternary algebra n-homomorphism H : Aⁿ → B such that

(2.6)

for all x₁, · · ·, x _n ∈ A.

Proof. Letting λ₁ = · · · = λ _n = 1, y₁ = x₁, · · ·, y _n = x _n in (2.4), we gain

(2.7)

for all x₁, · · ·, x _n ∈ A. Thus, we have

for all x₁, · · ·, x _n ∈ A and all j ∈ ℕ. For given integer l, m(0 ≤ l < m), we obtain that

(2.8)

for all x₁, · · ·, x _n ∈ A. Since , the sequence

is a Cauchy sequence for all x₁, ···, x _n ∈ A. Since B is complete, the sequence converges for all x₁, · · ·, x _n ∈ A. Define H : Aⁿ → B by

for all x₁, · · ·, x _n ∈ A. Letting l = 0 and taking m → ∞ in (2.8), one can obtain the inequality (2.6). By (2.4), we see that

for all x₁, y₁, · · ·, x _n , y _n ∈ A and all s. Since , letting s → ∞ in the above inequality, H satisfies (2.1). By Theorem 2.1, H is n-additive.

Letting y₁ = x₁, · · ·, y _n = x _n in (2.4), we gain

for all and all x₁, · · ·, x _n ∈ A. Thus we have

for all , all x₁, · · ·, x _n ∈ A and all m ∈ ℕ. Hence, we get

for all x₁, · · ·, x _n ∈ A and all m ∈ ℕ, and one can show that

for all , all x₁, · · ·, x _n ∈ A and all m ∈ ℕ. Hence,

for all , all x₁, · · ·, x _n ∈ A and all m ∈ ℕ. Since , we have

as m → ∞ for all and all x₁, · · ·, x _n ∈ A. Hence

for all and all x₁, ···, x _n ∈ A. From Lemma 2.2, the mapping H : Aⁿ → B is n-linear over ℂ. It follows from (2.5) that

for all x₁, y₁, z₁, ···, x _n , y _n , z _n ∈ A. So

for all x₁, y₁, z₁, ···, x _n , y _n , z _n ∈ A.

Now, let T : Aⁿ → B be another n-additive mapping satisfying (2.6). Then, we have

which tends to zero as m → ∞ for all x₁, ···, x _n ∈ A. Hence, we can conclude that H(x₁, ···, x _n ) = T(x₁, ···, x _n ) for all x₁, ···, x _n ∈ A. This proves the uniqueness of H.

Thus, the mapping H : A→B is a unique C*-ternary algebra n-homomorphism satisfying (2.6). □

Letting p₁ = ··· = p _n = 0 and θ = ε in Theorem 2.4, we obtain the Ulam-Hyers stability for the n-additive functional equation (2.1).

Corollary 2.5. Let ε ∈ (0, ∞) and let f : Aⁿ → B be a mapping satisfying

and

for alland all x₁, y₁, z₁ ···, x _n , y _n , z _n ∈ A. Then, there exists a unique C*-ternary algebra n-homomorphism H : Aⁿ → B such that

for all x₁, ···, x _n ∈ A.

Example 2.6. We present the following counterexample modiffied by the well-known counterexample of Z. Gajda[14]for the functional equation (2.1). Set θ > 0 and let.

Deffine a function f :ℝ ⁿ → ℝ by

for all x₁, ···, x _n ∈ ℝ, where ϕ _μ : ℝ ⁿ → ℝ is the function given by

for all x₁, ···, x _n ∈ ℝ. Deffine another function g : ℝ → ℝ by

for all x ∈ ℝ.

For all m ∈ ℕ and all, we assert that

(2.9)

It was proved in[14]that

for all x, y ∈ ℝ, that is, (2.9) holds for m = 1. For a ffixed k ∈ ℕ, assume that (2.9) holds for m = k. Then, we have

for all, that is, (2.9) holds for m = k + 1. Hence, (2.9) holds for all m ∈ ℝ.

Note that

(2.10)

for all x₁, ···, x _n ∈ ℝ. By the inequality (2.9) and the above equality, we see that

for all x₁, y₁, ···, x _n , y _n ∈ ℝ. However, we observe from[14]that

and so

Thus,

where h: ℝⁿ → ℝ is the function given by

for all x₁, ···, x _n ∈ ℝ. Hence, the function f is a counterexample for the singular caseof Theorem 2.4.

Theorem 2.7. Let p ∈ (0,n) and θ ∈ (0, ∞), and let f : Aⁿ → B be a mapping such that

(2.11)

and

(2.12)

for alland all x₁, y₁, z₁ ···, x _n , y _n , z _n ∈ A. Then, there exists a unique C*-ternary algebra n-homomorphism H : Aⁿ→B such that

for all x₁, ···, x _n ∈ A.

Proof. The proof is similar to the proof of Theorem 2.4. □

Example 2.8. We present the following counterexample modiffied by the well-known counterexample of Z. Gajda[14]for the functional equation (2.1). Set θ > 0 and let

Let f : ℝⁿ → ℝ and g : ℝ → ℝ be the same as in Example 2.6. By the same argument as in Example 2.6, for all m ∈ ℕ and all, one can obtain that g satisffies the inequality:

By the equality (2.10) and the above inequality, we see that

for all x₁, y₁, ···, x _n , y _n ∈ ℝ. For each x₁, y₁, ···, x _n , y _n ∈ ℝ, let M(x₁, y₁, ···, x _n , y _n ) := max{|x₁|, |y₁|, ···, |x _n |, |y _n |}. We have

for all x₁, y₁, ···, x _n , y _n ∈ ℝ. Thus we have

for all x₁, y₁, ···, x _n , y _n ∈ ℝ. By the same reason as for Example 2.6, the function f is a counterexample for the singular case p = n of Theorem 2.7.

Theorem 2.9. Let p₁, ···, p _n ∈ (0, ∞) with, s ∈ (0, n) and θ, η ∈ (0, ∞), and let f: Aⁿ → B be a mapping such that

(2.13)

and

(2.14)

for alland all x_1,1, x_2,1, x_3,1, ···, x_{1, n}, x_{2, n}, x_{3, n}∈ A. Then, there exists a unique C*-ternary algebra n-homomorphism H: Aⁿ→ B such that

for all x₁, ···, x _n ∈ A.

Proof. The proof is similar to the proof of Theorem 2.4. □

Theorem 2.10. Let p₁, ···, p _n ∈ (0, ∞) withand θ ∈ (0, ∞), and let f : Aⁿ → B be a mapping satisfying (2.4) (2.5). Then, there exists a unique C*-ternary algebra n-homomorphism H : Aⁿ → B such that

(2.15)

for all x₁, ···, x _n ∈ A.

Proof. It follows from (2.7) that

for all x₁, ···, x _n ∈ A. Hence,

(2.16)

for all nonnegative integers m and l with m > l and all x₁, ···, x _n ∈ A. It follows from (2.16) that the sequence is a Cauchy sequence for all x₁, ···, x _n ∈ A. Since B is complete, the sequence converges. Hence, one can define the mapping H : Aⁿ → B by for all x₁, ···, x _n ∈ A. Moreover, letting l = 0 and passing the limit m → ∞ in (2.16), we get (2.15).

The remainder of the proof is similar to the proof of Theorem 2.4. □

Theorem 2.11. Let p ∈ (3n, ∞) and θ ∈ (0, ∞), and let f: Aⁿ → B be a mapping satisfying (2.11) (2.7), and f(0, ···, 0) = 0. Then, there exists a unique C*-ternary algebra n-homomorphism H : Aⁿ → B such that

for all x₁, ···, x _n ∈ A.

Proof. The proof is similar to that of Theorem 2.10. □

Theorem 2.12. Let p₁, ···, p _n ∈ (0, ∞) with, s ∈ (n, ∞) and θ, η ∈ (0, ∞), and let f: Aⁿ → B be a mapping such that (2.13), (2.14), and f(0, ···, 0) = 0. Then, there exists a unique C*-ternary algebra n-homomorphism H: Aⁿ → B such that

for all x₁, ···, x _n ∈ A.

Proof. The proof is similar to that of Theorem 2.10.