- Research
- Open access
- Published:
Some nonlinear delay integral inequalities on time scales arising in the theory of dynamics equations
Journal of Inequalities and Applications volume 2011, Article number: 29 (2011)
Abstract
In this paper, some new nonlinear delay integral inequalities on time scales are established, which provide a handy tool in the research of boundedness of unknown functions in delay dynamic equations on time scales. The established results generalize some of the results in Lipovan [J. Math. Anal. Appl. 322, 349-358 (2006)], Pachpatte [J. Math. Anal. Appl. 251, 736-751 (2000)], Li [Comput. Math. Appl. 59, 1929-1936 (2010)], and Sun [J. Math. Anal. Appl. 301, 265-275 (2005)].
MSC 2010: 26E70; 26D15; 26D10.
1 Introduction
In the 1980s, Hilger initiated the concept of time scales [1], which is used as a theory capable to contain both difference and differential calculus in a consistent way. Since then, many authors have expounded on various aspects of the theory of dynamic equations on time scales. For example [2–10], and the references therein. In these investigations, integral inequalities on time scales have been paid much attention by many authors, and a lot of integral inequalities on time scales have been established (see [5–10] and the references therein), which are designed to unify continuous and discrete analysis, and play an important role in the research of boundedness, uniqueness, stability of solutions of dynamic equations on time scales. But to our knowledge, delay integral inequalities on time scales have been paid little attention so far in the literature. Recent results in this direction include the works of Li [11] and Ma [12].
Our aim in this paper is to establish some new nonlinear delay integral inequalities on time scales, which are generalizations of some known continuous inequalities and discrete inequalities in the literature. Also, we will present some applications for the established results, in which we will use the present inequalities to derive new bounds for unknown functions in certain delay dynamic equations on time scales.
At first, we will give some preliminaries on time scales and some universal symbols for further use. Throughout this paper, R denotes the set of real numbers and R+ = [0, ∞), while Z denotes the set of integers. For two given sets G, H, we denote the set of maps from G to H by (G, H).
A time scale is an arbitrary nonempty closed subset of the real numbers. In this paper, T denotes an arbitrary time scale. On T, we define the forward and backward jump operators σ ∈ (T, T), and ρ ∈ (T, T) such that σ(t) = inf{s ∈ T, s > t}, ρ(t) = sup{s ∈ T, s < t}.
Definition 1.1: A point t ∈ T is said to be left-dense if ρ(t) = t and t ≠ inf T, right-dense if σ(t) = t and t ≠ sup T, left-scattered if ρ(t) < t and right-scattered if σ(t) > t.
Definition 1.2: The set T κ is defined to be T if T does not have a left-scattered maximum, otherwise it is T without the left-scattered maximum.
Definition 1.3: A function f ∈ (T, R) is called rd-continuous if it is continuous at right-dense points and if the left-sided limits exist at left-dense points, while f is called regressive if 1 + μ(t)f(t) ≠ 0, where μ(t) = σ(t) - t. C
rd
denotes the set of rd-continuous functions, while  denotes the set of all regressive and rd-continuous functions, and
denotes the set of all regressive and rd-continuous functions, and  .
.
Definition 1.4: For some t ∈ T κ, and a function f ∈ (T, R), the delta derivative of f at t is denoted by fΔ(t) (provided it exists) with the property such that for every ε > 0, there exists a neighborhood  of t satisfying
of t satisfying

Remark 1.1: If T = R, then fΔ(t) becomes the usual derivative f'(t), while fΔ(t) = f(t + 1) - f(t) if T = Z, which represents the forward difference.
Definition 1.5: If FΔ(t) = f(t), t ∈ T κ, then F is called an antiderivative of f, and the Cauchy integral of f is defined by

The following two theorem include some important properties for delta derivative on time scales.
Theorem 1.1 [[13], Theorem 2.2]: If a, b, c ∈ T, α ∈ R, and f, g ∈ C rd , then
-
(i)

,
-
(ii)

,
-
(iii)
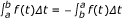
,
-
(iv)

,
-
(v)
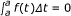
,
-
(vi)
if f(t) ≥ 0 for all a ≤ t ≤ b, then
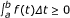 .
.
For more details about the calculus of time scales, we advise to refer to [14].
2 Main results
In the rest of this paper, for the sake of convenience, we denote T0 = [t0, ∞) ∩T, and always assume T0 ⊂ T κ.
Lemma 2.1 [15]: Assume that a ≥ 0, p ≥ q ≥ 0, and p ≠ 0, then for any K > 0

Lemma 2.2: Suppose u, a ∈ C
rd
,  , m ≥ 0, and a is nondecreasing. Then,
, m ≥ 0, and a is nondecreasing. Then,

implies

where e m (t, t0) is the unique solution of the following equation

Proof: From [[16], Theorem 5.6], we have  , t ∈ T0. Since a(t) is nondecreasing on T0, then
, t ∈ T0. Since a(t) is nondecreasing on T0, then  . On the other hand, from [[14], Theorem 2.39 and 2.36 (i)], we have
. On the other hand, from [[14], Theorem 2.39 and 2.36 (i)], we have  . Combining the above information, we can obtain the desired inequality.
. Combining the above information, we can obtain the desired inequality.
Theorem 2.1: Suppose u, a, b, f ∈ C rd (T0, R+), and a, b are nondecreasing. ω ∈ C(R+, R+) is nondecreasing. τ ∈ (T0, T), τ (t) ≤ t, -∞ < α = inf{τ(t), t ∈ T0} ≤ t0, ϕ ∈ C rd ([α, t0] ∩T, R+). p > 0 is a constant. If u(t) satisfies, the following integral inequality

with the initial condition

then

where G is an increasing bijective function, and

Proof: Let T ∈ T0 be fixed, and

Then considering a, b are nondecreasing, we have

Furthermore, for t ∈ [t0, T ] ∩T, if τ(t) ≥ t0, considering τ (t) ≤ t, then τ i (t) ∈ [t0, T ] ∩T, and from (6) we obtain

If τ(t) ≤ t0, from (2) we obtain

So from (7) and (8), we always have

Moreover,

that is,

On the other hand, for t ∈ [t0, T ] ∩T, if σ(t) > t, then

If σ(t) = t, then

where ξ lies between v(s) and v(t). So we always have  .
.
Using the statements above, we deduce that

Replacing t with s in the inequality above, and an integration with respect to s from t0 to t yields

where G is defined in (4).
Considering G is increasing, and v(t0) = a(T ), it follows that

Combining (6) and (12), we get

Taking t = T in (12), yields

Since T ∈ T0 is selected arbitrarily, then substituting T with t in (13) yields the desired inequality (3).
Remark 2.1: Since T is an arbitrary time scale, then if we take T for some peculiar cases in Theorem 2.1, then we can obtain some corollaries immediately. Especially, if T = R, t0 = 0, then Theorem 2.1 reduces to [[17], Theorem 2.2], which is the continuous result. However, if we take T = Z, we obtain the discrete result, which is given in the following corollary.
Corollary 2.1: Suppose T = Z, n0 ∈ Z, and Z0 = [n0, ∞) ∩ Z. u, a, b, f ∈ (Z0, R+), and a, b are decreasing on Z0. τ ∈ (Z0, Z), τ (n) ≤ n, -∞ < α = inf{τ(n), n ∈ Z0} ≤ n0, ϕ ∈ C rd ([α, n0] ∩ Z, R+). ω is defined the same as in Theorem 2.1. If for n ∈ Z0, u(n) satisfies

with the initial condition

then

In Theorem 2.1, if we change the conditions for a, b, ω p; then, we can obtain another bound for the function u(t).
Theorem 2.2: Suppose u, a, b, f ∈ C rd (T0, R+), ω ∈ C(R+, R+) is nondecreasing, subadditive, and submultiplicative, that is, for ∀α ≥ 0, β ≥ 0 we always have ω(α + β) ≤ ω(α) + ω (β) and ω(αβ) ≤ ω(α)ω(β). τ, α, ϕ are the same as in Theorem 2.1. If u(t) satisfies the inequality (1) with the initial condition (2), then for ∀K > 0, we have

where  is an increasing bijective function, and
is an increasing bijective function, and

Proof: Let

Then,

Similar to the process of (7)-(9), we have

Considering ω is nondecreasing, subadditive, and submultiplicative, Combining (16), (18), and Lemma 2.1, we obtain

where A(t) is defined in (15).
Let T be fixed in T0, and t ∈ [t0, T] ⋂ T. Denote

Considering A(t) is nondecreasing, then we have

Furthermore,

Similar to Theorem 2.1, we have

Substituting t with s in (22), and an integration with respect to s from t0 to t yields

which is followed by

Combining (17), (21), and (23), we obtain

Taking t = T in (24), yields

Since T is selected from T0 arbitrarily, then substituting T with t in (25), we can obtain the desired inequality (14).
Remark 2.2: Theorem 2.2 unifies some known results in the literature. If we take T = R, t0 = 0, τ(t) = t, K = 1, then Theorem 2.2 reduces to [[18], Theorem 2(b3)], which is one case of continuous inequality. If we take T = Z, t0 = 0, τ(t) = t, K = 1, then Theorem 2.2 reduces to [[18], Theorem 4(d3)], which is the discrete analysis of [[18], Theorem 2(b3)].
Now we present a more general result than Theorem 2.1. We study the following delay integral inequality on time scales.

where u, a, b, f, g, h ∈ Crd(T0, R+), ω ∈ C(R+, R+), and a, b, ω are nondecreasing, η ∈ C(R+, R+) is increasing, τ i ∈ (T0, T) with τ i (t) ≤ t, i = 1, 2, and -∞ < α = inf{min{τ i (t), i = 1, 2}, t ∈ T0} ≤ t0.
Theorem 2.3: Define a bijective function  such that
such that  , with
, with  . If
. If  is increasing, and for t ∈ T0, u(t) satisfies the inequality (26) with the initial condition
is increasing, and for t ∈ T0, u(t) satisfies the inequality (26) with the initial condition

where ϕ ∈ C rd ([α, t0] ⋂ T, R+), then

Proof: Let the right side of (26) be v(t), then

For t ∈ T0, if τ i (t) ≥ t0, considering τ i (t) ≤ t, then τ i (t) ∈ T0, and from (29), we have

If τ i (t) ≤ t0, from (27), we obtain

So from (30) and (31), we always have

Furthermore, considering η is increasing, we get that

Fix a T ∈ T0, and let t ∈ [t0, T] ⋂ T. Define

Since a, b are nondecreasing on T0, it follows that

On the other hand,

Similar to Theorem 2.1, we have

Replacing t with s, and an integration for (36) with respect to s from t0 to t yields

Since c(t0) = a(T), and G is increasing, it follows that

Combining (29), (35), (38), we have

Taking t = T in (39), yields

Since T ∈ T0 is selected arbitrarily, then substituting T with t in (40) yields the desired inequality (28).
Remark 2.3: If we take η(u) = up, g(t) ≡ 0, then Theorem 2.3 reduces to Theorem 2.1.
Next, we consider the delay integral inequality of the following form.

where u, f, g, h, a, τ i , i = 1, 2 are the same as in Theorem 2.3, m ∈ C(R+, R+), p > 0 is a constant, ω ∈ C(R+, R+) is nondecreasing, and ω is submultitative, that is, ω(αβ) ≤ ω(α)ω(β) holds for ∀α ≥ 0, β ≥ 0.
Theorem 2.4: Suppose G ∈ (R+, R) is an increasing bijective function defined as in Theorem 2.1. If u(t) satisfies, the inequality (41) with the initial condition

then

Proof: Let the right side of (41) be v(t). Then,

and similar to the process of (30)-(32) we have

Furthermore,

A suitable application of Lemma 2.2 to (46) yields

Fix a T ∈ T0, and let t ∈ [t0, T] ⋂ T. Define

Then,

and

Similar to Theorem 2.1, we have

An integration for (50) from t0 to t yields

Considering G is increasing and  , it follows
, it follows

Combining (44), (49), and (51), we have

Taking t = T in (52), yields

Since T ∈ T0 is selected arbitrarily, after substituting T with t in (53), we obtain the desired inequality (43).
Remark 2.4: If we take ω(u) = u, τ1(t) = t, h(t) ≡ 0, then Theorem 2.4 reduces to [[11], Theorem 3]. If we take m(t) = f(t) = h(t) ≡ 0, then Theorem 2.4 reduces to Theorem 2.1 with slight difference.
Finally, we consider the following integral inequality on time scales.

where u, f, g, ω, τ1, τ2 are the same as in Theorem 2.3, p, q, C are constants, and p > q > 0, C > 0.
Theorem 2.5: If u(t) satisfies (54) with the initial condition (42), then

where  , H are two increasing bijective functions, and
, H are two increasing bijective functions, and

Proof: Let the right side of (54) be v(t). Then,

and similar to the process of (30)-(32) we have

Furthermore,

Similar to Theorem 2.1, we have

An integration for (59) from t0 to t yields

Considering  is increasing, and v(t0) = C, then (60) implies
is increasing, and v(t0) = C, then (60) implies

Given a fixed number T in T0, and t ∈ [t0, T]. Let

Then,

and furthermore,

that is,

Integrating (64) from t0 to t yields

Since H is increasing, and  , then (65) implies
, then (65) implies

Combining (57), (63), and (66), we obtain

Taking t = T in (67), and since T is an arbitrary number in T0, then the desired inequality can be obtained after substituting T with t.
Remark 2.5: If we take T = R, τ1(t) = τ2(t), then we can obtain a new bound of for the unknown continuous function u(t), which is different from the result using the method in [[19], Theorem 2.1].
Remark 2.6: If we take T = R in Theorem 2.3-2.4, or take T = Z in Theorem 2.3-2.5, then immediately we obtain a number of corollaries on continuous and discrete analysis, which are omitted here.
3 Applications
In this section, we will present some applications for the established results above. Some new bounds for solutions of certain dynamic equations on time scales will be derived in the following examples.
Example 1: Consider the delay dynamic integral equation on time scales

with the initial condition

where u ∈ C rd (T0, R), C = up(t0), p is a positive number with p ≥ 1, τ, α are defined as in Theorem 2.1, ϕ ∈ C rd ([α, t0] ⋂ T, R).
Theorem 3.1 Suppose, u(t) is a solution of (68) and assumes |F(t, u)| ≤ f(t)|u|, where f ∈ C rd (T0, R+), then we have

where

Proof: From (68), we obtain

Let ω ∈ C(R+, R+), and ω(v) = v. Then, (72) can be rewritten as

A suitable application of Theorem 2.1 to (73) yields the desired inequality.
Remark 3.1: In the proof for Theorem 3.1, if we apply Theorem 2.2 instead of Theorem 2.1 to (73), then we obtain another bound for u(t) as follows.

where K > 0 ia an arbitrary constant, and

Example 2: Consider the following delay dynamic differential equation on time scales

with the initial condition

where u ∈ C rd (T0, R), C = up(t0), p is a positive number with p ≥ 1, α, τ i , i = 1, 2 are defined as in Theorem 2.3, ϕ ∈ C rd ([α, t0] ⋂ T, R).
Theorem 3.2: Suppose u(t) is a solution of (76), and assume |F(t, u, v)| ≤ f(t)|u| + |v|, |M(t, u)| ≤ h(t)|u|, where f, h ∈ C rd (T0, R+), then have

where G is defined as in Theorem 3.1.
Proof: The equivalent integral form of (75)-(76) can be denoted by

Then,

where ω ∈ C (R+, R+), and ω(u) = u.
A suitable application of Theorem 2.3 to (79) yields the desired inequality.
4 Conclusions
In this paper, some new integral inequalities on time scales have been established. As one can see through the present examples, the established results are useful in dealing with the boundedness of solutions of certain delay dynamic equations on time scales. Finally, we note that the process of Theorem 2.1-2.5 can be applied to establish delay integral inequalities with two independent variables on time scales.
References
Hilger S: Analysis on measure chains-a unified approach to continuous and discrete calculus. Results Math 1990, 18: 18–56.
Bohner M, Erbe L, Peterson A: Oscillation for nonlinear second order dynamic equations on a time scale. J Math Anal Appl 2005,301(2):491–507. 10.1016/j.jmaa.2004.07.038
Xing Y, Han M, Zheng G: Initial value problem for first-order integro-differential equation of Volterra type on time scales. Nonlinear Anal.: Theory Methods Appl 2005,60(3):429–442.
Agarwal RP, Bohner M, O'Regan D, Peterson A: Dynamic equations on time scales: a survey. J Comput Appl Math 2006,141(1–2):1–26.
Wong FH, Yeh CC, Lian WC: An extension of Jensen's inequality on time scales. Adv Dyn Syst Appl 2006,1(1):113–120.
Cheng XL: Improvement of some Ostrowski-Grüss type inequalities. Comput Math Appl 2001, 42: 109–114. 10.1016/S0898-1221(01)00135-3
Bohner M, Matthews T: The Grüss inequality on time scales. Commun Math Anal 2007,3(1):1–8.
Ngô QA: Some mean value theorems for integrals on time scales. Appl Math Comput 2009, 213: 322–328. 10.1016/j.amc.2009.03.025
Liu WJ, Ngô QA: Some Iyengar-type inequalities on time scales for functions whose second derivatives are bounded. Appl Math Compu 2010, 216: 3244–3251. 10.1016/j.amc.2010.04.049
Liu WJ, Ngô QA: A generalization of Ostrowski inequality on time scales for k points. Appl Math Comput 2008, 203: 754–760. 10.1016/j.amc.2008.05.124
Li WN: Some delay integral inequalities on time scales. Comput Math Appl 2010, 59: 1929–1936. 10.1016/j.camwa.2009.11.006
Ma QH, Pečarić J: The bounds on the solutions of certain two-dimensional delay dynamic systems on time scales. Comput Math Appl 2011, 61: 2158–2163. 10.1016/j.camwa.2010.09.001
Li WN: Some new dynamic inequalities on time scales. J Math Anal Appl 2006, 319: 802–814. 10.1016/j.jmaa.2005.06.065
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston; 2001.
Jiang FC, Meng FW: Explicit bounds on some new nonlinear integral inequality with delay. J Comput Appl Math 2007, 205: 479–486. 10.1016/j.cam.2006.05.038
Agarwal R, Bohner M, Peterson A: Inequalities on time scales: a survey. Math Inequal Appl 2001,4(4):535–557.
Lipovan O: Integral inequalities for retarded Volterra equations. J Math Anal Appl 2006, 322: 349–358. 10.1016/j.jmaa.2005.08.097
Pachpatte BG: On some new inequalities related to a certain inequality arising in the theory of differential equations. J Math Anal Appl 2000, 251: 736–751. 10.1006/jmaa.2000.7044
Sun YG: On retarded integral inequalities and their applications. J Math Anal Appl 2005, 301: 265–275. 10.1016/j.jmaa.2004.07.020
Acknowledgements
This work is supported by National Natural Science Foundation of China (11026047 and 10571110), Natural Science Foundation of Shandong Province (ZR2009AM011, ZR2010AQ026, and ZR2010AZ003) (China) and Specialized Research Fund for the Doctoral Program of Higher Education (20103705 110003)(China). The authors thank the referees very much for their careful comments and valuable suggestions on this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
5 Competing interests
The authors declare that they have no competing interests.
6 Authors' contributions
QF carried out the main part of this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feng, Q., Meng, F., Zhang, Y. et al. Some nonlinear delay integral inequalities on time scales arising in the theory of dynamics equations. J Inequal Appl 2011, 29 (2011). https://doi.org/10.1186/1029-242X-2011-29
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-29


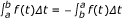

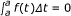
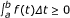 .
.