Skip to main content
Journal of Inequalities and Applications
Download PDF

On the Krasnoselskii-type fixed point theorems for the sum of continuous and asymptotically nonexpansive mappings in Banach spaces

Journal of Inequalities and Applications volume 2011, Article number: 28 (2011) Cite this article

Abstract

In this article, we prove some results concerning the Krasnoselskii theorem on fixed points for the sum A + B of a weakly-strongly continuous mapping and an asymptotically nonexpansive mapping in Banach spaces. Our results encompass a number of previously known generalizations of the theorem.

1 Introduction

As is well known, Krasnoselskii's fixed point theorem has a wide range of applications to nonlinear integral equations of mixed type (see [1]). It has also been extensively employed to address differential and functional differential equations. His theorem actually combines both the Banach contraction principle and the Schauder fixed point theorem, and is useful in establishing existence theorems for perturbed operator equations. Since then, there have appeared a large number of articles contributing generalizations or modifications of the Krasnoselskii fixed point theorem and their applications (see [2]-[21]).

The study of asymptotically nonexpansive mappings concerning the existence of fixed points have become attractive to the authors working in nonlinear analysis. Goebel and Kirk [22] introduced the concept of asymptotically nonexpansive mappings in Banach spaces and proved a theorem on the existence of fixed points for such mappings in uniformly convex Banach spaces. In 1971, Cain and Nashed [23] generalized to locally convex spaces a well known fixed point theorem of Krasnoselskii for a sum of contraction and compact mappings in Banach spaces. The class of asymptotically nonexpansive mappings includes properly the class of nonexpansive mappings as well as the class of contraction mappings. Recently, Vijayaraju [21] proved by using the same method some results concerning the existence of fixed points for a sum of nonexpansive and continuous mappings and also a sum of asymptotically nonexpansive and continuous mappings in locally convex spaces. Very recently, Agarwal et al. [1] proved some existence theorems of a fixed point for the sum of a weakly-strongly continuous mapping and a nonexpansive mapping on a Banach space and under Krasnoselskii-, Leray Schauder-, and Furi-Pera-type conditions.

Motivated and inspired by Agarwal et al. [1] and Vijayaraju [21], in this article we will prove some new generalized forms of the Krasnoselskii theorem on fixed points for the sum A + B of a weakly-strongly continuous mapping and an asymptotically nonexpansive mapping in Banach spaces. These results encompass a number of previously known generalizations of the theorem.

2 Preliminaries

Let M be a nonempty subset of a Banach space X and T : M → X be a mapping. We say that T is weakly-strongly continuous if for each sequence {x n } in M which converges weakly to x in M, the sequence {Tx n } converges strongly to Tx. The mapping T is nonexpansive if ||Tx -Ty|| ≤ ||x - y|| for all x, y ∈ M, and T is asymptotically nonexpansive (see [22]) if there exists a sequence {k n } with k n ≥ 1 for all n and limn→∞k n = 1 such that ||Tnx - Tny|| ≤ k n ||x - y|| for all n ≥ 1 and x, y ∈ M.

Definition 2.1. [21] If B and A map M into X, then B is called a uniformly asymptotically regular with respect to A if, for each ε > 0 there exists n0 ∈ ℕ, such that

for all n ≥ n0 and all x ∈ M.

Now, let us recall some definitions and results which will be needed in our further considerations. Let X be a Banach space, Ω(X) is the collection of all nonempty bounded subsets of X, and is the subset of Ω(X) consisting of all weak compact subsets of X. Let B r denote the closed ball in X countered at 0 with radius r > 0. In [24], De Blasi introduced the following mapping ω : Ω(X) → [0, ∞) defined by

for all M ∈ Ω(X). For completeness, we recall some properties of ω(·) needed below (for the proofs we refer the reader to [24]).

Lemma 2.2. [24] Let M1 and M2 ∈ Ω(X), then we have

(i) If M1 ⊆ M2, then ω(M1) ≤ ω(M2).

(ii) ω(M1) = 0 if and only if M1 is relatively weakly compact.

(iii) , where is the weak closure of M1.

(iv) ω(λM1) = |λ|ω(M1) for all λ ∈ ℝ.

(v) ω(co(M1)) = w(M1).

(vi) ω(M1 + M2) ≤ ω(M1) + ω(M2).

(vii) If (M n )n≥1is a decreasing sequence of nonempty, bounded and weakly closed subsets of X with limn→∞ω(M n ) = 0, then and , i.e., is relatively weakly compact.

Throughout this article, a measure of weak noncompactness will be a mapping ψ : Ω(X) → [0, ∞) which satisfies the assumptions (i)-(vii) cited in Lemma 2.2.

Definition 2.3. [25] Let M be a closed subset of X and I, T : M → M be two mappings. A mapping T is said to be demiclosed at the zero, if for each sequence {x n } in M, the conditions x n → x0 weakly and Tx n → 0 strongly imply Tx0 = 0.

Lemma 2.4. [26]-[29] Let X be a uniformly convex Banach space, M be a nonempty closed convex subset of X, and let T : M → M be an asymptotically nonexpansive mapping with F(T) ≠ ∅. Then I - T is demiclosed at zero, i.e., for each sequence {x n } in M, if {x n } converges weakly to q ∈ M and {(I - T)x n } converges strongly to 0, then (I - T)q = 0.

Definition 2.5. [1, 13] Let X be a Banach space and let ψ be a measure of weak noncompactness on X. A mapping B : D(B) ⊆ X → X is said to be ψ-contractive if it maps bounded sets into bounded sets and there is a β ∈ [0, 1) such that ψ(B(S)) ≤ βψ(S) for all bounded sets S ⊆ D(B). The mapping B : D(B) ⊆ X → X is said to be ψ-condensing if it maps bounded sets into bounded sets and ψ(B(S)) < ψ(S) whenever S is a bounded subset of D(B) such that ψ(S) > 0.

Let 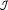be a nonlinear operator from into X. In the next section, we will use the following two conditions:

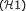
If (x n )n∈ℕis a weakly convergent sequence in , then has a strongly convergent subsequence in X.

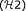
If (x n )n∈ℕis a weakly convergent sequence in , then has a weakly convergent subsequence in X.

Remark 2.6. 1. Operators satisfying 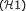or 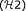are not necessarily weakly continuous (see [12, 19, 30]).

  1. 2.

    Every w-contractive mapping satisfies .

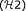  2. 3.

    A mapping 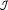satisfies 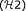if and only if it maps relatively weakly compact sets into relatively weakly compact ones (use the Eberlein-Š mulian theorem [31]).

  3. 4.

    A mapping 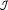satisfies 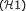if and only if it maps relatively weakly compact sets into relatively compact ones.

  4. 5.

    The condition 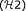holds true for every bounded linear operator.

The following fixed point theorems are crucial for our purposes.

Lemma 2.7. [12] Let M be a nonempty closed bounded convex subset of a Banach space X. Suppose that A : M → X and B : X → X satisfying:

(i) A is continuous, AM is relatively weakly compact and A satisfies ,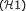

(ii) B is a strict contraction satisfying ,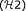

(iii) Ax + By ∈ M for all x, y ∈ M.

Then, there is an x ∈ M such that Ax + Bx = x.

Lemma 2.8. [20] Let M be a nonempty closed bounded convex subset of a Banach space X. Suppose that A : M → X and B : M → X are sequentially weakly continuous such that:

(i) AM is relatively weakly compact,

(ii) B is a strict contraction,

(iii) Ax + By ∈ M for all x, y ∈ M.

Then, there is an x ∈ M such that Ax + Bx = x.

Lemma 2.9. [1] Let X be a Banach space and let ψ be measure of weak noncompactness on X. Let Q and C be closed, bounded, convex subset of X with Q ⊆ C. In addition, let U be a weakly open subset of Q with 0 ∈ U, and a weakly sequentially continuous and ψ-condensing mapping. Then either

(2.1)

or

(2.2)

here ∂ Q U is the weak boundary of U in Q.

Lemma 2.10. [1] Let X be a Banach space and B : X → X a k-Lipschitzian mapping, that is

In addition, suppose that B verifies 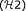. Then for each bounded subset S of X, we have ψ(BS) ≤ kψ(S);

here,ψ is the De Blasi measure of weak noncompactness.

Lemma 2.11. [15, 32] Let X be a Banach space with C ⊆ X closed and convex. Assume U is a relatively open subset of C with 0 ∈ U, bounded and a condensing mapping. Then, either F has a fixed point in or there is a point u ∈ ∂U and λ ∈ (0,1) with u = λF(u); here and ∂U denote the closure of U in C and the boundary of U in C, respectively.

Lemma 2.12. [15, 32] Let X be a Banach space and Q a closed convex bounded subset of X with 0 ∈ Q. In addition, assume F : Q → X a condensing mapping with if is a sequence in ∂Q× [0, 1] converging to (x, λ) with X = λF(x) and 0 < λ < 1, then λ j F (x j ) ∈ Q for j sufficiently large, holding. Then F has a fixed point.

3 Main results

Now, we are ready to state and prove the main result of this section.

Theorem 3.1. Let M be a nonempty bounded closed convex subset of a Banach space X. Let A : M → X and B : M → M satisfy the following:

(i) A is weakly-strongly continuous, and AM is relatively weakly compact,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞) satisfying ,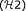

(iii) if (x n ) is a sequence of M such that ((I - B)x n ) is weakly convergent, then the sequence (x n ) has a weakly convergent subsequence,

(iv) I - B is demiclosed,

(v) Bnx + Ay ∈ M for all x, y ∈ M and n = 1, 2,...,

(vi) B is uniformly asymptotically regular with respect to A.

Then, there is an x ∈ M such that Ax + Bx = x.

Proof. Suppose first that 0 ∈ M and let for all n ∈ ℕ. By hypothesis (v), we have

Since B is asymptotically nonexpansive, it follows that

(3.1)

Hence, a n Bn is contraction on M. Therefore, by Lemma 2.7, there is an x n ∈ M such that

(3.2)

for all n ∈ ℕ. This implies that

(3.3)

since a n → 1 as n → ∞ and M is bounded and Bnx + Ay ∈ M for all x, y ∈ M. Since B is uniformly asymptotically regular with respect to A, it follows that

(3.4)

From (3.3) and (3.4), we obtain

(3.5)

Now, it is noted that

(3.6)

Using (3.3) and (3.5) in (3.6), we get

(3.7)

Using the fact that AM is weakly compact and passing eventually to a subsequence, we may assume that {Ax n } converges weakly to some y ∈ M. By (3.7), we have

(3.8)

By hypothesis (iii), the sequence {x n } has a subsequence which converges weakly to some x ∈ M. Since A is weakly-strongly continuous, converges strongly to Ax.

Hence, we observe that

(3.9)

Hence, by the demiclosedness of I - B, we have Ax + Bx = x.

To complete the proof, it remains to consider the case 0 ∉ M. In such a case, let us fix any element x0 ∈ M and let M0 = {x - x0, x ∈ M }. Define two mappings A0 : M0 → X and B0 : M0 → M by and , for x ∈ M. By the result of the first case for A0 and B0, we have an x ∈ M such that A0(x - x0) + B0(x - x0) = x - x0. Hence Ax + Bx = x. □

Corollary 3.2. Let M be a nonempty bounded closed convex subset of a uniformly convex Banach space X. Let A : M → X and B : M → M satisfy the following:

(i) A is weakly-strongly continuous,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞),

(iii) Bnx + Ay ∈ M for all x, y ∈ M, and n = 1, 2,...,

(iv) B is uniformly asymptotically regular with respect to A.

Then, there is an x ∈ M such that Ax + Bx = x.

Our next result is the following:

Theorem 3.3. Let M be a nonempty bounded closed convex subset of a Banach space X. Suppose that A : M → X and B : M → M are two weakly sequentially continuous mappings that satisfy the following:

(i) AM is relatively weakly compact,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞),

(iii) if (x n ) is a sequence of M such that ((I - B)x n ) is weakly convergent, then the sequence (x n ) has a weakly convergent subsequence,

(iv) Bnx + Ay ∈ M for all x, y ∈ M, and n = 1, 2,...,

(v) B is uniformly asymptotically regular with respect to A.

Then, there is an x ∈ M such that Ax + Bx = x.

Proof. Without loss of generality, we may assume that 0 ∈ M. Let for all n ∈ ℕ. By hypothesis (iv), we have

Since B is asymptotically nonexpansive, it follows that

(3.10)

Hence, a n Bn is a contraction on M. By Lemma 2.8, there is a x n ∈ M such that

(3.11)

for all n ∈ ℕ. This implies that

(3.12)

Since B is uniformly asymptotically regular with respect to A, it follows that

(3.13)

From (3.12) and (3.13), we obtain

(3.14)

Now, it is noted that

(3.15)

Using (3.12) and (3.14) in (3.15), we get

(3.16)

Using the fact that AM is weakly compact and passing eventually to a subsequence, we may assume that {Ax n } converges weakly to some y ∈ M. Hence, by (3.16)

(3.17)

By hypothesis (iii), the sequence {x n } has a subsequence which converges weakly to some x ∈ M. Since A and B are weakly sequentially continuous, converges weakly to Ax, and converges weakly to Bx. Hence, Ax + Bx = x. □

Theorem 3.4. Let Q and C be closed bounded convex subset of a Banach space X with Q ⊆ C. In addition, let U be a weakly open subset of Q with 0 ∈ U, and B : X → X are two weakly sequentially continuous mappings satisfying the following:

(i) is a relatively weakly compact,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞),

(iii) if (x n ) is a sequence of M such that ((I - B)x n ) is weakly convergent, then the sequence (x n ) has a weakly convergent subsequence,

(iv) Bnx + Ay ∈ C for all , and n = 1, 2,...,

(v) B is uniformly asymptotically regular with respect to A.

Then, either

(3.18)

or

(3.19)

here, ∂ Q U is the weak boundary of U in Q.

Proof. Let for all n ∈ ℕ. We first show that the mapping F n = a n A+a n Bn is ψ-contractive with constant a n . To see that, let S be a bounded subset of . Using the homogeneity and the subadditivity of the De Blasi measure of weak noncompactness, we obtain

Keeping in mind that A is weakly compact and using Lemma 2.10, we deduce that

This proves that F n is ψ-contractive with constant a n . Moreover, taking into account that 0 ∈ U and using assumption (iv), we infer that F n map into C. Next, we suppose that (3.19) does not occur, and F n does not have a fixed point on ∂ Q U (otherwise we are finished since (3.18) occurs). If there exists a u ∈ ∂ Q U, and λ ∈ (0, 1) with u = λF n u then u = λa n Au + λa n Bnu. It is impossible since λa n ∈ (0, 1). By Lemma 2.9, there exists such that

for all n ∈ ℕ. This implies that

(3.20)

Since B is uniformly asymptotically regular with respect to A, it follows that

(3.21)

From (3.20) and (3.21), we obtain

(3.22)

Now, it is noted that

(3.23)

Using (3.20) and (3.22) in (3.23), we get

(3.24)

Since AM is weakly compact and passing eventually to a subsequence, we may assume that {Ax n } converges weakly to some . Thus, we have

(3.25)

By hypothesis (iii), the sequence {x n } has a subsequence which converges weakly to some . Since A and B are weakly sequentially continuous, converges weakly to Ax, and converges weakly to Bx. Hence, Ax + Bx = x. □

Theorem 3.5. Let U be a bounded open convex set in a Banach space X with 0 ∈ U. Suppose and B : X → X are continuous mappings satisfying the following:

(i) is compact, and A is weakly-strongly continuous,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞), and I - B is demiclosed,

(iii) if (x n ) is a sequence of such that ((I - B)x n ) is weakly convergent, then the sequence (x n ) has a weakly convergent subsequence,

(iv) B is uniformly asymptotically regular with respect to A.

Then, either

(3.26)

or

(3.27)

Proof. Suppose (3.27) does not occur and let for all n ∈ ℕ. The mapping F n := a n A + a n Bn is the sum of a compact and a strict contraction. This implies that F n is a condensing mapping (see [13]). By Lemma 2.11, we deduce that there is an such that

for all n ∈ ℕ. This implies that

(3.28)

Since B is uniformly asymptotically regular with respect to A, it follows that

(3.29)

From (3.28) and (3.29), we obtain

(3.30)

Now, it is noted that

(3.31)

Using (3.28) and (3.30) in (3.31), we get

(3.32)

Since AM is weakly compact and passing eventually to a subsequence, we may assume that {Ax n } converges weakly to some . This implies that

(3.33)

By hypothesis (iii), the sequence {x n } has a subsequence which converges weakly to some . Since A is weakly-strongly continuous, converges strongly to Ax.

Consequently

(3.34)

By the demiclosedness of I - B, we have Ax + Bx = x. □

Corollary 3.6. Let U be a bounded open convex set in a uniformly convex Banach space X with 0 ∈ U. Suppose and B : X → X are continuous mappings satisfying the following.

(i) is compact, and A is weakly-strongly continuous,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞),

(iii) B is uniformly asymptotically regular with respect to A.

Then, either

(3.35)

or

(3.36)

Theorem 3.7. Let Q be a closed convex bounded set in a Banach space X with 0 ∈ Q. Suppose A : Q → X and B : X → X are continuous mappings satisfying the following:

(i) A(Q) is compact, and A is weakly-strongly continuous,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞), and I - B is demiclosed,

(iii) if (x n ) is a sequence of such that ((I - B)x n ) is weakly convergent, then the sequence (x n ) has a weakly convergent subsequence,

(iv) if is a sequence of ∂Q × [0, 1] converging to (x, λ) with X = λAx + λBnx and 0 ≤ λ < 1, then λ j Ax j + λ j Bnx j ∈ Q for j sufficiently large,

(v) B is uniformly asymptotically regular with respect to A.

Then, A + B has a fixed point in Q.

Proof. We first define F n := a n A + a n Bn, where for all n ∈ ℕ. Since F n is the sum of a compact mapping and a strict contraction mapping, it follows that F n is a condensing mapping. For any let fixed n, we have is a sequence of ∂Q × [0, 1] converging to (y, λ) with y = λF n (y) and 0 ≤ λ < 1. Then y = a n λAy + a n λBny. From assumption (iv), it follows that a n λ j Ay j + a n λ j Bny j ∈ Q for j sufficiently large. Applying Lemma 2.12 to F n , we deduce that there is an x n ∈ Q such that

As in Theorem 3.5 this implies that

(3.37)

By hypothesis (iii), the sequence {x n } has a subsequence which converges weakly to some x ∈ Q. Since A is weakly-strongly continuous, converges strongly to Ax.

It follows that

(3.38)

Hence, by the demiclosedness of I - B, we have Ax + Bx = x. □

Corollary 3.8. Let Q be a closed convex bounded set in a uniformly convex Banach space X with 0 ∈ Q. Suppose A : Q → X and B : X → X are continuous mappings satisfying the following:

(i) A(Q) is compact and A is weakly-strongly continuous,

(ii) B is an asymptotically nonexpansive mapping with a sequence (k n ) ⊂ [1, ∞),

(iii) if is a sequence of ∂Q × [0, 1] converging to (x, λ) with X = λAx + λBnx and 0 ≤ λ < 1, then λ j Ax j + λ j Bnx j ∈ Q for j sufficiently large,

(iv) B is uniformly asymptotically regular with respect to A.

Then, A + B has a fixed point in Q.

References

  1. Agarwal RP, O'Regan D, Taoudi MA: Browder-Krasnoselskii type fixed point theorem in Banach space. Fixed Point Theory Appl 2010.

    Google Scholar 

  2. Agarwal RP, Mehan M, O'Regan D: Fixed Point Theory and Applications. Cambridge University Press, Cambridge; 2001.

    Chapter  Google Scholar 

  3. Barroso CS: Krasnoselskii's fixed point theorem for weakly continuous maps. Nonlinear Anal 2003, 55: 25–31. 10.1016/S0362-546X(03)00208-6

    Article  MathSciNet  Google Scholar 

  4. Barroso CS, Teixeira EV: A topological and geometric approach to fixed point results for sum of operators and applications. Nonlinear Anal 2005, 60: 625–650. 10.1016/j.na.2004.09.040

    Article  MathSciNet  Google Scholar 

  5. Ben Amar A, Jeribi A, Mnif M: On a generalization of the Schauder and Krasnosel'skii fixed point theorems on Dunford-Pettis space and applications. Math Methods Appl Sci 2005, 28: 1737–1756. 10.1002/mma.639

    Article  MathSciNet  Google Scholar 

  6. Burtun TA: A fixed point theorem of Krasnoselskii. Appl Math Lett 1998, 11: 85–88.

    Article  Google Scholar 

  7. Burton TA, Furumochi T: Krasnoselskii's fixed point theorem and stability. Nonlinear Anal 2002, 49: 445–454. 10.1016/S0362-546X(01)00111-0

    Article  MathSciNet  Google Scholar 

  8. Fucik S: Fixed point theorems for sum of nonlinear mappings. Commentationes Mathematicae Universitatis Carolinae 1968, 9: 133–143.

    MathSciNet  Google Scholar 

  9. Krasnoselskii MA: Two remarks on the method of successive approximations. Uspekhi Math Nauk 1955, 10: 123–127.

    MathSciNet  Google Scholar 

  10. Krasnoselskii MA: Topological Methods in the Theory of Nonlinear Integral Equations. Pergamon Press, New York; 1964.

    Google Scholar 

  11. Krasnoselskii MA, Zabrejko PP, Pustyl'nik JI, Sobolevskii JI: Integral Operators in Spaces of Summable Functions. Nauka, Moscow; 1966.

    Google Scholar 

  12. Latrach K, Taoudi MA, Zeghal A: Some fixed point theorems of the Schauder and Krasnosel'skii type and application to nonlinear transport equations. J Diff Equ 2006, 221: 256–271. 10.1016/j.jde.2005.04.010

    Article  MathSciNet  Google Scholar 

  13. O'Regan D: Fixed point theory for the sum of two operators. Appl Math Lett 1996, 9: 1–8.

    Article  Google Scholar 

  14. O'Regan D: Fixed point theory for weakly sequentially continuous mappings. Math Comput Model 1998, 27: 1–14.

    Article  Google Scholar 

  15. O'Regan D: A fixed point theorems for condensing operators and applications to Hammerstein integral equations in Banach spaces. Comput Math Appl 1995, 30: 39–49.

    Article  Google Scholar 

  16. Park S: Generalizations of the Krasnoselskii fixed point theorem. Nonlinear Anal 2007, 67: 3401–3410. 10.1016/j.na.2006.10.024

    Article  MathSciNet  Google Scholar 

  17. Reinermann J: Fixpunktsatze vom Krasnoselskii-typ. Math Z 1971, 119: 339–344. 10.1007/BF01109885

    Article  MathSciNet  Google Scholar 

  18. Singh SP: Fixed point theorems fora sum of nonlinear operators. Rend Accad Naz Lincei 1973, 54: 1–4.

    Google Scholar 

  19. Taoudi MA: Integrable solutions of a nonlinear functional integral equation on an unbounded interval. Nonlinear Anal 2009, 71: 4131–4136. 10.1016/j.na.2009.02.072

    Article  MathSciNet  Google Scholar 

  20. Taoudi MA: Krasnosel'skii type fixed point theorems under weak topology features. Nonlinear Anal 2010, 72: 478–482. 10.1016/j.na.2009.06.086

    Article  MathSciNet  Google Scholar 

  21. Vijayaraju P: Fixed point theorems for a sum of two mappings in locally convex spaces. Int J Math Math Sci 1994, 17: 681–686. 10.1155/S0161171294000967

    Article  MathSciNet  Google Scholar 

  22. Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proc Am Math Soc 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3

    Article  MathSciNet  Google Scholar 

  23. Cain GL, Nashed MZ: Fixed points and stability for a sum of two operators in locally convex spaces. Pacific J Math 1971, 39: 581–592.

    Article  MathSciNet  Google Scholar 

  24. De Blasi FS: On a property of the unit sphere in Banach spaces. Bull Math Soc Sci Math Roum 1977, 21: 259–262.

    MathSciNet  Google Scholar 

  25. Gu F: Some convergence theorems of non-implicit iteration process with errors for a finite families of I -asymptotically nonexpansive mappings. Appl Math Comput 2010, 216: 161–172. 10.1016/j.amc.2010.01.025

    Article  MathSciNet  Google Scholar 

  26. Chang SS, Cho YJ: The implicit iterative processes for asymptotically nonexpansive mappings. Nonlinear Funct Anal Appl 2003, 1: 369–382.

    MathSciNet  Google Scholar 

  27. Chidume CE, Ofoedu EU, Zegeye H: Strong and weak convergence thorems for asymptotically nonexpansive mappings. J Mathods Anal Appl 2003, 280: 364–374. 10.1016/S0022-247X(03)00061-1

    Article  MathSciNet  Google Scholar 

  28. Gornicki J: Weak convergence theorems for asymptotically nonexpansive mappings in uniformly convex Banach spaces. Comment Math Univ Carolin 1989, 301: 249–252.

    MathSciNet  Google Scholar 

  29. Tan KK, Xu HK: The nonlinear ergodic theorem for asymptotically nonexpansive mappings in Banach spaces. Proc Am Math Soc 1992, 114: 399–404. 10.1090/S0002-9939-1992-1068133-2

    Article  MathSciNet  Google Scholar 

  30. Latrach K, Taoudi MA: Existence results for a generalized nonlinear Hammerstein equation on L 1 space. Nonlinear Anal 2007, 66: 2325–2333. 10.1016/j.na.2006.03.022

    Article  MathSciNet  Google Scholar 

  31. Dunford N, Schwartz JT: Linear Operators, Part I: General Theory. Interscience Publishers, New York; 1958.

    Google Scholar 

  32. O'Regan D: Some fixed point theorems for concentrative mappings between locally convex linear topological spaces. Nonlinear Anal 1996, 27: 1437–1446. 10.1016/0362-546X(95)00130-N

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the referee for the insightful comments and suggestions. The first author would like to thanks The Thailand Research Fund for financial support and the second author is also supported by the Royal Golden Jubilee Program under Grant PHD/0282/2550, Thailand. Moreover, the second author the Thailand Research Fund for financial support under Grant BRG5280016.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Naresuan University, Phitsanulok, 65000, Thailand

    Areerat Arunchai & Somyot Plubtieng

Authors
  1. Areerat Arunchai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Somyot Plubtieng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Somyot Plubtieng.

Additional information

Competing interests

The authors declare that they have no competing interests.

Authors' contributions

The work presented here was carried out in collaboration between all authors. SP and AA defined the research theme. SP designed theorems and methods of proof and interpreted the results. AA proved the theorems, interpreted the results and wrote the paper. All authors have contributed to, seen and approved the manuscript.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Arunchai, A., Plubtieng, S. On the Krasnoselskii-type fixed point theorems for the sum of continuous and asymptotically nonexpansive mappings in Banach spaces. J Inequal Appl 2011, 28 (2011). https://doi.org/10.1186/1029-242X-2011-28

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1186/1029-242X-2011-28

Keywords