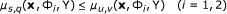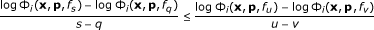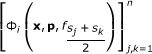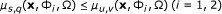- Research
- Open access
- Published:
On the refinements of the Jensen-Steffensen inequality
Journal of Inequalities and Applications volume 2011, Article number: 12 (2011)
Abstract
In this paper, we extend some old and give some new refinements of the Jensen-Steffensen inequality. Further, we investigate the log-convexity and the exponential convexity of functionals defined via these inequalities and prove monotonicity property of the generalized Cauchy means obtained via these functionals. Finally, we give several examples of the families of functions for which the results can be applied.
2010 Mathematics Subject Classification. 26D15.
1. Introduction
One of the most important inequalities in mathematics and statistics is the Jensen inequality (see [[1], p.43]).
Theorem 1.1. Let I be an interval in ℝ and f : I → ℝ be a convex function. Let n ≥ 2, x = (x1, ..., x n ) ∈ In and p = (p1, ..., p n ) be a positive n-tuple, that is, such that p i > 0 for i = 1, ..., n. Then

Where

If f is strictly convex, then inequality (1) is strict unless x1 = ⋯ = x n .
The condition "p is a positive n-tuple" can be replaced by "p is a non-negative n-tuple and P n > 0". Note that the Jensen inequality (1) can be used as an alternative definition of convexity.
It is reasonable to ask whether the condition "p is a non-negative n-tuple" can be relaxed at the expense of restricting x more severely. An answer to this question was given by Steffensen [2] (see also [[1], p.57]).
Theorem 1.2. Let I be an interval in ℝ and f : I → ℝ be a convex function. If x = (x1, ..., x n ) ∈ In is a monotonic n-tuple and p = (p1, ..., p n ) a real n-tuple such that

is satisfied, where P k are as in (2), then (1) holds. If f is strictly convex, then inequality (1) is strict unless x1 = ⋯ = x n .
Inequality (1) under conditions from Theorem 1.2 is called the Jensen-Steffensen inequality. A refinement of the Jensen-Steffensen inequality was given in [3] (see also [[1], p.89]).
Theorem 1.3. Let x and p be two real n-tuples such that a ≤ x1 ≤ ⋯ ≤ x n ≤ b and (3) hold. Then for every convex function f : [a, b] → ℝ

holds, where


P k are as in (2) and

Note that the function G n defined in (6) is in fact the difference of the right-hand and the left-hand side of the Jensen inequality (1).
In this paper, we present a new refinement of the Jensen-Steffensen inequality, related to Theorem 1.3. Further, we investigate the log-convexity and the exponential convexity of functionals defined as differences of the left-hand and the right-hand sides of these inequalities. We also prove monotonicity property of the generalized Cauchy means obtained via these functionals. Finally, we give several examples of the families of functions for which the obtained results can be applied.
In what follows, I is an interval in ℝ, P
k
are as in (2) and  are as in (7). Note that if (3) is valid, since
are as in (7). Note that if (3) is valid, since  , it follows that
, it follows that  satisfy (3) as well.
satisfy (3) as well.
2. New refinement of the Jensen-Steffensen inequality
The aim of this section is to give a new refinement of the Jensen-Steffensen inequality. In the proof of this refinement, the following result is needed (see [[1], p.2]).
Proposition 2.1. If f is a convex function on an interval I and if x1 ≤ y1, x2 ≤ y2, x1 ≠ x2, y1 ≠ y2, then the following inequality is valid

If the function f is concave, the inequality reverses.
The main result states.
Theorem 2.2. Let x = (x1, ..., x n ) ∈ In be a monotonic n-tuple and p = (p1, ..., p n ) a real n-tuple such that (3) holds. Then for a convex function f : I → ℝ we have

where


For a concave function f, the inequality signs in (9) reverse.
Proof. The claim is that for a convex function f,

holds for every k = 2, ..., n. This inequality is equivalent to

where

If x is increasing then  , while if x is decreasing then
, while if x is decreasing then  for every k. Furthermore, without loss of generality, we can assume that x is strictly monotonic and that 0 < P
k
< P
n
for k = 1, ..., n - 1. Now, applying (8) for a convex function f when x is strictly increasing yields inequality
for every k. Furthermore, without loss of generality, we can assume that x is strictly monotonic and that 0 < P
k
< P
n
for k = 1, ..., n - 1. Now, applying (8) for a convex function f when x is strictly increasing yields inequality

while if x is strictly decreasing we get inequality

both of which are equivalent to (12). If f is concave, the inequalities reverse. Thus, the proof is complete. □
Remark 2.3. A slight extension of the proof of Theorem 1.3 in[3]shows that Theorem 1.3 remains valid if the n-tuple x is assumed to be monotonic instead of increasing. The proof is in fact analogous to the proof of Theorem 2.2.
Let us observe inequalities (4) and (9). Motivated by them, we define two functionals


where functions F
k
and  are as in (5) and (10), respectively, x = (x1, ..., x
n
) ∈ In is a monotonic n-tuple and p = (p1, ..., p
n
) is a real n-tuple such that (3) holds. If function f is convex on I, then Theorems 1.3 and 2.2, joint with Remark 2.3, imply that Φ
i
(x, p, f) ≥ 0, i = 1, 2.
are as in (5) and (10), respectively, x = (x1, ..., x
n
) ∈ In is a monotonic n-tuple and p = (p1, ..., p
n
) is a real n-tuple such that (3) holds. If function f is convex on I, then Theorems 1.3 and 2.2, joint with Remark 2.3, imply that Φ
i
(x, p, f) ≥ 0, i = 1, 2.
Now, we give mean value theorems for the functionals Φ i , i = 1, 2.
Theorem 2.4. Let x = (x1, ..., x n ) ∈ [a, b] n be a monotonic n-tuple and p = (p1, ..., p n ) a real n-tuple such that (3) holds. Let f ∈ C2[a, b] and Φ1and Φ2be linear functionals defined as in (13) and (14). Then there exists ξ ∈ [a, b] such that

where f0(x) = x2.
Proof. Analogous to the proof of Theorem 2.3 in [4]. □
Theorem 2.5. Let x = (x1, ..., x n ) ∈ [a, b] n be a monotonic n-tuple and p = (p1, ..., p n ) a real n-tuple such that (3) holds. Let f, g ∈ C2[a, b] be such that g"(x) ≠ 0 for every x ∈ [a, b] and let Φ1and Φ2be linear functionals defined as in (13) and (14). If Φ1and Φ2are positive, then there exists ξ ∈ [a, b] such that

Proof. Analogous to the proof of Theorem 2.4 in [4]. □
Remark 2.6. If the inverse of the function f"/g" exists, then (16) gives

3. Log-convexity and exponential convexity of the Jensen-Steffensen differences
We begin this section by recollecting definitions of properties which are going to be explored here and also some useful characterizations of these properties (see [[5], p.373]). Again, I is an open interval in ℝ.
Definition 1. A function h : I → ℝ is exponentially convex on I if it is continuous and

holds for every n ∈ ℕ, α i ∈ ℝ and x i such that x i + x j ∈ I, i, j = 1, ..., n.
Proposition 3.1. Function h : I → ℝ is exponentially convex if and only if h is continuous and

holds for every n ∈ ℕ, α i ∈ ℝ and x i ∈ I, i = 1, ..., n.
Corollary 3.2. If h is exponentially convex, then the matrix  is a positive semi-definite matrix. Particularly,
is a positive semi-definite matrix. Particularly,

Corollary 3.3. If h : I → (0, ∞) is an exponentially convex function, then h is a log-convex function, that is, for every x, y ∈ I and every λ ∈ [0, 1] we have

Lemma 3.4. A function h : I → (0, ∞) is log-convex in the J-sense on I, that is, for every x, y ∈ I,

holds if and only if the relation

holds for every α, β ∈ ℝ and x, y ∈ I.
Definition 2. The second order divided difference of a function f : [a, b] → ℝ at mutually different points y0, y1, y2 ∈ [a, b] is defined recursively by


Remark 3.5. The value [y0, y1, y2; f] is independent of the order of the points y0, y1and y2. This definition may be extended to include the case in which some or all the points coincide (see [[1], p.16]). Namely, taking the limit y1 → y0in (18), we get

provided that f' exists, and furthermore, taking the limits y i → y0, i = 1, 2, in (18), we get

provided that f″ exists.
Next, we study the log-convexity and the exponential convexity of functionals Φ i (i = 1, 2) defined in (13) and (14).
Theorem 3.6. Let ϒ = {f s : s ∈ I} be a family of functions defined on [a, b] such that the function s ↦ [y0, y1, y2; f s ] is log-convex in J-sense on I for every three mutually different points y0, y1, y2 ∈ [a, b]. Let Φ i (i = 1, 2) be linear functionals defined as in (13) and (14). Further, assume Φ i (x, p, f s ) > 0 (i = 1, 2) for f s ∈ ϒ. Then the following statements hold.
-
(i)
The function s ↦ Φ i (x, p, f s ) is log-convex in J-sense on I.
-
(ii)
If the function s ↦ Φ i (x, p, f s ) is continuous on I, then it is log-convex on I.
-
(iii)
If the function s ↦ Φ i (x, p, f s ) is differentiable on I, then for every s, q, u, v ∈ I such that s ≤ u and q ≤ v, we have
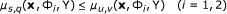 (19)
(19)
where

and Ξ is the family functions f s belong to.
Proof. (i) For α, β ∈ ℝ and s, q ∈ I, we define a function

Applying Lemma 3.4 for the function s ↦ [y0, y1, y2; f s ] which is log-convex in J-sense on I by assumption, yields that

which in turn implies that g is a convex function on I and therefore we have Φ i (x, p, g) ≥ 0 (i = 1, 2). Hence,

Now using Lemma 3.4 again, we conclude that the function s ↦ Φ i (x, p, f s ) is log-convex in J-sense on I.
-
(ii)
If the function s ↦ Φ i (x, p, f s ) is in addition continuous, from (i) it follows that it is then log-convex on I.
-
(iii)
Since by (ii) the function s ↦ Φ i (x, p, f s ) is log-convex on I, that is, the function s ↦ log Φ i (x, p, f s ) is convex on I, applying (8) we get
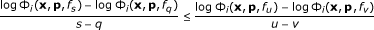 (21)
(21)
for s ≤ u, q ≤ v, s ≠ q, u ≠ v, and therefore conclude that

If s = q, we consider the limit when q → s in (21) and conclude that

The case u = v can be treated similarly. □
Theorem 3.7. Let Ω = {f s : s ∈ I} be a family of functions defined on [a, b] such that the function s ↦ [y0, y1, y2; f s ] is exponentially convex on I for every three mutually different points y0, y1, y2 ∈ [a, b]. Let Φ i (i = 1, 2) be linear functionals defined as in (13) and (14). Then the following statements hold.
-
(i)
If n ∈ ℕ and s 1, ..., s n ∈ I are arbitrary, then the matrix
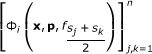
is a positive semi-definite matrix for i = 1, 2. Particularly,

-
(ii)
If the function s ↦ Φ i (x, p, f s ) is continuous on I, then it is also exponentially convex function on I.
-
(iii)
If the function s ↦ Φ i (x, p, f s ) is positive and differentiable on I, then for every s, q, u, v ∈ I such that s ≤ u and q ≤ v, we have
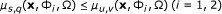 (23)
(23)
where μ s, q (x, Φ i , Ω) is defined in (20).
Proof. (i) Let α j ∈ ℝ (j = 1, ..., n) and consider the function

for n ∈ ℕ, where  , s
j
∈ I, 1 ≤ j, k ≤ n and
, s
j
∈ I, 1 ≤ j, k ≤ n and  . Then
. Then

and since  is exponentially convex by assumption it follows that
is exponentially convex by assumption it follows that

and so we conclude that g is a convex function. Now we have

which is equivalent to

which in turn shows that the matrix  is positive semi-definite, so (22) is immediate.
is positive semi-definite, so (22) is immediate.
-
(ii)
If the function s ↦ Φ i (x, p, f s ) is continuous on I, then from (i) and Proposition 3.1 it follows that it is exponentially convex on I.
-
(iii)
If the function s ↦ Φ i (x, p, f s ) is differentiable on I, then from (ii) it follows that it is exponentially convex on I. If this function is in addition positive, then Corollary 3.3 implies that it is log-convex, so the statement follows from Theorem 3.6 (iii). □
Remark 3.8. Note that the results from Theorem 3.6 still hold when two of the points y0, y1, y2 ∈ [a, b] coincide, say y1 = y0, for a family of differentiable functions f s such that the function s ↦ [y0, y1, y2; f s ] is log-convex in J-sense on I, and furthermore, they still hold when all three points coincide for a family of twice differentiable functions with the same property. The proofs are obtained by recalling Remark 3.5 and taking the appropriate limits. The same is valid for the results from Theorem 3.7.
Remark 3.9. Related results for the original Jensen-Steffensen inequality regarding exponential convexity, which are a special case of Theorem 3.7, were given in[6].
4. Examples
In this section, we present several families of functions which fulfil the conditions of Theorem 3.7 (and Remark 3.8) and so the results of this theorem can be applied for them.
Example 4.1. Consider a family of functions

defined by

We have which shows that g
s
is convex on ℝ for every s ∈ ℝ and
which shows that g
s
is convex on ℝ for every s ∈ ℝ and is exponentially convex by Example 1 given in Jakšetić and Pečarić (submitted). From Jakšetić and Pečarić (submitted), we then also have that s ↦ [y0, y1, y2; g
s
] is exponentially convex.
is exponentially convex by Example 1 given in Jakšetić and Pečarić (submitted). From Jakšetić and Pečarić (submitted), we then also have that s ↦ [y0, y1, y2; g
s
] is exponentially convex.
For this family of functions, μ s, q (x, Φ i , Ξ) (i = 1, 2) from (20) become

Example 4.2. Consider a family of functions

defined by

Here,  which shows that f
s
is convex for x > 0 and
which shows that f
s
is convex for x > 0 and is exponentially convex by Example 1 given in Jakšetić and Pečarić (submitted). From Jakšetić and Pečarić (submitted), we have that s ↦ [y0, y1, y2; f
s
] is exponentially convex.
is exponentially convex by Example 1 given in Jakšetić and Pečarić (submitted). From Jakšetić and Pečarić (submitted), we have that s ↦ [y0, y1, y2; f
s
] is exponentially convex.
In this case, μ s, q (x, Φ i , Ξ) (i = 1, 2) defined in (20) for x j > 0 (j = 1, ..., n) are

If Φ
i
is positive, then Theorem 2.5 applied for f = f
s
∈ Ω2and g = f
q
∈ Ω2yields that there exists  such that
such that

Since the function ξ ↦ ξs-q is invertible for s ≠ q, we then have

which together with the fact that μ s, q (x, Φ i , Ω2) is continuous, symmetric and monotonous (by (23)), shows that μ s, q (x, Φ i , Ω2) is a mean.
Now, by substitutions ,
,  ,
, from (24) we get
from (24) we get

where .
.
We define a new mean (for i = 1, 2) as follows:

These new means are also monotonous. More precisely, for s, q, u, v ∈ ℝ such that s ≤ u, q ≤ v, s ≠ u, q ≠ v, we have

We know that

for s, q, u, v ∈ I such that s/t ≤ u/t, q/t ≤ v/t and t ≠ 0, since μ s, q (x, Φ i , Ω2) are monotonous in both parameters, so the claim follows. For t = 0, we obtain the required result by taking the limit t → 0.
Example 4.3. Consider a family of functions

defined by

Exponential convexity of on (0,∞) is given by Example 2 in Jakšetić and Pečarić (submitted).
on (0,∞) is given by Example 2 in Jakšetić and Pečarić (submitted).
μ s, q (x, Φ i , Ξ) (i = 1, 2) defined in (20) in this case for x j > 0 (j = 1, ..., n) are

Example 4.4. Consider a family of functions

defined by

Exponential convexity of on (0, ∞) is given by Example 3 in Jakšetić and Pečarić (submitted).
on (0, ∞) is given by Example 3 in Jakšetić and Pečarić (submitted).
In this case, μ s, q (x, Φ i , Ξ) (i = 1, 2) defined in (20) for x j > 0 (j = 1, ..., n) are

References
Pečarić JE, Proschan F, Tong YL: Convex Functions, Partial Orderings, and Statistical Applications. Academic Press Inc; 1992.
Steffensen JF: On certain inequalities and methods of approximation. J Inst Actuaries 1919, 51: 274–297.
Vasić PM, Pečarić JE: Sur une inegalite de Jensen-Steffensen. General Inequalities, Birkhauser Verlag, Basel 1984, 4: 87–92.
Khan KA, Pečarić J, Perić I: Differences of weighted mixed symmetric means and related results. J Inequal Appl 2010, 16: 289730.
Mitrinović DS, Pečarić J, Fink AM: Classical and New Inequalities in Analysis. Kluwer, Dordrecht; 1993.
Anwar M, Jakšetić J, Pečarić J, Rehman A: Exponential convexity, positive semi-definite matrices and fundamental inequalities. J Math Inequal 2010,4(2):171–189.
Acknowledgements
This research work was partially funded by Higher Education Commission, Pakistan. The research of the first and the third author was supported by the Croatian Ministry of Science, Education and Sports, under the Research Grants 058-1170889-1050 (Iva Franjić) and 117-1170889-0888 (Josip Pečarić).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
JP made the main contribution in conceiving the presented research. IF and JP worked on the results from Section 2, while SK and JP worked jointly on the results of Sections 3 and 4. IF and SK drafted the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Franjić, I., Khalid, S. & Pečarić, J. On the refinements of the Jensen-Steffensen inequality. J Inequal Appl 2011, 12 (2011). https://doi.org/10.1186/1029-242X-2011-12
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-12