- Research
- Open access
- Published:
A new nonlinear impulsive delay differential inequality and its applications
Journal of Inequalities and Applications volume 2011, Article number: 11 (2011)
Abstract
In this article, a new nonlinear impulsive delay differential inequality is established, which can be applied in the dynamical analysis of nonlinear systems to improve many extant results. Using the inequality, we obtain some sufficient conditions to guarantee the exponential stability of nonlinear impulsive functional differential equations. Two examples are given to illustrate the effectiveness and advantages of our results.
1. Introduction
It is well known that the theory of differential inequalities plays an important role in the qualitative and quantitative studies of differential equations [1–3]. In recent years, various inequalities have been established such as the Halanay inequalities in [4–6], the delay inequalities in [7–10], and the impulsive differential inequalities in [11–13]. Using the linear inequality techniques, many results have been done on the stability and dynamical behavior for differential systems, see [4–13] and the references cited therein. For example, [11] presents an extended impulsive delay Halanay inequality and deals with the global exponential stability of impulsive Hopfield neural networks with time delays. In [13], the authors establish a delay differential inequality with impulsive initial conditions and derive some sufficient conditions ensuring the exponential stability of solutions for the impulsive differential equations. However, linear differential inequalities do not work in the studies for nonlinear differential equations. With the development of the theory on nonlinear differential equations (e.g., see [14, 15]), it is necessary to study the corresponding nonlinear differential inequalities. In [16], the authors develop a new nonlinear delay differential inequality that works well in studying a class of nonlinear delay differential systems. Indeed, nonlinear delay differential inequalities with impulses are seldom discussed in the literature. Therefore, in further researches of nonlinear systems, it is beneficial to obtain some new nonlinear impulsive delay differential inequalities. Our goal in this article is to do some investigations on such problems.
Indeed, impulsive effects and delay effects widely exist in the real world. Impulsive delay differential equations provide mathematical models for many phenomena and processes in the field of natural science and technology. In the last few decades, the stability theory of impulsive functional differential equations has obtained a rapid development, and many interesting results have been reported, see [1–8, 16–23]. Recently, exponential stability has attracted increasing interest in both theoretical research and applications [20–22, 24]. However, the existing works mainly focus on linear impulsive functional differential equations [17–19, 25]. There exist very little works devoted to the investigations of exponential stabilities for nonlinear impulsive functional differential systems.
Motivated by the above discussions, in this article, we shall establish a new nonlinear impulsive delay differential inequality, which improves some recent works in the literature [9–12, 16, 18] and can be applied to the dynamical analysis of nonlinear systems. Based on the inequality, some sufficient conditions guaranteeing the local exponential stability of nonlinear impulsive functional differential equations are derived. Finally, two examples are given to show the effectiveness and advantages of our proposed results.
2. Preliminaries
Let ℝ denote the set of real numbers, ℝ+ the set of nonnegative real numbers, ℤ+ the set of positive integers, and ℝ n the n-dimensional real space equipped with the Euclidean norm | · |. Consider the following impulsive functional differential systems

where x ∈ ℝ n , the impulse times {t
k
} satisfy 0 ≤ t0 < t1 < ⋯ < t
k
< ⋯ and limk→+∞t
k
= +∞, and x' denotes the right-hand derivative of x. Also, assume f ∈ C([tk-1, t
k
) × Ψ, ℝ n ), meanwhile φ ∈ Ψ, Ψ is an open set in PC([-τ, 0], ℝ n ), where PC([-τ, 0], ℝ n ) = {ψ: [-τ, 0] → ℝ n |ψ is continuous except at a finite number of points t
k
, at which  and
and  exist and
exist and  }. For ψ ∈ Ψ , the norm of ψ is defined by ||ψ|| = sup-τ≤θ≤0|ψ(θ)|. For each t ≥ t0, x
t
∈ Ψ is defined by x
t
(s) = x(t + s), s ∈ [-τ, 0]. For each k ∈ ℤ+, I
k
(t,x) ∈ C(t0, ∞) × ℝ n , ℝ n ).
}. For ψ ∈ Ψ , the norm of ψ is defined by ||ψ|| = sup-τ≤θ≤0|ψ(θ)|. For each t ≥ t0, x
t
∈ Ψ is defined by x
t
(s) = x(t + s), s ∈ [-τ, 0]. For each k ∈ ℤ+, I
k
(t,x) ∈ C(t0, ∞) × ℝ n , ℝ n ).
In this article, we suppose that there exists a unique solution of system (2.1) through each (t0, φ), see [23] for the details. Furthermore, we assume that f(t, 0) = 0, and I k (t, 0) = 0, k ∈ ℤ+, so that x(t) = 0 is a solution of system (2.1), which is called the trivial solution.
We now introduce some definitions that will be used in the sequel.
Definition 2.1. ([5]) A function V: [-τ, ∞) × Ψ → ℝ+ belongs to class v0 if
-
(i)
V is continuous on each set [t k - 1, t k ) × Ψ and
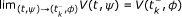 exists,
exists, -
(ii)
V (t, x) is locally Lipschitzian in x and V (t, 0) ≡ 0.
Definition 2.2. ([5]) Let V ∈ v0, for any (t, ψ) ∈ [tk - 1, t k ) × Ψ, the upper right-hand Dini derivative of V (t, x) along a solution of system (2.1) is defined by

Definition 2.3. ([6]) The trivial solution of system (2.1) is said to be exponentially stable, if for any initial data  , there exists a λ > 0, and for every ε > 0, there exists δ = δ(ε) > 0 such that
, there exists a λ > 0, and for every ε > 0, there exists δ = δ(ε) > 0 such that

whenever || φ || < δ and t0 ∈ ℝ+.
Definition 2.4. ([5]) Let x(t) = x(t, t0, φ) be a solution of system (2.1) through (t0, φ). Then the trivial solution of (2.1) is said to be globally exponentially stable if for any t0 > 0, there exist constants λ > 0 and M ≥ 1 such that

3. Main results
First, we present a nonlinear impulsive delay differential inequality.
Lemma 3.1. Assume that there exist constants p > 0, q > 0, θ > 1, and function m(t) ∈ PC([t0 - τ, ∞), ℝ+) satisfying the scalar impulsive differential inequality

where a
k
, b
k
∈ ℝ+,  . Moreover, there exists a constant M ≥ 1 such that
. Moreover, there exists a constant M ≥ 1 such that . Then
. Then implies
implies

where λ satisfies

Proof. We first note that  implies that there exists a scalar λ > 0 such that the inequality (3.2) holds.
implies that there exists a scalar λ > 0 such that the inequality (3.2) holds.
Now, we shall show

where a0 = 1, b0 = 0.
In order to do this, let

Now we only need to show that

It is clear that  for t ∈ [t0 - τ, t0] by the definition of
for t ∈ [t0 - τ, t0] by the definition of  .
.
Take k = 1, we can prove that  for t ∈ [t0, t1). Suppose on the contrary, then there exists some t ∈ [t0, t1) such that
for t ∈ [t0, t1). Suppose on the contrary, then there exists some t ∈ [t0, t1) such that  .
.
Let  , then
, then  ,
,  , t ∈ [t0 - τ , t*], and D+L(t*) ≥ 0. Calculating the upper right-hand Dini derivative of L(t) along the solution of (2.1), it can be deduced that
, t ∈ [t0 - τ , t*], and D+L(t*) ≥ 0. Calculating the upper right-hand Dini derivative of L(t) along the solution of (2.1), it can be deduced that

which is a contradiction. So we have proven  for all t ∈ [t0, t1).
for all t ∈ [t0, t1).
Furthermore, we have

Next we shall show  . Suppose on the contrary, then there exists some t ∈ [t1, t2) such that
. Suppose on the contrary, then there exists some t ∈ [t1, t2) such that  . Let
. Let  , then
, then  , and
, and  , t ∈ [t0 - τ , t** ], D+L(t**) ≥ 0. Calculating the upper right-hand Dini derivative of L(t) along the solution of (2.1), it can be deduced that
, t ∈ [t0 - τ , t** ], D+L(t**) ≥ 0. Calculating the upper right-hand Dini derivative of L(t) along the solution of (2.1), it can be deduced that

which is a contradiction. So we have proven  for all t ∈ [t1, t2).
for all t ∈ [t1, t2).
By the method of induction, we prove that for t ∈ [t k -1, t k ], k ∈ ℤ+,

i.e.,

So (3.1) holds. The proof of Lemma 3.1 is complete.
Remark 3.1. In [9–18], the authors got some results for linear differential inequalities under the assumption that p > q. Note in our result, the restriction p > q is completely removed if the initial value satisfies some certain conditions.
Remark 3.2. It should be noted that if p > q, then  , which implies that (3.1) holds for any initial value
, which implies that (3.1) holds for any initial value  . In this sense, Lemma 3.1 becomes the well known case, see [16]. Hence, our development result has wider adaptive range than those in [9–12, 16, 18].
. In this sense, Lemma 3.1 becomes the well known case, see [16]. Hence, our development result has wider adaptive range than those in [9–12, 16, 18].
Next, based on Lemma 3.1, we shall construct a suitable Lyapunov function to derive some conditions guaranteeing the exponential stability of the trivial solution of system (2.1).
Theorem 3.1. Assume that there exist function V (t, x) ∈ v0, and constants 0 < c1 ≤ c2, m > 0, p > 0, q > 0, θ > 1 such that the following conditions hold:
-
(i)
c 1||x|| m ≤ V (t, x) ≤ c 2||x|| m , (t, x) ∈ (ℝ+,ℝ n );
-
(ii)
For t ≥ t 0, t ≠ t k ,
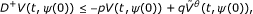
where ;
;
-
(iii)
For any ψ ∈ PC([ - τ , 0], Rn ),
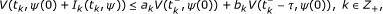
where .
.
Then the trivial solution of system (2.1) is exponentially stable.
Proof. Let x(t) = x(t, t0, φ) be any solution of system (2.1) with initial value (t0, φ). By condition (iii), we know that there exists M ≥ 1 such that  .
.
For any given  , choose some δ > 0 such that
, choose some δ > 0 such that  . When ||φ|| < δ < ε, we have
. When ||φ|| < δ < ε, we have  . Using Lemma 3.1 and the condition (i), we derive
. Using Lemma 3.1 and the condition (i), we derive

i.e.,

By the definition 2.3, the trivial solution of system (2:1) is exponentially stable. This completes the proof.
Remark 3.3. From the proof of the Theorem 3.1, it follows that if p > q, θ → 1+, the trivial solution of system (2.1) is globally exponentially stable.
4. Examples
In this section, we shall give two examples to illustrate the effectiveness of our results.
Example 1. Consider the impulsive functional differential equation as follows:

where θ > 1, a(t) ≥ a > 0, 0 < |b(t)| ≤ b, 0 ≤ τ (t) ≤ τ, for all t ≥ t0.
Property 4.1. The trivial solution of system (4.1) is exponentially stable.
Proof. Choose V (t) = |x(t)|. When t ≠ t k , calculating the derivative of D+V (t) along the solution of (4.1), we get

where  . Furthermore,
. Furthermore,

Hence, by Theorem 3.1, the trivial solution of system (4.1) is exponentially stable.
Example 2. Consider the following impulsive functional differential equation with distributed delays:

where θ > 1, a > 0, b ∈ ℝ.
Property 4.2. The trivial solution of system (4.2) is exponentially stable.
Proof. Choose V (t) = |x(t)|. When t ≠ t k , calculating the derivative of D+V (t) along the solution of (4:2), we get

where  . Furthermore, we have
. Furthermore, we have

Hence, by Theorm 3.1, the trivial solution of system (4.2) is exponentially stable.
Remark 3.4 It should be noted that the sufficient conditions ensuring the exponential stabilities of (4.1) and (4.2) are easily to check, which show the advantages of our results.
References
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. World Scientific, Singapore 1989.
Lakshmikantham V, Leela S: Differential and Integral Inequalities. Academic Press, New York; 1969.
Bainov DD, Simenov PS: Systems with Impulse Effect: Stability Theory and Applications. Ellis Horwood Limited, Chichester; 1989.
Halanay A: Differential Equations, Stability, Oscillation, Time Lags. Academic Press, New York; 1996.
Baker CTH, Tang A: Generalized Halanay inequalities for Volterra functional differential equations and discretised versions. In Volterra Equations and Applications. Edited by: Corduneanu C, Sandberg IW. Gordon and Breach, Amsterdam; 1999.
Gopalsamy K: Stability and Oscillations in Delay Differential Equations of Population Dynamics. Kluwer Academic, Dordrecht; 1992.
Tian H: The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag. J Math Anal Appl 2002,270(1):143–149. 10.1016/S0022-247X(02)00056-2
Jiang M, Shen Y, Liao X: On the global exponential stability for functional differential equations. Commun Nonlinear Sci Numer Simul 2005,10(7):705–713. 10.1016/j.cnsns.2004.05.002
Nieto J: Differential inequalities for functional perturbations of first-order ordinary differential equations. Appl Math Lett 2002,15(2):173–179. 10.1016/S0893-9659(01)00114-8
Ladas G, Stavroulakis P: On delay differential inequalities of first order. Funkcialaj Ekvacioj 1982,25(1):105–113.
Fu X, Li X: Global exponential stability and global attractivity of impulsive Hopfield nenural networks with time delays. J Comput Appl Math 2009,231(1):187–199. 10.1016/j.cam.2009.02.094
Li X: Existence and global exponential stability of periodic solution for impulsive Cohen-Grossberg-type BAM neural networks with continuously distributed delays. Appl Math Comput 2009,215(1):292–307. 10.1016/j.amc.2009.05.005
Xu D, Yang Z: Impulsive delay differential inequality and stability of neural networks. J Math Anal Appl 2005,305(1):107–120. 10.1016/j.jmaa.2004.10.040
El-Gebeily MA, O'Regan D: Existence and boundary behavior for singular nonlinear differential equations with arbitrary boundary conditions. J Math Anal Appl 2007,334(1):140–156. 10.1016/j.jmaa.2006.12.040
O'Regan D, El-Gebeily MA: Existence, upper and lower solutions and quasilinearization for singular differential equations. IMA J Appl Math 2008,73(1):323–344.
Xu D, Xu L: New results for studying a certain class nonlinear delay differential systems. IEEE Trans Autom Control 2010,55(7):1641–1645.
Fu X, Li X: Razumikhin-type theorems on exponential stability of impulsive infinite delay differential systems. J Comput Appl Math 2009,224(1):1–10. 10.1016/j.cam.2008.03.042
Wang Q, Liu X: Exponential stability for impulsive delay differential equations by Razumikhin method. J Math Anal Appl 2005,309(2):462–473. 10.1016/j.jmaa.2004.09.016
Wang Q, Liu X: Impulsive stabilization of delay differential systems via the Lyapunov-Razumikhin method. Appl Math Lett 2007,20(8):839–845. 10.1016/j.aml.2006.08.016
Anokhin A, Berezansky L, Braverman E: Exponential stability of linear delay impulsive differential equations. J Math Anal Appl 1995,193(3):923–941. 10.1006/jmaa.1995.1275
Berezansky L, Idels L: Exponential stability of some scalar impulsive delay differential equation. Commun Appl Math Anal 1998,2(1):301–309.
Li X: New results on global exponential stabilization of impulsive functional differential equations with infinite delays or finite delays. Nonlinear Anal Real World Appl 2010,11(5):4194–4201. 10.1016/j.nonrwa.2010.05.006
Ballinger G, Liu X: Existence and uniqueness results for impulsive delay differential equations. Dyn Continuous Discr Impulsive Syst 1999,5(1):579–591.
Li X: Uniform asymptotic stability and global stability of impulsive infinite delay differential equations. Nonlinear Anal Theory Methods Appl 2009,70(5):1975–1983. 10.1016/j.na.2008.02.096
Stamova IM, Stamov GT: Lyapunov-Razumikhin method for impulsive functional differential equations and applications to the population dynamics. J Comput Appl Math 2001,130(1–2):163–171. 10.1016/S0377-0427(99)00385-4
Acknowledgements
The authors sincerely thanks the referees for their valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
HW designed and performed all the steps of proof in this research and also wrote the paper. CD participated in the design of the study and suggest many good ideas that made this paper possible and helped to draft the first manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, H., Ding, C. A new nonlinear impulsive delay differential inequality and its applications. J Inequal Appl 2011, 11 (2011). https://doi.org/10.1186/1029-242X-2011-11
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-11
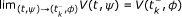 exists,
exists,