- Research Article
- Open access
- Published:
Periodic solutions of second-order Liénard equations with -Laplacian-like operators
-Laplacian-like operators
Journal of Inequalities and Applications volume 2006, Article number: 98685 (2006)
Abstract
The existence of periodic solutions for second-order Liénard equations with -Laplacian-like operator is studied by applying new generalization of polar coordinates.
-Laplacian-like operator is studied by applying new generalization of polar coordinates.
References
Burton TA, Townsend CG: On the generalized Liénard equation with forcing function. Journal of Differential Equations 1968,4(4):620–633. 10.1016/0022-0396(68)90012-0
del Pino MA, Manásevich RF, Murúa AE: Existence and multiplicity of solutions with prescribed period for a second order quasilinear ODE. Nonlinear Analysis. Theory, Methods & Applications 1992,18(1):79–92. 10.1016/0362-546X(92)90048-J
del Pino MA, Manásevich RF, Murúa A: On the number of
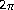 periodic solutions for
periodic solutions for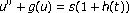 using the Poincaré-Birkhoff theorem. Journal of Differential Equations 1992,95(2):240–258. 10.1016/0022-0396(92)90031-H
using the Poincaré-Birkhoff theorem. Journal of Differential Equations 1992,95(2):240–258. 10.1016/0022-0396(92)90031-HDing TR, Iannacci R, Zanolin F: Existence and multiplicity results for periodic solutions of semilinear Duffing equations. Journal of Differential Equations 1993,105(2):364–409. 10.1006/jdeq.1993.1093
Fabry C, Fayyad D: Periodic solutions of second order differential equations with a
 -Laplacian and asymmetric nonlinearities. Rendiconti dell'Istituto di Matematica dell'Università di Trieste 1992,24(1–2):207–227 (1994).
-Laplacian and asymmetric nonlinearities. Rendiconti dell'Istituto di Matematica dell'Università di Trieste 1992,24(1–2):207–227 (1994).Fabry C, Mawhin J, Nkashama MN: A multiplicity result for periodic solutions of forced nonlinear second order ordinary differential equations. Bulletin of the London Mathematical Society 1986,18(2):173–180. 10.1112/blms/18.2.173
Gossez J-P, Omari P: Periodic solutions of a second order ordinary differential equation: a necessary and sufficient condition for nonresonance. Journal of Differential Equations 1991,94(1):67–82. 10.1016/0022-0396(91)90103-G
Manásevich RF, Mawhin J: Periodic solutions for nonlinear systems with
 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367–393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367–393. 10.1006/jdeq.1998.3425Mawhin J, Ward JR Jr.: Periodic solutions of some forced Liénard differential equations at resonance. Archiv der Mathematik 1983,41(4):337–351. 10.1007/BF01371406
Omari P, Villari G, Zanolin F: Periodic solutions of the Liénard equation with one-sided growth restrictions. Journal of Differential Equations 1987,67(2):278–293. 10.1016/0022-0396(87)90151-3
Sandqvist A, Andersen KM: A necessary and sufficient condition for the existence of a unique nontrivial periodic solution to a class of equations of Liénard's type. Journal of Differential Equations 1982,46(3):356–378. 10.1016/0022-0396(82)90100-0
Savel'ev PN: Dissipativity of the generalized Liénard equation. Differential Equations 1992,28(6):794–800.
Sun W, Ge W: The existence of solutions to Sturm-Liouville boundary value problems with Laplacian-like operator. Acta Mathematicae Applicatae Sinica 2002,18(2):341–348. 10.1007/s102550200034
Villari G: On the existence of periodic solutions for Liénard's equation. Nonlinear Analysis 1983,7(1):71–78. 10.1016/0362-546X(83)90104-9
Wang Z: Periodic solutions of the second-order forced Liénard equation via time maps. Nonlinear Analysis. Theory, Methods & Applications. Ser. A: Theory Methods 2002,48(3):445–460.
Wang Y, Ge W: Existence of periodic solutions for nonlinear differential equations with a-Laplacian-like operator. to appear in Applied Mathematics Letters to appear in Applied Mathematics Letters
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Y., Ge, W. Periodic solutions of second-order Liénard equations with -Laplacian-like operators.
J Inequal Appl 2006, 98685 (2006). https://doi.org/10.1155/JIA/2006/98685
-Laplacian-like operators.
J Inequal Appl 2006, 98685 (2006). https://doi.org/10.1155/JIA/2006/98685
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/98685
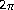 periodic solutions for
periodic solutions for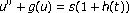 using the Poincaré-Birkhoff theorem. Journal of Differential Equations 1992,95(2):240–258. 10.1016/0022-0396(92)90031-H
using the Poincaré-Birkhoff theorem. Journal of Differential Equations 1992,95(2):240–258. 10.1016/0022-0396(92)90031-H -Laplacian and asymmetric nonlinearities. Rendiconti dell'Istituto di Matematica dell'Università di Trieste 1992,24(1–2):207–227 (1994).
-Laplacian and asymmetric nonlinearities. Rendiconti dell'Istituto di Matematica dell'Università di Trieste 1992,24(1–2):207–227 (1994). -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367–393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367–393. 10.1006/jdeq.1998.3425