- Research Article
- Open access
- Published:
On the boundedness of maximal operators and singular operators with kernels in
Journal of Inequalities and Applications volume 2006, Article number: 96732 (2006)
Abstract
We establish the -boundedness for a class of singular integral operators and a class of related maximal operators when their singular kernels are given by functions
-boundedness for a class of singular integral operators and a class of related maximal operators when their singular kernels are given by functions in
in .
.
References
Al-Qassem HM: bounds for a class of rough maximal operators. preprint preprint
Al-Qassem HM, Pan Y:
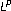 estimates for singular integrals with kernels belonging to certain block spaces. Revista Matemática Iberoamericana 2002,18(3):701–730.
estimates for singular integrals with kernels belonging to certain block spaces. Revista Matemática Iberoamericana 2002,18(3):701–730.Al-Qassem HM, Pan Y: Singular integrals along surfaces of revolution with rough kernels. SUT Journal of Mathematics 2003,39(1):55–70.
Al-Salman A, Pan Y: Singular integrals with rough kernels in
 . Journal of the London Mathematical Society. Second Series 2002,66(1):153–174. 10.1112/S0024610702003241
. Journal of the London Mathematical Society. Second Series 2002,66(1):153–174. 10.1112/S0024610702003241Ash JM, Ash PF, Fefferman CL, Jones RL: Singular integral operators with complex homogeneity. Studia Mathematica 1979,65(1):31–50.
Benedek A, Panzone R: The space
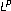 , with mixed norm. Duke Mathematical Journal 1961,28(3):301–324. 10.1215/S0012-7094-61-02828-9
, with mixed norm. Duke Mathematical Journal 1961,28(3):301–324. 10.1215/S0012-7094-61-02828-9Calderón AP, Zygmund A: On the existence of certain singular integrals. Acta Mathematica 1952,88(1):85–139. 10.1007/BF02392130
Calderón AP, Zygmund A: On singular integrals. American Journal of Mathematics 1956, 78: 289–309. 10.2307/2372517
Chen L-K: On a singular integral. Studia Mathematica 1986,85(1):61–72, 1987.
Chen L-K, Lin H: A maximal operator related to a class of singular integrals. Illinois Journal of Mathematics 1990,34(1):120–126.
Coifman RR, Weiss G: Extensions of Hardy spaces and their use in analysis. Bulletin of the American Mathematical Society 1977,83(4):569–645. 10.1090/S0002-9904-1977-14325-5
Ding Y, He Q: Weighted boundedness of a rough maximal operator. Acta Mathematica Scientia. English Edition 2000,20(3):417–422.
Duoandikoetxea J, Rubio de Francia JL: Maximal and singular integral operators via Fourier transform estimates. Inventiones Mathematicae 1986,84(3):541–561. 10.1007/BF01388746
Fan D, Pan Y: A singular integral operator with rough kernel. Proceedings of the American Mathematical Society 1997,125(12):3695–3703. 10.1090/S0002-9939-97-04111-7
Fan D, Pan Y: Singular integral operators with rough kernels supported by subvarieties. American Journal of Mathematics 1997,119(4):799–839. 10.1353/ajm.1997.0024
Fan D, Pan Y, Yang D: A weighted norm inequality for rough singular integrals. The Tohoku Mathematical Journal 1999,51(2):141–161. 10.2748/tmj/1178224808
Fefferman R: A note on singular integrals. Proceedings of the American Mathematical Society 1979,74(2):266–270. 10.1090/S0002-9939-1979-0524298-3
Kim W-J, Wainger S, Wright J, Ziesler S: Singular integrals and maximal functions associated to surfaces of revolution. The Bulletin of the London Mathematical Society 1996,28(3):291–296. 10.1112/blms/28.3.291
Le HV: Maximal operators and singular integral operators along submanifolds. Journal of Mathematical Analysis and Applications 2004,296(1):44–64. 10.1016/j.jmaa.2004.02.056
Namazi J: A singular integral. Proceedings of the American Mathematical Society 1986,96(3):421–424. 10.1090/S0002-9939-1986-0822432-2
Stein EM: Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, no. 30. Princeton University Press, New Jersey; 1970:xiv+290.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Al-Qassem, H.M. On the boundedness of maximal operators and singular operators with kernels in .
J Inequal Appl 2006, 96732 (2006). https://doi.org/10.1155/JIA/2006/96732
.
J Inequal Appl 2006, 96732 (2006). https://doi.org/10.1155/JIA/2006/96732
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/96732
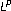 estimates for singular integrals with kernels belonging to certain block spaces. Revista Matemática Iberoamericana 2002,18(3):701–730.
estimates for singular integrals with kernels belonging to certain block spaces. Revista Matemática Iberoamericana 2002,18(3):701–730. . Journal of the London Mathematical Society. Second Series 2002,66(1):153–174. 10.1112/S0024610702003241
. Journal of the London Mathematical Society. Second Series 2002,66(1):153–174. 10.1112/S0024610702003241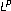 , with mixed norm. Duke Mathematical Journal 1961,28(3):301–324. 10.1215/S0012-7094-61-02828-9
, with mixed norm. Duke Mathematical Journal 1961,28(3):301–324. 10.1215/S0012-7094-61-02828-9