- Research Article
- Open access
- Published:
Strong convergence bounds of the Hill-type estimator under second-order regularly varying conditions
Journal of Inequalities and Applications volume 2006, Article number: 95124 (2006)
Abstract
Bounds on strong convergences of the Hill-type estimator are established under second-order regularly varying conditions.
References
De Haan L: Extreme value statistics. In Extreme Value Theory and Applications. Edited by: Galambos J. Kluwer Academic, Massachusetts; 1994:93–122.
Deheuvels P: Strong laws for the
 th order statistic when
th order statistic when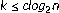 . Probability Theory and Related Fields 1986,72(1):133–154. 10.1007/BF00343900
. Probability Theory and Related Fields 1986,72(1):133–154. 10.1007/BF00343900Deheuvels P: Strong laws for the
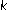 th order statistic when
th order statistic when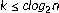 . II. In Extreme Value Theory (Oberwolfach, 1987), Lecture Notes in Statistics. Volume 51. Springer, New York; 1989:21–35.
. II. In Extreme Value Theory (Oberwolfach, 1987), Lecture Notes in Statistics. Volume 51. Springer, New York; 1989:21–35.Deheuvels P, Mason DM: The asymptotic behavior of sums of exponential extreme values. Bulletin des Sciences Mathematiques, Series 2 1988,112(2):211–233.
Dekkers ALM, de Haan L: On the estimation of the extreme-value index and large quantile estimation. The Annals of Statistics 1989,17(4):1795–1832. 10.1214/aos/1176347396
Dekkers ALM, Einmahl JHJ, de Haan L: A moment estimator for the index of an extreme-value distribution. The Annals of Statistics 1989,17(4):1833–1855. 10.1214/aos/1176347397
Drees H: On smooth statistical tail functionals. Scandinavian Journal of Statistics 1998,25(1):187–210. 10.1111/1467-9469.00097
Hill BM: A simple general approach to inference about the tail of a distribution. The Annals of Statistics 1975,3(5):1163–1174. 10.1214/aos/1176343247
Pan J: Rate of strong convergence of Pickands' estimator. Acta Scientiarum Naturalium Universitatis Pekinensis 1995,31(3):291–296.
Peng Z: An extension of a Pickands-type estimator. Acta Mathematica Sinica 1997,40(5):759–762.
Pickands J III: Statistical inference using extreme order statistics. The Annals of Statistics 1975,3(1):119–131. 10.1214/aos/1176343003
Resnick SI: Extreme Values, Regular Variation, and Point Processes, Applied Probability. A Series of the Applied Probability Trust. Volume 4. Springer, New York; 1987:xii+320.
Wellner JA: Limit theorems for the ratio of the empirical distribution function to the true distribution function. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1978,45(1):73–88. 10.1007/BF00635964
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Peng, Z., Nadarajah, S. Strong convergence bounds of the Hill-type estimator under second-order regularly varying conditions. J Inequal Appl 2006, 95124 (2006). https://doi.org/10.1155/JIA/2006/95124
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/95124
 th order statistic when
th order statistic when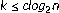 . Probability Theory and Related Fields 1986,72(1):133–154. 10.1007/BF00343900
. Probability Theory and Related Fields 1986,72(1):133–154. 10.1007/BF00343900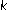 th order statistic when
th order statistic when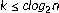 . II. In Extreme Value Theory (Oberwolfach, 1987), Lecture Notes in Statistics. Volume 51. Springer, New York; 1989:21–35.
. II. In Extreme Value Theory (Oberwolfach, 1987), Lecture Notes in Statistics. Volume 51. Springer, New York; 1989:21–35.