- Research Article
- Open access
- Published:
To a nonlocal generalization of the Dirichlet problem
Journal of Inequalities and Applications volume 2006, Article number: 93858 (2006)
Abstract
A mixed problem with a boundary Dirichlet condition and nonlocal integral condition is considered for a two-dimensional elliptic equation.The existence and uniqueness of a weak solution of this problem are proved in a weighted Sobolev space.
References
Cannon JR: The solution of the heat equation subject to the specification of energy. Quarterly of Applied Mathematics 1963,21(2):155–160.
Chipot M, Lovat B: Some remarks on nonlocal elliptic and parabolic problems. Nonlinear Analysis 1997,30(7):4619–4627. 10.1016/S0362-546X(97)00169-7
Ciarlet PG: The Finite Element Method for Elliptic Problems, Studies in Mathematics and Its Applications. Volume 4. North-Holland, Amsterdam; 1978:xix+530.
De Schepper H, Slodička M: Recovery of the boundary data for a linear second order elliptic problem with a nonlocal boundary condition. ANZIAM Journal 2000, 42: Part C, C518-C535.
Gordeziani D, Avalishvili G: Investigation of the nonlocal initial boundary value problems for some hyperbolic equations. Hiroshima Mathematical Journal 2001,31(3):345–366.
Gushchin AK, Mikhaĭlov VP: On the solvability of nonlocal problems for a second-order elliptic equation. Matematicheskiĭ Sbornik 1994,185(1):121–160. translated in Russian Acad. Sci. Sb. Math. 81 (1995), no. 1, 101–136 translated in Russian Acad. Sci. Sb. Math. 81 (1995), no. 1, 101–136
Kufner A, Sändig A-M: Some Applications of Weighted Sobolev Spaces, Teubner-Texte zur Mathematik. Volume 100. BSB B. G. Teubner, Leipzig; 1987:268.
Martynyuk AE: Some new applications of methods of Galerkin type. Matematicheskiĭ Sbornik 1959, 49 (91): 85–108.
Mesloub S, Bouziani A, Kechkar N: A strong solution of an evolution problem with integral conditions. Georgian Mathematical Journal 2002,9(1):149–159.
Nekvinda A, Pick L: A note on the Dirichlet problem for the elliptic linear operator in Sobolev spaces with weight
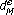 . Commentationes Mathematicae Universitatis Carolinae 1988,29(1):63–71.
. Commentationes Mathematicae Universitatis Carolinae 1988,29(1):63–71.Paneyakh BP: Some nonlocal boundary value problems for linear differential operators. Matematicheskie Zametki 1984,35(3):425–434.
Petryshyn WV: On a class of
 and non
and non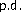 operators and operator equations. Journal of Mathematical Analysis and Applications 1965,10(1):1–24. 10.1016/0022-247X(65)90142-3
operators and operator equations. Journal of Mathematical Analysis and Applications 1965,10(1):1–24. 10.1016/0022-247X(65)90142-3Sapagovas MP: A difference scheme for two-dimensional elliptic problems with an integral condition. Litovsk. Mat. Sb. 1983,23(3):155–159.
Skubachevskiĭ AL, Steblov GM: On the spectrum of differential operators with a domain that is not dense in. Doklady Akademii Nauk SSSR 1991,321(6):1158–1163. translated in Soviet Mathematics Doklady 44 (1992), no. 3, 870–875 translated in Soviet Mathematics Doklady 44 (1992), no. 3, 870–875
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Berikelashvili, G. To a nonlocal generalization of the Dirichlet problem. J Inequal Appl 2006, 93858 (2006). https://doi.org/10.1155/JIA/2006/93858
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/93858
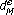 . Commentationes Mathematicae Universitatis Carolinae 1988,29(1):63–71.
. Commentationes Mathematicae Universitatis Carolinae 1988,29(1):63–71. and non
and non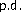 operators and operator equations. Journal of Mathematical Analysis and Applications 1965,10(1):1–24. 10.1016/0022-247X(65)90142-3
operators and operator equations. Journal of Mathematical Analysis and Applications 1965,10(1):1–24. 10.1016/0022-247X(65)90142-3