- Research Article
- Open access
- Published:
Boundary behaviour of analytic functions in spaces of Dirichlet type
Journal of Inequalities and Applications volume 2006, Article number: 927957 (2006)
Abstract
For and
and , we let
, we let be the space of all analytic functions
be the space of all analytic functions in
in such that
such that belongs to the weighted Bergman space
belongs to the weighted Bergman space . We obtain a number of sharp results concerning the existence of tangential limits for functions in the spaces
. We obtain a number of sharp results concerning the existence of tangential limits for functions in the spaces . We also study the size of the exceptional set
. We also study the size of the exceptional set , where
, where denotes the radial variation of
denotes the radial variation of along the radius
along the radius , for functions
, for functions .
.
References
Ahern PR: The mean modulus and the derivative of an inner function. Indiana University Mathematics Journal 1979,28(2):311–347. 10.1512/iumj.1979.28.28022
Ahern PR, Clark DN: On inner functions with
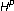 -derivative. The Michigan Mathematical Journal 1974, 21: 115–127.
-derivative. The Michigan Mathematical Journal 1974, 21: 115–127.Arazy J, Fisher SD, Peetre J: Möbius invariant function spaces. Journal für die reine und angewandte Mathematik 1985, 363: 110–145.
Baernstein A II, Girela D, Peláez JÁ: Univalent functions, Hardy spaces and spaces of Dirichlet type. Illinois Journal of Mathematics 2004,48(3):837–859.
Beurling A: Ensembles exceptionnels. Acta Mathematica 1939, 72: 1–13.
Buckley SM, Koskela P, Vukotić D: Fractional integration, differentiation, and weighted Bergman spaces. Mathematical Proceedings of the Cambridge Philosophical Society 1999,126(2):369–385. 10.1017/S030500419800334X
Cargo GT: Angular and tangential limits of Blaschke products and their successive derivatives. Canadian Journal of Mathematics 1962, 14: 334–348. 10.4153/CJM-1962-026-2
Collingwood EF, Lohwater AJ: The Theory of Cluster Sets, Cambridge Tracts in Mathematics and Mathematical Physics, no. 56. Cambridge University Press, Cambridge; 1966:xi+211.
Donaire JJ, Girela D, Vukotić D: On univalent functions in some Möbius invariant spaces. Journal für die reine und angewandte Mathematik 2002, 553: 43–72.
Duren PL: Theory of Hp Spaces, Pure and Applied Mathematics. Volume 38. Academic Press, New York; 1970:xii+258. reprint: Dover, New York, 2000
Duren PL, Schuster AP: Bergman Spaces, Mathematical Surveys and Monographs. Volume 100. American Mathematical Society, Rhode Island; 2004:x+318.
Flett TM: The dual of an inequality of Hardy and Littlewood and some related inequalities. Journal of Mathematical Analysis and Applications 1972, 38: 746–765. 10.1016/0022-247X(72)90081-9
Girela D, Peláez JÁ: Non-stable classes of analytic functions. International Journal of Pure and Applied Mathematics 2005,21(4):553–563.
Girela D, Peláez JÁ: Carleson measures for spaces of Dirichlet type. to appear in Integral Equations and Operator Theory to appear in Integral Equations and Operator Theory
Girela D, Peláez JÁ: Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type. to appear in Journal of the Australian Mathematical Society to appear in Journal of the Australian Mathematical Society
Hedenmalm H, Korenblum B, Zhu KH: Theory of Bergman Spaces, Graduate Texts in Mathematics. Volume 199. Springer, New York; 2000:x+286.
Kahane J-P, Salem R: Ensembles parfaits et séries trigonométriques, Actualités Sci. Indust., no. 1301. Hermann, Paris; 1963:192.
Kim HO: Derivatives of Blaschke products. Pacific Journal of Mathematics 1984,114(1):175–190.
Kinney JR: Tangential limits of functions of the class
 . Proceedings of the American Mathematical Society 1963, 14: 68–70.
. Proceedings of the American Mathematical Society 1963, 14: 68–70.Littlewood JE: On a theorem of Fatou. Journal of the London Mathematical Society 1927, 2: 172–176. 10.1112/jlms/s1-2.3.172
Littlewood JE, Paley REAC: Theorems on Fourier series and power series. II. Proceedings of the London Mathematical Society 1936, 42: 52–89.
Lohwater AJ, Piranian G: The boundary behavior of functions analytic in a disk. Annales Academiae Scientiarum Fennicae. Series A I 1957,1957(239):17.
Nagel A, Rudin W, Shapiro JH: Tangential boundary behavior of functions in Dirichlet-type spaces. Annals of Mathematics. Second Series 1982,116(2):331–360. 10.2307/2007064
Protas D: Blaschke products with derivative in
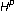 and
and 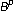 . The Michigan Mathematical Journal 1973, 20: 393–396.
. The Michigan Mathematical Journal 1973, 20: 393–396.Rudin W: The radial variation of analytic functions. Duke Mathematical Journal 1955,22(2):235–242. 10.1215/S0012-7094-55-02224-9
Twomey JB: Tangential limits for certain classes of analytic functions. Mathematika 1989,36(1):39–49. 10.1112/S0025579300013553
Twomey JB: Radial variation of functions in Dirichlet-type spaces. Mathematika 1997,44(2):267–277. 10.1112/S0025579300012596
Vinogradov SA: Multiplication and division in the space of analytic functions with an area-integrable derivative, and in some related spaces. Rossiĭ skaya Akademiya Nauk. Sankt-Peterburgskoe Otdelenie. Matematicheskiĭ Institut im. V. A. Steklova. Zapiski Nauchnykh Seminarov (POMI) 1995,222(23):45–77, 308. translation in Journal of Mathematical Sciences (New York) 87 (1997), no. 5, 3806–3827, Issled. po Linein. Oper. i Teor. Funktsii translation in Journal of Mathematical Sciences (New York) 87 (1997), no. 5, 3806–3827, Issled. po Linein. Oper. i Teor. Funktsii
Zhu KH: Analytic Besov spaces. Journal of Mathematical Analysis and Applications 1991,157(2):318–336. 10.1016/0022-247X(91)90091-D
Zygmund A: On certain integrals. Transactions of the American Mathematical Society 1944,55(2):170–204. 10.2307/1990189
Zygmund A: On a theorem of Littlewood. Summa Brasiliensis Mathematicae 1949,2(5):51–57.
Zygmund A: Trigonometric Series. Vols. I, II. 2nd edition. Cambridge University Press, New York; 1959:xii+383, vii+354.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Girela, D., Peláez, J.Á. Boundary behaviour of analytic functions in spaces of Dirichlet type. J Inequal Appl 2006, 927957 (2006). https://doi.org/10.1155/JIA/2006/92795
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/92795
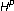 -derivative. The Michigan Mathematical Journal 1974, 21: 115–127.
-derivative. The Michigan Mathematical Journal 1974, 21: 115–127. . Proceedings of the American Mathematical Society 1963, 14: 68–70.
. Proceedings of the American Mathematical Society 1963, 14: 68–70.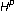 and
and 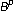 . The Michigan Mathematical Journal 1973, 20: 393–396.
. The Michigan Mathematical Journal 1973, 20: 393–396.