- Research Article
- Open access
- Published:
Limiting case of the boundedness of fractional integral operators on nonhomogeneous space
Journal of Inequalities and Applications volume 2006, Article number: 092470 (2006)
Abstract
We show the boundedness of fractional integral operators by means of extrapolation. We also show that our result is sharp.
References
Edmunds DE, Kokilashvili V, Meskhi A: Bounded and Compact Integral Operators, Mathematics and Its Applications. Volume 543. Kluwer Academic, Dordrecht; 2002:xvi+643. chapter 6 chapter 6
García-Cuerva J, Gatto AE: Boundedness properties of fractional integral operators associated to non-doubling measures. Studia Mathematica 2004,162(3):245–261. 10.4064/sm162-3-5
Han Y, Yang D: Triebel-Lizorkin spaces with non-doubling measures. Studia Mathematica 2004,162(2):105–140. 10.4064/sm162-2-2
Kokilashvili V: Weighted estimates for classical integral operators. In Nonlinear Analysis, Function Spaces and Applications, Vol. 4 (Roudnice nad Labem, 1990), Teubner-Texte Math.. Volume 119. Teubner, Leipzig; 1990:86–103.
Kokilashvili V, Meskhi A: Fractional integrals on measure spaces. Fractional Calculus & Applied Analysis 2001,4(1):1–24.
Nakai E: Generalized fractional integrals on Orlicz-Morrey spaces. In Banach and Function Spaces. Yokohama Publishers, Yokohama; 2004:323–333.
Nazarov F, Treil S, Volberg A: Weak type estimates and Cotlar inequalities for Calderón-Zygmund operators on nonhomogeneous spaces. International Mathematics Research Notices 1998,1998(9):463–487. 10.1155/S1073792898000312
Nazarov F, Treil S, Volberg A: The
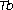 -theorem on non-homogeneous spaces. Acta Mathematica 2003,190(2):151–239. 10.1007/BF02392690
-theorem on non-homogeneous spaces. Acta Mathematica 2003,190(2):151–239. 10.1007/BF02392690Sawano Y:
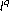 -valued extension of the fractional maximal operators for non-doubling measures via potential operators. International Journal of Pure and Applied Mathematics 2006,26(4):505–523.
-valued extension of the fractional maximal operators for non-doubling measures via potential operators. International Journal of Pure and Applied Mathematics 2006,26(4):505–523.Sawano Y, Tanaka H: Morrey spaces for non-doubling measures. Acta Mathematica Sinica 2005,21(6):1535–1544. 10.1007/s10114-005-0660-z
Tolsa X: BMO,
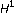 , and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432
, and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432Tolsa X: Painlevé's problem and the semiadditivity of analytic capacity. Acta Mathematica 2003,190(1):105–149. 10.1007/BF02393237
Tolsa X: Bilipschitz maps, analytic capacity, and the Cauchy integral. Annals of Mathematics 2005,162(3):1243–1304. 10.4007/annals.2005.162.1243
Trudinger NS: On imbeddings into Orlicz spaces and some applications. Journal of Mathematics and Mechanics 1967, 17: 473–483.
Zygmund A: Trigonometric Series. Vols. I, II. 2nd edition. Cambridge University Press, New York; 1959:Vol. I. xii+383; Vol. II. vii+354.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sawano, Y., Sobukawa, T. & Tanaka, H. Limiting case of the boundedness of fractional integral operators on nonhomogeneous space. J Inequal Appl 2006, 092470 (2006). https://doi.org/10.1155/JIA/2006/92470
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/92470
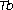 -theorem on non-homogeneous spaces. Acta Mathematica 2003,190(2):151–239. 10.1007/BF02392690
-theorem on non-homogeneous spaces. Acta Mathematica 2003,190(2):151–239. 10.1007/BF02392690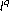 -valued extension of the fractional maximal operators for non-doubling measures via potential operators. International Journal of Pure and Applied Mathematics 2006,26(4):505–523.
-valued extension of the fractional maximal operators for non-doubling measures via potential operators. International Journal of Pure and Applied Mathematics 2006,26(4):505–523.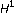 , and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432
, and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432