- Research Article
- Open access
- Published:
Weighted estimates for commutators on nonhomogeneous spaces
Journal of Inequalities and Applications volume 2006, Article number: 89396 (2006)
Abstract
Let be a Borel measure on
be a Borel measure on which may be nondoubling. The only condition that
which may be nondoubling. The only condition that must satisfy is
must satisfy is for any cube
for any cube with sides parallel to the coordinate axes and for some fixed
with sides parallel to the coordinate axes and for some fixed with
with . This paper is to establish the weighted norm inequality for commutators of Calderón-Zygmund operators with
. This paper is to establish the weighted norm inequality for commutators of Calderón-Zygmund operators with functions by an estimate for a variant of the sharp maximal function in the context of the nonhomogeneous spaces.
functions by an estimate for a variant of the sharp maximal function in the context of the nonhomogeneous spaces.
References
Chen W, Sawyer E: A note on commutators of fractional integrals with
 functions. Illinois Journal of Mathematics 2002,46(4):1287–1298.
functions. Illinois Journal of Mathematics 2002,46(4):1287–1298.García-Cuerva J, Martell JM: Weighted inequalities and vector-valued Calderón-Zygmund operators on non-homogeneous spaces. Publicacions Matemàtiques 2000,44(2):613–640.
García-Cuerva J, Martell JM: On the existence of principal values for the Cauchy integral on weighted Lebesgue spaces for non-doubling measures. The Journal of Fourier Analysis and Applications 2001,7(5):469–487. 10.1007/BF02511221
García-Cuerva J, Martell JM: Two-weight norm inequalities for maximal operators and fractional integrals on non-homogeneous spaces. Indiana University Mathematics Journal 2001,50(3):1241–1280.
Han YC: Weighted estimates for higher-order commutators of singular integral operators on non-homogeneous spaces. Journal of South China Normal University. Natural Science Edition 2005,2005(3):92–99.
Komori Y: Weighted estimates for operators generated by maximal functions on nonhomogeneous spaces. Georgian Mathematical Journal 2005,12(1):121–130.
Mateu J, Mattila P, Nicolau A, Orobitg J: BMO for nondoubling measures. Duke Mathematical Journal 2000,102(3):533–565. 10.1215/S0012-7094-00-10238-4
Nazarov F, Treil S, Volberg A: Cauchy integral and Calderón-Zygmund operators on nonhomogeneous spaces. International Mathematics Research Notices 1997,1997(15):703–726. 10.1155/S1073792897000469
Nazarov F, Treil S, Volberg A: Weak type estimates and Cotlar inequalities for Calderón-Zygmund operators on nonhomogeneous spaces. International Mathematics Research Notices 1998,1998(9):463–487. 10.1155/S1073792898000312
Nazarov F, Treil S, Volberg A: Accretive system
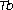 -theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4
-theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4Orobitg J, Pérez C:
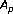 weights for nondoubling measures inand applications
weights for nondoubling measures inand applications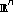 . Transactions of the American Mathematical Society 2002,354(5):2013–2033. 10.1090/S0002-9947-02-02922-7
. Transactions of the American Mathematical Society 2002,354(5):2013–2033. 10.1090/S0002-9947-02-02922-7Pérez C: Endpoint estimates for commutators of singular integral operators. Journal of Functional Analysis 1995,128(1):163–185. 10.1006/jfan.1995.1027
Tolsa X: Cotlar's inequality without the doubling condition and existence of principal values for the Cauchy integral of measures. Journal für die reine und angewandte Mathematik 1998, 502: 199–235.
Tolsa X:
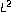 -boundedness of the Cauchy integral operator for continuous measures. Duke Mathematical Journal 1999,98(2):269–304. 10.1215/S0012-7094-99-09808-3
-boundedness of the Cauchy integral operator for continuous measures. Duke Mathematical Journal 1999,98(2):269–304. 10.1215/S0012-7094-99-09808-3Tolsa X: BMO,
 , and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432
, and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432Tolsa X: Littlewood-Paley theory and the
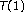 theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011
theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011Tolsa X: The space
 for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8
for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8Verdera J: The fall of the doubling condition in Calderón-Zygmund theory. Publicacions Matemàtiques 2002, 2002: Vol. Extra, 275–292.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, W., Zhao, B. Weighted estimates for commutators on nonhomogeneous spaces. J Inequal Appl 2006, 89396 (2006). https://doi.org/10.1155/JIA/2006/89396
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/89396
 functions. Illinois Journal of Mathematics 2002,46(4):1287–1298.
functions. Illinois Journal of Mathematics 2002,46(4):1287–1298.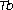 -theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4
-theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4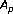 weights for nondoubling measures inand applications
weights for nondoubling measures inand applications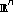 . Transactions of the American Mathematical Society 2002,354(5):2013–2033. 10.1090/S0002-9947-02-02922-7
. Transactions of the American Mathematical Society 2002,354(5):2013–2033. 10.1090/S0002-9947-02-02922-7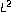 -boundedness of the Cauchy integral operator for continuous measures. Duke Mathematical Journal 1999,98(2):269–304. 10.1215/S0012-7094-99-09808-3
-boundedness of the Cauchy integral operator for continuous measures. Duke Mathematical Journal 1999,98(2):269–304. 10.1215/S0012-7094-99-09808-3 , and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432
, and Calderón-Zygmund operators for non doubling measures. Mathematische Annalen 2001,319(1):89–149. 10.1007/PL00004432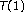 theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011
theorem with non-doubling measures. Advances in Mathematics 2001,164(1):57–116. 10.1006/aima.2001.2011 for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8
for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8