- Research Article
- Open access
- Published:
Global integrability of the Jacobian of a composite mapping
Journal of Inequalities and Applications volume 2006, Article number: 89134 (2006)
Abstract
We first obtain an improved version of the Hölder inequality with Orlicz norms. Then, as an application of the new version of the Hölder inequality, we study the integrability of the Jacobian of a composite mapping. Finally, we prove a norm comparison theorem.
References
Brezis H, Fusco N, Sbordone C: Integrability for the Jacobian of orientation preserving mappings. Journal of Functional Analysis 1993,115(2):425–431. 10.1006/jfan.1993.1098
Gehring FW: The-integrability of the partial derivatives of a quasiconformal mapping. Acta Mathematica 1973, 130: 265–277. 10.1007/BF02392268
Hogan J, Li C, McIntosh A, Zhang K: Global higher integrability of Jacobians on bounded domains. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2000,17(2):193–217.
Iwaniec T, Sbordone C: On the integrability of the Jacobian under minimal hypotheses. Archive for Rational Mechanics and Analysis 1992,119(2):129–143. 10.1007/BF00375119
Iwaniec T, Sbordone C: Weak minima of variational integrals. Journal für die reine und angewandte Mathematik 1994, 454: 143–161.
Iwaniec T, Verde A: On the operator
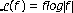 Journal of Functional Analysis 1999,169(2):391–420. 10.1006/jfan.1999.3443
Journal of Functional Analysis 1999,169(2):391–420. 10.1006/jfan.1999.3443Müller S: Higher integrability of determinants and weak convergence in. Journal für die reine und angewandte Mathematik 1990, 412: 20–34.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ding, S., Liu, B. Global integrability of the Jacobian of a composite mapping. J Inequal Appl 2006, 89134 (2006). https://doi.org/10.1155/JIA/2006/89134
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/89134
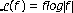 Journal of Functional Analysis 1999,169(2):391–420. 10.1006/jfan.1999.3443
Journal of Functional Analysis 1999,169(2):391–420. 10.1006/jfan.1999.3443