Skip to main content
Journal of Inequalities and Applications
Download PDF

Dual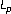 affine isoperimetric inequalities

Journal of Inequalities and Applications volume 2006, Article number: 84825 (2006) Cite this article

Abstract

We establish some inequalities for the dual-centroid bodies which are the dual forms of the results by Lutwak, Yang, and Zhang. Further, we establish a Brunn-Minkowski-type inequality for the polar of dual-centroid bodies.

[12345678910]

References

  1. Campi S, Gronchi P: The-Busemann-Petty centroid inequality. Advances in Mathematics 2002,167(1):128–141. 10.1006/aima.2001.2036

    MATH  MathSciNet  Article  Google Scholar 

  2. Firey WmJ: -means of convex bodies. Mathematica Scandinavica 1962, 10: 17–24.

    MATH  MathSciNet  Google Scholar 

  3. Gardner RJ: Geometric Tomography, Encyclopedia of Mathematics and Its Applications. Volume 58. Cambridge University Press, Cambridge; 1995:xvi+424.

    Google Scholar 

  4. Lutwak E: The Brunn-Minkowski-Firey theory. I. Mixed volumes and the Minkowski problem. Journal of Differential Geometry 1993,38(1):131–150.

    MATH  MathSciNet  Google Scholar 

  5. Lutwak E, Yang D, Zhang G: affine isoperimetric inequalities. Journal of Differential Geometry 2000,56(1):111–132.

    MATH  MathSciNet  Google Scholar 

  6. Lutwak E, Yang D, Zhang G: A new ellipsoid associated with convex bodies. Duke Mathematical Journal 2000,104(3):375–390. 10.1215/S0012-7094-00-10432-2

    MATH  MathSciNet  Article  Google Scholar 

  7. Lutwak E, Yang D, Zhang G: John ellipsoids. Proceedings of the London Mathematical Society. Third Series 2005,90(2):497–520. 10.1112/S0024611504014996

    MATH  MathSciNet  Article  Google Scholar 

  8. Lutwak E, Zhang G: Blaschke-Santaló inequalities. Journal of Differential Geometry 1997,47(1):1–16.

    MATH  MathSciNet  Google Scholar 

  9. Schneider R: Convex Bodies: The Brunn-Minkowski Theory, Encyclopedia of Mathematics and Its Applications. Volume 44. Cambridge University Press, Cambridge; 1993:xiv+490.

    Google Scholar 

  10. Thompson AC: Minkowski Geometry, Encyclopedia of Mathematics and Its Applications. Volume 63. Cambridge University Press, Cambridge; 1996:xvi+346.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science, Beijing Forestry University, Beijing, 100083, China

    Si Lin

  2. Department of Mathematics, East China Normal University, Shanghai, 200062, China

    Xiong Bin

  3. Department of Mathematics, Shanghai University, Shanghai, 200444, China

    Yu Wuyang

Authors
  1. Si Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiong Bin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu Wuyang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Si Lin.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and Permissions

About this article

Cite this article

Lin, S., Bin, X. & Wuyang, Y. Dual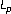 affine isoperimetric inequalities. J Inequal Appl 2006, 84825 (2006). https://doi.org/10.1155/JIA/2006/84825

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/JIA/2006/84825

Keywords

  • Isoperimetric Inequality
  • Dual Form
  • Centroid Body
  • Affine Isoperimetric Inequality