Skip to main content
Journal of Inequalities and Applications
Download PDF
  • Research Article
  • Open access
  • Published:

The Fuglede-Putnam theorem for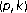-quasihyponormal operators

Journal of Inequalities and Applications volume 2006, Article number: 47481 (2006) Cite this article

Abstract

We show that if is a-quasihyponormal operator and is a-hyponormal operator, and if, where is a quasiaffinity (i.e., a one-one map having dense range), then is a normal and moreover is unitarily equivalent to.

[12345678910111213]

References

  1. Aluthge A: On-hyponormal operators for. Integral Equations and Operator Theory 1990,13(3):307–315. 10.1007/BF01199886

    Article  MATH  MathSciNet  Google Scholar 

  2. Arora SC, Arora P: On-quasihyponormal operators for. Yokohama Mathematical Journal 1993,41(1):25–29.

    MATH  MathSciNet  Google Scholar 

  3. Campbell SL, Gupta BC: On-quasihyponormal operators. Mathematica Japonica 1978/1979,23(2):185–189.

    MathSciNet  MATH  Google Scholar 

  4. Chō M, Itoh M: Putnam's inequality for-hyponormal operators. Proceedings of the American Mathematical Society 1995,123(8):2435–2440.

    MATH  MathSciNet  Google Scholar 

  5. Duggal BP: On-quasihyponormal operators for. Yokohama Mathematical Journal 1993, 41: 25–29.

    MathSciNet  Google Scholar 

  6. Gupta BC, Ramanujan PB: On-quasihyponormal operators II. The Tohoku Mathematical Journal 1968, 20: 417–424. 10.2748/tmj/1178243070

    Article  MATH  Google Scholar 

  7. Jeon IH, Duggal BP: -hyponormal operators and quasisimilarity. Integral Equations and Operator Theory 2004,49(3):397–403. 10.1007/s00020-002-1210-z

    Article  MATH  MathSciNet  Google Scholar 

  8. Kim IH: On-quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.

    Article  MATH  MathSciNet  Google Scholar 

  9. Sheth IH: On hyponormal operators. Proceedings of the American Mathematical Society 1966, 17: 998–1000. 10.1090/S0002-9939-1966-0196498-7

    Article  MATH  MathSciNet  Google Scholar 

  10. Stampfli JG, Wadhwa BL: An asymmetric Putnam-Fuglede theorem for dominant operators. Indiana University Mathematics Journal 1976,25(4):359–365. 10.1512/iumj.1976.25.25031

    Article  MATH  MathSciNet  Google Scholar 

  11. Tanahashi K, Uchiyama A, Chō M: Isolated points of spectrum of-quasihyponormal operators. Linear Algebra and its Applications 2004, 382: 221–229.

    Article  MATH  MathSciNet  Google Scholar 

  12. Uchiyama A: An example of a-quasihyponormal operato. Yokohama Mathematical Journal 1999,46(2):179–180.

    MATH  MathSciNet  Google Scholar 

  13. Williams JP: Operators similar to their adjoints. Proceedings of the American Mathematical Society 1969, 20: 121–123. 10.1090/S0002-9939-1969-0233230-5

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Seoul National University, Seoul, 151-747, Korea

    In Hyoun Kim

Authors
  1. In Hyoun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to In Hyoun Kim.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Kim, I.H. The Fuglede-Putnam theorem for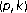-quasihyponormal operators. J Inequal Appl 2006, 47481 (2006). https://doi.org/10.1155/JIA/2006/47481

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/JIA/2006/47481

Keywords