Skip to main content
Journal of Inequalities and Applications
Download PDF
  • Research Article
  • Open access
  • Published:

Riemann-Stieltjes operators from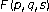 spaces to-Bloch spaces on the unit ball

Journal of Inequalities and Applications volume 2006, Article number: 27874 (2006) Cite this article

Abstract

Let denote the space of all holomorphic functions on the unit ball. We investigate the following integral operators:,,,, where, and is the radial derivative of. The operator can be considered as an extension of the Cesàro operator on the unit disk. The boundedness of two classes of Riemann-Stieltjes operators from general function space, which includes Hardy space, Bergman space, space, BMOA space, and Bloch space, to-Bloch space in the unit ball is discussed in this paper.

[123456789101112131415161718192021]

References

  1. Aleman A, Cima JA: An integral operator onand Hardy's inequality. Journal d'Analyse Mathématique 2001, 85: 157–176.

    Article  MATH  MathSciNet  Google Scholar 

  2. Aleman A, Siskakis AG: An integral operator on. Complex Variables. Theory and Application 1995,28(2):149–158. 10.1080/17476939508814844

    Article  MATH  MathSciNet  Google Scholar 

  3. Aleman A, Siskakis AG: Integration operators on Bergman spaces. Indiana University Mathematics Journal 1997,46(2):337–356.

    Article  MATH  MathSciNet  Google Scholar 

  4. Hardy GH, Littlewood JE: Some properties of fractional integrals. II. Mathematische Zeitschrift 1932,34(1):403–439. 10.1007/BF01180596

    Article  MathSciNet  MATH  Google Scholar 

  5. Hu ZJ: Extended Cesàro operators on mixed norm spaces. Proceedings of the American Mathematical Society 2003,131(7):2171–2179. 10.1090/S0002-9939-02-06777-1

    Article  MATH  MathSciNet  Google Scholar 

  6. Hu ZJ: Extended Cesáro operators on the Bloch space in the unit ball of. Acta Mathematica Scientia. Series B. English Edition 2003,23(4):561–566.

    MATH  MathSciNet  Google Scholar 

  7. Hu ZJ: Extended Cesàro operators on Bergman spaces. Journal of Mathematical Analysis and Applications 2004,296(2):435–454. 10.1016/j.jmaa.2004.01.045

    Article  MATH  MathSciNet  Google Scholar 

  8. Miao J: The Cesàro operator is bounded onfor. Proceedings of the American Mathematical Society 1992,116(4):1077–1079.

    MATH  MathSciNet  Google Scholar 

  9. Ouyang C, Yang W, Zhao R: Möbius invariantspaces associated with the Green's function on the unit ball of. Pacific Journal of Mathematics 1998,182(1):69–99. 10.2140/pjm.1998.182.69

    Article  MathSciNet  MATH  Google Scholar 

  10. Pommerenke C: Schlichte Funktionen und analytische Funktionen von beschränkter mittlerer Oszillation. Commentarii Mathematici Helvetici 1977,52(4):591–602.

    Article  MATH  MathSciNet  Google Scholar 

  11. Shi J-H, Ren G-B: Boundedness of the Cesàro operator on mixed norm spaces. Proceedings of the American Mathematical Society 1998,126(12):3553–3560. 10.1090/S0002-9939-98-04514-6

    Article  MATH  MathSciNet  Google Scholar 

  12. Siskakis AG: Composition semigroups and the Cesàro operator on. Journal of the London Mathematical Society. Second Series 1987,36(1):153–164. 10.1112/jlms/s2-36.1.153

    Article  MATH  MathSciNet  Google Scholar 

  13. Siskakis AG: The Cesàro operator is bounded on. Proceedings of the American Mathematical Society 1990,110(2):461–462.

    MATH  MathSciNet  Google Scholar 

  14. Siskakis AG, Zhao R: A Volterra type operator on spaces of analytic functions. In Function Spaces (Edwardsville, IL, 1998), Contemp. Math.. Volume 232. American Mathematical Society, Rhode Island; 1999:299–311.

    Google Scholar 

  15. Stević S: On an integral operator on the unit ball in. Journal of Inequalities and Applications 2005,2005(1):81–88. 10.1155/JIA.2005.81

    MATH  MathSciNet  Google Scholar 

  16. Xiao J: Cesàro-type operators on Hardy, BMOA and Bloch spaces. Archiv der Mathematik 1997,68(5):398–406. 10.1007/s000130050072

    Article  MATH  MathSciNet  Google Scholar 

  17. Xiao J: Riemann-Stieltjes operators on weighted Bloch and Bergman spaces of the unit ball. Journal of the London Mathematical Society. Second Series 2004,70(1):199–214. 10.1112/S0024610704005484

    Article  MATH  MathSciNet  Google Scholar 

  18. Yoneda R: Pointwise multipliers fromto. Complex Variables. Theory and Application 2004,49(14):1045–1061.

    Article  MATH  MathSciNet  Google Scholar 

  19. Zhang XJ: Multipliers on some holomorphic function spaces. Chinese Annals of Mathematics. Series A 2005,26(4):477–486.

    MATH  MathSciNet  Google Scholar 

  20. Zhao R: On a general family of function spaces. Annales Academiae Scientiarum Fennicae. Mathematica. Dissertationes 1996, (105):56.

  21. Zhu K: Spaces of Holomorphic Functions in the Unit Ball, Graduate Texts in Mathematics. Volume 226. Springer, New York; 2005:x+271.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, JiaYing University, Meizhou, GuangDong, 514015, China

    Songxiao Li

  2. Department of Mathematics, Shantou University, Shantou, GuangDong, 515063, China

    Songxiao Li

Authors
  1. Songxiao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Songxiao Li.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Li, S. Riemann-Stieltjes operators from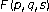 spaces to-Bloch spaces on the unit ball. J Inequal Appl 2006, 27874 (2006). https://doi.org/10.1155/JIA/2006/27874

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/JIA/2006/27874

Keywords